Numerical Hydrodynamics in General Relativity

Abstract

The current status of numerical solutions for the equations of ideal general relativistic hydrodynamics is reviewed. Different formulations of the equations are presented, with special mention of conservative and hyperbolic formulations well-adapted to advanced numerical methods. A representative sample of available numerical schemes is discussed and particular emphasis is paid to solution procedures based on schemes exploiting the characteristic structure of the equations through linearized Riemann solvers. A comprehensive summary of relevant astrophysical simulations in strong gravitational fields, including gravitational collapse, accretion onto black holes and evolution of neutron stars, is also presented.

1 Introduction

The description of important areas of modern astronomy, such as high-energy astrophysics or gravitational wave astronomy, requires General Relativity. High energy radiation is often emitted by highly relativistic events in regions of strong gravitational fields near compact objects such as neutron stars or black holes. The production of relativistic radio jets in active galactic nuclei, explained by pure hydrodynamical effects as in the twin-exhaust model [30], or by magneto-centrifugal acceleration, as in the Blandford-Znajek mechanism [33], involve an accretion disk around a rotating supermassive black hole. The discovery of kHz quasi-periodic oscillations in low-mass X-ray binaries has extended the frequency range over which these oscillations occur into timescales associated with the innermost regions of accretion disks (see, e.g. [219]). Scenarios involving explosive collapse of very massive stars (≈ 30M_⊙) to a black hole (the so-called collapsar and hypernova models), or coalescing compact binaries containing two neutron stars or a neutron star and a black hole, have been proposed as possible candidates to power γ-ray bursts [166, 155, 235, 167]. In addition, coalescing neutron star binaries are among the strongest emitters of gravitational radiation and they constitute one of the main targets for the new generation of gravitational wave detectors going online worldwide in the next few years [218].

A powerful way to improve our understanding of such events is through accurate, large scale, three-dimensional numerical simulations. In the most general case, the equations governing the dynamics of those systems are an intricate, coupled system of time-dependent partial differential equations, comprising the (general) relativistic (magneto-) hydrodynamic equations and the Einstein gravitational field equations. In many cases, the number of equations must be augmented to account for non-adiabatic processes, e.g. radiative transfer or sophisticated microphysics (realistic equations of state for nuclear matter, nuclear physics, magnetic fields, etc.).

Nevertheless, in some astrophysical situations of interest, e.g. accretion of matter onto compact objects, the ‘test-fluid’ approximation is commonly adopted and suffices to get an accurate description. In this approximation the fluid self-gravity is neglected in comparison to the background gravitational field, the core assumption being that the mass μ of the accreting fluid is much smaller than the mass of the compact object M, i.e. μ << M. For instance, a black hole accreting matter at the Eddington rate M_Edd = L_Edd/c² = 1.4 × 10¹⁷ M/M_⊙ g s^-1 would need about 10⁸ years to double its mass, which certainly justifies the assumption. Additionally, a description employing ideal hydrodynamics (i.e. with the stress-energy tensor being that of a perfect fluid), is also a fairly standard choice in numerical astrophysics.

It is the main aim of this review to summarize the existing efforts to solve the equations of (ideal) general relativistic hydrodynamics by numerical means. For this purpose, the most relevant numerical schemes will be presented in some detail. Furthermore, relevant applications in a number of different astrophysical systems, including gravitational collapse, accretion onto compact objects and hydrodynamical evolution of neutron stars, will also be summarized here.

Numerical simulations of strong-field scenarios employing Newtonian gravity and hydrodynamics, as well as possible post-Newtonian extensions, which have received considerable attention in the literature, will not be covered, since this review focuses on relativistic simulations. Nevertheless, we must emphasize that most of what is known about hydrodynamics near compact objects, in particular in black hole astrophysics, has been accurately described using Newtonian models. Probably the best known example is the use of a pseudo-Newtonian potential for non-rotating black holes which mimics the existence of an event horizon at the Schwarzschild gravitational radius [168], which has allowed accurate interpretations of observational phenomena.

The organization of this paper is as follows: Section 2 presents the equations of general relativistic hydrodynamics, summarizing the most relevant theoretical formulations which, to some extent, have helped to drive the development of numerical algorithms for their solution. Section 3 is mainly devoted to describing numerical schemes specifically designed for non-linear hyperbolic systems. Hence, particular emphasis will be paid on conservative high-resolution shock-capturing methods based on linearized Riemann solvers. Also alternative schemes such as smoothed particle hydrodynamics (SPH) and (pseudo-) spectral methods will be briefly discussed. Section 4 summarizes a comprehensive sample of hydrodynamical simulations in strong-field general relativistic astrophysics.

Geometrized units (G = c = 1) are used throughout the paper except where explicitly indicated, as well as the metric conventions of [14]. Greek (Latin) indices run from 0 to 3 (1 to 3).

2 Equations of General Relativistic Hydrodynamics

The general relativistic hydrodynamic equations consist of the local conservation laws of the stress-energy tensor, T^μν (the Bianchi identities) and of the matter current density, J^μ (the continuity equation):

$${\nabla _\mu }{T^{\mu \nu }} = 0,$$

((1))

$${\nabla _\mu }{J^\mu } = 0.$$

((2))

As usual ∇_μ stands for the covariant derivative associated with the four-dimensional spacetime metric g_μν. The density current is given by J^μ = ρu^μ, u^μ representing the fluid 4-velocity and ρ the rest-mass density in a locally inertial reference frame.

The stress-energy tensor for a non-perfect fluid is defined as

$${T^{\mu \nu }} = \rho (1 + \varepsilon ){u^\mu }{u^\nu } + (p - \zeta \theta ){h^{\mu \nu }} - 2\eta {\sigma ^{\mu \nu }} + {q^\mu }{u^\nu } + {q^\nu }{u^\mu },$$

((3))

where ε is the rest frame specific internal energy density of the fluid, p is the pressure and h^μν is the spatial projection tensor h^μν = u^μu^ν + g^μν. In addition, η and ζ are the shear and bulk viscosities. The expansion θ, describing the divergence or convergence of the fluid world lines is defined as θ = ∇_μu^μ. The symmetric, trace-free, and spatial shear tensor σ^μν, is defined by

$${\sigma ^{\mu \nu }} = \frac{1}{2}({\nabla _\alpha }{u^\mu }{h^{\alpha \nu }} + {\nabla _\alpha }{u^\nu }{h^{\alpha \mu }}) - \frac{1}{3}\theta {h^{\mu \nu }},$$

((4))

and, finally, q^μ is the energy flux vector.

In the following we will neglect non-adiabatic effects, such as viscosity or heat transfer, assuming the stress-energy tensor to be that of a perfect fluid,

$${T^{\mu \nu }} = \rho h{u^\mu }{u^\nu } + p{g^{\mu \nu }},$$

((5))

where we have introduced the relativistic specific enthalpy, h, defined by

$$h = 1 + \varepsilon + \frac{p}{\rho }.$$

((6))

Introducing an explicit coordinate chart (x⁰, xⁱ) the previous conservation equations read

$$\frac{\partial }{{\partial {x^\mu }}}\sqrt { - g} {J^\mu } = 0,$$

((7))

$$\frac{\partial }{{\partial {x^\mu }}}\sqrt { - g} {T^{\mu \nu }} = - \sqrt { - g} \Gamma _{\mu \lambda }^\nu {T^{\mu \lambda }},$$

((8))

where the scalar x⁰ represents a foliation of the spacetime with hypersurfaces (coordinatized by xⁱ). Additionally, $\sqrt { - g}$ is the volume element associated with the 4-metric, with g = det(g_μν), and Γ ^ν _μλ are the 4-dimensional Christoffel symbols.

The system formed by the equations of motion (1) and the continuity equation (2) must be supplemented with an equation of state (EOS) relating some fundamental thermodynamical quantities. In general, the EOS takes the form

$$p = p(\rho ,\:\varepsilon ).$$

((9))

In the ‘test-fluid’ approximation, where the fluid self-gravity is neglected, the dynamics of the system is completely governed by Eqs. (1) and (2), together with the EOS (9). In those situations where such approximation does not hold, the previous equations must be solved in conjunction with the Einstein gravitational field equations,

$${G^{\mu \nu }} = 8\pi {T^{\mu \nu }},$$

((10))

which describe the evolution of a dynamical spacetime. The formulation of the Einstein equations as an initial value (Cauchy) problem, in the presence of matter fields, adopting the so-called 3+1 decomposition of the spacetime [15] can be found in, e.g., [240]. Given a choice of gauge, the Einstein equations in the 3+1 formalism [15] split into evolution equations for the 3-metric γ_ij and the extrinsic curvature K_ij, and constraint equations, the Hamiltonian and momentum constraints, that must be satisfied at every time slice. Alternatively, a characteristic initial value problem formulation of the Einstein equations was developed by Bondi, van der Burg and Metzner [41], and Sachs [188]. A recent review of the characteristic formulation is presented in a Living Reviews article by Winicour [233].

Traditionally, most of the approaches for numerical integrations of the general relativistic hydrodynamic equations have adopted spacelike foliations of the spacetime, within the 3+1 formulation. Recently, however, covariant forms of these equations, well suited for advanced numerical methods, have also been developed. This is reviewed next in a chronological way.

2.1 Spacelike (3+1) approaches

In the 3+1 (ADM) formulation [15], spacetime is foliated into a set of non-intersecting spacelike hypersurfaces. There are two kinematic variables describing the evolution between these surfaces: the lapse function α, which describes the rate of advance of time along a timelike unit vector n^μ normal to a surface, and the spacelike shift vector βⁱ that describes the motion of coordinates within a surface.

The line element is written as

$$d{s^2} = - ({\alpha ^2} - {\beta _i}{\beta ^i})d{x^0}d{x^0} + 2{\beta _i}d{x^i}d{x^0} + {\gamma _{ij}}d{x^i}d{x^j},$$

((11))

where γ_ij is the 3-metric induced on each spacelike slice.

2.1.1 May and White

The pioneering numerical work in general relativistic hydrodynamics dates back to the one-dimensional gravitational collapse code of May and White [133, 134]. Building on theoretical work by Misner and Sharp [143], May and White developed a numerical code to solve the evolution equations describing adiabatic spherical collapse in general relativity. This code was based on a Lagrangian finite difference scheme, in which the coordinates are co-moving with the fluid. Artificial viscosity terms were included in the equations to damp the spurious numerical oscillations caused by the presence of shock waves in the flow solution. May and White’s formulation became the starting point of a large number of numerical investigations in subsequent years and, hence, it is worth describing its main features in some detail.

For a spherically symmetric spacetime the line element can be written as

$$d{s^2} = - {a^2}(m,\:t)d{t^2} + {b^2}(m,\:t)d{m^2} + {R^2}(m,\:t)(d{\theta ^2} + {\sin ^2}\theta d{\phi ^2}),$$

((12))

m being a radial (Lagrangian) coordinate, indicating the total rest-mass enclosed inside the circumference 2πR(m, t).

The co-moving character of the coordinates leads, for a perfect fluid, to a stress-energy tensor of the form

$$T_1^1\: = \:T_2^2 = T_3^3 = - p,$$

((13))

$$T_0^0\: = \:(1 + \varepsilon )\rho ,$$

((14))

$$T_\nu ^\mu = 0\;\;\;\;\;{\mathrm{if}}\;\mu \ne \nu .$$

((15))

In these coordinates the local conservation equation for the baryonic mass, Eq. (2), can be easily integrated:

$$b = \frac{1}{{4\pi \rho {R^2}}}.$$

((16))

The gravitational field equations, Eq. (10), and the equations of motion, Eq. (1), reduce to the following quasi-linear system of partial differential equations (see also [143]):

$$\frac{{\partial p}}{{\partial m}} + \frac{1}{a}\frac{{\partial a}}{{\partial m}}\rho h = 0,$$

((17))

$$\frac{{\partial \varepsilon }}{{\partial t}} + p\frac{\partial }{{\partial t}}\left( {\frac{1}{\rho }} \right) = 0,$$

((18))

$$\frac{{\partial u}}{{\partial t}} = - a\left( {4\pi \frac{{\partial p}}{{\partial m}}{R^2}\frac{\Gamma }{h} + \frac{M}{{{R^2}}} + 4\pi pR} \right),$$

((19))

$$\frac{1}{{\rho {R^2}}}\frac{{\partial \rho {R^2}}}{{\partial t}} = - a\frac{{\partial u/\partial m}}{{\partial R/\partial m}},$$

((20))

with the definitions

$$u = \frac{1}{a}\frac{{\partial R}}{{\partial t}},\:\Gamma = \frac{1}{b}\frac{{\partial R}}{{\partial m}},$$

((21))

satisfying

$${\Gamma ^2} = 1 - {u^2} - \frac{{2M}}{R}.$$

((22))

Additionally,

$$M = \int_0^m {4\pi {R^2}\rho (1 + \varepsilon )\frac{{\partial R}}{{\partial m}}dm} $$

((23))

represents the total mass interior to radius m at time t. The final system is closed with an EOS of the form (9).

Codes based on the original formulation of May and White and on later versions (e.g. [222]) have been used in many non-linear simulations of supernova and neutron star collapse (see, e.g., [142, 215] and references therein), as well as in perturbative computations of spherically symmetric gravitational collapse employing the linearized Einstein theory [192, 194, 193]. In Section 4.1.1 some of these simulations are reviewed in detail. The Lagrangian character of May and White’s code, together with other theoretical considerations concerning the particular coordinate gauge, has prevented its extension to multidimensional calculations. However, for one-dimensional problems, the Lagrangian approach adopted by May and White has considerable advantages with respect to an Eulerian approach with spatially fixed coordinates, mainly the lack of numerical diffusion.

2.1.2 Wilson

The use of Eulerian coordinates in multidimensional numerical relativistic hydrodynamics started with the pioneering work by Wilson [227]. Introducing the basic dynamical variables D, S_μ, and E, representing the relativistic density, momenta, and energy, respectively, defined as

$$D = \rho {u^0},\:\;\;\;\;\;{S_\mu } = \rho h{u_\mu }{u^0},\:\;\;\;\;\;E = \rho \varepsilon {u^0},$$

((24))

the equations of motion in Wilson’s formulation [227, 228] are:

$$\frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^0}}}(D\sqrt { - g} ) + \frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^i}}}(D{V^i}\sqrt { - g} ) = 0,$$

((25))

$$\frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^0}}}({S_\mu }\sqrt { - g} ) + \frac{1}{{\sqrt { - g} }}\frac{\partial }{{\partial {x^i}}}({S_\mu }{V^i}\sqrt { - g} ) + \frac{{\partial p}}{{\partial {x^\mu }}} + \frac{1}{2}\frac{{\partial {g^{\alpha \beta }}}}{{\partial {x^\mu }}}\frac{{{S_\alpha }{S_\beta }}}{{{S^0}}} = 0,$$

((26))

$$\frac{\partial }{{\partial {x^0}}}(E\sqrt { - g} ) + \frac{\partial }{{\partial {x^i}}}(E{V^i}\sqrt { - g} ) + p\frac{\partial }{{\partial {x^\mu }}}({u^0}{V^\mu }\sqrt { - g} ) = 0,$$

((27))

with the “transport velocity” given by V^μ = u^μ/u⁰. Notice that the momentum density equation, Eq. (26), is only solved for the three spatial components, S_i, and S₀ is obtained through the 4-velocity normalization condition u_μu^μ = -1.

A direct inspection of the system shows that the equations are written as a coupled set of advection equations. In doing so, the terms containing derivatives (in space or time) of the pressure are treated as source terms. This approach, hence, sidesteps an important guideline for the formulation of non-linear hyperbolic systems of equations, namely the preservation of their conservation form. This is a necessary feature to guarantee correct evolution in regions of sharp entropy generation (i.e. shocks). As a consequence, some amount of numerical dissipation must be used to stabilize the solution across discontinuities. The first attempt to solve the equations of general relativistic hydrodynamics in the original Wilson scheme [227] used a combination of finite difference upwind techniques with artificial viscosity terms. Such terms extended the classic treatment of shocks introduced by von Neumann and Richtmyer [224] into the relativistic regime (see Section 3.1.1).

Wilson’s formulation has been widely used in hydrodynamical codes developed by a variety of research groups. Many different astrophysical scenarios were first investigated with these codes, including axisymmetric stellar core-collapse [150, 149, 153, 19, 212, 178, 66], accretion onto compact objects [95, 176], numerical cosmology [48, 49, 13] and, more recently, the coalescence and merger of neutron star binaries [231, 232]. This formalism has also been extensively employed, in the special relativistic limit, in numerical studies of heavy-ion collisions [230, 136]. We note that in these investigations, the original formulation of the hydrodynamic equations was slightly modified by redefining the dynamical variables, Eq. (24), with the addition of a multiplicative α factor and the introduction of the Lorentz factor, W = αu⁰ (the “relativistic gamma”):

$$D = \rho W,\;\;\;\;\;{S_\mu } = \rho hW{u_\mu },\:\;\;\;\;\;E = \rho \varepsilon W.$$

((28))

As mentioned before, the description of the evolution of self-gravitating matter fields in general relativity requires a joint integration of the hydrodynamic equations and the gravitational field equations (the Einstein equations). Using Wilson’s formulation for the fluid dynamics, this was first considered in [228], building on a vacuum numerical relativity code specifically developed to investigate the head-on collision of two black holes [210]. The resulting code was axially symmetric and aimed to integrate the coupled set of equations in the context of stellar core collapse [68].

More recently, Wilson’s formulation has also been applied to the numerical study of the coalescence of binary neutron stars in general relativity [231, 232] (see Section 4.3). An approximation scheme for the gravitational field has been adopted in these studies, by imposing the simplifying condition that the three-geometry (the three metric) is conformally flat. The line element then reads

$$d{s^2} = - ({\alpha ^2} - {\beta _i}{\beta ^i})d{x^0}d{x^0} + 2{\beta _i}d{x^i}d{x^0} + {\phi ^4}{\delta _{ij}}d{x^i}d{x^j}.$$

((29))

The curvature of the three metric is then described by a position dependent conformal factor ϕ⁴ times a flat-space Kronecker delta. Therefore, in this approximation scheme all radiation degrees of freedom are thrown away, and the field equations reduce to a set of five Poisson-like elliptic equations in flat space-time for the lapse, the shift vector and the conformal factor. While in spherical symmetry this approximation is identical to Einstein’s theory, in more general situations it has the same accuracy as the first post-Newtonian approximation [109].

Wilson’s formulation showed some limitations in handling situations involving ultrarelativistic flows, as first pointed out by Centrella and Wilson [49]. Norman and Winkler [160] performed a comprehensive numerical study of such formulation by means of special relativistic hydrodynamical simulations. Fig. 1 reproduces a plot from [160] in which the relative error of the density compression ratio in the relativistic shock reflection problem — the heating of a cold gas which impacts at relativistic speeds with a solid wall and bounces back — is displayed as a function of the Lorentz factor W of the incoming gas. The source of the data is [49]. This figure shows that for Lorentz factors of about 2 (v ≈ 0.86c), the threshold of the ultrarelativistic limit, the relative errors are between 5% and 7% (depending on the adiabatic exponent of the gas), showing a linear growth with W.

Figure 1

Results for the shock heating test of a cold, relativistically inflowing gas against a wall using the explicit Eulerian techniques of Centrella and Wilson [49]: Dependence of the relative errors of the density compression ratio versus the Lorentz factor W for two different values of the adiabatic index of the flow, Γ = 4/3 (triangles) and Γ = 5/3 (circles) gases. The relative error is measured with respect to the average value of the density over a region in the shocked material. The data are from Centrella and Wilson [49], and the plot reproduces a similar one from Norman and Winkler [160].

Norman and Winkler [160] concluded that those large errors were mainly due to the way in which the artificial viscosity terms are included in the numerical scheme in Wilson’s formulation. These terms, called collectively Q (see Section 3.1.1), are only added to the pressure terms in some cases, namely at the pressure gradient in the source of the momentum equation and at the divergence of the velocity in the source of the energy equation. However, [160] proposed to add the Q terms globally in order to consider the artificial viscosity as a real viscosity. Hence, the hydrodynamic equations should be rewritten for a modified stress-energy tensor of the following form:

$${T^{\mu \nu }} = \rho (1 + \varepsilon + \frac{{p + Q}}{\rho }){u^\mu }{u^\nu } + (p + Q){g^{\mu \nu }}.$$

((30))

In this way, in flat spacetime, the momentum equation takes the form:

$$\frac{\partial }{{\partial {x^0}}}[(\rho h + Q){W^2}{V_j}] + \frac{\partial }{{\partial {x^i}}}[(\rho h + Q){W^2}{V_j}{V^i}] + \frac{{\partial (p + Q)}}{{\partial {x^j}}} = 0.$$

((31))

In Wilson’s formulation Q is omitted in the two terms containing the quantity ρh. In general Q is a non-linear function of the velocity and, hence, the quantity QW²V in the momentum density of Eq. (31) is a highly non-linear function of the velocity and its derivatives. This fact, together with the explicit presence of the Lorentz factor in the convective terms of the hydrodynamic equations, as well as the pressure in the specific enthalpy, make the relativistic equations much more coupled than their Newtonian counterparts. As a result Norman and Winkler proposed the use of implicit schemes to describe more accurately such coupling. Their code, which incorporates an adaptive grid, reproduces very accurate results even for ultrarelativistic flows with Lorentz factors of about 10 in one-dimensional flat spacetime simulations.

2.1.3 Valencia

In 1991 the Valencia group [126] presented a new formulation of the (Eulerian) general relativistic hydrodynamic equations. This formulation was aimed to take fundamental advantage of the hyperbolic and conservative character of the equations. Numerically, the hyperbolic and conservative nature of the relativistic Euler equations allows for the use of schemes based on the characteristic fields of the system, translating existing tools of classical fluid dynamics to relativistic hydrodynamics. This procedure departs from earlier approaches, most notably in avoiding the need for artificial dissipation terms to handle discontinuous solutions [228], as well as implicit schemes as proposed in [160].

A numerical scheme written in conservation form automatically guarantees the correct Rankine-Hugoniot (jump) conditions across discontinuities (the shock-capturing property). Writing the relativistic hydrodynamic equations as a system of conservation laws, identifying the suitable vector of unknowns and building up an approximate Riemann solver permitted the extension of state-of-the-art high-resolution shock-capturing (HRSC in the following) schemes from classical fluid dynamics into the realm of relativity [126].

Theoretical advances on the mathematical character of the relativistic hydrodynamic equations were achieved studying the special relativistic limit. In Minkowski spacetime, the hyperbolic character of relativistic (magneto-) hydrodynamics was exhaustively studied by Anile and collaborators (see [11] and references therein) by applying Friedrichs’ definition of hyperbolicity [79] to a quasi-linear form of the system of hydrodynamic equations,

$$\mathcal{A}^{\mu}(\mathrm{w})\frac{\partial \mathrm{w}}{\partial x^{\mu}}=0,$$

((32))

where ${{\mathcal A}^\mu }$ are the Jacobian matrices of the system and w are a suitable set of primitive variables (see below). System (32) will be hyperbolic in the time-direction defined by the vector field ξ with ξ_μξ^μ = -1, if the following two conditions hold:

• (i) $\det ({{\mathcal A}^\mu }{\xi _\mu }) \ne 0$ and

• (ii) for any ζ such that ζ_μξ^μ = 0, ζ_μζ^μ = 1,

the eigenvalue problem ${{\mathcal A}^\mu }({\zeta _\mu } - \lambda {\xi _\mu }){\mathrm{r}} = 0$ has only real eigenvalues {λ_n}_n=i,…,5, and a complete set of right-eigenvectors {r_n}_n=1,…,5. Besides verifying the hyperbolic character of the relativistic hydrodynamic equations, Anile and collaborators [11] obtained the explicit expressions for the eigenvalues and eigenvectors in the local rest frame, characterized by u^μ = δ ^μ₀ . In Font et al. [73] those calculations were extended to an arbitrary reference frame in which the motion of the fluid was described by the 4-velocity u^μ = W (1, vⁱ).

The extension to general relativity of the approach, followed in [73] for special relativity, was accomplished in [18]. We will refer to the formulation of the general relativistic hydrodynamic equations presented in [18] as the Valencia formulation. The choice of evolved variables (conserved quantities) in this formulation differs slightly from Wilson’s formulation. It comprises the rest-mass density (D), the momentum density in the j-direction (S_j), and the total energy density (E), measured by a family of observers which are the natural extension (for a generic spacetime) of the Eulerian observers in classical fluid dynamics. Interested readers are addressed to [18] for their definition and geometrical foundations.

In terms of the primitive variables w = (ρ, v_i, ε), the conserved quantities are written as:

$$D = \rho W,$$

((33))

$${S_j} = \rho h{W^2}{v_j},$$

((34))

$$E = \rho h{W^2} - p,$$

((35))

where the contravariant components vⁱ = γ^ijv_j of the three-velocity are defined as

$${v^i} = \frac{{{u^i}}}{{\alpha {u^0}}} + \frac{{{\beta ^i}}}{\alpha },$$

((36))

and W is the relativistic Lorentz factor W ≡ αu⁰ = (1 - v²)^-1/2 with v² = γ_ijvⁱv^j.

With this choice of variables the equations can be written in conservation form. Strict conservation is only possible in flat spacetime. For curved space-times there exist source terms, coming from the spacetime geometry, which do not contain derivatives of stress-energy tensor components. More precisely, the first-order flux-conservative hyperbolic system, well suited for numerical applications, reads:

$$\frac{1}{{\sqrt { - g} }}\left( {\frac{{\partial \sqrt \gamma {\mathrm{U}}({\mathrm{w}})}}{{\partial {x^0}}} + \frac{{\partial \sqrt { - g} {{\mathrm{F}}^i}({\mathrm{w}})}}{{\partial {x^i}}}} \right) = {\mathrm{S}}({\mathrm{w}}),$$

((37))

with g = det(g_μv) satisfying $\sqrt { - g} = \alpha \sqrt \gamma$ with γ = det(γ_ij). The state vector is given by

$${\mathrm{U}}({\mathrm{w}}) = (D,\:{S_j},\:\tau ),$$

((38))

with τ = E - D. The vector of fluxes is

$${{\mathrm{F}}^i}({\mathrm{w}}) = \left( {D\left( {{v^i} - \frac{{{\beta ^i}}}{\alpha }} \right),\;{S_j}\left( {{v^i} - \frac{{{\beta ^i}}}{\alpha }} \right) + p\delta _j^i,\;\tau \left( {{v^i} - \frac{{{\beta ^i}}}{\alpha }} \right) + p{v^i}} \right),$$

((39))

and the corresponding sources S(w) are

$${\mathrm{S}}({\mathrm{w}}) = \left( {0,\:\;{T^{\mu \nu }}\left( {\frac{{\partial {g_{\nu j}}}}{{\partial {x^\mu }}} - \Gamma _{\nu \mu }^\delta {g_{\delta j}}} \right),\;\alpha \left( {{T^{\mu 0}}\frac{{\partial \ln \alpha }}{{\partial {x^\mu }}} - {T^{\mu \nu }}\Gamma _{\nu \mu }^0} \right)} \right).$$

((40))

The local characteristic structure of the previous system of equations was presented in [18]. The eigenvalues (characteristic speeds) of the corresponding Jacobian matrices are all real (but not distinct, one showing a threefold degeneracy) and a complete set of right-eigenvectors exists. System (37) satisfies, hence, the definition of hyperbolicity. As discussed in Section 3.1.2 below, the knowledge of the spectral information is essential in order to construct HRSC schemes based on Riemann solvers. This information can be found in [18] (see also [76]).

The range of applications considered so far in general relativity employing this formulation is still small and mostly devoted to the study of accretion flows onto black holes (see Section 4.2.2 below). In the special relativistic limit this formulation is being successfully applied to model the evolution of (ultra-) relativistic extragalactic jets (see, e.g., [130, 10]). The first numerical studies in general relativity were performed, in one spatial dimension, in [126], using a slightly different form of the equations. Preliminary investigations of gravitational stellar collapse were attempted by coupling the Valencia formulation to a hyperbolic formulation of the Einstein equations developed by [35]. Some discussion of these results can be found in [124, 34]. More recently, successful evolutions of fully dynamical spacetimes in the context of adiabatic spherically symmetric stellar core-collapse have been achieved [102, 185]. We will come back to these issues in Section 4.1.1 below.

Recently, a three-dimensional, Eulerian, general relativistic hydrodynamical code, evolving the coupled system of the Einstein and hydrodynamic equations, has been developed [76]. The formulation of the hydrodynamic equations follows the Valencia approach. The code is constructed for a completely general space-time metric based on a Cartesian coordinate system, with arbitrarily specifiable lapse and shift conditions. In [76] the spectral decomposition (eigenvalues and right-eigenvectors) of the general relativistic hydrodynamic equations, valid for general spatial metrics, was derived, correcting earlier results of [18] for non-diagonal metrics. A complete set of left-eigenvectors has been recently presented by Ibáñez et al. [100]. This information is summarized in Section 5.2.

The formulation of the coupled set of equations and the numerical code reported in [76] were used for the construction of the milestone code "GR3D" for the NASA Neutron Star Grand Challenge project. For a description of the project see the website of the Washington University Gravity Group [1]. A public domain version of the code has recently been released to the community at the same website, the source and documentation of this code can be downloaded at [2].

2.2 Covariant approaches

General (covariant) conservative formulations of the general relativistic hydro-dynamic equations for ideal fluids, i.e. not restricted to spacelike foliations, have been derived in [65] and, more recently, in [172, 169]. The form invariance of these approaches with respect to the nature of the spacetime foliation implies that existing work on highly specialized techniques for fluid dynamics (i.e. HRSC schemes) can be adopted straightforwardly. In the next two sections we describe them in some detail.

2.2.1 Eulderink and Mellema

Eulderink and Mellema [63, 65] first derived a covariant formulation of the general relativistic hydrodynamic equations taking special care, as in the Valencia formulation, of the conservative form of the system, with no derivatives of the dependent fluid variables appearing in the source terms. Additionally, this formulation is strongly tailored towards the use of a numerical method based on a generalization of Roe’s approximate Riemann solver for the non-relativistic Euler equations in Cartesian coordinates [184]. Their procedure is specialized for a perfect fluid EOS, p = (Γ - 1)ρε, Γ being the (constant) adiabatic index of the fluid. After the appropriate choice of the state vector variables, the conservation laws, Eqs. (7) and (8), are re-written in flux-conservative form. The flow variables are expressed in terms of a parameter vector ω as

$${{\mathrm{F}}^\alpha } = \left( {\left[ {K - \frac{\Gamma }{{\Gamma - 1}}{\omega ^4}} \right]{\omega ^\alpha },\:{\omega ^\alpha }{\omega ^\beta } + K{\omega ^4}{g^{\alpha \beta }}} \right),$$

((41))

where ω^α ≡ Ku^α, ω⁴ ≡ Kp/(ρh) and ${K^2} \equiv \sqrt { - g} \rho h = - {g_{\alpha \beta }}{\omega ^\alpha }{\omega ^\beta }$. The vector F⁰ represents the state vector (the unknowns), and each vector Fⁱ is the corresponding flux in the coordinate direction xⁱ.

Eulderink and Mellema computed the appropriate “Roe matrix” [184] for the vector (41) and obtained the corresponding spectral decomposition. The characteristic information is used to solve the system numerically using Roe’s generalized approximate Riemann solver. Roe’s linearization can be expressed in terms of the average state ̃ω = (ω_L + ω_R)/(K_L + K_R), where L and R denote the left and right states in a Riemann problem (see Section 3.2). Further technical details can be found in [63, 65].

The performance of this general relativistic Roe solver was tested in a number of one-dimensional problems for which an exact solution is known, including non-relativistic shock tubes, special relativistic shock tubes and spherical accretion of dust and a perfect fluid onto a (static) Schwarzschild black hole. In its special relativistic version it has been used in the study of the confinement properties of relativistic jets [64]. No astrophysical applications in strong-field general relativistic flows have yet been attempted with this formulation.

2.2.2 Papadopoulos and Font

In this formulation [172] the spatial velocity components of the 4-velocity, uⁱ, together with the rest-frame density and internal energy, ρ and ε, provide a unique description of the state of the fluid and are taken as the primitive variables. They constitute a vector in a five dimensional space, w = (ρ, uⁱ, ε). The initial value problem for equations (7) and (8) is defined in terms of another vector in the same fluid state space, namely the conserved variables, U, individually denoted (D, Sⁱ, E):

$$D = {{\mathrm{U}}^0} = {J^0} = \rho {u^0},$$

((42))

$${S^i} = {{\mathrm{U}}^i} = {T^{0i}} = \rho h{u^0}{u^i} + p{g^{0i}},$$

((43))

$$E = {{\mathrm{U}}^4} = {T^{00}} = \rho h{u^0}{u^0} + p{g^{00}}.$$

((44))

Note that these variables slightly differ from previous choices (see, e.g., Eqs. (24), (33), (34), (35) and (41)). With those definitions the equations take the standard conservation law form,

$$\frac{{\partial (\sqrt { - g} {{\mathrm{U}}^A})}}{{\partial {x^0}}} + \frac{{\partial (\sqrt { - g} {{\mathrm{F}}^j})}}{{\partial {x^j}}} = {\mathrm{S}},$$

((45))

with A = (0, i, 4). The flux vectors F^j and the source terms S (which depend only on the metric, its derivatives and the undifferentiated stress energy tensor), are given by

$${{\mathrm{F}}^j} = ({J^j},\:{T^{ji}},\:{T^{j0}}) = (\rho {u^j},\:\rho h{u^i}{u^j} + p{g^{ij}},\:\rho h{u^0}{u^j} + p{g^{0j}}),$$

((46))

$${\rm{S}} = (0,\: - \sqrt { - g} \Gamma _{\mu \lambda }^i{T^{\mu \lambda }},\: - \sqrt { - g} \Gamma _{\mu \lambda }^0{T^{\mu \lambda }}).$$

((47))

The state of the fluid is uniquely described using either vector of variables, i.e. either U or w, and each one can be obtained from the other via the definitions (42, 43, 44) and the use of the normalization condition for the 4-velocity, g_μνu^μu^ν = -1.

The local characteristic structure of these equations has been presented in [172]. The formulation has proved well suited for the numerical implementation of HRSC schemes. A comprehensive numerical study of this approach was also presented in [172], where it was applied to simulate one-dimensional relativistic flows on null spacetime foliations. The demonstrations performed include standard shock tube tests in Minkowski spacetime, perfect fluid accretion onto a Schwarzschild black hole using ingoing null Eddington-Finkelstein coordinates, and dynamical spacetime evolutions of polytropes (i.e. stellar models satisfying the Tolman-Oppenheimer-Volkoff equilibrium equations) sliced along the radial null cones, and accretion of self-gravitating matter onto a central black hole.

Procedures for integrating various forms of the hydrodynamic equations on null hypersurfaces have been presented before in [104] (see [29] for a recent implementation). This approach is geared towards smooth isentropic flows. A Lagrangian method, applicable in spherical symmetry, has been presented by [140]. Recent work in [59] includes a Eulerian non-conservative formulation for general fluids in null hypersurfaces and spherical symmetry, including their matching to a spacelike section.

A technical remark must be included here: In all conservative formulations reviewed in Sections 2.1.3, 2.2.1, 2.2.2, the time-update of the numerical algorithm is applied to the conserved quantities U. After the update the vector of primitive quantities must be reevaluated, as those are needed in the Riemann solver (see Section 3.1.2). The relation between the two sets of variables is not in closed form and, hence, the update of the primitive variables is done using a root-finding procedure, typically a Newton-Raphson algorithm. This feature may lead to accuracy losses in regions of low density and small speeds, apart from being computationally inefficient. Specific details on this issue can be found in [18, 65, 172]. We note that the covariant formulation discussed in this section, when applied to null spacetime foliations, allows for an explicit recovery of the primitive variables, as a consequence of the particular form of the Bondi-Sachs metric. We end by pointing out that the formulation presented in this section has been developed for a perfect fluid EOS. Extensions to account for generic EOS, as well as a comprehensive analysis of general relativistic hydrodynamics in conservation form, have been recently presented in [169].

2.3 Going further

Formulations of the equations of non-ideal hydrodynamics in general relativity are also available in the literature. Here the term “non-ideal” includes effects such as viscosity, magnetic fields and radiative transfer. These non-adiabatic effects can play a major role in some astrophysical systems as e.g. accretion disks.

The equations of viscous hydrodynamics, the Navier-Stokes-Fourier equations, have been formulated in relativity in terms of causal dissipative relativistic fluids (see the Living Reviews article by Müller [148] for a review). These extended fluid theories are numerically still almost unexplored in astrophysical systems. The reason may be the lack of an appropriate formulation well-suited for numerical studies. Peitz and Appl [174] have recently provided a 3+1 coordinate-free representation of different types of dissipative relativistic fluid theories [120, 61, 105], which has the potential of being well adapted to numerical applications.

The inclusion of magnetic fields and the development of formulations for the magneto-hydrodynamic equations, attractive to numerical studies, is still very limited in general relativity. Numerical approaches in special relativity are presented in [111, 221]. 3+1 representations of relativistic magneto-hydrodynamics can be found in [209, 67]. In [238] the transport of energy and angular momentum in magneto-hydrodynamical accretion onto a rotating black hole was studied adopting Wilson’s formulation for the hydrodynamic equations (conveniently modified to account for the magnetic terms), and the magnetic induction equation was solved using the constrained transport method of [67]. Recently [110] have performed the first magneto-hydrodynamical simulation in general relativity of magnetically driven relativistic jets from an accretion disk around a Schwarzschild black hole.

The interaction between matter and radiation fields, present in different levels of complexity in all astrophysical systems, is described by the equations of radiation hydrodynamics. The Newtonian framework is highly developed (see, e.g., [139]; the special relativistic transfer equation is also considered in that reference). General relativistic formulations of radiative transfer in curved spacetimes are considered in, e.g., [182] and [241] (see also references therein).

3 Numerical Schemes

This section describes the numerical schemes, mainly those based on finite differences, specifically designed to solve non-linear hyperbolic systems of conservation laws. As discussed in the previous section, the equations of general relativistic hydrodynamics fall in this category. Although schemes based on artificial viscosity techniques are also considered, the emphasis is given on the so-called high-resolution shock-capturing (HRSC) schemes (or Godunov-type methods), based on (either exact or approximate) solutions of local Riemann problems using the characteristic fields of the equations. Such finite difference schemes (or, in general, finite volume schemes) have been the subject of diverse review articles and textbooks (see, e.g., [118, 119, 101]). For this reason only the most relevant features will be covered here, referring the reader to the appropriate literature for further details. In particular, an excellent introduction on the implementation of HRSC schemes in special relativistic hydrodynamics is presented in the Living Reviews article by Martí and Müller [127]. Alternative techniques to finite differences, such as Smoothed Particle Hydrodynamics and (pseudo-) Spectral Methods, are briefly considered last.

3.1 Finite difference schemes

Any system of equations presented in the previous section can be solved numerically by replacing the partial derivatives by finite differences on a discrete numerical grid, and then advancing the solution in time via some time-marching algorithm. Hence, specification of U on an initial hypersurface, together with a suitable EOS, followed by a recovery of the primitive variables, leads to the computation of the fluxes and source terms. In doing so, the first time derivative of the data is obtained, which then leads to the formal propagation of the solution forward in time, with a time-step constrained by the Courant-Friedrichs-Lewy (CFL) condition.

Finite difference numerical schemes provide solutions of the discretized version of the original system of partial differential equations. Therefore, convergence properties under grid refinement must be enforced on such schemes to ensure that the numerical results are correct (i.e. the global error of the numerical solution has to tend to zero as the cell width tends to zero). For hyperbolic systems of conservation laws, schemes written in conservation form are preferred as they guarantee that the convergence, if it exists, is to one of the weak solutions of the original system of equations (Lax-Wendroff theorem [117]). Such weak solutions are generalized solutions that satisfy the integral form of the conservation system. They are classical solutions (continuous and differentiable) in regions where they are continuous and have a finite number of discontinuities.

Let us consider an initial value problem for a one-dimensional scalar hyperbolic conservation law,

$$\frac{{\partial u}}{{\partial t}} + \frac{{\partial f(u)}}{{\partial x}} = 0,\:\;\;\;\;\;u(x,\:t = 0) = {u_0}(x).$$

((48))

Introducing a discrete numerical grid of space-time points (x_j, tⁿ), an algorithm written in conservation form reads:

$$u_j^{n + 1} = u_j^n - \frac{{\Delta t}}{{\Delta x}}(\hat f(u_{j - r}^n,\:u_{j - r + 1}^n,\: \cdots ,\:u_{j + q}^n) - \hat f(u_{j - r - 1}^n,\:u_{j - r}^n,\: \cdots ,\:u_{j + q - 1}^n)),$$

((49))

where Δt and Δx are the time-step and cell width respectively, ̂f is a consistent numerical flux function (i.e., ̂f(u, u, …, u) = f(u)) and u ⁿ _j is an approximation to the average of u(x, t) within the numerical cell [x_j-1/2, x_j+1/2] (x_j±1/2 = (x_j + x_j ± 1)/2):

$$u_j^n \approx \frac{1}{{\Delta x}}\int_{{x_{j - 1/2}}}^{{x_{j + 1/2}}} {u(x,\:{t^n})dx.} $$

((50))

The class of all weak solutions is too wide in the sense that there is no uniqueness for the initial value problem. The numerical method should guarantee convergence to the physically admissible solution. This is the vanishing-viscosity limit solution, i.e., the solution when η → 0, of the “viscous version” of Eq. (48):

$$\frac{{\partial u}}{{\partial t}} + \frac{{\partial f(u)}}{{\partial x}} = \eta \frac{{{\partial ^2}u}}{{\partial {x^2}}}.$$

((51))

Mathematically, this solution is characterized by the so-called entropy condition (in the language of fluids, the condition that the entropy of any fluid element should increase when running into a discontinuity). The characterization of the entropy-satisfying solutions for scalar equations was given by Oleinik [163]. For hyperbolic systems of conservation laws it was developed by Lax [116].

The Lax-Wendroff theorem [117] cited above does not establish whether the method converges. To guarantee convergence, some form of stability is required, as Lax proposed for linear problems (Lax equivalence theorem; see, e.g., [183]). Along this direction, the notion of total-variation stability has proven very successful although powerful results have only been obtained for scalar conservation laws. The total variation of a solution at t = tⁿ, TV(uⁿ), is defined as

$${\rm{TV}}({u^n})\; = \sum\limits_{j = 0}^{ + \infty } | u_{j + 1}^n - u_j^n|.$$

((52))

A numerical scheme is said to be TV-stable if TV(uⁿ) is bounded for all Δt at any time for each initial data. In the case of non-linear scalar conservation laws it can be proved that for numerical schemes in conservation form with consistent numerical flux functions, TV-stability is a sufficient condition for convergence [118]. Current research has focused on the development of high-resolution numerical schemes in conservation form satisfying the condition of TV-stability, e.g., the total variation diminishing (TVD) schemes. This issue is further discussed in Section 3.1.2. Additionally, an important property that a numerical method must satisfy is to be monotone. A scheme of the form $u_j^{n + 1} = \sum\nolimits_{k = - {l_1}}^{{l_2}} {{b_k}u_{j + k}^n}$, with l₁ and l₂ two non-negative integers, is said to be monotone if all coefficients b_k are positive or zero. It has been shown that, for scalar conservation laws, monotone methods are TVD and satisfy a discrete entropy condition. Therefore, they converge in a non-oscillatory manner to the unique entropy solution. However, monotone methods are at most first order accurate [118].

The hydrodynamic equations constitute a non-linear hyperbolic system and, hence, smooth initial data can give rise to discontinuous data (crossing of characteristics in the case of shocks) in a finite time during the evolution. As a consequence classical finite difference schemes present important deficiencies when dealing with such systems. Typically, first order accurate schemes are too dissipative across discontinuities (excessive smearing), and second order (or higher) schemes produce spurious oscillations near discontinuities which do not disappear as the grid is refined. Standard finite difference schemes have been conveniently modified in two ways to obtain high-order, oscillation-free accurate representations of discontinuous solutions as we discuss next.

3.1.1 Artificial viscosity schemes

High-resolution schemes based on the idea of modifying the equations by introducing some terms providing artificial viscosity to damp the amplitude of spurious oscillations near discontinuities were originally proposed by von Neumann and Richtmyer [224] to solve the (classical) Euler equations. The basic idea is to introduce a purely artificial dissipative mechanism whose form and strength are such that the shock transition is smooth, extending over a small number of intervals Δx of the space variable. In this approach the equations are discretised using a high order finite difference method (e.g., a second order Lax-Wendroff scheme), which gives good results in smooth parts of the flow solution, adding an artificial viscosity term Q to the hyperbolic system which only acts where discontinuities arise. The term Q must vanish as the grid is refined and the time step is reduced, i.e. Δt, Δx → 0.

Von Neumann and Richtmyer derived the following expression for the viscosity term:

$$Q = \left\{ {\begin{array}{*{20}{l}} { - \alpha \frac{{\partial v}}{{\partial x}}}&{{\rm{if}}\:\frac{{\partial v}}{{\partial x}} < 0\:{\rm{or}}\:\frac{{\partial \rho }}{{\partial t}} > 0,}\\ 0&{{\rm{otherwise}},} \end{array}} \right.$$

with α = ρ(kΔx)²∂v/∂x, v being the fluid velocity, ρ the density, Δx the spatial interval, and k a constant parameter whose value is conveniently adjusted in every numerical experiment. This parameter controls the number of zones in which shock waves are spread.

This type of recipe, with minor modifications, has been used in all numerical simulations employing May and White’s formulation, mostly in the context of gravitational collapse, as well as Wilson’s formulation. So, for example, in May and White’s code [133] the artificial viscosity term, obtained in analogy with the one originally proposed by von Neumann and Richtmyer [224], is introduced in the equations accompanying the pressure, in the form

$$Q = \left\{ {\begin{array}{*{20}{l}} {\frac{\rho }{\Gamma }{{\left( {\frac{{a\Delta m}}{{{R^2}}}} \right)}^2}\;\frac{{\partial {R^2}u}}{{\partial m}}}&{{\rm{if}}\:\frac{{\partial \rho }}{{\partial t}} > 0,}\\ 0&{{\rm{otherwise}},} \end{array}} \right.$$

Further examples of equivalent expressions for the artificial viscosity terms, in the context of Wilson formulation, can e.g. be found in [227, 96].

The main advantages of the artificial viscosity approach are:

• (i) It is straightforward to implement (compared to the HRSC schemes which need the characteristic fields of the equations), and

• (ii) it is computationally very efficient.

Experience has shown, however, that this procedure is

• (i) (i) problem dependent and

• (ii) (ii) inaccurate for ultrarelativistic flows [160].

Additionally, the artificial viscosity approach has the implicit difficulty of finding the appropriate form for Q that introduces the necessary amount of dissipation to reduce the spurious oscillations and, at the same time, avoids introducing excessive smearing in the discontinuities. In many instances both properties are difficult to achieve simultaneously. A comprehensive numerical study of artificial viscosity induced errors in strong shock calculations in Newtonian hydrodynamics (including also proposed improvements) was presented by Noh [159].

3.1.2 High-resolution shock-capturing (HRSC) schemes

Since [126] it has been gradually demonstrated [73, 65, 185, 69, 18, 225, 179] that conservative methods exploiting the hyperbolic character of the hydrodynamic equations are optimally suited for accurate integrations, even well inside the ultrarelativistic regime. The explicit knowledge of the characteristic fields (eigenvalues) of the equations, together with the corresponding eigenvectors, provides the mathematical (and physical) framework for such integrations, by means of either exact or approximate Riemann solvers. As further discussed below these solvers compute, at every interface of the numerical grid, the solution of local Riemann problems (i.e., the simplest initial value problem with discontinuous initial data). Hence, a HRSC scheme automatically guarantees that the physical discontinuities appearing in the solution, e.g. shock waves, will be treated consistently (the shock-capturing property). HRSC schemes also produce stable and sharp discrete shock profiles, while providing a high order of accuracy, typically second order or more, in smooth parts of the solution.

To focus the discussion let us consider the system as formulated in Eq. (37). Let us consider a single computational cell of our discrete spacetime. Let Ω be a region (simply connected) of the four-dimensional manifold ${\mathcal M}$, bounded by a closed three-dimensional surface ∂Ω. We take the 3-surface ∂Ω as the standard-oriented hyper-parallelepiped made up of two spacelike surfaces $\{ {\Sigma _{{x^0}}},\:{\Sigma _{{x^0} + \Delta {x^0}}}\}$ plus timelike surfaces $\{ {\Sigma _{{x^i}}},\:{\Sigma _{{x^i} + \Delta {x^i}}}\}$ that join the two temporal slices together. By integrating system (37) over a domain Ω of a given spacetime, the variation in time of the state vector U within Ω is given — keeping apart the source terms — by the fluxes Fⁱ through the boundary ∂Ω. The integral form of system (37)

$$\int_\Omega {\frac{1}{{\sqrt { - g} }}} \frac{{\partial \sqrt \gamma {\rm{U}}}}{{\partial {x^0}}}d\Omega + \int_\Omega {\frac{1}{{\sqrt { - g} }}} \frac{{\partial \sqrt { - g} {{\rm{F}}^i}}}{{\partial {x^i}}}d\Omega = \int_\Omega S d\Omega ,$$

((53))

which can be written in the following conservation form, well-adapted to numerical applications:

$$\begin{array}{*{20}{l}} {{{\left( {{\bar U}\Delta V} \right)}_{{x^0} + \Delta {x^0}}} - {{\left( {{\bar U}\Delta V} \right)}_{{x^0}}}\quad = } \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {\int_{\Sigma_{x^1} + \Delta_{x^1}} {\sqrt { - g} {{{\hat F}}^1}} d{x^0}d{x^2}d{x^3} - \int_{\Sigma_{x^1}} {\sqrt { - g} } {{{\hat F}}^1}d{x^0}d{x^2}d{x^3}} \right)} \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {\int_{\Sigma_{x^2} + \Delta_{x^2}} {\sqrt { - g} {{{\hat F}}^2}} d{x^0}d{x^1}d{x^3} - \int_{\Sigma_{x^2}} {\sqrt { - g} } {{{\hat F}}^2}d{x^0}d{x^1}d{x^3}} \right)} \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {\int_{\Sigma_{x^3} + \Delta_{x^3}} {\sqrt { - g} {{{\hat F}}^3}} d{x^0}d{x^1}d{x^2} - \int_{\Sigma_{x^3}} {\sqrt { - g} } {{{\hat F}}^3}d{x^0}d{x^1}d{x^2}} \right)} \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \int_\Omega {\text{S}} d\Omega ,} \end{array}$$

((54))

where

$${\rm{\bar U}} = \frac{1}{{\Delta V}}\int_{\Delta V} {\sqrt \gamma } {\rm{U}}d{x^1}d{x^2}d{x^3},$$

((55))

$$\Delta V = \int_{{x^1}}^{{x^1} + \Delta {x^1}} {\int_{{x^2}}^{{x^2} + \Delta {x^2}} {\int_{{x^3}}^{{x^3} + \Delta {x^3}} {\sqrt \gamma } } } d{x^1}d{x^2}d{x^3}.$$

((56))

An important property of writing a numerical scheme in conservation form is that, in the absence of sources, the (physically) conserved quantities, according to the partial differential equations, are numerically conserved by the finite difference equations.

The “hat” symbol appearing on the fluxes of Eq. (54) indicates the numerical fluxes. These are recognized as approximations to the time-averaged fluxes across the cell-interfaces, which depend on the solution at those interfaces U(xⁱ + Δxⁱ/2, x⁰) during a time step. At the cell-interfaces the flow conditions can be discontinuous and, following the seminal idea of Godunov [85], the numerical fluxes can be obtained by solving a collection of local Riemann problems. This is depicted in Fig. 2. The continuous solution is locally averaged on the numerical grid, a process which leads to the appearance of discontinuities at the cell-interfaces. Physically, every discontinuity decays into three elementary waves: a shock wave, a rarefaction wave and a contact discontinuity. The complete structure of the Riemann problem can be solved analytically (see [85] for the solution in Newtonian hydrodynamics and [128] in special relativistic hydrodynamics) and, accordingly, used to update the solution forward in time.

Figure 2

Godunov’s scheme: local solutions of Riemann problems. At every interface, x_j-1/2, x_j+1/2, and x_j+3/2, a local Riemann problem is set up as a result of the discretization process (bottom panel), when approximating the numerical solution by piecewise constant data. At time tⁿ these discontinuities decay into three elementary waves which propagate the solution forward to the next time level tⁿ⁺¹ (top panel). The time step of the numerical scheme must satisfy the Courant-Friedrichs-Lewy condition, i.e. be small enough to prevent the waves from advancing more than Δx/2 in Δt.

For reasons of efficiency and, particularly, in multidimensions, the exact solution of the Riemann problem is frequently avoided and linearized (approximate) Riemann solvers are preferred. These solvers are based on the exact solution of Riemann problems corresponding to a linearized version of the original system of equations and, after extensive experimentation, they are found to produce results comparable to those obtained with the exact solver (see [127] for a summary of such approximate solvers in special relativistic hydrodynamics).

In the frame of the local characteristic approach the numerical fluxes are computed according to some generic flux-formula which makes use of the characteristic information of the system. For example, in Roe’s approximate Riemann solver it adopts the following functional form:

$${{\rm{\hat F}}^i} = \frac{1}{2}\left( {{{\rm{F}}^i}\left( {{{\rm{w}}_{\rm{R}}}} \right) + {{\rm{F}}^i}({{\rm{w}}_{\rm{L}}}) - \sum\limits_{n = 1}^5 | {{\tilde \lambda }_n}|\Delta {{\tilde \omega }_n}{{{\rm{\tilde r}}}_n}} \right),$$

((57))

where w_L and w_R represent the values of the primitive variables at the left and right sides, respectively, of the corresponding interface. They are obtained from the cell-centered quantities after a suitable monotone reconstruction procedure. The way these variables are computed determines the spatial order of the numerical algorithm and controls the local jumps at every interface. If these jumps are monotonically reduced, the scheme provides more accurate initial guesses for the solution of the local Riemann problems. A wide variety of cell reconstruction procedures is available in the literature. Among the most popular slope limiter procedures for TVD schemes [89] are the second order piecewise linear reconstruction, introduced by van Leer [220] in the design of the MUSCL scheme (Monotonic Upstream Scheme for Conservation Laws), and the third order piecewise parabolic reconstruction developed by Colella and Woodward [53] in their Piecewise Parabolic Method (PPM). High order piecewise polynomial functions are also available for Essentially Non-Oscillatory (ENO) schemes [90].

The last term in the flux-formula represents the numerical viscosity of the scheme, and it makes explicit use of the characteristic information of the Jacobian matrices of the system. This information is used to provide the appropriate amount of numerical dissipation to obtain accurate representations of discontinuous solutions without excessive smearing, avoiding, at the same time, the growth of spurious numerical oscillations associated with the Gibbs phenomenon. Hence, {̃λ_n, ̃r_n}_n=1…5 are, respectively, the eigenvalues and right-eigenvectors of the Jacobian matrix, and quantities {Δ̃ω_n}_n=1…5 are the jumps of the characteristic variables across each characteristic field. They are obtained by projecting the jumps of the state-vector variables with the left-eigenvectors matrix:

$${\rm{U}}({{\rm{w}}_{\rm{R}}}) - {\rm{U}}({{\rm{w}}_{\rm{L}}}) = \sum\limits_{n = 1}^5 \Delta {\tilde \omega _n}{{\rm{\tilde r}}_n}.$$

((58))

The “tilde” indicates that the corresponding fields are averaged at the cell interfaces from the left and right (reconstructed) values.

During the last few years most of the classical Riemann solvers developed in fluid dynamics have been extended to relativistic hydrodynamics: Eulderink [65], as discussed in Section 2.2.1, has explicitly derived a relativistic Roe Riemann solver [114], Schneider et al. [191] carried out the extension of Einfeldt’s HLLE method [91, 62], Martí and Müller [129] extended the PPM method of Woodward and Colella [234], Wen et al. [225] extended Glimm’s method, Dolezal and Wong [56] put into practice Shu-Osher ENO techniques, Balsara [17] extended Colella’s two-shock approximation and, Donat et al. [57] extended Marquina’s method [58]. The interested reader is referred to [127] for a comprehensive description of such solvers in special relativistic hydrodynamics.

3.2 Other techniques

Two of the most frequently employed alternatives to finite difference schemes in numerical hydrodynamics are Smoothed Particle Hydrodynamics (SPH) and, to a lesser extent, (pseudo-) Spectral Methods.

3.2.1 Smoothed particle hydrodynamics

The Lagrangian particle method SPH, derived independently by Lucy [121] and Gingold and Monaghan [81], has shown successful performance to model fluid flows in astrophysics and cosmology. Most studies to date consider Newtonian flows and gravity, enhanced with the inclusion of the fluid self-gravity.

In the SPH method a finite set of extended Lagrangian particles replaces the continuum of hydrodynamical variables, the finite extent of the particles being determined by a smoothing function (the kernel) containing a characteristic length scale h. The main advantage of this method is that it does not require a computational grid, avoiding mesh tangling and distortion. Hence, compared to grid-based finite volume methods, SPH avoids wasting computational power in multidimensional applications, when, e.g., modeling regions containing large voids. Experience in Newtonian hydrodynamics shows that SPH produces very accurate results with a small number of particles (≈ 10³ or even less). However, if more than 104 particles have to be used for certain problems, and self-gravity has to be included, the computational power, which grows as the square of the number of particles, would exceed the capabilities of current supercomputers. Among the limitations of SPH we note the difficulties in modeling systems with extremely different characteristic lengths and the fact that boundary conditions usually require a more involved treatment than in finite volume schemes.

Reviews of the classical SPH equations are abundant in the literature (see, e.g., [145, 147] and references therein). The reader is addressed to [147] for a summary of comparisons between SPH and HRSC methods.

Recently, implementations of SPH to handle (special) relativistic (and even ultrarelativistic) flows have been developed (see, e.g., [52] and references therein). However, SPH has been scarcely applied to simulate relativistic flows in curved spacetimes. Relevant references include [107, 113, 114, 208].

Following [113] let us describe the implementation of an SPH scheme in general relativity. Given a function f(x), its mean smoothed value 〈f(x)〉, (x = (x, y, z)) can be obtained from

$$\left\langle {f({\rm{x}})} \right\rangle \equiv \int W ({\rm{x}},\:{\rm{x'}};\;h)f({\rm{x'}})\sqrt {g'} {d^3}x',$$

((59))

where W is the smoothing kernel, h the smoothing length and $\sqrt {g'} {d^3}x'$ the volume element. The kernel must be differentiable at least once, and the derivative should be continuous to avoid large fluctuations in the force felt by a particle. Additional considerations for an appropriate election of the smoothing kernel can be found in [82]. The kernel is required to satisfy a normalization condition,

$$\int W ({\rm{x}},\:{\rm{x'}};\;h)\sqrt {g'} {d^3}x' = 1,$$

((60))

which is assured by choosing W(x, x'; h) = ξ(x)Ψ(v), with v = |x - x'|/h, ξ(x) a normalization function, and Ω(v) a standard spherical kernel.

The smooth approximation of gradients of scalar functions can be written as

$$\left\langle {\nabla f({\rm{x}})} \right\rangle = \nabla \left\langle {f({\rm{x}})} \right\rangle - \left\langle {f({\rm{x}})} \right\rangle \nabla \ln \xi ({\rm{x}}),$$

((61))

and that corresponding to the divergence of a vector reads

$$\left\langle {\nabla \;\cdot\;{\rm{A}}({\rm{x}})} \right\rangle = \nabla \;\cdot\;\left\langle {{\rm{A}}({\rm{x}})} \right\rangle - \left\langle {{\rm{A}}({\rm{x}})} \right\rangle \;\cdot\;\ln \xi ({\rm{x}}).$$

((62))

Discrete representations of these procedures are obtained after introducing the number density distribution of particles $\left\langle {n({\rm{x}})} \right\rangle \equiv \sum\nolimits_{a = 1}^N \delta ({\rm{x}} - {{\rm{x}}_a})/\sqrt g$, with {x_a}_a=1,…,N being the collection of N-particles where the functions are known. The previous representations then read:

$$\quad \langle f({{\rm{x}}_a})\rangle \,\quad = \,\quad \xi ({{\rm{x}}_a})\sum\limits_{b = 1}^N {\frac{{f({{\rm{x}}_b})}}{{\langle n({{\rm{x}}_b})\rangle }}} {\Omega _{ab}},$$

((63))

$$\;\;\langle \nabla f({{\rm{x}}_a})\rangle \,\quad = \,\quad \xi ({{\rm{x}}_a})\sum\limits_{b = 1}^N {\frac{{f({{\rm{x}}_b})}}{{\langle n({{\rm{x}}_b})\rangle }}} {\nabla _{{{\rm{x}}_a}}}{\Omega _{ab}},$$

((64))

$$\langle \nabla \:\cdot\:{\rm{A}}({{\rm{x}}_a})\rangle \,\quad = \,\quad \xi ({{\rm{x}}_a})\sum\limits_{b = 1}^N {\frac{{{\rm{A}}({{\rm{x}}_b})}}{{\langle n({{\rm{x}}_b})\rangle }}\:} \cdot\:{\nabla _{{{\rm{x}}_a}}}{\Omega _{ab}},$$

((65))

with Ω,_ab = Ω(x_a, x_b; h). These approximations can be used to derive the SPH version of the general relativistic hydrodynamic equations. Explicit formulae are reported in [113]. The time evolution of the final system of ODEs is performed in [113] using a second-order Runge-Kutta time integrator with adaptive time step. As in non-Riemann solver based finite volume schemes, in SPH simulations involving the presence of shock waves, artificial viscosity terms must be introduced as a viscous pressure term [122].

Recently, Siegler and Riffert [208] have developed a Lagrangian conservation form of the general relativistic hydrodynamic equations for perfect fluids with artificial viscosity in arbitrary background spacetimes. Within that formulation they have built a general relativistic SPH code using the standard SPH formalism as known from Newtonian fluid dynamics (in contrast to previous approaches [122, 107, 113]). The conservative character of their scheme allows the modeling of ultrarelativistic flows including shocks with Lorentz factors as large as 1000.

3.2.2 Spectral methods

The basic principle underlying spectral methods consists of transforming the partial differential equations into a system of ordinary differential equations by means of expanding the solution in a series on a complete basis. The mathematical theory of these schemes is presented in [87, 47]. Spectral methods are particularly well suited to the solution of elliptic and parabolic equations. Good results can also be obtained for hyperbolic equations as long as no discontinuities appear in the solution. When a discontinuity is present some amount of artificial viscosity must be added to obtain a smooth solution. In the specific case of relativistic problems, where coupled systems of elliptic equations (i.e. the Einstein constraint equations) and hyperbolic equations (i.e. hydrodynamics) must be solved, an interesting solution strategy is to use spectral methods for the elliptic equations and HRSC schemes for the hyperbolic ones. Using such combined methods the first results have been obtained in one-dimensional supernova collapse in the framework of a tensor-scalar theory of gravitation [161, 162].

Following [37] we illustrate the main ideas of spectral methods considering the quasi-linear one-dimensional scalar equation:

$$\frac{{\partial u}}{{\partial t}} = \frac{{{\partial ^2}u}}{{\partial {x^2}}} + \lambda u\frac{{\partial u}}{{\partial x}},\:\;\;\;\;t \ge 0,\:\;\;\;x \in [0,1],$$

((66))

with u = u(t, x), and λ a constant parameter. In the linear case (λ = 0), and assuming the function u to be periodic, spectral methods expand the function in a Fourier series:

$$u(x,\;t) = \sum\limits_{k = 0}^\infty {\left[ {{a_k}(t)\cos (2\pi kx) + {b_k}(t)\sin (2\pi kx)} \right].} $$

((67))

From the numerical point of view, the series is truncated for a suitable value of k. Hence, Eq. (66), with λ = 0, can be rewritten as

$$\frac{{d{a_k}}}{{dt}} = - {k^2}{a_k}(t)\:,\:\frac{{d{b_k}}}{{dt}} = - {k^2}{b_k}(t).$$

((68))

Finding a solution of the original equation is then equivalent to solving an “infinite” system of ordinary differential equations, where the initial values of coefficients a_k and b_k are given by the Fourier expansion of u(x, 0).

In the non-linear case, λ ≠ 0, spectral methods, or, in this case, more correctly pseudo-spectral methods, proceed in a more convoluted way: First, the derivative of u is computed in the Fourier space, then they come back to the configuration space by an inverse Fourier transform, multiply ∂u/∂x by u in the configuration space and, finally, come back again to the Fourier space.

The particular set of trigonometric functions used for the expansion is chosen because it automatically fulfills the boundary conditions and because a fast transform algorithm is available. If the initial or boundary conditions are not periodic, Fourier expansion is no longer useful because of the presence of a Gibbs phenomenon at the boundaries of the interval. Legendre or Chebyshev polynomials are, in this case, the most common base of functions used in the expansions (see [87, 47] for a discussion on the different expansions).

A comprehensive summary of applications of (pseudo-) spectral methods in general relativistic astrophysics is presented in [37]. Among those involving time-dependent hydrodynamical simulations we mention the spherically symmetric collapse computations of Gourgoulhon [88] as well as the three-dimensional Newtonian simulations of Bonazzola and Marck et al. [38, 123].

4 Simulations of Astrophysical Phenomena

We turn now to present an overview of strong-field simulations in relativistic astrophysics using the numerical methods discussed in the previous section.

With the exception of the vacuum two-body problem (i.e. the coalescence of two black holes), all realistic astrophysical systems and sources of gravitational radiation involve matter. Thus not surprisingly, the joint integration of the equations of motion for matter and geometry was in the minds of theorists from the very beginning of numerical relativity.

Nowadays there is a large body of numerical investigations in the literature dealing with hydrodynamical integrations in static background spacetimes. Most of those are based on the Wilson formulation of the hydrodynamic equations and use schemes based on finite differences with some amount of artificial viscosity. In more recent years, researchers have started to use conservative formulations of the equations, and their characteristic information, in the design of numerical schemes.

On the other hand, time-dependent simulations of self-gravitating flows in general relativity, evolving the spacetime dynamically with the Einstein equations coupled to a hydrodynamic source, constitute a much smaller sample. Although there is much recent interest in this direction, only the spherically symmetric case (1D) has been extensively studied and, to some extent, can be considered essentially solved. In axisymmetry, i.e. 2D, fewer attempts have been made, with most of them devoted to the study of the gravitational collapse and bounce of rotating stellar cores and the subsequent emission of gravitational radiation. Three-dimensional simulations have only started more recently. The effort is nowadays mainly focused on the study of the coalescence and merging of compact neutron star binaries (as well as the vacuum black hole binary counterpart). These theoretical investigations are driven by the emerging possibility of detecting gravitational waves in a few years time with the different experimental efforts currently underway.

In the following we review the status of the numerical investigations in three astrophysical scenarios all involving strong gravitational fields and, hence, relativistic physics: gravitational collapse, accretion onto black holes and hydro-dynamical evolution of binary neutron stars. Relativistic cosmology, another area where fundamental advances have been accomplished through numerical simulations, is not considered. The interested reader is addressed to the Living Reviews article by Anninos [12] and to the research papers [48, 49, 13].

4.1 Gravitational collapse

The study of gravitational collapse of massive stars has been largely pursued numerically over the years. This problem was already the main motivation when May and White built the first one-dimensional code [133, 134]. It is worth noticing that this code was conceived to integrate the coupled system of Einstein field equations and relativistic hydrodynamics, sidestepping Newtonian approaches.

By browsing through the literature one immediately realizes that the numerical study of gravitational collapse has been neatly split in two main directions since the early investigations. First, the numerical astrophysical community has traditionally focused on the physics of the (type II) Supernova mechanism, i.e., collapse of unstable iron cores followed by a bounce and explosion. Nowadays, numerical simulations are highly developed, as they include rotation and detailed state-of-the-art microphysics (e.g. EOS and sophisticated treatments for neutrino transport). These studies are currently performed routinely, using 3D Cartesian grids with advanced HRSC schemes. Progress in this direction has been achieved, however, at the expense of necessary approximations in the treatment of the hydrodynamics and the gravitational field by using Newtonian physics. In this approach the emission of gravitational radiation is computed through the quadrupole formula. For a recent review of the current status in this direction see [147] and references therein.

On the other hand, the numerical relativity community has been more interested, since the beginning, in highlighting those aspects of the collapse problem having to do with relativistic gravity, in particular the emission of gravitational radiation from a non-spherical collapse. Much of the effort has focused on developing reliable numerical schemes to evolve the gravitational field and much less emphasis, if any, has been given to the details of the microphysics of core collapse. This approach has also considered gravitational collapse leading to black hole formation, employing relativistic hydrodynamics and gravity. Quite surprisingly both approaches have barely interacted over the years, except for a handful of simulations in spherical symmetry. We turn next to their description.

4.1.1 One dimensional simulations

The standard model of type II Supernovae involves the presence of a strong shock wave formed at the edge between the homologous inner core and the outer core which falls at roughly free-fall speed. A schematic illustration of the dynamics of this system is depicted in Fig. 3. The shock is produced after the bounce of the inner core when its density exceeds nuclear density. Numerical simulations have tried to elucidate if this shock would be strong enough to propagate outwards through the star’s mantle and envelope given certain initial conditions for the material in the core, an issue subject to important uncertainties in the nuclear EOS, as well as in the outer layers of the star. In the accepted scenario which has emerged from the numerical simulations, the following features have been found to be necessary for all plausible explosion mechanisms: the existence of the shock wave together with neutrino re-heating that re-energizes it (in the so-called delayed mechanism by which the stalled prompt supernova shock is reactivated by an increase in the pressure behind it due to neutrino energy deposition [229, 28]), and convective overturn which rapidly transports energy into the shocked region [54, 27] (and which can lead to large-scale deviations from spherically symmetric explosions).

Figure 3

Schematic profiles of the velocity versus radius at three different times during core collapse: at the point of “last good homology”, at bounce and at the time when the shock wave has just detached from the inner core.

The path to reach such conclusions has been delineated from numerical simulations in one spatial dimension. Fully relativistic simulations of microphysically detailed core collapse off spherical symmetry are still absent and they could introduce some modifications. The overall picture described above has been demonstrated in multidimensions using sophisticated Newtonian models, as is documented extensively in [147].

May and White’s formulation and their corresponding one-dimensional code formed the basis of the majority of subsequent spherically symmetric codes to study the collapse problem. Wilson [226] investigated the effect of neutrino transport on the stellar collapse concluding that heat conduction by neutrinos does not produce the ejection of material, in contrast to previous results [55, 14]. The code solved the coupled set of hydrodynamic and Einstein equations, supplemented with a Boltzmann transport equation to describe the neutrino flow. Van Riper [222] used a spherically symmetric general relativistic code to study adiabatic collapse of stellar cores, considering the purely hydrodynamical bounce as the preferred explosion mechanism. The important role of general relativistic effects to produce collapses otherwise absent in Newtonian simulations was emphasized. Bruenn [44] developed a code in which the neutrino transport was handled with an approximation, the multigroup flux-limited diffusion. Baron et al. [21] obtained a successful and very energetic explosion for a model with a particularly small value of the incompressibility modulus of symmetric nuclear matter at zero temperature, K ^sym₀ = 180 MeV (whose precise value, nowadays preferred around 240 MeV [84], is still a matter of debate). Mayle et al. [135] computed neutrino spectra from stellar collapse to stable neutron stars for different collapse models using, as [44], multigroup flux-limited diffusion for the neutrino transport. Van Riper [223] and Bruenn [45] verified that a softer supranuclear EOS, combined with general relativistic hydrodynamics, increases the chances for a prompt explosion. In [190, 189] and [137] the neutrino transport was first handled without approximation by using a general relativistic Boltzmann equation. Whereas in [190, 189] the neutrino transport is described by moments of the general relativistic Boltzmann equation in polar slicing coordinates [19], [137] used maximal slicing coordinates. Miralles et al. [142], employing a realistic EOS based upon a Hartree-Fock approximation for Skyrme-type nuclear forces for densities above nuclear density, obtained results qualitatively similar to those of Baron et al. [21], who used a phenomenological EOS, i.e., the explosion was favoured by soft EOS. Swesty et al. [215] also focused on the role of the nuclear EOS in stellar collapse on prompt timescales. Contrary to previous results they found that the dynamics of the shock are almost independent of the nuclear incompressibility, once the EOS is not unphysically softened as in earlier simulations (e.g. [222, 21, 223, 45, 142]). Swesty and coworkers used a finite temperature compressible liquid drop EOS [115]. For the shock to propagate promptly to a large radius they found that the EOS must be very soft at densities just above nuclear densities, which is inconsistent with the 1.44M_⊙ neutron star mass constraint imposed by observations of the binary pulsar PSR 1913+16.

All the aforementioned investigations used artificial viscosity techniques to handle shock waves. Together with a detailed description of the microphysics, the correct numerical modeling of the shock is the major issue in stellar collapse. In this context, the use of HRSC schemes, specifically designed to capture discontinuities, is much more recent. It started in the late eighties with the Newtonian simulations performed by Fryxell et al. [80] using an Eulerian second order PPM scheme (see [147] for a review of the present status). There are only a few relativistic simulations, so far restricted to spherical symmetry. Most of them have been performed by the Valencia group, first employing Newtonian gravity [125], and later relativistic gravity [102, 34, 99, 185]. Martí et al. [125] implemented Glaister’s approximate Riemann solver [83] in a Lagrangian Newtonian hydrodynamical code. They performed a comparison of the energetics of a stellar collapse simulation using this HRSC scheme and a standard May and White code with artificial viscosity for the same initial model, grid size and EOS. They found that the simulation employing a Godunov-type scheme produced larger kinetic energies than that corresponding to the artificial viscosity scheme, with a factor of two difference in the maximum of the infalling velocity. Motivated by this important difference Janka et al. [106] repeated this computation with a different EOS using a PPM second order Godunov-type scheme, disagreeing with Martí et al. [125]. The state-of-the-art implementation of the tensorial artificial viscosity terms in [106] together with the very fine numerical grids employed (unrealistic for three dimensional simulations) could be the reason of the discrepancies.

As mentioned in Section 2.2, Godunov-type methods were first used to solve the equations of general relativistic hydrodynamics in [126], where the characteristic fields of the one-dimensional (spherically symmetric) system were derived. The first astrophysical application was stellar collapse. In [34] the hydrodynamic equations were coupled to the Einstein equations in spherical symmetry. The field equations were formulated as a first-order flux-conservative hyperbolic system for a harmonic gauge [35], somehow “resembling” the hydrodynamic equations. HRSC schemes could be applied, hence, to both systems simultaneously (only coupled through the source terms of the equations). Results for simple models of adiabatic collapse following this approach can be found in [124, 34, 99].

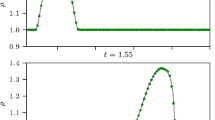
A comprehensive study of adiabatic one-dimensional core collapse using explicit HRSC schemes was presented in [185] (a similar computation using implicit schemes was later performed by [237]). In this investigation the equations for the hydrodynamics and the geometry are written using radial gauge polar slicing (Schwarzschild-type) coordinates. The collapse is modeled with an ideal gas EOS with a non-constant adiabatic index, which varies with the density as Γ = Γ_min + η(log ρ - log ρ_b), where ρ_b is the bounce density and η = 0 if ρ < ρ_b and η > 0 otherwise [222]. A set of animations of the simulations presented in [185] is included in the four MPEG movies in Fig. 4. They correspond to the rather stiff Model B of [185]: Γ_min = 1.33, η = 5 and ρ_b = 2.5 × 10¹⁵ g cm^-3. The initial model is a white dwarf having a gravitational mass of 1.3862M_⊙. The animations show the time evolution of the radial profiles of the following fields: velocity (movie 1), logarithm of the rest-mass density (movie 2), gravitational mass (movie 3) and the square of the lapse function (movie 4).

Figure 4

mpg-Movie (9.02 MB) Stills from a movie showing the animations of a relativistic adiabatic core collapse using HRSC schemes (snapshots of the radial profiles of various variables at different times). The simulations are taken from Ref. [185]: Velocity (figure 1, top-left), logarithm of the rest-mass density (figure 2, top-right), gravitational mass (figure 3, bottom-left) and lapse function squared (figure 4, bottom-right). See text for details of the initial model (For video see appendix).

The movies show that the shock is sharply resolved and free of spurious oscillations. The radius of the inner core at the time of maximum compression, at which the infall velocity is maximum (v = -0.62c), is 6.3 km. The gravitational mass of the inner core at the time of maximum compression is ≈ 1.0M_⊙. The minimum value the quantity α², the lapse function squared, reaches is 0.14, which indicates the highly relativistic character of these simulations (at the surface of a typical neutron star α² ≈ 0.75).

Studies of black hole formation in strong field hydrodynamical simulations of gravitational collapse are less frequent [222, 197, 25, 157]. In [222], using the (Lagrangian) May and White code described above, the mass division between neutron star and black hole formation was considered by means of general relativistic simulations. For the typical (cold) EOS, the critical state was found to lie between the collapses of 1.95M_⊙ and 1.96M_⊙ cores.

In [197] a one-dimensional code based on Wilson’s hydrodynamical formulation was used to simulate a general relativistic (adiabatic) collapse to a black hole. The fluid equations were finite differenced in a mixed Eulerian-Lagrangian form with the introduction of an arbitrary “grid velocity” to ensure sufficient resolution throughout the collapse. The Einstein equations were formulated following the ADM equations. Isotropic coordinates and a maximal time slicing condition were used to avoid the physical singularity once the black hole forms. Due to the non-dynamical character of the gravitational field in the case of spherical symmetry (i.e., the metric variables can be computed at every time step solving elliptic equations) this code was able to follow relativistic configurations for many collapse time scales Δt ≫ GM/c³ after the initial appearance of an event horizon.

A Lagrangian scheme based on the Misner and Sharp [143] formulation for spherically symmetric gravitational collapse (as in [222]) was developed by Miller and Motta [140] and later by Baumgarte, Shapiro and Teukolsky [25]. The novelty of these codes was the use of an outgoing null coordinate u (an “observer-time” coordinate, as suggested previously by [97]) instead of the usual Schwarzschild time t appearing in the Misner and Sharp equations. These coordinates are ideally suited to study black hole formation as they never cross the black hole event horizon. In these codes the Hernńndez-Misner equations [97] (or, alternatively, the Misner-Sharp equations) were solved by an explicit finite difference scheme similar to [222]. In [140] the collapse of an unstable polytrope, followed to black hole formation, was first achieved using null slicing. In [25] the collapse of a 1.4M_⊙ polytrope with Γ = 4/3 to a black hole was compared to [222], using the Misner-Sharp equations, finding a 10% agreement. However, the evolution stopped after the formation of the apparent horizon. This work demonstrated numerically that the use of a retarded time coordinate allowed for much longer evolutions after black hole formation. The Lagrangian character of both codes has prevented their multidimensional extension.

Recently, Neilsen and Choptuik [157] have studied critical collapse of a spherically symmetric perfect fluid with the EOS p = (Γ - 1)ρ using a conservative form of the hydrodynamic equations and HRSC schemes. Critical phenomena in gravitational collapse were first discovered numerically in simulations of the massless Klein-Gordon field minimally coupled to gravity [51]. Since then critical phenomena arising at the threshold of black hole formation, in parametrized families of collapse, have been found in a variety of physical systems, including the perfect fluid model. The Einstein equations coupled to the hydrodynamic equations were integrated in [157] in spherical symmetry adopting the ADM formalism. The use of a conservative formulation and numerical schemes well adapted to describe ultrarelativistic flows [158] made it possible to find evidence for the existence of critical solutions for large values of the adiabatic index Γ (1.89 ≤ Γ ≤ 2), extending the previous upper limit.

One-dimensional numerical simulations of self-gravitating matter accreting onto a black hole, formed after the gravitational collapse of a massive star, have been performed in [172]. Using the formulation outlined in Section 2.2.2 and HRSC schemes, Papadopoulos and Font [172] performed the simulations adopting an ingoing null foliation of a spherically symmetric black hole spacetime. Such a foliation has the interesting property of penetrating the black hole horizon, allowing for an unambiguous numerical treatment of the inner boundary. The simulations reported in [172] describe the capture of an initial Gaussian shell distribution of perfect fluid matter by a non-rotating black hole. The results show that the accretion process initiates, as expected, a rapid increase of the mass of the apparent horizon. This is depicted in Fig. 5. The horizon almost doubles its size during the first 10M – 15M (this is enlarged in the insert of Fig. 5). Once the main accretion process has finished, the mass of the horizon slowly increases in a quasi-steady manner, whose rate depends on the mass accretion rate imposed at the world-tube of the integration domain.

Figure 5

Evolution of the black hole apparent horizon mass during the spherical accretion of a self-gravitating perfect fluid whose density is parametrized according to ρ = ρ_b + ρ_m exp(-σ(r - r_c)²) with ρ_m = 10^-4, σ = 0.1 and r_c = 6M. The background density ρ_b is given by the spherical Michel solution [138]. The grid extends from r_min = 1.1M to r_max = 20M. The mass of the apparent horizon shows a rapid increase in the first 15M (enlarged in the insert), in coincidence with the most dynamical accretion phase. The slow, quasi-steady growth at later times is the quiet response of the black hole to the low mass accretion rate imposed at the world tube.

4.1.2 Multidimensional studies

The use of general relativistic axisymmetric codes in numerical astrophysics has been largely devoted to the study of the gravitational collapse and bounce of a rotating stellar core and the subsequent emission of gravitational radiation. These studies of axisymmetric scenarios started in the early eighties when the available computer resources were still inadequate to attempt three dimensional simulations. The collapse scenario was by then the main motivation for code builders in numerical relativity, as it was considered one of the most important gravitational wave sources, in the same way as the coalescence and merging of neutron star (and/or black hole) binaries is driving the development of fully three dimensional codes in the nineties (and possibly will continue during the forthcoming years) in correlation with the increasing availability of computer power.

All numerical studies of axisymmetric gravitational collapse in general relativity, which will be briefly discussed next, have used Wilson’s formulation of the hydrodynamic equations and finite difference schemes with artificial viscosity. The problem has not yet been considered in two (and three) dimensions using conservative formulations and HRSC schemes.

The investigations of the collapse problem started with the work of Nakamura [149], who was the first to calculate a general relativistic rotating stellar collapse. He adopted the (2+1)+1 formulation of the Einstein equations in cylindrical coordinates and introduced regularity conditions to avoid divergence behavior at coordinate singularities (the plane Z = 0) [150]. The equations were finite differenced using the donor cell scheme plus Friedrichs-Lax type viscosity terms. Nakamura used a “hypergeometric” slicing condition (which reduces to maximal slicing in spherical symmetry) which prevents the grid points from hitting the singularity if a black hole forms. The simulations could track the evolution of the collapsing (perfect fluid) matter and the formation of a black hole. However, the scheme was not accurate enough to compute the emitted gravitational radiation. The reason is that the energy emitted in this process as gravitational radiation is very small compared to the total rest mass energy, making its accurate numerical computation very challenging.

In a series of papers [19, 212, 178, 213], Bardeen, Stark and Piran revisited this problem studying the collapse of rotating relativistic polytropic stars to black holes, succeeding in computing the gravitational radiation emission. The field and hydrodynamic equations were formulated using the 3+1 formalism with radial gauge and a mixture of (singularity avoiding) polar and maximal slicing. Their parameter space survey showed how black hole formation (of the Kerr class) occurs only for angular momenta less than a critical value. Their numerical results also demonstrated that the gravitational wave emission from axisymmetric rotating collapse to a black hole was very low, ΔE/Mc² < 7 × 10^-4, and that the general waveform shape was nearly independent of the details of the collapse. Concerning this we note that, in a previous investigation, Müller [146] obtained the first numerical evidence of the low gravitational efficiency of the core-collapse scenario. By means of axisymmetric Newtonian simulations he found that E < 10^-6Mc² was radiated as gravitational waves.

Evans [66], building on previous work by Dykema [60], also studied the gravitational collapse problem for non-rotating matter configurations. His numerical scheme to integrate the matter fields was more sophisticated than in the previous approaches as it included monotonic upwind reconstruction procedures and flux limiters. Discontinuities appearing in the flow solutions were stabilized by adding artificial viscosity terms in the equations, following Wilson’s approach. Evans [66] was able to show that Newtonian gravity and the quadrupole formula for gravitational radiation were inadequate to study the problem.

Most of the aforementioned axisymmetric codes adopted spherical polar coordinates. Numerical instabilities are encountered at the origin (r = 0) and, mainly, at the polar axis (θ = 0, π) where some fields diverge due to the coordinate singularities. Evans did important contributions towards regularizing the gravitational field equations in such situations [66]. These coordinate problems have deterred researchers from building three-dimensional codes in spherical coordinates. In this case Cartesian coordinates are adopted which, despite the desired property of being everywhere regular, present the important drawback of not being adapted to the topology of astrophysical systems. As a result this has important consequences on the grid resolution requirements. The only extension of an axisymmetric 3+1 code using spherical coordinates to three dimensions has been accomplished by Stark [211], although no applications in relativistic astrophysics have yet been presented.

Alternatively, existing axisymmetric codes employing the characteristic formulation of the Einstein equations [233], such as the (vacuum) one presented in [86], do not share the axis instability problems of 3+1 codes. Hence, axisymmetric characteristic codes, once conveniently coupled to matter fields, could be a promising way of studying the axisymmetric collapse problem.

In a much simpler approach some investigations have considered dynamical evolutions of a collisionless gas of particles in full general relativity [198, 199, 200, 201, 5]. Such pressureless particles move along geodesics of the spacetime. The geodesic equations are, in comparison to the hydrodynamic equations, trivial to integrate. All efforts can focus then on solving the gravitational field equations. Shapiro and Teukolsky [198, 199] built a code to solve the Vlasov equation in general relativity by N-body particle simulation, computing the gravitational field using the ADM formalism. They studied the origin of quasars and active galactic nuclei via the collapse of relativistic star clusters to supermassive black holes. They also considered the collapse of prolate spheroids finding that if those are sufficiently compact, the final singularities are hidden inside black holes. On the controversial side, however, they found that when the spheroids are large enough there are no apparent horizons, in disagreement with the cosmic censorship hypothesis [175], because a naked singularity may form in non-spherical relativistic collapse [200]. Collapses with small enough angular momentum also showed the same behavior [201]. However, such computations have not yet been attempted using a fully hydrodynamical code, with the inclusion of pressure effects. Hence, the possibility of naked singularity formation in more realistic numerical simulations still remains to be analyzed.

Semi-analytical studies of finite-sized collections of dust, shaped in the form of stars or shells, falling isotropically onto a black hole are available in the literature [152, 92, 202, 164, 177]. These investigations approximate gravitational collapse by a dust shell of mass m falling into a Schwarzschild black hole of mass M ≫ m. These studies have shown that for a fixed amount of infalling mass the gravitational radiation efficiency is reduced compared to the point particle limit, never exceeding that of a particle with the same mass, the reason being cancellations of the emission from distinct parts of the extended object.

In [171] such conclusions were corroborated with a numerical simulation of the gravitational radiation emitted during the accretion process of an extended object onto a black hole. The first order deviations from the exact black hole geometry were approximated using curvature perturbations induced by matter sources whose non-linear evolution was integrated using a (non-linear) hydrodynamical code (adopting the Valencia conservative formulation and HRSC schemes). All possible types of curvature perturbations are captured in the real and imaginary parts of the Weyl tensor scalar (see, e.g., [50]). In the framework of the Newman-Penrose formalism the equations for the perturbed Weyl tensor components decouple, and when written in the frequency domain even separate [217]. Papadopoulos and Font [171] used the limiting case for Schwarzschild black holes, i.e. the inhomogeneous Bardeen-Press equation [20]. The simulations showed the gradual excitation of the black hole quasi-normal mode frequency by sufficiently compact shells.

An example of these simulations appears in the MPEG movie of Fig. 6. This movie shows the time evolution of the shell density (left panel) and the associated gravitational waveform during a complete accretion/collapse event. The (quadrupolar) shell is parametrized according to $\rho = {\rho _0} + {e^{ - k(r* - r0)}}^{^2}{\sin ^2}\theta$ with k = 2, ρ₀ = 10^-2 and r₀ = 35M. Additionally r_* denotes a logarithmic radial (Schwarzschild) coordinate. The animation shows the gradual collapse of the shell onto the black hole. This process triggers the emission of gravitational radiation. In the movie it can be clearly seen how the burst of the emission coincides with the more dynamical accretion phase, when the shell crosses the peak of the potential and is subsequently captured by the hole. The gravitational wave signal coincides with the quasinormal ringing frequency of the black hole, 17M. The existence of an initial burst, causally separated from the physical burst, is also noticeable in the movie. It just reflects the gravitational radiation content of the initial data (see [171] for a detailed explanation).

Figure 6

mpg-Movie (2.03 MB) Stills from a movie showing the time evolution of the accretion/collapse of a quadrupolar shell onto a Schwarzschild black hole. The left panel shows isodensity contours and the right panel the associated gravitational waveform. The shell, initially centered at r_* = 35M, is gradually accreted by the black hole, a process which perturbs the black hole and triggers the emission of gravitational radiation. After the burst, the remaining evolution shows the decay of the black hole quasi-normal mode ringing. By the end of the simulation a spherical accretion solution is reached. Further details are given in [171].(For video see appendix)

We end this section by pointing out that, to date, there are no three-dimensional relativistic simulations of gravitational collapse in the context of supernova core collapse yet available. All the existing computations have been done employing Newtonian physics. We point out, however, that this situation may change in the near future, as very recently the first fully relativistic three-dimensional simulations of gravitational collapse leading to black hole formation have been performed for rapidly-rotating supramassive neutron stars [204], for the head-on collision of two neutron stars [141], or for the coalescence of neutron star binaries [203, 206] (see Section 4.3).

Bonazzola and Marck [38] performed the first three-dimensional simulations, using pseudo-spectral methods, very accurate and free of numerical or intrinsic viscosity. They confirmed the low amount of energy radiated in gravitational waves regardless of the initial conditions of the collapse: axisymmetric, rotating or tidally deformed. Their results are only applicable to the pre-bounce phase of the supernova collapse as the simulations do not consider shock propagation after bounce.

The more detailed multi-dimensional non-relativistic simulations are those performed by the MPA/Garching group (an on-line sample can be found at their website [3]). As mentioned before these include sophisticated microphysics and employ accurate HRSC integration schemes. To illustrate the degree of sophistication achieved in Newtonian simulations we present in the MPEG movie in Fig. 7 an animation of the early evolution of a core collapse supernova explosion up to 220 ms after core bounce and shock formation (only an intermediate snapshot at 130 ms is depicted in Fig. 7). The movie shows the evolution of the entropy within the innermost 3000 km of the star.

Figure 7

mpg-Movie (3.37 MB) Still from a movie showing the animation of the time evolution of the entropy in a core collapse supernova explosion [108]. The movie shows the evolution within the innermost 3000 km of the star and up to 220 ms after core bounce. See text for explanation. (For video see appendix)

The initial data used in these calculations are taken from the 15M_⊙ precollapse model of a blue supergiant star of [236]. The computations start 20 ms after core bounce from a one-dimensional model of [46]. This model is obtained with the one-dimensional general relativistic code mentioned previously [44] which includes a detailed treatment of the neutrino physics and a realistic EOS, and which is able to follow core collapse, bounce and the associated formation of the supernova shock. Because of neutrino cooling and energy losses due to the dissociation of iron nuclei the shock initially stalls inside the iron core.

The movie shows how the stalling shock is “revived” by neutrinos streaming from the outer layers of the hot, nascent neutron star in the center. A negative entropy gradient builds up between the so-called “gain-radius”, which is the position where cooling of hot gas by neutrino emission switches into net energy gain by neutrino absorption, and the shock further out. Convective instabilities therefore set in, which are characterized by large rising blobs of neutrino heated matter and cool, narrow downflows. The convective energy transport increases the efficiency of energy deposition in the post-shock region by transporting heated material near the shock and cooler matter near the gain radius where the heating is strongest. The freshly heated matter then rises again while the shock is distorted by the upward streaming bubbles. The reader is addressed to [108] for a more detailed description of a more energetic initial model.

4.2 Accretion onto black holes

The study of relativistic accretion and black hole astrophysics is currently a very active field of research, both theoretically and observationally (see, e.g., [31] and references therein). On the theoretical side, since the pioneering work by Shakura and Sunyaev [195] thin disk models, parametrized by the so-called α-viscosity, in which the gas rotates with Keplerian angular momentum which is transported radially by viscous stress, have been applied successfully to many astronomical objects. The thin disk model, however, is not valid for high luminosity systems, as it is unstable at high mass accretion rates. In this regime Abramowicz et al. [8] found a new solution, called the slim disk solution, which is stable against viscous and thermal instabilities. More recently, much theoretical work has been devoted to the problem of slow accretion, motivated by the discovery that many galactic nuclei are under-luminous (e.g. NGC 4258). Proposed accretion models involve the existence of advection-dominated accretion flows (ADAF solution; see, e.g., [156, 154]) or, more recently, advection-dominated inflow outflow solutions (ADIOS solution [32]). The self-similar global ADAF solutions provide an excellent description of systems such as the Galactic center SgrA^* and quiescent soft X-ray transients. In particular they can reproduce very accurately observed spectra from radio to X-ray frequencies. ADAF solutions have been very successfully applied to non-rotating black holes using a pseudo-Newtonian potential [168], and they have also been extended to the Kerr spacetime (e.g. [7]). Current investigations try to solve the uncertainty concerning the location of the transition radius in a two-component accretion flow, i.e. the radius between the inner ADAF solution and the outer geometrically thin disk.

On the other hand, advances in satellite instrumentation, e.g. the Rossi X-Ray Timing Explorer (RXTE), and the Advanced Satellite for Cosmology and Astrophysics (ASCA), are greatly stimulating, and are guiding theoretical research on accretion physics. The recent discovery of kHz quasi-periodic oscillations in low-mass X-ray binaries extends the frequency range over which these oscillations occur into timescales associated with the innermost regions of the accretion process (for a review see [219]). Moreover, in extragalactic sources spectroscopic evidence (broad iron emission lines) increasingly points to (rotating) black holes being the accreting central objects [216, 112, 43].

Additionally, most of the proposed theoretical models to explain γ-ray bursts involve a, possibly hyper-accreting, black hole at some point of the evolutionary paths [180]: neutron star-neutron star and black hole-neutron star binaries, collapsars, black hole-white dwarf binaries, or common envelope evolution of compact binary systems. Developing the capability of performing accurate numerical simulations of time-dependent accretion flows in regions of strong gravitational fields, possibly dynamic during the hyper-accreting phase, is indeed of enormous interest.

Accretion theory is primarily based on the study of (viscous) stationary flows and their stability properties through linearized perturbations thereof. A well-known example is the solution consisting of isentropic constant angular momentum tori, unstable to a variety of non-axisymmetric global modes, discovered by Papaloizou and Pringle [173] (see [16] for a review of instabilities in astrophysical accretion disks). Establishing the nature of flow instabilities requires highly resolved and accurate time-dependent non-linear numerical investigations in strong gravitational fields. Such simulations have only been attempted, in general relativity, in a few cases and only for inviscid flows.

For a wide range of accretion problems, the Newtonian theory of gravity is adequate for the description of the background gravitational forces (see, e.g., [78]). The extensive experience with Newtonian astrophysics has shown that explorations of the relativistic regime benefit from the use of model potentials. Among those, we mention the Paczyński-Wiita pseudo-Newtonian potential for a Schwarzschild black hole [168], which gives approximations of general relativistic effects with accuracy of 10% – 20% in regions from the black hole larger than the marginally stable radius, which corresponds to three times the Schwarzschild radius. Nevertheless, for comprehensive numerical work, a full (i.e. three-dimensional) formalism is required, able to cover also the maximally rotating hole. In rotating spacetimes the gravitational forces cannot be captured fully with scalar potential formalisms. Additionally, geometric regions such as the ergo-sphere would be very hard to model without a metric description. Whereas the bulk of emission occurs in regions with almost Newtonian fields, only the observable features attributed to the inner region may crucially depend on the nature of the spacetime.

In the following we present a summary of illustrative time-dependent accretion simulations in relativistic hydrodynamics. We concentrate on multidimensional simulations. In the limit of spherical accretion, exact stationary solutions exist for both Newtonian gravity [39] and relativistic gravity [138]. Such solutions are commonly used as test-beds of time-dependent hydrodynamical codes, by analyzing whether stationarity is maintained during a numerical evolution [96, 126, 65, 185, 18].

4.2.1 Time-dependent disk accretion simulations

Pioneering numerical efforts in the study of black hole accretion [227, 96, 93, 94] made use of the the so-called frozen star paradigm of a black hole. In this framework, the time “slicing” of the spacetime is synchronized with that of asymptotic observers far from the hole. Within this approach Wilson [227] first investigated numerically the time-dependent accretion of inviscid matter onto a rotating (Kerr) black hole. This was the first problem to which his formulation of the hydrodynamic equations, as presented in Section 2.1.2, was applied. Wilson used an axisymmetric hydrodynamical code in cylindrical coordinates studying the formation of shock waves and the X-ray emission in the strong-field regions close to the black hole horizon, being able to follow the formation of thick accretion disks during the simulations.

Wilson’s formulation has been extensively used in time-dependent numerical simulations of disk accretion. In [96] (see also [93]) Hawley and collaborators studied, in the test-fluid approximation and axisymmetry, the evolution and development of non-linear instabilities in pressure-supported accretion disks formed as a consequence of the spiraling infall of fluid with some amount of angular momentum. Their initial models were computed following the analytic theory of relativistic disks presented by Abramowicz et al. [6]. The code used explicit second-order finite difference schemes with a variety of choices to integrate the transport terms of the equations (i.e. those involving changes in the state of the fluid at a specific volume in space). The code also used a staggered grid (with scalars located at the cell centers and vectors at the cell boundaries) for its suitability to difference the transport equations. Discontinuous solutions were stabilized with artificial viscosity terms.

With a three-dimensional extension of the axisymmetric code of Hawley, Smarr, and Wilson [95, 96], Hawley [94] studied the global hydrodynamic non-axisymmetric instabilities in thick, constant angular momentum accretion gas tori, orbiting around a Schwarzschild black hole. Such simulations showed that in radially wide, nearly constant angular momentum tori, the Papaloizu-Pringle instability saturates in a strong spiral pressure wave, not in turbulence. In addition, the simulations confirmed that accretion flows through the torus could reduce and even halt the growth of the global instability.

Igumenshchev and Beloborodov [103] have performed two-dimensional relativistic hydrodynamical simulations of inviscid transonic disk accretion onto a rotating (Kerr) black hole. The hydrodynamical equations follow Wilson’s formulation but the code avoids the use of artificial viscosity. The advection terms are evaluated with an upwind algorithm which incorporates the PPM scheme [53] to compute the fluxes. Their numerical work confirms analytical expectations:

• (i) The structure of the innermost disc region strongly depends on the black hole spin, and

• (ii) the mass accretion rate goes as ̇M ∝ (ΔW)^Γ/(Γ-1), ΔW being the energy gap at the cusp of the torus (i.e. ΔW = W₀ - W_cusp, W₀ being the potential at the boundary of the torus) and Γ the adiabatic index.

Yokosawa [238, 239], also using Wilson’s formulation, studied the structure and dynamics of relativistic accretion disks and the transport of energy and angular momentum in magneto-hydrodynamical accretion onto a rotating black hole. In his code the hydrodynamic equations are solved using the Flux-Corrected-Transport (FCT) scheme [42] (a second-order flux-limiter method in smooth regions which avoids oscillations near discontinuities by reducing the magnitude of the numerical flux), and the magnetic induction equation is solved using the constrained transport method [67]. The code contains a parametrized viscosity based on the α-model [195]. The simulations revealed different flow patterns, inside the marginally stable orbit, depending on the thickness h of the accretion disk. For thick disks with h ≥ 4r_h, r_h being the radius of the event horizon, the flow pattern becomes turbulent.

4.2.2 Wind accretion simulations

The term “wind” or hydrodynamic accretion refers to the capture of matter by a moving object under the effect of the underlying gravitational field. The canonical astrophysical scenario in which matter is accreted in such a non-spherical way was suggested originally by Bondi, Hoyle and Lyttleton [98, 40], who studied, using Newtonian gravity, the accretion onto a gravitating point mass moving with constant velocity through a non-relativistic gas of uniform density. The matter flow inside the accretion radius, after being decelerated by a conical shock, is ultimately captured by the central object. Such a process applies to describe mass transfer and accretion in compact X-ray binaries, in particular in the case in which the donor (giant) star lies inside its Roche lobe and loses mass via a stellar wind. This wind impacts on the orbiting compact star forming a bow-shaped shock front around it. Such an accretion process is also thought to take place during common envelope evolution of a binary system.

Since those analytic studies numerical simulations by an increasing number of authors (see, e.g., [186, 26] and references therein) have extended the simplified analytic models and have helped to develop a thorough understanding of the hydrodynamic accretion scenario in its fully three-dimensional character. These investigations have revealed the formation of accretion disks and the appearance of non-trivial phenomena such as shock waves or flip-flop (tangential) instabilities.

Most of the existing numerical work has used Newtonian hydrodynamics to study the accretion onto non-relativistic stars. For compact accretors such as neutron stars or black holes the correct numerical modeling requires a general relativistic hydrodynamical description. Within the relativistic frozen star framework, wind accretion onto “moving” black holes was first studied in axisymmetry by Petrich et al. [176]. In this work Wilson’s formulation of the hydrodynamic equations was adopted. The integration algorithm was taken from [213] with the transport terms finite-differenced following the prescription given in [96]. An artificial viscosity term of the form Q = aρ(Δv)², with a being a constant, was added to the pressure terms of the equations.

More recently, an extensive survey of the morphology and dynamics of relativistic wind accretion past a Schwarzschild black hole was performed in [72, 71]. This investigation differs from [176] in both the use of a conservative formulation for the hydrodynamic equations (the Valencia formulation; see Section 2.1.3) and the use of advanced HRSC schemes. Axisymmetric computations were compared to [176], finding major differences in the shock location, opening angle, and accretion rates of mass and momentum. The reasons for the discrepancies may be diverse and related to the use of different formulations, numerical schemes and, possibly, to the grid resolution. In [176] canonical grid sizes were extremely coarse, of 40 × 20 zones in r and cos θ respectively. The simulations presented in [72, 71] used much finer grids in every direction.

Non-axisymmetric two-dimensional studies, restricted to the equatorial plane of the black hole, were first performed in [71], motivated by the non-stationary patterns found in Newtonian simulations (see, e.g., [26]). The relativistic computations revealed that initially asymptotic uniform flows always accrete onto the hole in a stationary way which closely resembles the previous axisymmetric patterns.

Papadopoulos and Font [170] have recently presented a procedure which considerably simplifies the numerical integration of the general relativistic hydrodynamic equations near black holes. Their procedure is based on identifying classes of coordinates in which the black hole metric is free of coordinate singularities at the horizon (unlike the commonly adopted Boyer-Lindquist coordinates), independent of time, and admits a spacelike decomposition. With those coordinates the innermost radial boundary can be placed inside the horizon, allowing for a clean treatment of the entire (exterior) physical domain. In [180] Michel’s (spherical) solution was re-derived using a particular coordinate system adapted to the black hole horizon, the Eddington-Finkelstein system. In Fig. 8 a representative sample of hydrodynamical quantities is plotted for this stationary solution. The solid lines correspond to the exact solution and the symbols correspond to the numerical solution. The solution is regular well inside the horizon at r = 2M. The steepness of the hydrodynamic quantities dominates the solution only near the real singularity.

Figure 8

Exact (solid line) versus numerical (circles) solution for spherical accretion of a perfect fluid in Eddington-Finkelstein coordinates [170]. The solution extends inside the event horizon of the black hole at r = 2M, where all fields are smooth, only blowing up at the central singularity at r = 0.

In [74, 75] this approach was applied to the study of relativistic wind accretion onto rapidly rotating (Kerr) black holes. The effects of the black hole spin on the flow morphology were found to be confined to the inner regions of the black hole potential well. Within this region, the black hole angular momentum drags the flow, wrapping the shock structure around. An illustrative example is depicted in Fig. 9. The left panel of this figure corresponds to a simulation employing the Kerr-Schild form of the Kerr metric, regular at the horizon. The right panel shows how the accretion pattern would look like, were the computation performed using the more common Boyer-Lindquist coordinates. The transformation induces a noticeable wrapping of the shock around the central hole. The shock would wrap infinitely many times before reaching the horizon. As a result, the computation in these coordinates would be much more challenging than in Kerr-Schild coordinates.

Figure 9

Relativistic wind accretion onto a rapidly rotating Kerr black hole (a = 0.999M, the hole spin is counter-clock wise) in Kerr-Schild coordinates (left panel). Isocontours of the logarithm of the density are plotted at the final stationary time t = 500M. Brighter colors (yellow-white) indicate high density regions while darker colors (blue) correspond to low density zones. The right panel shows how the flow solution looks like when transformed to Boyer-Lindquist coordinates. The shock appears here totally wrapped around the horizon of the black hole. The box is 12M units long. The simulation employed a (r, ϕ)-grid of 200 × 160 zones. Further details are given in [74].

4.3 Hydrodynamical evolution of neutron stars

The numerical evolution of neutron stars in general relativity is nowadays a very active field of research [207, 131, 76, 141, 203, 204, 206, 77]. The numerical investigation of many interesting astrophysical processes involving neutron stars, such as the rotational evolution of proto-neutron stars or the gravitational radiation from unstable pulsation modes or, more importantly, from the catastrophic coalescence and merger of neutron star-neutron star or black hole-neutron star binaries, requires the ability to perform accurate long-term hydrodynamical evolutions employing relativistic gravity.

Evolutions of polytropic models of spherical neutron stars (i.e. with EOS p = Kρ^Γ, K being the polytropic constant) using relativistic hydrodynamics can be used as test-bed computations for multidimensional codes. One-dimensional hydrodynamical studies of relativistic stars have been performed by [88], employing pseudo-spectral methods, and by [185] with HRSC schemes. These investigations adopted radial gauge polar slicing coordinates in which the general relativistic equations are expressed in a simple way which resembles Newtonian hydrodynamics. Gourgoulhon [88] used a numerical code to detect, dynamically, the zero value of the fundamental mode of a neutron star against radial oscillations. Romero et al. [185] highlighted the accuracy of HRSC schemes by finding, numerically, a change in the stability behavior of two slightly different initial neutron star models: A model with mass 1.94532M_⊙ is stable and a model of 1.94518M_⊙ is unstable.

Three-dimensional hydrodynamical evolutions of relativistic, self-gravitating neutron stars have been considered in [76, 203, 9, 204, 206]. In [76] a new efficient parallel general relativistic hydrodynamical code was presented and thoroughly tested. In this code the Valencia hydrodynamical (conservative) formulation was adopted and a variety of state-of-the-art Riemann solvers were implemented, including Roe’s solver [184] and Marquina’s flux formula [58]. The Einstein equations were formulated using two different approaches:

• (i) the standard ADM formalism and

• (ii) a hyperbolic formulation developed in [36].

The code was subjected to a series of convergence tests, with (twelve) different combinations of the spacetime and hydrodynamics finite differencing schemes, demonstrating the consistency of the discrete equations with the differential equations. The simulations performed in [76] include, among others, the evolution of equilibrium configurations of compact stars (solutions to the TOV equations), and the evolution of relativistically boosted TOV stars (v = 0.87c) transversing diagonally across the computational domain. In the long term plan this code is designed to simulate the inspiral coalescence of two neutron stars in general relativity. The more “academic” scenario of a head-on collision has been already analyzed in [141] and is briefly described below.

The simulations presented in [203, 204, 206, 9] are performed using a reformulation of the ADM equations, first proposed by Shibata and Nakamura [205], and recently taken up by Baumgarte and Shapiro [24]. This formulation is based upon a conformal decomposition of the three metric and extrinsic curvature. Additionally, three “conformal connection functions” are introduced so that the principal part of the conformal Ricci tensor is an elliptic operator acting on the components of the conformal three metric. In this way the evolution equations reduce to a coupled set of non-linear, inhomogeneous wave equations for the conformal three metric, which are coupled to evolution equations for the (gauge) connection functions. Further details can be found in [24]. This formulation has proven to be much more long-term stable (though somehow less accurate, see [9]) than standard ADM. The tests analyzed include evolutions of weak gravitational waves [24], self-gravitating matter configurations with prescribed (analytic) time evolution [23], spherical dust collapse [203], strong gravitational waves (which even collapse to black holes) [9], black holes [9], and boson stars [9]. Hydrodynamical evolutions of neutron stars are extensively considered in [203, 204, 206].

Nowadays, most of the current efforts in developing codes in relativistic astrophysics are strongly motivated by the simulation of the coalescence of compact binaries. These scenarios are considerered the most promising sources of gravitational radiation to be detected by the planned laser interferometers going online worldwide in the next few years. The computation of the gravitational waveform during the most dynamical phase of the coalescence stage depends crucially on hydrodynamical finite-size effects. This phase begins once the stars, initially in quasi-equilibrium orbits of gradually smaller orbital radius, due to the emission of gravitational waves, reach the innermost stable circular orbit (see the schematic plot in Fig. 10). From here on, the final merger of the two objects takes place in a dynamical timescale and lasts for a few milliseconds. A treatment of the gravitational radiation as a perturbation in the quadrupole approximation would be valid as long as M/R ≪ 1 and M/r ≪ 1 simultaneously, M being the mass of the binary, R the neutron star radius and r the separation of the two stars. As the stars gradually approach each other and merge, both inequalities are less valid and fully relativistic calculations become necessary.

Figure 10

Schematic illustration showing the evolution of a neutron star binary (left side) together with the numerical approach (right side) best suited for an accurate description of each portion of the evolution. General relativistic hydro-dynamic simulations are unavoidable during the most dynamical phase from the innermost stable circular orbit to the final merge.

The accurate simulation of a binary neutron star coalescence is however one of the most challenging tasks in numerical relativity. These scenarios involve strong gravitational fields, matter motion with (ultra-) relativistic speeds and/or strong shock waves. The difficulties of a successful numerical integration are exacerbated by the intrinsic multidimensional character of the problem and by the inherent complexities in Einstein’s theory of gravity, e.g. coordinate degrees of freedom and the possible formation of curvature singularities (e.g. collapse of matter configurations to black holes).

For these reasons it is not surprising that most of the available simulations have been attempted in the Newtonian (and post-Newtonian) framework. Most of these studies employ Lagrangian particle methods such as SPH, and only a few have considered (less viscous) high-order finite difference methods such as PPM [17]. The interested reader is referred to the recent review by Rasio and Shapiro [181] and an upcoming Living Reviews article by Swesty [214], for detailed descriptions of the current status of Newtonian simulations.

Concerning relativistic simulations Wilson’s hydrodynamical formulation has been applied to the study of neutron star binary coalescence in [231, 232] under the assumption of a conformally flat spacetime, which leads to a considerable simplification of the gravitational field equations. In this case they reduce to a coupled set of elliptic (Poisson-like) equations for the lapse function, shift vector and conformal factor. Their simulations revealed, unexpectedly, the appearance of a “binary-induced collapse instability” of the neutron stars, prior to the eventual collapse of the final merged object, with the central density of each star increasing by an amount proportional to 1/r. The numerical results of Wilson and collaborators have received considerable attention in the literature, and their unexpected outcome has been strongly criticized by many authors on theoretical grounds (see references in [181] for an updated discussion). In particular, a radial stability analysis carried out by [22] showed that fully relativistic, corotating binary configurations are stable against collapse to black holes all the way down to the innermost stable circular orbit. More recently Flanagan [70] has pointed out the use of an incorrect form of the momentum constraint equation in the simulations performed by Wilson and collaborators [231, 232], which gives rise to a first post-Newtonian-order error in the scheme, showing analytically that this error can cause the observed increase of the central densities obtained in the simulations. However, in revised hydrodynamical simulations performed by Mathews and Wilson [132], which incorporate the correction identified by Flanagan [70], it was found that the compression effect is not completely eliminated, although its magnitude significantly diminishes at a given angular momentum. Reliable numerical simulations with the full set of Einstein equations will ultimately clarify these results.

Nakamura and co-workers have been pursueing a programme to simulate neutron star binary coalescence in general relativity since the late 0’s (see, e.g., [151]). A three-dimensional code employing the full set of Einstein equations and self-gravitating matter fields has been developed [165]. In this code the complete set of equations, spacetime and hydrodynamics, are finite-differenced on a uniform Cartesian grid using van Leer’s scheme [220] with TVD flux lim-iters. Shock waves are spread out using a tensor artificial viscosity algorithm. The hydrodynamic equations follow Wilson’s formulation and the ADM formalism is adopted for the Einstein equations. This code has been tested by the study of the gravitational collapse of a rotating polytrope to a black hole (comparing to the axisymmetric computation of [212]) and applied to the coalescence of a binary neutron star system. Further work to achieve long term stability is currently under way [165].

The most advanced simulations of neutron star coalescence in full general relativity are those reported recently by Shibata [203, 206]. His code is able to simulate a coalescence event for a long time from the innermost circular orbit up to the formation of a final merged object (either a black hole or a neutron star). The code shares many features with that of Oohara and Nakamura [165]: The hydrodynamic equations are formulated following Wilson’s approach and they are solved using van Leer’s [220] second order finite difference scheme with artificial viscosity. The most important difference concerns the reformulation of the ADM Einstein equations into a conformal traceless system, as mentioned previously. This formulation was originally introduced by Shibata and Nakamura [205] and recently slightly modified by [24]. In [203] Shibata computed the merger of two models of corotating binary neutron stars of Γ = 5/3 in contact and in approximate quasi-equilibrium orbits. The central density of each star in the two models is 6 × 10^-4 (mildly relativistic) and 10^-3 in geometrized units. The quasi-equilibrium models are constructed assuming a polytropic EOS with K = 10. For both initial models, the neutron stars begin to merge forming spiral arms at half the orbital period P of the quasi-equilibrium states, and by t ≈ 1.5P the final object is a rapidly and differentially rotating highly flattened neutron star. For the more relativistic model the central density of the merged object is ≈ 1.4 × 10^-3, which is nearly the maximum allowed density along the sequence of stable neutron stars of K = 10 and Γ = 5/3. Hence, a black hole could be formed directly in the merger of initially more massive neutron stars. For the cases considered by Shibata, the new star is strongly supported by rapid rotation (J/M ²_g ≈ 1, J being the angular momentum and M_g the gravitational mass) and could eventually collapse to a black hole once sufficient angular momentum has dissipated through, e.g., neutrino emission or gravitational radiation.

Recently, Miller et al. [141] have studied the head-on collision of two neutron stars by means of time-dependent relativistic simulations using the code of Font et al. [76]. These simulations are aimed at investigating whether the collapse of the final object occurs in prompt timescales (i.e. a few milliseconds) or delayed (after neutrino cooling) timescales (i.e. a few seconds). In [196] it was argued that in a head-on collision event sufficient thermal pressure is generated to support the remnant in quasi-static equilibrium against (prompt) collapse prior to slow cooling via neutrino emission (delayed collapse). Nevertheless, in [141] prompt collapse to a black hole was found in the head-on collision of two 1.4M_⊙ neutron stars modeled by a polytropic EOS with Γ = 2 and K = 1.16 × 10⁵ cm⁵ g^-1 s^-2. The stars are initially separated by a proper distance of d = 44 km and are boosted towards one another at a speed of $\sqrt {GM/d}$ (the Newtonian infall velocity). The simulation employed a Cartesian grid of 192³ points. The time evolution of this simulation can be followed in the Quicktime movie in Fig. 11. This animation simultaneously shows the rest-mass density and the internal energy evolution during the on-axis collision. The formation of the black hole in prompt timescales is demonstrated by the sudden appearance of the apparent horizon at t = 0.16 ms (t = 63. 194 in code units). The violet dotted circles indicate the trapped photons. The animation also shows a moderately relativistic shock wave (Lorentz factor of about 1.2) appearing at t ≈ 36 (code units; yellow-white colors) which eventually is followed by two opposite moving shocks (along the infalling z direction) which propagate along the atmosphere surrounding the black hole.

Figure 11

mpg-Movie (558 KB) Still from a movie showing the animation of a head-on collision simulation of two 1.4M_⊙ neutron stars obtained with a relativistic code [76, 141]. The movie shows the evolution of the density and internal energy. The formation of the black hole in prompt timescales is demonstrated by the sudden appearance of the apparent horizon at t 0.16 ms (t 63.194 in code units), which is indicated by violet dotted circles representing the trapped photons.(For video see appendix)