Relativistic Binaries in Globular Clusters

Abstract

The galactic population of globular clusters are old, dense star systems, with a typical cluster containing 10⁴ – 10⁶ stars. As an old population of stars, globular clusters contain many collapsed and degenerate objects. As a dense population of stars, globular clusters are the scene of many interesting close dynamical interactions between stars. These dynamical interactions can alter the evolution of individual stars and can produce tight binary systems containing one or two compact objects. In this review, we discuss the theoretical models of globular cluster evolution and binary evolution, techniques for simulating this evolution which lead to relativistic binaries, and current and possible future observational evidence for this population. Globular cluster evolution will focus on the properties that boost the production of hard binary systems and on the tidal interactions of the galaxy with the cluster, which tend to alter the structure of the globular cluster with time. The interaction of the components of hard binary systems alters the evolution of both bodies and can lead to exotic objects. Direct N-body integrations and Fokker-Planck simulations of the evolution of globular clusters that incorporate tidal interactions and lead to predictions of relativistic binary populations are also discussed. We discuss the current observational evidence for cataclysmic variables, millisecond pulsars, and low-mass X-ray binaries as well as possible future detection of relativistic binaries with gravitational radiation.

1 Introduction

Binaries containing white dwarfs, neutron stars, and black holes in compact orbits are over-represented in globular clusters compared with their population in the galactic field. From this population come a host of exotic objects such as ultracompact cataclysmic variables, non-flickering X-ray and UV sources, low-mass X-ray binaries, and millisecond pulsars. These objects and their dark counterparts in the population of relativistic binaries are also likely to be observable sources of gravitational radiation for low-frequency gravitational wave detectors such as the proposed spaceborne interferometer LISA. A relativistic binary is a product of interplay between stellar evolution and the gravitational interaction of a tight binary. The population of tight binaries in globular clusters is a product of the dynamical evolution of an N-body gravitational system. Thus, relativistic binaries result from a combination of several of the more interesting processes in astrophysics. In keeping with the focus of this review article on relativistic binaries in globular clusters, we shall only touch on the aspects of globular clusters, observations, binary evolution, and N-body dynamics as they relate to populations of this specific class of binaries in globular clusters.

We begin by looking at the physical structure and general history of the galactic globular cluster system that leads to the concentration of evolved stars, stellar remnants, and binary systems in the cores of the clusters. Current observations of the cores of globular clusters that have revealed numerous tracer populations of relativistic binaries are also discussed. We also look at the prospects for future observations in this rapidly changing area. Many of these relativistic binaries are the product of stellar evolution in compact binaries. We will look at how mass transfer from one star in the presence of a nearby companion can dramatically alter the evolution of both stars in the process of binary evolution. The enhanced production of relativistic binaries in globular clusters results from dynamical processes that drive binaries toward tighter orbits and that preferentially exchange more massive and degenerate objects into binary systems. Numerical simulations of globular cluster evolution, which can be used to predict the rate at which relativistic binaries are formed, are discussed. These models are compared with the observable members of the population of relativistic binaries. Finally, we conclude with a brief discussion of the prospects for observing these systems in gravitational radiation.

Readers interested in further studies of the structure and evolution of globular clusters are invited to look at Binney and Tremaine [19], Spitzer [152], and Volumes I and II of Padmanabhan’s Theoretical Astrophysics [116, 117] for a good introduction to the physical processes involved. The recent review articles of Meylan and Heggie [107] and Meylan [106] also provide a comprehensive look at the internal dynamics of globular clusters. Although our focus is solely on the galactic globular cluster system, the physics of globular cluster systems associated with other galaxies is well covered in the review article by Harris [67] as well as his lecture notes from the Saas-Fee course on star clusters [69]. Carney has a thorough introduction to evolution of stars in globular clusters [22]. An observational perspective on the role of binaries in globular clusters is presented in an excellent review by Bailyn [11], while a good introduction to the details of observing binary systems in general can be found in An Introduction to Close Binary Stars [74]. Although slightly out of date, the review of binaries in globular clusters by Hut et al. [83] is an excellent introduction to the interaction between globular cluster dynamics and binary evolution. An updated, short article on globular cluster binaries by McMillan, Pryor, and Phinney [105] is also of value. Rappaport et al. [132] and Rasio et al. [133] have written recent reviews of numerical simulations of binary populations in globular clusters. A recent article by Pfahl et al. [121] has an in-depth discussion of the details of the retention of neutron stars in globular clusters.

2 Globular Clusters

Globular clusters comprising 10⁴ to 10⁷ stars were formed early in the history of the Milky Way, and are scattered throughout the halo. The age of the clusters is about 13 Gyr, with an age spread of less than 5 Gyr [23]. According to a frequently updated catalog of globular cluster properties maintained on the web by Harris [68], the globular cluster system numbers roughly 150 clusters. Although the list is fairly complete, two new globular clusters were recently discovered at very low galactic latitudes [81], and there is the prospect for a few more clusters to be hidden behind the bulge or out in the far reaches of the galaxy. The distribution of globular clusters in galacto-centric coordinates is shown in Figure 1.

Figure 1

Globular cluster distribution about the galaxy. Positions are from Harris [68] and are plotted as black circles on top of the COBE FIRAS 2.2 micron map of the Galaxy using a Mollweide projection. Figure taken from Brian Chaboyer’s website [24].

2.1 Globular clusters stars

Because the clusters are of great age, most of the stars above about 0.8M_⊙ have already evolved off the main sequence. Thus, a large number of red giants are readily visible in most pictures of globular clusters (see Figure 2). When viewing the color-magnitude diagram (CMD) for a globular cluster, one can clearly see the red giant branch lifting up away from the main sequence. The horizontal branch of evolved stars is also seen in the CMD for M80 shown in Figure 3.

Figure 2

Hubble Space Telescope photograph of the dense globular cluster M80 (NGC 6093).

Figure 3

Color-magnitude diagram for M80. The diagram on the right focuses on the turn-off of the main sequence and the red giant branch. The diagram on the left indicates a number of different objects. HB indicates the horizontal branch, RGB is the red giant branch, SGB is the subgiant branch, and BSS indicate the blue stragglers. Blue stragglers will be discussed later in this review and the interested reader can consult [46] for a discription of the other objects. Figure taken from Ferraro et al. [46].

That there is a clearly visible turn-off point in the CMD for globular clusters is evidence for the roughly coeval nature of the stars in the cluster. During the early stages of the evolution of a globular cluster, most of the gas and dust has been swept away. Subsequent replenishment of the intercluster gas by stellar winds from evolved stars is removed during periodic passages of the cluster through the plane of the galaxy. The remaining gas is generally too hot for any star formation to take place [49]. Thus globular clusters are made up of old, population II stars.

2.2 Globular cluster structure

The overall structure of a globular cluster can be described in terms of an N-body system. These systems, each containing between 10⁴ and 10⁷ stars, have central densities in the range 10^-1 to 10⁶M_⊙/pc³, with an average of 10⁴M_⊙/pc³. The important characteristic radii of a globular cluster are the core radius r_c, the half-light radius r_h, and the tidal radius r_t. The core radius is defined to be the radius at which the surface brightness has dropped to half the central value. The half-light radius is the radius that contains half of the light of the cluster and the tidal radius is defined as the radius beyond which the external gravitational field of the galaxy dominates the dynamics. Theorists define r_h to be the radius containing half the mass of the cluster. The half-mass radius is a three-dimensional construct, while the half-light radius is two-dimensional. The tidal radius is always determined by some theoretical model. Typical values of these radii are 1.5 pc, 10 pc, and 50 pc, respectively [19, 117].

There are also important characteristic time scales that govern the dynamics of globular clusters. These are the crossing time t_cross, the relaxation time t_relax, and the evaporation time t_evap. The crossing time is the typical time required for a star in the cluster to travel the characteristic size R of the cluster (typically taken to be the half-mass radius). Thus, t_cross∼R/v, where v is a typical velocity (∼10 km/s). The relaxation time is the typical time for gravitational interactions with other stars in the cluster to remove the history of a star’s original velocity. This amounts to the time required for gravitational encounters to alter the star’s velocity by an amount comparable to its original velocity. Since the relaxation time is related to the number and strength of the gravitational encounters of a typical cluster star, it is related to the number of stars in the cluster and the average energy of the stars in the cluster. Thus, it can be shown that the mean relaxation time for a cluster is [19, 116]

$$ {t_{{\rm{relax}}}} \simeq \frac{{0.1N}}{{\ln N}}{t_{{\rm{cross}}}}. $$

((1))

For a globular cluster with N=10⁵, a characteristic size of R∼r_h∼10 pc, and a typical velocity of v∼10 km/s, the crossing time and relaxation time are t_cross∼10⁵ yr and t^relax∼10⁸ yr [19]. It should be noted, however, that Figure 1.3 of Spitzer [152] gives a median t_relax∼1 Gyr and Padmanabhan gives t_relax∼10⁹ yr [117].

The evaporation time for a cluster is the time required for the cluster to dissolve through the gradual loss of stars that gain sufficient velocity through encounters to escape its gravitational potential. In the absence of stellar evolution and tidal interactions with the galaxy, the evaporation time can be estimated by assuming that a fraction γ of the stars in the cluster are evaporated every relaxation time. Thus, the rate of loss is dN/dt=-γN/t_relax=-N/t_evap. The value of γ can be determined by noting that the escape speed v_e at a point x is related to the gravitational potential Ф(x) at that point by v ²_e =-2Ф(x). Consequently, the mean-square escape speed in a cluster with density ρ(x) is

$$ \left\langle {v_{\rm{e}}^2} \right\rangle = \frac{{\int {\rho (x)} v_{\rm{e}}^2{d^3}x}}{{\int {\rho (x)} {d^3}x}} = - 2\frac{{\int {\rho (x)} \Phi (x){d^3}x}}{M} = - \frac{{4W}}{M}, $$

((2))

where W is the total potential energy of the cluster and M is its total mass. If the system is virialized (as we would expect after a relaxation time), then -W=2K=M〈v²〉, where K is the total kinetic energy of the cluster, and

$$ \left\langle {v_{\rm{e}}^2} \right\rangle = 4\left\langle {{v^2}} \right\rangle. $$

((3))

Thus, stars with speeds above twice the RMS speed will evaporate. Assuming a Maxwellian distribution of speeds, the fraction of stars with v>2v_rms is γ=7.38×10^-3. Therefore, the evaporation time is

$$ {t_{{\rm{evap}}}} = \frac{{{t_{{\rm{relax}}}}}}{\gamma } = 136{t_{{\rm{relax}}}}. $$

((4))

Stellar evolution annd tidal interactions tend to shorten the evaporation time. See Gnedin and Ostriker [59] and references therein for a thorough discussion of these effects. For a globular cluster, t_evap∼10¹⁰ yr, which is comparable to the observed age of globular clusters.

The characteristic time scales differ significantly from each other: t_cross《t_relax《t_evap. When discussing stellar interactions during a given epoch of globular cluster evolution, it is possible to describe the background structure of the globular cluster in terms of a static model. These models describe the structure of the cluster in terms of a distribution function f that can be thought of as providing a probability of finding a star at a particular location in phase-space. The static models are valid over time scales which are shorter than the relaxation time so that gravitational interactions do not have time to significantly alter the distribution function. We can therefore assume ∂f/∂t∼0. The structure of the globular cluster is then determined by the collisionless Boltzmann equation,

$$ v \cdot \nabla f - \nabla \phi \cdot \frac{{\partial f}}{{\partial v}} = 0, $$

((5))

where the gravitational potential φ is found from f with

$$ {\nabla ^2}\phi = 4\pi \int {f\left( {x,v,m} \right){d^3}v\;dm.} $$

((6))

The solutions to Equation (5) are often described in terms of the relative energy per unit mass ε≡#x03C8;−v²/2 with the relative potential defined as ψ≡-φ+φ₀. The constant φ₀ is chosen so that there are no stars with relative energy less than 0 (i.e. f>0 for ε>0 and f=0 for ε<0). A simple class of solutions to Equation (5),

$$ f(\varepsilon ) = F{\varepsilon ^{7/2}}, $$

((7))

generate what are known as Plummer models. A convenient class of models which admit anisotropy and a distribution in angular momenta L are known as King-Michie models. The King-Michie distribution function is:

$$ f(\varepsilon ,L) = {\rho _1}{(2\pi {\sigma ^2})^{ - 3/2}}\exp \left( {\frac{{ - {L^2}}}{{2r_{\rm{a}}^2{\sigma ^2}}}} \right)\left[ {{e^{\varepsilon /{\sigma ^2}}} - 1} \right],\;\varepsilon > 0, $$

((8))

with f=0 for ε≤0 and ρ₁ a constant. The velocity dispersion is determined by σ and the anisotropy radius r_a is defined so that the velocity distribution changes from nearly isotropic at the center to nearly radial at r_a.

2.3 Globular cluster evolution

An overview of the evolution of globular clusters can be found in Hut et al. [83], Meylan and Heggie [107], and Meylan [106]. We summarize here the aspects of globular cluster evolution that are relevant to the formation and concentration of relativistic binaries. The formation of globular clusters is not well understood [54] and the details of the initial mass function (IMF) are an ongoing field of star cluster studies. Although the IMF is expected to be flatter at the low-mass end (see [94] for a discussion of the local IMF), many theorists assume an IMF that follows a standard Salpeter form:

$$ dN \propto {m^{ - \alpha }}dm. $$

((9))

Once the stars form out of the initial molecular cloud, the system will undergo violent relaxation as the protocluster first begins to collapse. The effect of this is that the stars are distributed widely in position and velocity, with a distribution that is independent of the stellar mass. Thus, the more massive stars will have more kinetic energy. These stars will then lose their kinetic energy to the less massive stars through stellar encounters, leading towards equipartition of energy. Through virialization, this tends to concentrate the more massive stars in the center of the cluster. The process of mass segregation for stars of mass m_i occurs on a timescale given by t_i∼t_relax〈m〉/m_i.

The higher concentration of stars in the center of the cluster increases the probability of an encounter, which, in turn, decreases the relaxation time. Thus, the relaxation time given in Equation (1) is an average over the whole cluster. The local relaxation time of the cluster is given in Meylan and Heggie [107] and can be described by:

$$ {t_{\rm{r}}} = \frac{{0.065{{\left\langle {{v^2}} \right\rangle }^{3/2}}}}{{\rho \left\langle m \right\rangle {G^2}\ln \Lambda }}, $$

((10))

where ρ is the local mass density, 〈v²〉 is the mass-weighted mean square velocity of the stars, 〈m〉 is the mean stellar mass, and Λ≃0.4N (although a choice of Λ≃0.1N may be more appropriate in the presence of a mass spectrum [57]). Note that in the central regions of the cluster, the value of t_r is much lower than the average relaxation time. This means that in the core of the cluster, where the more massive stars have concentrated, there are more encounters between these stars.

The concentration of massive stars in the core of the cluster will occur within a few relaxation times, t∼t_relax∼10⁹ yr. This time is longer than the lifetime of low metallicity stars with M≥2M⊙ [142]. Consequently, these stars will have evolved into carbon-oxygen (CO) and oxygen-neon (ONe) white dwarfs, neutron stars, and black holes. After a few more relaxation times, the average mass of a star in the globular cluster will be around 0.5M⊙ and these degenerate objects will once again be the more massive objects in the cluster, despite having lost most of their mass during their evolution. Thus, the population in the core of the cluster will be enhanced in degenerate objects. Any binaries in the cluster that have a gravitational binding energy significantly greater than the average kinetic energy of a cluster star will act effectively as single objects with masses equal to their total mass. These objects, too, will segregate to the central regions of the globular cluster [161]. The core will then be overabundant in binaries and degenerate objects.

The core would undergo what is known as core collapse within a few tens of relaxation times unless these binaries release some of their binding energy to the cluster. In core collapse, the central density increases to infinity as the core radius shrinks to zero. An example of core collapse can be seen in the comparison of two cluster evolution simulations shown in Figure 4 [89]. Note the core collapse when the inner radius containing 1% of the total mass dramatically shrinks after t∼15t_relax. Since these evolution syntheses are single-mass, Plummer models without binary interactions, the actual time of core collapse is not representative of a real globular cluster.

Figure 4

Lagrange radii indicating the evolution of a Plummer model globular cluster for an N-body simulation and a Monte Carlo simulation. The radii correspond to radii containing 0.35, 1, 3.5, 5, 7, 10, 14, 20, 30, 40, 50, 60, 70, and 80% of the total mass. Figure taken from Joshi et al. [89].

The static description of the structure of globular clusters using King-Michie or Plummer models provides a framework for describing the environment of relativistic binaries and their pro-genitors in globular clusters. The short-term interactions between stars and degenerate objects can be analyzed in the presence of this background. Over longer time scales (comparable to t_relax), the dynamical evolution of the distribution function as well as population changes due to stellar evolution can alter the overall structure of the globular cluster. We will discuss the dynamical evolution and its impact on relativistic binaries in Section 5.

Before moving on to the dynamical models and population syntheses of relativistic binaries, we will first look at the observational evidence for these objects in globular clusters.

3 Observations

Observations of relativistic binaries in globular clusters are hampered by the fact that most of the binaries have segregated to the cores of the clusters where crowding is a problem. Furthermore, most of these systems are only visible during mass transfer or accretion stages of the evolution. One tracer of the processes that may lead to relativistic binaries is the population of “blue stragglers.” These stars appear on the main sequence to the left of the turn-off in the CMD of a globular cluster (see Figure 3). They are hot and massive enough that they should have already evolved off the main sequence. Blue stragglers are thought to arise from stellar coalescences either through the gradual coalescence of the components of binaries in the cluster or through direct collisions. These objects are some of the most visible and populous evidence of dynamical interactions in globular clusters that lead to the formation of ultracompact binary systems. (See Hut [82] and Bailyn [11] for good reviews of the implications of blue stragglers on the dynamics of globular clusters.)

White dwarfs are generally too cool to have their binary properties readily measured. for example, the binary properties of double degenerate cataclysmic variables of the AM CVn type are determined from observing the hot spot where the accreting matter from the donor dwarf collides with the accretion disk around the accretor (see Warner [162] and references therein). With an expected M_V∼10, these objects would be virtually invisible at globular cluster distances. Searches for cataclysmic variables generally focus on low-luminosity X-ray sources [87, 64, 159] and on ultraviolet-excess stars [62, 93, 103], but these systems are usually a white dwarf accreting from a low mass star. The class of “non-flickerers” which have been detected recently [26, 156] have been explained as He white dwarfs in binaries containing dark CO white dwarfs [41, 65].

Pulsars, although easily seen in radio, are difficult to detect when they occur in hard binaries, due to the Doppler shift of the pulse intervals. Thanks to an improved technique known as an “acceleration search” [108], which assumes a constant acceleration of the pulsar during the observation period, more short orbital period binary pulsars are being discovered [20, 21, 29, 30, 48, 51, 130]. For a good review and description of this technique, see Lorimer [98]. The progenitors of the ultracompact millisecond pulsars are thought to pass through a low-mass X-ray binary (LMXB) phase [37, 64, 131, 134]. These systems are very bright and all of them in the globular cluster system are known. There may, however, be some additional LMXBs that are currently quiescent [64]. In addition, a very recent observation has shown that the LMXB in M15 is, in fact, two bright sources [164].

With the exception of M15 [53, 66], no black holes have been identified in globular clusters. Theoretical predictions of black holes in globular clusters indicate that there may be intermediatemass black holes (M∼10³M_⊙) in as many as ∼20 globular clusters [109], or that stellar mass binary black holes may be generated and subsequently ejected from most globular clusters [127]. If the velocity dispersion in globular clusters follows the same correlation to black hole mass as in galactic bulges, then there may be black holes with masses in the range 1–10³M_⊙ in many globular clusters [169].

Recent observations and catalogs of known binaries are presented in the following sections.

3.1 Cataclysmic variables

Cataclysmic variables (CVs) are white dwarfs accreting matter from a companion. They have been detected in globular clusters through identification of the white dwarf itself or through evidence of the accretion process. White dwarfs managed to avoid detection until recent observations with the Hubble Space Telescope revealed photometric sequences in several globular clusters [27, 26, 119, 135, 137, 136, 156]. Spectral identification of white dwarfs in globular clusters has begun both from the ground with the VLT [110] and in space with the Hubble Space Telescope [26, 41, 156]. With spectral identification, it will be possible to identify those white dwarfs in hard binaries through Doppler shifts in the Hβ line. This approach has promise for detecting a large number of the expected double white dwarf binaries in globular clusters.

Accretion onto the white dwarf may eventually lead to a dwarf nova outburst. Identifications of globular cluster CVs have been made through such outbursts in the cores of M5 [103], 47 Tuc [118], and NGC 6624 [148]. With the exception of V101 in M5 [103], original searches for dwarf novae performed with ground based telescopes proved unsuccessful. This is primarily due to the fact that crowding obscured potential dwarf novae up to several core radii outside the center of the cluster [145, 147]. Since binaries tend to settle into the core, it is not surprising that none were found significantly outside of the core. Subsequent searches using the improved resolution of the Hubble Space Telescope eventually revealed a few dwarf novae close to the cores of selected globular clusters [144, 146, 148].

A more productive approach has been to look for direct evidence of the accretion around the white dwarf. This can be in the form of excess UV emission and strong Hα emission [44, 63, 93] from the accretion disk. This technique has resulted in the discovery of candidate CVs in 47 Tuc [44, 93], M92 [47], NGC 6397 [26, 41, 156], and NGC 6712 [45]. The accretion disk can also be discerned by very soft X-ray emissions. These low luminosity X-ray binaries are characterized by a luminosity L_X<10^34.5 erg/s, which distinguishes them from the low-mass X-ray binaries with L_X > 10³⁶ erg/s. Initial explanations of these objects focused on accreting white dwarfs [10], and a significant fraction of them are probably CVs. However, some of the more energetic sources may be LMXBs in quiescence.

Early searches performed with ROSAT data (which had a detection limit of 10³¹ erg/s) revealed roughly 30 sources in 19 globular clusters [87]. A more recent census of the ROSAT low luminosity X-ray sources, published by Verbunt [159], lists 26 such sources that are probably related to globular clusters. Recent observations with the improved angular resolution of Chandra have begun to uncover numerous low luminosity X-ray candidates for CVs [64, 65, 73, 79]. An attempt to identify an IR counterpart to the LMXB X-ray burster in Liller 1 with Chandra also resulted in the serendipitous discovery of 3 low luminosity X-ray sources [79], which may be quiescent LMXBs. Another probable quiescent LMXB has been observed in NGC 5139 with Chandra [140]. Observations of NGC 6652 have also discovered 3 new low luminosity X-ray sources, two of which may be CVs [73]. The most comprehensive survey of X-ray sources in a globular cluster is that of Grindlay et al. [64], which presents results of high resolution Chandra images of 47 Tuc. In addition to numerous other X-ray sources, they report 13 candidate CVs.

The state of the field at this time is one of rapid change as Chandra results come in and optical counterparts are found for the new X-ray sources. A living catalog of CVs has been created by Downes et al. [39] and may be the best source for confirmed CVs in globular clusters.

3.2 Low-mass X-ray binaries

The X-ray luminosities of low-mass X-ray binaries are in the range L_X∼10³⁶–10³⁸ erg/s. The upper limit is close to the Eddington limit for accretion onto a neutron star, so these systems must contain an accreting neutron star or black hole. All of the LMXBs in globular clusters contain an accreting neutron star as they also exhibit X-ray bursts, indicating thermonuclear flashes on the surface of the neutron star [87]. Compared with ∼100 such systems in the galaxy, there are 13 LMXBs known in globular clusters. The globular cluster system contains roughly 0.1% of the mass of the galaxy and roughly 10% of the LMXBs. Thus, LMXBs are substantially over-represented in globular clusters.

Because these systems are so bright in X-rays, the globular cluster population is completely known — we expect no new LMXBs to be discovered in the globular cluster system (unless more multiple sources are resolved from these 13 sources). The 13 sources are in 12 separate clusters. Three have orbital periods greater than a few hours, four ultracompact systems have measured orbital periods less than 1 hour, and six have undetermined orbital periods. A member of the ultracompact group, 4U 1820-30 (X1820-303) in the globular cluster NGC 6624, has an orbital period of 11 minutes [154]. This is the shortest known orbital period of any binary and most certainly indicates a degenerate companion. The orbital period, X-ray luminosity, and host globular clusters for these systems are given in Table 1.

Table 1 Low-mass X-ray binaries in globular clusters. Host clusters and LMXB properties.

The improved resolution of Chandra allows for the possibility of identifying optical counter-parts to LMXBs. If an optical counterpart can be found, a number of additional properties and constraints for these objects can be determined through observations in other wavelengths. In particular, the orbital parameters and the nature of the secondary can be determined. So far, optical counterparts have been found for X0512-401 in NGC 1851 [78], X1745-203 in NGC 6440 [160], X1746-370 in NGC 6441 [36], X1830-303 in NGC 6624 [92], X1832-330 in NGC 6652 [37, 73], X1850-087 in NGC 6712 [28, 12, 115], and X2127+199 in NGC 7078 [9]. Continued X-ray observations will also further elucidate the nature of these systems [111].

Recent observations with Chandra of 47 Tuc [64] and NGC 6397 [65] have revealed quiescent LMXBs which also harbor neutron stars in binaries and are detected by the thermal emission from the neutron star. Work is ongoing, and new developments can be expected in the next few years.

3.3 Millisecond pulsars

The population of known millisecond pulsars (MSPs) seems to be one of the fastest growing populations of relativistic binaries in globular clusters. In the past few years, improved searching techniques have revealed 47 pulsars in globular clusters [98]. The lion’s share of these are in 47 Tuc, with 20 — nine of which were recently discovered with the Parkes radio telescope [20]. Additional recent discoveries have been made in NGC 6544 [29, 30, 130], NGC 6266, NGC 6397, and NGC 6752 [29, 30].

An approach by Fruchter and Goss [51] uses deep multifrequency imaging to estimate the population of pulsars in globular clusters. In this approach, the expected number of pulsars beaming toward the earth, N_puls, is determined by the total radio luminosity observed when the radio beam width is comparable in diameter to the core of the cluster. If the minimum pulsar luminosity is L_min and the total luminosity observed is L_tot, then, with simple assumptions on the neutron star luminosity function,

$$ {N_{{\rm{puls}}}} = \frac{{{L_{{\rm{tot}}}}}}{{{L_{\min }}\ln ({L_{{\rm{tot}}}}/{L_{\min }}}}. $$

((11))

In their observations of 7 globular clusters, Fruchter and Goss have recovered previously known pulsars in NGC 6440, NGC 6539, NGC 6624, and 47 Tuc [51]. Their estimates based on Equation (11) give evidence of a population of between 60 and 200 previously unknown pulsars in Terzan 5, and about 15 each in Liller 1 and NGC 6544 [51].

Chandra imaging of 47 Tuc has also recovered those 15 MSPs with precise radio positions [64]. One of these has now been identified with an optical counterpart that is almost certainly a He white dwarf [40]. The X-ray spectral and temporal characteristics of these suggest that over 50 of the 108 X-ray sources identified in 47 Tuc are millisecond pulsars [64].

To obtain a full understanding of the nature of millisecond pulsars, it is necessary to develop full timing solutions so that the orbits can be determined. Work has begun on the MSPs in 47 Tuc, and Freire et al. [48] have obtained timing solutions for 15 of the known pulsars, including 8 binary systems. The properties of all the globular cluster MSPs with orbital periods less than 1 day are given in Table 2, which is a subset of Table 5 in Lorimer [98].

Table 2 Short orbital period binary millisecond pulsars in globular

With the ongoing Parkes multi-beam surveys of globular clusters and the use of the acceleration technique [98, 108], the population of known MSPs will be expected to grow dramatically in the next few years. This will help improve the understanding of these objects and their progenitors as well as the dynamics of globular clusters.

3.4 Black holes

There have been very few observations of black hole binaries in globular clusters. Although there have been hints of possible black hole binaries in extragalactic globular cluster systems [7, 38], there are no known black hole binaries in the galactic globular cluster system. All of the globular cluster LMXBs exhibit the X-ray variability that is indicative of nuclear burning on the surface of a neutron star. Possible evidence of black holes in globular clusters can be found by extrapolating the velocity dispersion-black hole mass relation for galaxies with bulges to globular clusters. Using velocity dispersion data for 22 galactic globular clusters, Zheng [169] finds possible black hole masses in the range of 1 – 1000M_⊙. Although this is pure speculation, it does provide some indirect suggestion of possible black hole binaries in globular clusters.

4 Relativistic Binaries

Relativistic binaries are binary systems with at least one degenerate or collapsed object and an orbital period such that they will be brought into contact within a Hubble time. (Note that this definition also includes binaries which are already in contact.) Outside of dense stellar clusters, most relativistic binary systems arise from primordial binary systems whose evolution drives them to tight, ultracompact orbits. The dynamical processes in globular clusters can drive wide binary systems toward short orbital periods and can also insert degenerate or collapsed stars into relativistic orbits with other stars. Before addressing specific evolutionary scenarios, we will present the generic features of binary evolution that lead to the formation of relativistic binaries.

4.1 Binary evolution

The evolution of a binary system of two main-sequence stars can significantly affect the evolution of both component stars if the orbital separation is sufficiently small. If the orbital period is less than about 10 days, tidal interactions will have circularized the orbit during the pre- and early main-sequence phase. [60, 167, 168] Both stars start in the main sequence with the mass of the primary M_p, and the mass of the secondary M_s, defined such that M_p≥M_s. The binary system is described by the orbital separation a, and the mass ratio of the components q≡M_s/M_p. The gravitational potential of the binary system is described by the Roche model where each star dominates the gravitational potential inside regions called Roche lobes. The two Roche lobes meet at the inner Lagrange point along the line joining the two stars. Figure 5 shows equipotential surfaces in the orbital plane for a binary with q=0.4. If either star fills its Roche lobe, matter will stream from the Roche lobe filling star through the inner Lagrange point to the other star in a process known as Roche lobe overflow (RLOF). This mass transfer affects both the evolution of the components of the binary as well as the binary properties such as orbital period and eccentricity.

Figure 5

Cross section of equipotential surfaces in the orbital plane of a binary with q=0.4. The values of the potential surfaces are 5.0, 3.9075, 3.8, 3.559, 3.2, 3.0, and 2.8. The units have been normalized to the orbital separation, so a=1.

Roche lobe overflow can be triggered by the evolution of the binary properties or by evolution of the component stars. On the one hand, the orbital separation of the binary can change so that the Roche lobe can shrink to within the surface of one of the stars. On the other hand, stellar evolution may eventually cause one of the stars to expand to fill its Roche lobe. When both stars in the binary are main-sequence stars, the latter process is more common. Since the more massive star will evolve first, it will be the first to expand and fill its Roche lobe. At this stage, the mass exchange can be conservative (no mass is lost from the binary) or non-conservative (mass is lost). Depending on the details of the mass exchange and the evolutionary stage of the mass-losing star there are several outcomes that will lead to the formation of a relativistic binary. The primary star can lose its envelope, revealing its degenerate core as either a helium, carbon-oxygen, or oxygenneon white dwarf; it can explode as a supernova, leaving behind a neutron star or a black hole; or it can simply lose mass to the secondary so that they change roles. Barring disruption of the binary, its evolution will then continue. In most outcomes, the secondary is now the more massive of the two stars and it may evolve off the main sequence to fill its Roche lobe. The secondary can then initiate mass transfer or mass loss with the result that the secondary also can become a white dwarf, neutron star, or black hole.

The relativistic binaries that result from this process fall into a number of observable categories. A WD-MS or WD-WD binary may eventually become a cataclysmic variable once the white dwarf begins to accrete material from its companion. If the companion is a main-sequence star, RLOF can be triggered by the evolution of the companion. If the companion is another white dwarf, then RLOF is triggered by the gradual shrinking of the orbit through the emission of gravitational radiation. WD-WD cataclysmic variables are also known as AM CVn stars. If the total mass of the WD-WD binary is above the Chandrasekhar mass, the system may be a progenitor to a type I supernova.

The orbit of a NS-MS or NS-WD binary will shrink due to the emission of gravitational radiation. At the onset of RLOF, the binary will become either a low-mass X-ray binary (if the donor star is a WD or MS with M≤2M_⊙), or a high-mass X-ray binary (if the donor is a more massive main-sequence star). These objects may further evolve to become millisecond pulsars if the NS is spun up during the X-ray binary phase [34, 134]. A NS-NS binary will remain virtually invisible unless one of the neutron stars is observable as a pulsar. A BH-MS or BH-WD binary may also become a low- or high-mass X-ray binary. If the neutron star is observable as a pulsar, a BH-NS binary will appear as a binary pulsar. BH-BH binaries will be invisible unless they accrete matter from the interstellar medium. A comprehensive table of close binary types that can be observed in electromagnetic radiation can be found in Hilditch [74].

The type of binary that emerges depends upon the orbital separation and the masses of the component stars. During the evolution of a 10M_⊙ star, the radius will slowly increase by a factor of about two as the star progresses from zero age main sequence to terminal age main sequence. The radius will then increase by about another factor of 50 as the star transitions to the red giant phase, and an additional factor of 10 during the transition to the red supergiant phase. These last two increases in size occur very quickly compared with the slow increase during the main-sequence evolution. Depending upon the orbital separation, the onset of RLOF can occur any time during the evolution of the star. Mass transfer can be divided into three cases related to the timing of the onset of RLOF.

• Case A: If the orbital separation is small enough (usually a few days), the star can fill its Roche lobe during its slow expansion through the main-sequence phase while still burning hydrogen in its core.

• Case B: If the orbital period is less than about 100 days, but longer than a few days, the star will fill its Roche lobe during the rapid expansion to a red giant with a helium core. If the helium core ignites during this phase and the transfer is interrupted, the mass transfer is case BB.

• Case C: If the orbital period is above 100 days, the star can evolve to the red supergiant phase before it fills its Roche lobe. In this case, the star may have a CO or ONe core.

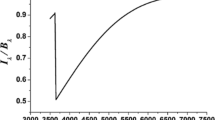
The typical evolution of the radius for a low metallicity star is shown in Figure 6. Case A mass transfer occurs during the slow growth, case B during the first rapid expansion, and case C during the final expansion phase. The nature of the remnant depends upon the state of the primary during the onset of RLOF and the orbital properties of the resultant binary depend upon the details of the mass transfer.

Figure 6

Evolution of the radius for a 10M_⊙ star with Z=0.001. Figure taken from Pfahl et al. [121].

4.2 Mass transfer

Although there are still many unanswered theoretical questions about the nature of the mass transfer phase, the basic properties of the evolution of a binary due to mass transfer can easily be described. The rate at which a star can adjust to changes in its mass is governed by three time scales. The dynamical time scale results from the adiabatic response of the star to restore hydrostatic equilibrium, and can be approximated by the free fall time across the radius of the star

$$ {t_{{\rm{dyn}}}} \simeq {\left( {\frac{{2{R^3}}}{{GM}}} \right)^{1/2}} \sim 40{\left[ {{{\left( {\frac{R}{{{R_ \odot }}}} \right)}^3}\frac{{{M_ \odot }}}{M}} \right]^{1/2}}\min, $$

((12))

where M and R are the mass and radius of the star. The thermal equilibrium of the star is restored over a longer period given by the thermal time scale

$$ {t_{{\rm{th}}}} \simeq \frac{{G{M^2}}}{{RL}} \sim 3 \times {10^7}{\left( {\frac{M}{{{M_ \odot }}}} \right)^2}\frac{{{R_ \odot }}}{R}\frac{{{L_ \odot }}}{L}{\rm{yr,}} $$

((13))

where L is the luminosity of the star. Finally, the main-sequence lifetime of the star itself provides a third time scale, which is also known as the nuclear time scale:

$$ {t_{{\rm{nuc}}}} \sim 7 \times {10^9}\frac{M}{{{M_ \odot }}}\frac{{{L_ \odot }}}{L}{\rm{yr}}{\rm{.}} $$

((14))

The rate of mass transfer/loss from the Roche lobe filling star is governed by how the star’s radius changes in response to changes in its mass. Hjellming and Webbink [77] describe these changes and the response of the Roche lobe to mass changes in the binary using the radius-mass exponents, ζ≡dlnR/dlnM, for each of the three processes described in Equations (12, 13, 14) and defining

$$ {\zeta _{\rm{L}}} = (1 + q)\frac{{d\ln {R_{\rm{L}}}}}{{d\ln q}} $$

((15))

for the Roche lobe radius-mass exponent. If ζ_L>ζ_dyn, the star cannot adjust to the Roche lobe, then the mass transfer takes place on a dynamical time scale and is limited only by the rate at which material can stream through the inner Lagrange point. If ζ_dyn>ζ_L>ζ_th, then the mass transfer rate is governed by the slow expansion of the star as it relaxes toward thermal equilibrium, and it occurs on a thermal time scale. If both ζ_dyn and ζ_th are greater than ζ_L, then the mass loss is driven either by stellar evolution processes or by the gradual shrinkage of the orbit due to the emission of gravitational radiation. The time scale for both of these processes is comparable to the nuclear time scale. A good analysis of mass transfer in cataclysmic variables can be found in King et al. [91].

Conservative mass transfer occurs when there is no mass loss from the system. During conservative mass transfer, the orbital elements of the binary can change. Consider a system with total mass M=M₁+M₂ and semi-major axis a. The total orbital angular momentum

$$ J = {\left[ {\frac{{GM_1^2M_2^2a}}{M}} \right]^{1/2}} $$

((16))

is a constant, and we can write a∝(M₁M₂)^-2. Using Kepler’s third law and denoting the initial values by a subscript i, we find:

$$ \frac{P}{{{P_i}}} = {\left[ {\frac{{{M_{1i}}{M_{2i}}}}{{{M_1}{M_2}}}} \right]^3}. $$

((17))

Differentiating Equation (17) and noting that conservative mass transfer requires Ṁ₁=-Ṁ₂ gives:

$$ \frac{{\dot P}}{P} = \frac{{3{{\dot M}_1}({M_1} - {M_2})}}{{{M_1}{M_2}}}. $$

((18))

Note that if the more massive star loses mass, then the orbital period decreases and the orbit shrinks. If the less massive star is the donor, then the orbit expands. Usually, the initial phase of RLOF takes place as the more massive star evolves. As a consequence, the orbit of the binary will shrink, driving the binary to a more compact orbit.

In non-conservative mass transfer, both mass and angular momentum can be removed from the system. There are two basic non-conservative processes which are important to the formation of relativistic binaries — the common-envelope process and the supernova explosion of one component of the binary. The result of the first process is often a short-period, circularized binary containing a white dwarf. Although the most common outcome of the second process is the disruption of the binary, occasionally this process will result in an eccentric binary containing a neutron star.

Common envelope scenarios result when one component of the binary expands so rapidly that the mass transfer is unstable and the companion becomes engulfed by the donor star. The companion then ejects the envelope of the donor star. The energy required to eject the envelope comes from the orbital energy of the binary and thus the orbit shrinks. The efficiency of this process determines the final orbital period after the common envelope phase. This is described by the efficiency parameter

$$ {\alpha _{{\rm{CE}}}} = \frac{{\Delta {E_{{\rm{bind}}}}}}{{\Delta {E_{{\rm{orb}}}}}}, $$

((19))

where ΔE_bind is the binding energy of the mass stripped from the envelope and ΔE_orb is the change in the orbital energy of the binary. The result of the process is the exposed degenerate core of the donor star in a tight, circular orbit with the companion. This process can result in a double degenerate binary if the process is repeated twice or if the companion has already evolved to a white dwarf through some other process. A brief description of the process is outlined by Webbink [163], and a discussion of the factors involved in determining α_CE is presented in Sandquist et al. [141].

The effect on a binary of mass loss due to a supernova can be quite drastic. Following Padmanabhan [117], this process is outlined using the example of a binary in a circular orbit with radius a. Let v be the velocity of one component of the binary relative to the other component. The initial energy of the binary is given by

$$ E = \frac{1}{2}\left( {\frac{{{M_1}{M_2}}}{{{M_1} + {M_2}}}} \right){v^2} - \frac{{G{M_1}{M_2}}}{a} = - \frac{{G{M_1}{M_2}}}{{2a}}. $$

((20))

Following the supernova explosion of M₁, the expanding mass shell will quickly cross the orbit of M₂, decreasing the gravitational force acting on the secondary. The new energy of the binary is then

$$ E' = \frac{1}{2}\frac{{{M_{{\rm{NS}}}}{M_2}}}{{{M_{{\rm{NS}}}} + {M_2}}}{v^2} - \frac{{G{M_{{\rm{NS}}}}{M_2}}}{a}, $$

((21))

where M_NS is the mass of the remnant neutron star. We have assumed here that the passage of the mass shell by the secondary has negligible effect on its velocity (a safe assumption, see Pfahl et al. [121] for a discussion), and that the primary has received no kick from the supernova (not necessarily a safe assumption, but see Davies and Hansen [34] for an application to globular cluster binaries). Since we have assumed that the instantaneous velocities of both components have not been affected, we can replace them by v²=G(M₁+M₂)/a, and so

$$ E' = \frac{{G{M_{{\rm{NS}}}}{M_2}}}{{2a}}\left( {\frac{{{M_1} + {M_2}}}{{{M_{{\rm{NS}}}} + {M_2}}} - 2} \right). $$

((22))

Note that the final energy will be positive and the binary will be disrupted if M_NS<(1/2)(M₁+M₂). This condition occurs when the mass ejected from the system is greater than half of the initial total mass:

$$ \Delta M > \frac{1}{2}\left( {{M_1} + {M_2}} \right), $$

((23))

where ΔM=M₁−M_NS. If the binary is not disrupted, the new orbit becomes eccentric and expands to a new semi-major axis given by

$$ a' = a\left( {\frac{{{M_1} + {M_2} - \Delta M}}{{{M_1} + {M_2} - 2\Delta M}}} \right), $$

((24))

and orbital period

$$ P' = P{\left( {\frac{{a'}}{a}} \right)^{3/2}}{\left( {\frac{{2a' - a}}{{a'}}} \right)^{1/2}}. $$

((25))

We have seen that conservative mass transfer can result in a tighter binary if the more massive star is the donor. Non-conservative mass transfer can also drive the components of a binary together during a common envelope phase when mass and angular momentum are lost from the system. Direct mass loss through a supernova explosion can also alter the properties of a binary, but this process generally drives the system toward larger orbital separation and can disrupt the binary entirely. With this exception, the important result of all of these processes is the generation of tight binaries with at least one degenerate object.

The processes discussed so far apply for the generation of relativistic binaries anywhere. They occur whenever the orbital separation of a progenitor binary is sufficiently small to allow for mass transfer or common envelope evolution. Population distributions for relativistic binaries are derived from an initial mass function, a distribution in mass ratios, and a distribution in binary separations. These initial distributions are then fed into models for binary evolution in order to determine rates of production of relativistic binaries. The evolution of the binary is often determined by the application of some simple operational formulae such as those described by Tout et al. [158]. for example, Hils, Bender, and Webbink [76] estimated a population of close white dwarf binaries in the disk of the galaxy using a Salpeter mass function, a mass ratio distribution strongly peaked at 1, and a separation distribution that was flat in ln(a). Other estimates of relativistic binaries differ mostly by using different distributions [14, 86, 113, 112].

4.3 Globular cluster processes

When the above evolutionary scenarios are played out in the environment of a globular cluster, additional mechanisms arise that enhance the production of relativistic binaries. New binary systems can be formed by dynamical interaction among three or more single stars or through tidal capture, while the period distribution and binary components of existing binary systems can be altered by interactions with other stars in the cluster. We will discuss here the broad features of these interactions and how they affect the evolution of binary systems toward relativistic binaries.

The formation of binaries during the dynamical evolution of globular clusters can occur either through tidal capture or through N-body interactions. Tidal capture occurs when an encounter between two stars is close enough that significant tides are raised on each. The tides excite non-radial oscillations in the stars. If the energy absorbed in these oscillations is great enough to leave the two stars with negative total energy, then the system will form a binary. This process was originally thought to be the dominant channel through which binaries were formed in globular clusters [19, 43]. It is now thought to be quite rare, as detailed calculations have shown that the final result is more likely to be coalescence of the two stars [11, 83, 134]. Although N-body interactions are less likely to occur than tidally significant two-body interactions, they are now thought to be the dominant channel for the formation of binaries during the evolution of a globular cluster. This process, however, is not likely to produce more than a few binaries during the lifetime of a cluster [19, 117].

The existence of a population of primordial binaries provides a much more efficient channel for the transformation of the initial distribution in component masses and orbital periods towards higher mass components and shorter orbital periods. This process follows from the interaction of primordial binaries with single stars and other binaries. Three results of the interaction are possible: complete disruption of the binary, an exchange of energy between the binary and the field star, or a replacement of one of the binary components by the field star. When a binary interacts with either a field star or with another binary, the energy of the interaction is shared among all stars in the interaction. The result is that the lowest mass object in the interaction will receive the largest velocity and be more likely to escape the interaction. In general, these interactions are quite complex, and must be studied numerically. A typical exchange interaction between a binary and a field star is shown in Figure 7.

Figure 7

Example of a binary-field star exchange interaction. The binary comes in from the right (red-white), while the field star (green) enters from the left. After a complicated interaction, the white star is ejected and the newly formed red-green binary is in a more tightly bound orbit. Figure taken from McMillan [104].

If the initial binding energy of the binary is large, the result of these interactions is to shrink the orbit of the new binary as the gravitational energy of the binary is used to bring the field star up to the speeds of the binary components. However, if the binding energy is low, the field star contributes energy to the components of the binary, thereby widening the orbit. This is an example of “Heggie’s Law” [70], which can be summarized as hard binaries get harder and soft binaries get softer. For roughly equal mass stars, a binary is considered “hard” if its binding energy is greater than the average kinetic energy of a field star in the cluster and “soft” if its binding energy is less. For unequal mass encounters, Hills [75] has shown that the ratio of the orbital speeds of the binary components to the speed of the impactor is a better indicator of whether the binding energy will increase or decrease.

The average kinetic energy of a field star in the cluster is sometimes related to an effective temperature of the cluster [70, 105, 127] so that 〈mv²〉=3kT. Numerical studies of the outcome of hard binary interactions indicate that the binding energy of the binary will increase by about 20% with each encounter [85, 127]. Since the encounter rate is proportional to the semi-major axis (or 1/E) and the energy increase per encounter is proportional to E, the rate of hardening per relaxation time is independent of the energy and is 〈ΔE_bindi〉∼-0.6kT/t_relax [19]. A common feature of numerical studies of hard binary interactions is the preferential exchange of high-mass stars and stellar remnants with the least massive member of the binary [151]. Thus, the dynamical interactions in a globular cluster drive the initial orbital period distribution toward shorter periods by hardening the short period binaries while disrupting the softer binaries. Through exchange interactions, the mass distribution of the binary components is also driven toward higher mass stars, which further enhances the number of mass-transferring systems that can evolve to become relativistic binaries.

Because stellar remnants can also be exchanged into hard binaries, globular cluster evolution opens up a new channel for the formation of relativistic binaries by introducing evolved components into binary systems that have not yet undergone a mass transfer phase. A particularly promising channel involves the exchange of a neutron star into a binary with a main-sequence star. The binary then undergoes case B or case C mass transfer with a common envelope phase, resulting in a NS-WD binary [134]. Podsiadlowski et al. describe a similar process without requiring the common envelope phase [123]. Similar interactions can occur to produce WD-WD binaries if a massive CO or ONe white dwarf is exchanged into a hard binary.

Black hole binaries can also form as a result of exchange interactions, but the process is different because black hole progenitors will evolve so quickly in relation to the relaxation time of most globular clusters [96, 150]. One scenario that generates black hole binaries in globular clusters is described by Portegies Zwart and McMillan [127]. Stellar mass black holes of mass M∼10M_⊙ will be born early in the life of a globular cluster and, through mass segregation, they will quickly sink to the core. Once in the core, these black holes will be so much more massive than the field stars that they will effectively form their own cluster and interact solely with themselves. Single black holes will form binaries with other black holes through three-body encounters; any black holes which are in binaries with other stars will team up with another black hole through exchange encounters. This population of black holes and black hole binaries will then evolve separately from the rest of the cluster as no other stars will be massive enough to affect its dynamics.

We have seen how the dynamics of globular clusters can enhance the population of progenitors to relativistic binaries, making the standard channels of mass-transfer more likely to occur. In addition, globular cluster dynamics can open up new channels for the formation of relativistic binaries by inserting evolved, stellar remnants such as neutron stars or white dwarfs into binary systems and by shrinking the orbits of binary systems to enhance the likelihood of mass exchange. Finally, binary-single star encounters can simply create relativistic binaries by inserting two evolved objects into a binary and then shrinking the orbit to ultracompact periods. We next discuss the probable rates for the formation of such systems and the dynamical simulations that are used to synthesize globular cluster populations of relativistic binaries.

5 Dynamical Evolution

Simulations of the populations of relativistic binaries in globular clusters rely on the interplay between the evolution of individual stars in the progenitor systems and the evolution of globular clusters. The evolution of stars in the progenitor systems has been discussed in the previous section and we now turn to techniques for simulating the evolution of globular clusters.

The evolution of a globular cluster is dominated by the gravitational interaction between the component stars in the cluster. The overall structure of the cluster as well as the dynamics of most of the stars in the cluster are determined by simple N-body gravitational dynamics. However, the evolutionary time scales of stellar evolution are comparable to the relaxation time and core collapse time of the cluster. Consequently, stellar evolution affects the masses of the component stars of the cluster, which affects the dynamical state of the cluster. Thus, the dynamical evolution of the cluster is coupled to the evolutionary state of the stars. Also, as we have seen in the previous section, stellar evolution governs the state of the binary evolution and binaries provide a means of support against core collapse. Thus, the details of binary evolution as coupled with stellar evolution must also be incorporated into any realistic model of the dynamical evolution of globular clusters. To close the loop, the dynamical evolution of the globular cluster affects the distribution and population of the binary systems in the cluster. In our case, we are interested in the end products of binary evolution, which are tied both to stellar evolution and to the dynamical evolution of the globular cluster. To synthesize the population of relativistic binaries, we need to look at the dynamical evolution of the globular cluster as well as the evolution of the binaries in the cluster.

General approaches to this problem involve solving the N-body problem for the component stars in the cluster and introducing binary and stellar evolution when appropriate to modify the N-body evolution. There are two fundamental approaches to tackling this problem — direct integration of the equations of motion for all N bodies in the system and large-N techniques, such as Fokker-Planck approximations coupled with Monte Carlo treatments of binaries (see Heggie et al. [71] for a comparison of these techniques). In the next two subsections, we discuss the basics of each approach and their successes and shortfalls. We conclude this section with a discussion of the recent relativistic binary population syntheses generated by dynamical simulations.

5.1 N-body

The N-body approach to modeling globular cluster dynamics involves direct calculations of the gravitational interactions between all N bodies in the simulation. In principle this is a very straightforward approach. The positions of the N objects in the cluster are determined by direct integration of the 3N equations of motion:

$$ {{\rm{\ddot r}}_i} = - \sum\limits_{j \ne i} {\frac{{G{M_j}\left( {{{\rm{r}}_i} - {{\rm{r}}_j}} \right)}}{{{{\left| {{{\rm{r}}_j} - {{\rm{r}}_i}} \right|}^3}}}.} $$

((26))

When the positions indicate that objects are sufficiently close to each other, then the interaction is modeled to determine the outcome. In order to achieve realistic simulations with tidal interactions, possible mass transfer, and a mass spectrum of bodies, detailed stellar evolution and stellar collision models must be included and calculated.

The two main codes for performing N-body simulations are Kira and NBODYx. The Kira integrator is part of the Starlab environment which also includes stellar evolution codes and other modules for doing N-body simulations [84]. The NBODYx codes have been developed and improved by Aarseth since the early 1960’s. He has two excellent summmaries of the general properties and development of the NBODYx codes [4, 3]. A good summmary of general N-body applications can also be found at the NEMO website [157]. Most large N-body calculations are done with a special purpose computer called the GRAPE (GRAvity PipE) invented by Makino [102]. The most recent incarnation of the GRAPE is the GRAPE 6, which has a theoretical peak speed of 100 Tflops [1]. The GRAPE calculates the accelerations and jerks for the interaction between each star in the cluster.

The main advantage of N-body simulations is the small number of simplifying assumptions which must be made concerning the dynamical interactions within the cluster. The specific stars and trajectories involved in any interactions during the simulation are known. Therefore, the details for those specific interactions can be calculated during the simulation. Within the limits of the numerical errors that accumulate during the calculation [61], one can have great confidence in the results of N-body simulations.

Obviously, one of the main computational difficulties is simply the CPU cost necessary to integrate the equations of motion for N bodies. This scales roughly as N³ [72]. The other computational difficulty of the direct N-body method is the wide range of precision required [82, 72]. Consider the range of distances, from the size of neutron stars (∼10 km) to the size of the globular cluster (∼50 pc ∼10¹⁵ km), spanning 14 orders of magnitude. If the intent of the calculations is to determine the frequency of interactions with neutron stars, we have to know the relative position of every star to within 1 part in 10¹⁴. The range of time scales is worse yet. Considering that the time for a close passage of two neutron stars is on the order of milliseconds and that the age of a globular cluster is 10¹⁰ yr ∼10²⁰ ms, we find that the time scales span 20 orders of magnitude. These computational requirements coupled with hardware limitations mean that the number of bodies which can be included in a reasonable simulation is no more than ∼10⁵. This is about an order of magnitude less than the number of stars in a typical globular cluster.

Although one has great confidence in the results of an N-body simulation, these simulations are generally for systems that are smaller than globular clusters. Consequently, applications of N-body simulations to globular cluster dynamics involve scaling lower N simulations up to the globular cluster regime. Although many processes scale with N, they do so in different ways. Thus, one scales the results of an N-body simulation based upon the assumption of a dominant process. However, one can never be certain that the extrapolation is smooth and that there are no critical points in the scaling with N. One can also scale other quantities in the model, so that the quantity of interest is correctly scaled [126]. An understanding of the nature of the scaling is crucial to understanding the applicability of N-body simulations to globular cluster dynamics (see Baumgardt [13] for an example). The scaling problem is one of the fundamental shortcomings of the N-body approach.

5.2 Fokker-Planck

The computational limitations of N-body simulations can be sidestepped by describing the system in terms of distribution functions f_m(x, v, t) with the number of stars of mass m at time t in the range (x, x+d³x) and (v, v+d³v) given by dN=f_md³xd³v. This description requires that either the phase-space element d³xd³v be small enough to be infinitesimal yet large enough to be statistically meaningful, or that f_m be interpreted as the probability distribution for finding a star of mass m at a location in phase space. The evolution of the cluster is then described by the evolution of f_m. The gravitational interaction is provided by a smoothed gravitational potential φ, which is determined by

$$ {\nabla ^2}\phi = 4\pi \sum\limits_i {\left[ {{m_i}\int {{f_{{m_i}}}\left( {{\rm{x,v,}}t} \right){d^3}v} } \right].} $$

((27))

The effect of gravitational interactions is modeled by a collision term Г[f] (see [19, 117] for specific descriptions of Г). The dynamics of the globular cluster are then governed by the Fokker-Planck equation:

$$ \frac{{\partial f}}{{\partial t}} + {\rm{v}} \cdot \nabla f - \nabla \phi \cdot \frac{{\partial f}}{{\partial {\rm{v}}}} = \Gamma \left[ f \right]. $$

((28))

In the Fokker-Planck approach, the mass spectrum of stars is binned, with a separate f_m for each bin. Increasing the resolution of the mass spectrum requires increasing the number of distribution functions and thus increasing the complexity of the problem. The inclusion of additional physical variables such as binaries adds further complexity. Methods for numerically solving the Fokker-Planck equation use either an orbit-averaged form of Equation (28) [25], or a Monte Carlo approach [50, 55, 56, 89].

The two time scales involved in the evolution of f_m are t_cross (which governs changes in position) and t_relax (which governs changes in energy). The orbit-averaged form of Equation (28) derives from the realization that changes in position are essentially periodic with orbital period T∼t_cross《t_relax. Thus, one can average over the rapid changes in position and retain the slow changes in the phase space coordinates that occur over relaxation times. When one does this, the Fokker-Planck equation is reduced to an equation involving three phase-space variables and time. The most appropriate variables are the energy and angular momentum. The orbit-averaged solutions of the Fokker-Planck equation cannot easily handle the effect of binaries and the binary interactions that occur during the evolution of a globular cluster [52]. These effects are usually inserted by hand using statistical methods. The advantages of the orbit-averaged approach are that one can generalize it to handle anisotropy in velocity, thus allowing study of the effects of the galactic gravitational field and tidal stripping. One can also include the rotation of the cluster [90].

Monte Carlo simulations do not actually solve the Fokker-Planck equation, but rather rely on a representative sample of n test stars which are followed numerically with random velocity perturbations applied as are appropriate to the diffusion coefficients in Г. The advantage of the Monte Carlo approach is that one can handle binary interactions and stellar evolution directly (and then extrapolate the results of the n test stars to the N actual stars in the cluster). However, like Fokker-Planck, the Monte Carlo method currently requires the cluster to be spherically symmetric, so gravitational effects of the galaxy must be treated in an ad hoc way.

5.3 Population syntheses

There have been several recent works addressing binary populations in globular clusters [16, 18, 33, 31, 32, 34, 109, 121, 124, 127, 132, 134, 143, 151, 155]. These have been derived from both dynamical simulations and static models. Although the motivations have been varied, it is often possible to extract information about the resulting populations of relativistic binaries. Despite the differing models and population synthesis techniques, the predicted populations are in rough agreement. Here, we summarize the different techniques and their predictions for relativistic binaries in globular clusters.

5.3.1 N-body simulations

Although N-body simulations have the potential to provide the most detailed population syntheses of relativistic binaries in globular clusters, there are very few actual populations described in the literature. Most of the current work that treats binaries in a consistent and detailed way is limited to open clusters [128, 80, 95] and is focused on a particular outcome of the binary population, such as blue stragglers in the case of Hurley et al. [80], or brown dwarfs in the case of Kroupa et al. [95]. Portegies Zwart et al. focus on photometric observations of open clusters, but promise a more detailed look at the binary population in a future spectroscopic paper [128]. In their comparison of N-body and Fokker-Planck simulations of the evolution of globular clusters, Takahashi and Portegies Zwart [155] followed the evolution of N=1 K, 16 K, and 32 K systems with initial mass functions given by Equation (9) and initial density profiles set up from King models. Although they allowed for realistic stellar binary evolution in their comparisons, their focus was on the structural evolution of globular clusters. Consequently there is no binary population provided. Other N-body simulations suffer from this same problem [125].

It is possible to generate a population distribution for black hole binaries in globular clusters using the N-body simulations of Portegies Zwart and McMillan [127] that were intended to describe the population of black hole binaries that were ejected from globular clusters. Their scenario for black hole binary ejection describes a population of massive stars that evolves into black holes. The black holes then rapidly segregate to the core and begin to form binaries. As the black holes are significantly more massive than the other stars, they effectively form a separate sub-system, which interacts solely with itself. The black holes form binaries and then harden through binary-single black hole interactions that occasionally eject either the binary, the single black hole, or both.

They simulated this scenario using N=2048 and N=4096 systems with 1% massive stars. The results of their simulations roughly confirm a theoretical argument based on the recoil velocity that a binary receives during an interaction. Noting that each encounter increases the binding energy by about 20% and that roughly 1/3 of this energy goes into binary recoil, the minimum binding energy E_{b min} of an ejected black hole binary is

$$ {E_{{\rm{b min}}}} \sim 36{W_0}\frac{{{M_{{\rm{bh}}}}}}{{\left\langle M \right\rangle }}kT, $$

((29))

where 〈M〉 is the average mass of a globular cluster star and W₀=〈M〉|φ₀|/kT is the dimensionless central potential. After most binaries are ejected, 〈M〉∼0.4M_⊙. After a few gigayears, nearly all of the black holes were ejected.

At the end of this phase of black hole binary ejection, there is a 50% chance that a binary remains in the cluster with no other black hole to eject it. Thus, there should be a stellar mass black hole binary remaining in about half of the galactic globular clusters. The maximum binding energy of the remaining black hole binary is E_{b min} and is also given by Equation (29). We can then approximate the distribution in energies of the remaining black hole binaries as being flat in log(E_b). The eccentricities of this population will follow a thermal distribution with P(e)=2e.

5.3.2 Monte Carlo simulations

Dynamical Monte Carlo simulations can be used to study the evolution of binary populations within evolving globular cluster models. Rasio et al. [134] have used a Monte Carlo approach (described in Joshi et al. [88, 89]) to study the formation and evolution of NS—WD binaries, which may be progenitors of the large population of millisecond pulsars being discovered in globular clusters (see Section 3.3). In addition to producing the appropriate population of binary millisecond pulsars to match observations, the simulations also indicate the existence of a population of NS-WD binaries (see Figure 8).

Figure 8

Results of the Monte Carlo simulation of NS-WD binary generation and evolution in 47 Tuc. Each small dot represents a binary system. The circles and error bars are the 10 binary pulsars in 47 Tuc with well measured orbits. Systems in A have evolved through mass transfer from the WD to the NS. Systems in B have not yet evolved through gravitational radiation to begin RLOF from the WD to the NS. Systems in C will not undergo a common envelope phase. Figure taken from Rasio et al. [134].

The tail end of the systems in group B of Figure 8 represents the NS-WD binaries that are in very short period orbits and are undergoing a slow inspiral due to gravitational radiation. These few binaries can be used to infer an order of magnitude estimate on the population of such objects in the galactic globular cluster system. If we consider that there are two binaries with orbital period less than 2000 s out of ∼10⁶M_⊙ in 47 Tuc, and assume that this rate is consistent throughout the globular cluster system as a whole, we find a total of ∼60 such binaries. Although this estimate is quite crude, it compares favorably with estimates arrived at through the encounter rate population syntheses, which are discussed in Section 5.3.3.

There is also great promise for the hybrid gas/Monte Carlo method being developed by Spurzem and Giersz [153]. Their recent simulation of the evolution of a cluster of 300,000 equal point-mass stars and 30,000 binaries yields a wealth of detail about the position and energy distribution of binaries in the cluster [58]. One expects that the inclusion of stellar evolution and a mass spectrum would produce similar detail concerning relativistic binaries.

5.3.3 Encounter rate techniques

Perhaps because of the paucity of observations of double white dwarf binaries (there is only one candidate He-CO binary [41]), there have been few population syntheses of WD-WD binaries in globular clusters. Sigurdsson and Phinney [151] use Monte Carlo simulations of binary encounters to infer populations using a static background cluster described by an isotropic King-Michie model. Their results are focused toward predicting the observable end products of binary evolution such as millisecond pulsars, cataclysmic variables, and blue stragglers. Therefore, there are no clear descriptions of relativistic binary populations provided. Davies and collaborators also use the technique of calculating encounter rates (based on calculations of cross-sections for various binary interactions and number densities of stars using King-Michie static models) to determine the production of end products of binary evolution [33, 31]. Although they also do not provide a clear description of a population of relativistic binaries, their results allow the estimation of such a population.

Using the encounter rates of Davies and collaborators [33, 31], one can follow the evolution of binaries injected into the core of a cluster. A fraction of these binaries will evolve into compact binaries which will then be brought into contact through the emission of gravitational radiation. By following the evolution of these binaries from their emergence from common envelope to contact, we can construct a population and period distribution for present day globular clusters [16]. For a globular cluster with dimensionless central potential W₀=12, Davies [31] followed the evolution of 1000 binaries over two runs. The binaries were chosen from a Salpeter IMF with exponent α=2.35, and the common envelope evolution used an efficiency parameter α_CE=0.4. One run was terminated after 15 Gyr and the population of relativistic binaries which had been brought into contact through gravitational radiation emission was noted. The second run was allowed to continue until all binaries were either in merged or contact systems. There are four classes of relativistic binaries that are brought into contact by gravitational radiation: high mass white dwarf-white dwarf binaries WD ² _a with total mass above the Chandrasekhar mass; low mass white dwarf-white dwarf binaries WD ² _b with total mass below the Chandrasekhar mass; neutron star-white dwarf binaries NW; and neutron star-neutron star binaries NS².

The number of systems brought into contact at the end of each run is given in Table 3.

Table 3 Number of relativistic binaries brought into contact through binary interactions.

In the second run, the relativistic binaries had all been brought into contact. In similar runs, this occurs after another 15 Gyr. An estimate of the present-day period distribution can be made by assuming a constant merger rate over the second 15 Gyr. Consider the total number of binaries that will merge to be described by n(t). Thus, the merger rate is η=-dn/dt. Assuming that the mergers are driven solely by gravitational radiation, we can relate n(t) to the present-day period distribution. We define n(P) to be the number of binaries with period less than P, and thus

$$ \eta = - \frac{{dn}}{{dt}} = - \frac{{dn}}{{dP}}\frac{{dP}}{{dt}}, $$

((30))

so

$$ \frac{{dn}}{{dP}} = \frac{{ - \eta }}{{dP/dt}}. $$

((31))

The merger rate is given by the number of mergers of each binary type per 1000 primordial binaries per 15 Gyr. If the orbits have been circularized (which is quite likely if the binaries have been formed through a common envelope), the evolution of the period due to gravitational radiation losses is given by [76]

$$ \frac{{dP}}{{dt}} = - {k_0}{P^{ - 5/3}}, $$

((32))

where k₀ is given by

$$ {k_0} = \frac{{96}}{5}{\left( {2\pi } \right)^{8/3}}\frac{{{G^{5/3}}}}{{{c^5}}}{{\mathcal M}^{5/3}}, $$

((33))

with the “chirp mass” M^5/3≡M₁M₂(M₁+M₂)^-1/3.

Following this reasoning and using the numbers in Table 3, we can determine the present day population of relativistic binaries per 1000 primordial binaries. To find the population for a typical cluster, we need to determine the primordial binary fraction for globular clusters. Estimates of the binary fraction in globular clusters range from 13% up to about 40% based on observations of either eclipsing binaries [5, 165, 166] or luminosity functions [138, 139]. Assuming a binary fraction of 30%, we can determine the number of relativistic binaries with short orbital period (P_orb<P_max) for a typical cluster with 10⁶M_⊙ and the galactic globular cluster system with 10^7.5M_⊙ [151] by simply integrating the period distribution from contact P_c up to P_max

$$ N = \int_{{P_{\rm{c}}}}^{{P_{\max }}} {\frac{\eta }{{{k_0}}}{P^{5/3}}dP.} $$

((34))

The value of P_c can be determined by using the Roche lobe radius of Eggleton [42],

$$ {R_{\rm{L}}} = \frac{{0.49{q^{2/3}}}}{{0.6{q^{2/3}} + \ln \left( {1 + {q^{1/3}}} \right)}}a, $$

((35))

and stellar radii as determined by Lynden-Bell and O’Dwyer [99].

The expected populations for an individual cluster and the galactic cluster system are shown in Table 4 using neutron star masses of 1.4M_⊙, white dwarf masses of 0.6M_⊙ and 0.3M_⊙, and P_max=2000 s.

Table 4 Encounter rate estimates of the population of relativistic binaries in a typical globular cluster and the galactic globular cluster system.

Although we have assumed the orbits of these binaries will be circularized, there is the possible exception of NS² binaries, which may have a thermal distribution of eccentricities if they have been formed through exchange interactions rather than through a common envelope. In this case, Equations (32) and (33) are no longer valid. An integration over both period and eccentricity, using the formulae of Pierro and Pinto [122], would be required.

5.3.4 Semi-empirical methods

The small number of observed relativistic binaries can be used to infer the population of dark progenitor systems [18]. For example, the low-mass X-ray binary systems are bright enough that we see essentially all of those that are in the galactic globular cluster system. If we assume that the ultracompact ones originate from detached WD-NS systems, then we can estimate the number of progenitor systems by looking at the time spent by the system in both phases. Let N_X be the number of ultracompact LMXBs and T_X be their typical lifetime. Also, let N_det be the number of detached WD-NS systems that will evolve to become LMXBs, and T_det be the time spent during the inspiral due to the emission of gravitational radiation until the companion white dwarf fills its Roche lobe. If the process is stationary, we must have

$$ \frac{{{N_{\rm{X}}}}}{{{T_{\rm{X}}}}} = \frac{{{N_{\det }}}}{{{T_{\det }}}}. $$

((36))

The time spent in the inspiral phase can be found from integrating Equation (32) to get

$$ {T_{\det }} = \frac{3}{{8{k_0}}}\left( {P_0^{8/3} - P_{\rm{c}}^{8/3}} \right) $$

((37))

where P₀ is the period at which the progenitor emerges from the common envelope and P_c is the period at which RLOF from the white dwarf to the neutron star begins. Thus, the number of detached progenitors can be estimated from

$$ {N_{\det }} = \frac{{{N_{\rm{X}}}}}{{{T_{\rm{X}}}}}\frac{3}{{8{k_0}}}\left( {P_0^{8/3} - P_{\rm{c}}^{8/3}} \right). $$

((38))

There are four known ultracompact LMXBs [37] with orbital periods small enough to require a degenerate white dwarf companion to the neutron star. There are six other LMXBs with unknown orbital periods. Thus, 4≤N_X≤10. The lifetime T_X is rather uncertain, depending upon the nature of the mass transfer and the timing when the mass transfer would cease. A standard treatment of mass transfer driven by gravitational radiation alone gives an upper bound of T_X∼10⁹ yr [131], but other effects such as tidal heating or irradiation may shorten this to T_X∼10⁷ yr [8, 134]. The value of P₀ depends critically upon the evolution of the neutron star-main-sequence binary, and is very uncertain. Both k₀ and P_c depend upon the masses of the WD secondary and the NS primary. For a rough estimate, we take the mass of the secondary to be a typical He WD of mass 0.4M_⊙ and the mass of the primary to be 1.4M_⊙. Rather than estimate the typical period of emergence from the common envelope, we arbitrarily choose P₀=2000 s. We can be certain that all progenitors have emerged from the common envelope by the time the orbital period is this low. The value of P_c can be determined by using Equation (35) and the radius of the white dwarf as determined by Lynden-Bell and O’Dwyer [99]. Adopting the optimistic values of N_X=10 and T_X=10⁷ yr, and evaluating Equation (37) gives T_det∼10⁷ yr. Thus, we find N_det∼1−10, which is within an order of magnitude of the numbers found through dynamical simulations (Section 5.3.2) and encounter rate estimations (Section 5.3.3).

Continuing in the spirit of small number statistics, we note that there is one known radio pulsar in a globular cluster NS-NS binary (B2127+11C) and about 50 known radio pulsars in the globular cluster system as a whole (although this number may continue to grow) [98]. We may estimate that NS-NS binaries make up roughly 1/50 of the total number of neutron stars in the globular cluster system. A lower limit on the number of neutron stars comes from estimates of the total number of active radio pulsars in clusters, giving ${N_{{\rm{N}}{{\rm{S}}^2}}} \sim {10^5}$ [97]. Thus, we can estimate the total number of NS-NS binaries to be ∼2000. Not all of these will be in compact orbits, but we can again estimate the number of systems in compact orbits by assuming that the systems gradually decay through gravitational radiation and thus

$$ \frac{{{N_{{\rm{compact}}}}}}{{{N_{{\rm{N}}{{\rm{S}}^2}}}}} = \frac{{{T_{{\rm{compact}}}}}}{{{T_{{\rm{coalesce}}}}}} $$

((39))

where N_compact is the number of systems in compact orbits (P_orb<2000 s), T_compact is the time spent as a compact system, and T_coalesce is the typical time for a globular cluster NS-NS binary to coalesce due to gravitational radiation inspiral. Adopting the coalescence time of B2127+11C as typical, T_coalesce=2×10⁸ yr [129], and integrating Equation (37) for two 1.4M_⊙ neutron stars, we find N_compact∼25. Again this value compares favorably with the values found from encounter rate estimations.

6 Prospects of Gravitational Radiation

A very exciting prospect for the observation of relativistic binaries in globular clusters lies in the fact that they will be sources of gravitational radiation. There is a phase in the evolution of most relativistic binaries during which the orbital period is slowly shrinking due to the emission of gravitational radiation. If the binary is in a circularized orbit, the gravitational radiation will be peaked strongly in the second harmonic of the orbital period, so f_gw=2f_orb. Gravitational radiation can be described by the dimensionless strain amplitude h_o. Although the strength of the gravitational radiation varies with the orientation of the binary, an angle-averaged estimate of the signal strength is [2]

$$ {h_0} = 1.5 \times {10^{ - 21}}{\left( {\frac{{{f_{{\rm{gw}}}}}}{{{{10}^{ - 3}}{\rm{Hz}}}}} \right)^{2/3}}\left( {\frac{{1{\rm{ kpc}}}}{r}} \right){\left( {\frac{{\mathcal M}}{{{M_ \odot }}}} \right)^{5/3}}. $$

((40))

At a typical globular cluster distance of r∼10 kpc and typical chirp mass of M∼0.5M_⊙, a relativistic WD-WD or WD-NS binary with P_orb=400 s will have a gravitational wave amplitude of 10^-22. This value is within the range of the proposed space-based gravitational wave observatory LISA [2].

Many globular clusters lie off the plane of the galaxy and are relatively isolated systems with known positions. The angular resolution of LISA improves with signal strength. By focusing the search for gravitational radiation using known positions of suspected sources, it is possible to increase the signal-to-noise ratio for the detected signal. Thus, the angular resolution of LISA for globular cluster sources can be on the order of the angular size of the globular cluster itself at f_gw>1 mHz. Consequently, the orbital period distribution of a globular cluster’s population of relativistic binaries can be determined through observations in gravitational radiation. We will discuss the prospects for observing each class of relativistic binaries covered in this review.

White dwarf-white dwarf binaries that are formed from a common envelope phase will be briefly visible while the recently revealed hot core of the secondary cools. These objects are most likely the “non-flickerers” of Cool et al. [26] and Edmonds et al. [41]. WD-WD binaries formed through exchange interactions may very well harbor white dwarfs which are too cool to be observed. In either case, hardening through dynamical interactions will become less likely as the orbit shrinks and the effective cross section of the binary becomes too small. These objects will then be effectively invisible in electromagnetic radiation until they are brought into contact and RLOF can begin. During this invisible phase, the orbital period is ground down through the emission of gravitational radiation until the orbital period is a few hundred seconds [16]. With a frequency of 1 to 10 mHz, gravitational radiation from such a binary will be in the band of LISA [2]. There are ∼175 such systems predicted from encounter rates (see Table 4).

White dwarf-neutron star binaries that are expected to be progenitors of the millisecond pulsars must pass through a phase of gravitational radiation after the degenerate core of the donor star emerges from the common envelope phase and before the spin-up phase begins with the onset of mass transfer from the WD to the neutron star. The orbital period at the onset of RLOF will be on the order of 1 to 2 minutes and the gravitational wave signal will be received at LISA with a signal-to-noise of 50–100 at a frequency of around 20 mHz for a globular cluster binary. Estimates of the number of such systems range from 1–10 for semi-empirical methods (Section 5.3.4) to ∼125 from encounter rates (Table 4).

Binaries with significant eccentricity will have a spectrum of harmonics of the orbital frequency, with the relative strength of the nth harmonic for eccentricity e given by [120]

$$ g\left( {n,e} \right) = \frac{{{n^4}}}{{32}}\left\{ {{{\left[ {{J_{n - 2}}\left( {ne} \right) - {J_{n - 1}}\left( {ne} \right) + \frac{2}{n}{J_n}\left( {ne} \right) + {J_{n + 1}}\left( {ne} \right) - {J_{n + 2}}\left( {ne} \right)} \right]}^2} + \left( {1 - {e^2}} \right){{\left[ {{J_{n - 2}}\left( {ne} \right) - 2{J_n}\left( {ne} \right) + {J_{n + 2}}\left( {ne} \right)} \right]}^2} + \frac{4}{{3{n^2}}}{{\left[ {{J_n}\left( {ne} \right)} \right]}^2}} \right\}, $$

((41))

where J_n is the Bessel function. The higher harmonics of sufficiently eccentric binaries (e>0.7) can be detected by LISA even though the fundamental orbital frequency is well below its sensitivity band of 1–100 mHz [15].

Although the globular cluster population of NS-NS binaries is expected to be quite small (∼10), they may have high eccentricities. The binary pulsar B2127+11Cis an example of a NS-NS binary in a globular cluster. In terms of the unknown angle of inclination i, the companion mass to the pulsar is M₂sini∼1M_⊙ and its eccentricity is e=0.68 [98]. These binaries may also be detectable by LISA. If the globular cluster systems of other galaxies follow similar evolution as the Milky Way population, these binaries may be potential sources for LIGO as gravitational radiation grinds them down to coalescence. With their high eccentricities and large chirp mass, black hole binaries will also be good potential sources for gravitational radiation from the galactic globular cluster system [17, 15].

The relatively close proximity of the galactic globular cluster system and the separations between individual globular clusters allows for the identification of gravitational radiation sources with their individual host clusters. Although the expected angular resolution of LISA is not small enough to allow for the identification of individual sources, knowledge of the positions of the clusters will allow for focused searches of the relativistic binary populations of the majority of the galactic globular clusters. Armed with a knowledge of the orbital periods of any detected binaries, concentrated searches in electromagnetic radiation can be successful in identifying relativistic binaries that may have otherwise been missed.

7 Summary

Relativistic binaries are tracers for the rich dynamical evolution of globular clusters. The populations of these objects are the result of an interplay between the gravitational dynamics of large N-body systems, the dynamics of mass transfer, the details of stellar evolution, and the effect of the gravitational field of the galaxy. The gravitational dynamics of globular clusters can enhance the population of short period binaries of main-sequence stars as well as inject compact objects such as white dwarfs and neutron stars into stellar binary systems. Once they are in such systems, the details of stellar evolution and mass transfer in close binary systems govern the likely end products of the dynamical interaction between the two stars. Furthermore, most models of the evolution of the core of a globular cluster rely on the gradual hardening and ejection of binary systems to delay the onset of core collapse. The hardening of binaries in the core of globular clusters will produce relativistic binaries, but it will also eventually eject these systems as they gain larger and larger recoil velocities in each subsequent encounter. The threshold for ejection from a globular cluster depends both upon the gravitational potential of the cluster itself and the gravitational potential of its environment generated by the Milky Way. As the globular cluster orbits the Milky Way, its local environment changes. Consequently, if other dynamical processes (such as gravothermal oscillations) do not dominate, the globular cluster’s population of relativistic binaries may also reflect the past orbital history of the globular cluster.

Over the last decade, observational techniques and technology have improved to the extent that significant discoveries are being made regularly. At this point, the bottleneck in observations of binary millisecond pulsars, low-mass X-ray binaries, and cataclysmic variables is time, not technology. As these observational techniques are brought to bear on more clusters, more discoveries are bound to be made. In the next decade, the possibility of using gravitational wave astronomy to detect relativistic binaries brings the exciting possibility of identifying the populations of electromagnetically invisible objects such as detached WD and NS binaries and black hole binaries in globular clusters. These observations can only help to improve the understanding of the complex and interesting evolution of these objects and their host globular clusters.