Numerical Hydrodynamics in Special Relativity

Abstract

This review is concerned with a discussion of numerical methods for the solution of the equations of special relativistic hydrodynamics (SRHD). Particular emphasis is put on a comprehensive review of the application of high-resolution shock-capturing methods in SRHD. Results of a set of demanding test bench simulations obtained with different numerical SRHD methods are compared. Three applications (astrophysical jets, gamma-ray bursts and heavy ion collisions) of relativistic flows are discussed. An evaluation of various SRHD methods is presented, and future developments in SRHD are analyzed involving extension to general relativistic hydrodynamics and relativistic magneto-hydrodynamics. The review further provides FORTRAN programs to compute the exact solution of a 1D relativistic Riemann problem with zero and nonzero tangential velocities, and to simulate 1D relativistic flows in Cartesian Eulerian coordinates using the exact SRHD Riemann solver and PPM reconstruction.

1 Introduction

1.1 Current fields of research

Relativity is a necessary ingredient for describing astrophysical phenomena involving compact objects. Among these phenomena are core collapse supernovae, X-ray binaries, pulsars, coalescing neutron stars, formation of black holes, micro-quasars, active galactic nuclei, superluminal jets and gamma-ray bursts. General relativistic effects must be considered when strong gravitational fields are encountered as, for example, in the case of coalescing neutron stars or near black holes. The significant gravitational wave signal produced by some of these phenomena can also only be understood in the framework of the theory of general relativity. There are, however, astrophysical phenomena which involve flows at relativistic speeds but no strong gravitational fields, and thus at least certain aspects of these phenomena can be described within the framework of special relativity.

Another field of research, where special relativistic “flows” are encountered, are heavy-ion collision experiments performed with large particle accelerators. The heavy ions are accelerated up to ultra-relativistic velocities to study various aspects of heavy ion collision physics (like, e.g., multi-particle production, the occurrence of nuclear shock waves, collective flow phenomena, or dissipative processes), to explore the equation of state for hot dense nuclear matter, and to find evidence for the existence of the quark-gluon plasma.

1.2 Overview of the numerical methods

The first attempt to solve the equations of relativistic hydrodynamics (RHD) was made by Wilson [296, 297] and collaborators [50, 123] using an Eulerian explicit finite difference code with monotonic transport. The code relies on artificial viscosity techniques [293, 243] to handle shock waves. It has been widely used to simulate flows encountered in cosmology, axisymmetric relativistic stellar collapse, accretion onto compact objects and, more recently, collisions of heavy ions. Almost all the codes for both special (SRHD) and general (GRHD) numerical relativistic hydrodynamics developed in the eighties [223, 267, 207, 206, 208, 85] were based on Wilson’s procedure. However, despite its popularity it turned out to be unable to accurately describe extremely relativistic flows (Lorentz factors larger than 2; see, e.g., [50]).

In the mid-eighties, Norman and Winkler [213] proposed a reformulation of the difference equations of SRHD with an artificial viscosity consistent with the relativistic dynamics of nonperfect fluids. The strong coupling introduced in the equations by the presence of the viscous terms in the definition of relativistic momentum and total energy densities required an implicit treatment of the difference equations. Accurate results across strong relativistic shocks with large Lorentz factors were obtained in combination with adaptive mesh techniques. However, no multi-dimensional version of this code was developed.

Attempts to integrate the RHD equations avoiding the use of artificial viscosity were performed in the early nineties. Dubal [77] developed a 2D code for relativistic magneto-hydrodynamics based on an explicit second-order Lax-Wendroff scheme incorporating a flux-corrected transport (FCT) algorithm [33]. Following a completely different approach Mann [172] proposed a multi-dimensional code for GRHD based on smoothed particle hydrodynamics (SPH) techniques [199], which he applied to relativistic spherical collapse [174]. When tested against 1D relativistic shock tubes all these codes performed similar to the code of Wilson. More recently, Dean et al. [69] have applied flux correcting algorithms for the SRHD equations in the context of heavy ion collisions. Recent developments in relativistic SPH methods [53, 261] are discussed in Section 4.2.

A major breakthrough in the simulation of ultra-relativistic flows was accomplished when high-resolution shock-capturing (HRSC) methods, specially designed to solve hyperbolic systems of conservations laws, were applied to solve the SRHD equations [179, 176, 83, 84].

1.3 Plan of the review

This review is intended to provide a comprehensive discussion of different HRSC methods and of related methods used in SRHD. However, we are not going to consider finite difference and finite volume methods based on the usage of artificial viscosity techniques which are reviewed, e.g., in the book of Wilson and Mathews [299]. Numerical methods for special relativistic MHD flows are also not included as they are beyond the scope of this review. Furthermore, we do not include numerical methods for general relativistic hydrodynamics. A comprehensive and recent discussion of such methods can be found in another article in Living Reviews in Relativity written by Font [91].

The review is organized as follows. Section 2 contains a derivation of the equations of special relativistic (perfect) fluid dynamics, as well as a discussion of their main properties. In Section 3 the most recent developments in numerical methods for SRHD are reviewed paying particular attention to high-resolution shock-capturing methods.

We have focussed on those aspects of the numerical methods more specific of SRHD, i.e., the discussion of relativistic Riemann solvers and the computation of numerical fluxes. Some comments about the extension to multi-dimensional flows are included in Section 9 (see below).

Other developments in special relativistic numerical hydrodynamics are discussed in Section 4. Numerical results obtained with different methods as well as analytical solutions for several test problems are presented in Section 6. Two astrophysical applications of SRHD are discussed in Section 7. An evaluation of the various numerical methods is given in Section 8 together with an outlook for future developments. Finally, some additional technical information including the incorporation of general equations of state is presented in Section 9.

The reader is assumed to have basic knowledge in classical [153, 62] and relativistic fluid dynamics [274, 8], as well as in finite difference/volume methods for partial differential equations [236, 214]. A discussion of modern finite volume methods for hyperbolic systems of conservation laws can be found, e.g., in [158, 161, 154]. The theory of spectral methods for fluid dynamics is developed in [42], and smoothed particle hydrodynamics is reviewed in [199].

2 Special Relativistic Hydrodynamics

2.1 Equations

Using the Einstein summation convention the equations describing the motion of a relativistic fluid are given by the five conservation laws,

$$ (\rho u^\mu )_{;\mu } = 0, $$

((1))

$$ T^{\mu \nu } ;\nu = 0, $$

((2))

where μ, v = 0, ..., 3, and where _;μ denotes the covariant derivative with respect to coordinate x^μ. Furthermore, ρ is the proper rest mass density of the fluid, u^μ its four-velocity, and T^μv is the stress-energy tensor, which for a perfect fluid can be written as

$$ T^{\mu \nu } = \rho hu^\mu u^\nu+ pg^{\mu \nu } . $$

((3))

Here, g^μv is the metric tensor, p the fluid pressure, and h the specific enthalpy of the fluid defined by

$$ h = 1 + \;\varepsilon + \frac{p} {\rho }, $$

((4))

where ε is the specific internal energy. Note that we use natural units (i.e., the speed of light c = 1) throughout this review.

In Minkowski spacetime and Cartesian coordinates (t, x¹, x², x³), the conservation equations (1, 2) can be written in vector form as

$$ \frac{{\partial {\text{u}}}} {{\partial t}} + \frac{{\partial {\text{F}}^i ({\text{u}})}} {{\partial x^i }} = 0, $$

((5))

where i = 1, 2, 3. The state vector u is defined by

$$ {\text{u}} = (D, S^1 ,S^2 ,S^3 , \tau )^T $$

((6))

and the flux vectors Fⁱ are given by

$$ {\text{F}^i} = (Dv^i ,S^1 v^i + p\delta ^{1i} + p\delta ^{2i} ,S^3 v^i + p\delta ^{3i} ,S^i - Dv^i )^{\text{T}} . $$

((7))

The five conserved quantities D, S¹, S², S³, and τ are the rest mass density, the three components of the momentum density, and the energy density (measured relative to the rest mass energy density), respectively. They are all measured in the laboratory frame, and are related to quantities in the local rest frame of the fluid (primitive variables) through

$$ D = \rho W, $$

((8))

$$ S^i = \rho hW^2 v^i ,\;\;\;\;\;i = 1,2,3, $$

((9))

$$ \tau = \rho hW^2 - p - D, $$

((10))

where vⁱ are the components of the three-velocity of the fluid

$$ v^i = \frac{{u^i }} {{u^0 }}, $$

((11))

and W is the Lorentz factor,

$$ W = u^0 = \frac{1} {{\sqrt {1 - v^i v_1 } }}. $$

((12))

The system of Equations (5) with Definitions (6, 7, 8, 9, 10, 11, 12) is closed by means of an equation of state (EOS), which we shall assume to be given in the form

$$ p = p(\rho ,\varepsilon ). $$

((13))

In the non-relativistic limit (i.e., v ≪ 1, h → 1) D, Sⁱ, and τ approach their Newtonian counterparts ρ, ρvⁱ, and ρE = ρε + ρv²/2, and Equations (5) reduce to the classical ones. In the relativistic case the equations of system (5) are strongly coupled via the Lorentz factor and the specific enthalpy, which gives rise to numerical complications (see Section 2.3).

In classical numerical hydrodynamics it is very easy to obtain vⁱ from the conserved quantities (i.e., ρ and ρvⁱ). In the relativistic case, however, the task to recover (ρ, vⁱ, p) from (D, Sⁱ, τ) is much more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the conserved quantities are advanced in time, it is necessary to compute the primitive variables from the conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial ingredient of any algorithm (see Section 9.2).

2.2 SRHD as a hyperbolic system of conservation laws

An important property of system (5) is that it is hyperbolic for causal EOS [8]. For hyperbolic systems of conservation laws, the Jacobeans ∂Fⁱ(u)/∂u have real eigenvalues and a complete set of eigenvectors (see Section 9.3). Information about the solution propagates at finite velocities given by the eigenvalues of the Jacobeans. Hence, if the solution is known (in some spatial domain) at some given time, this fact can be used to advance the solution to some later time (initial value problem). However, in general, it is not possible to derive the exact solution for this problem. Instead one has to rely on numerical methods which provide an approximation to the solution. Moreover, these numerical methods must be able to handle discontinuous solutions, which are inherent to nonlinear hyperbolic systems.

The simplest initial value problem with discontinuous data is called a Riemann problem, where the one-dimensional initial state consists of two constant states separated by a discontinuity. The majority of modern numerical methods, the so-called Godunov-type methods, are based on exact or approximate solutions of Riemann problems. Because of its theoretical and numerical importance, we discuss the solution of the special relativistic Riemann problem in the next Section 2.3.

2.3 Exact solution of the Riemann problem in SRHD

Let us first consider the one-dimensional special relativistic flow of a perfect fluid in the absence of a gravitational field. The Riemann problem then consists of computing the breakup of a discontinuity, which initially separates two arbitrary constant states L (left) and R (right) in the fluid (see Figure 1 with L ≡ 1 and R ≡ 5). For classical hydrodynamics the solution can be found, e.g., in [62]. In the case of SRHD, the Riemann problem was considered by Martí and Müller [180], who derived an exact solution for the case of pure normal flow generalizing previous results for zero initial velocities [276]. More recently, Pons, Martí and Müller [234] have obtained the general solution in the case of non-zero tangential speeds.

The solution to this problem is self-similar, because it only depends on the two constant states defining the discontinuity v_L and v_R, where v - (p, ρ, v^x, v^y, v^z), and on the ratio (x - x₀)/(t - t₀), where x₀ and t₀ are the initial location of the discontinuity and the time of breakup, respectively. Both in relativistic and classical hydrodynamics the discontinuity decays into two elementary nonlinear waves (shocks or rarefactions) which move in opposite directions towards the initial left and right states. Between these waves two new constant states V_L* and v_R* (note that V_L* ≡ 3 and v_R* ≡ 4 in Figure 1) appear, which are separated from each other by a contact discontinuity moving with the fluid. Accordingly, the time evolution of a Riemann problem can be represented as

$$ {\text{I}} \to {\text{L}} \mathcal{W}_ \leftarrow {\text{L}}_* \;\mathcal{C}\;{\text{R}}_* \;\mathcal{W}_ \to {\text{R}}, $$

((14))

where $\mathcal{W}$ and $\mathcal{C}$ denote a simple wave (shock or rarefaction) and a contact discontinuity, respectively. The arrows (← / →) indicate the direction (left / right) from which fluid elements enter the corresponding wave.

As in the Newtonian case, the compressive character of shock waves (density and pressure rise across the shock) allows us to discriminate between shocks ($\mathcal{S}$) and rarefaction waves ($\mathcal{R}$):

$$ \mathcal{W}_{ \leftarrow ( \to )} = \left\{ {\begin{array}{*{20}c} {\mathcal{R}_{ \leftarrow ( \to )} } \\ {\mathcal{S}_{ \leftarrow ( \to )} } \\ \end{array} \;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}c} {\text{for}} \\ {\text{for}} \\ \end{array} \;\begin{array}{*{20}c} {p_b \leqslant p_a ,} \\ {p_b > p_a ,} \\ \end{array} } \right. $$

((15))

where p is the pressure, and subscripts a and b denote quantities ahead and behind the wave. For the Riemann problem a ≡ L(R) and b ≡ L_*(R_*) for ${\mathcal{W}_ \leftarrow }$ and ${\mathcal{W}_ \to }$, respectively. Thus, the possible types of decay of an initial discontinuity can be reduced to

$$\begin{array}{*{20}c} { \bullet \;\;I\; \to \;L\;\mathcal{S}_ \leftarrow L_* \;\mathcal{C}\;R_* \;\mathcal{S}_ \to R,\;\;\;\;\;\;\;p_L < p_{L_* } = p_{R_* } \geqslant p_R ,} \\ { \bullet \;\;I\; \to \;L\;\mathcal{S}_ \leftarrow L_* \;\mathcal{C}\;R_* \;\mathcal{R}_ \to R,\;\;\;\;\;\;\;p_L < p_{L_* } = p_{R_* } \leqslant p_R ,} \\ { \bullet \;\;I\; \to \;L\;\mathcal{R}_ \leftarrow L_* \;\mathcal{C}\;R_* \;\mathcal{R}_ \to R,\;\;\;\;\;\;\;p_L \geqslant p_{L_* } = p_{R_* } \leqslant p_R .} \\ \end{array}$$

((16))

Across the contact discontinuity the density exhibits a jump, whereas pressure and normal velocity are continuous (see Figure 1). As in the classical case, the self-similar character of the flow through rarefaction waves and the Rankine-Hugoniot conditions across shocks provide the relations to link the intermediate states v_S* (S = L, R) with the corresponding initial states v_S. They also allow one to express the normal fluid flow velocity in the intermediate states (v ^x_S* for the case of an initial discontinuity normal to the x axis) as a function of the pressure p_S* in these states.

The solution of the Riemann problem consists in finding the intermediate states L_* and R_*, as well as the positions of the waves separating the four states (which only depend on L, L_*, R_*, and R). The functions ${\mathcal{W}_ \to }$ and ${\mathcal{W}_ \leftarrow }$ allow one to determine the functions v ^x_R* (p) and v ^x_L* (p), respectively. The pressure p_* and the flow velocity v ^x_* in the intermediate states are then given by the condition

$$ v_{R_* }^x (p_* ) = v_{L_* }^x (p_* ) = v_*^x , $$

((17))

where p_* - P_L* - P_R*.

In the case of relativistic hydrodynamics, the major difference to classical hydrodynamics stems from the role of tangential velocities. While in the classical case the decay of the initial discontinuity does not depend on the tangential velocity (which is constant across shock waves and rarefactions), in relativistic calculations the components of the flow velocity are coupled by the presence of the Lorentz factor in the equations. In addition, the specific enthalpy also couples with the tangential velocities, which becomes important in the thermodynamically ultrarelativistic regime.

The functions v ^x_s* (p) are defined by

$$v_{S_* }^x (p) = \left\{ {\begin{array}{*{20}c} {\mathcal{R}^\text{S} (p),} \\ {\mathcal{S}^\text{S} (p),} \\ \end{array} } \right.\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}c} {\text{if}\;p \leqslant p_\text{S} ,} \\ {\text{if}\;p > p_\text{S} ,} \\ \end{array} $$

((18))

where ${\mathcal{R}^S}(p)\;\left( {{\mathcal{S}^S}(p)} \right)$ denotes the family of all states which can be connected by a rarefaction (shock) with a given state vs ahead of the wave.

The fact that one Riemann invariant is constant across any rarefaction wave provides the relation needed to derive the function ${\mathcal{R}^\text{S}}$. In differential form, the function reads

$$ \frac{{dv^x }} {{dp}} = \pm \frac{1} {{phW^2 c_\text{s} }}\frac{1} {{\sqrt {1 + g(\xi _ \pm ,v^x ,v^t )} }}, $$

((19))

Figure 1

Schematic solution of a Riemann problem in special relativistic hydrodynamics. The initial state at t = 0 (top figure consists of two constant states 1 and 5 with p₁ > p₅, ρ₁ > ρ₅, and v₁ = v₂ = 0 separated by a diaphragm at x_D. The evolution of the flow pattern once the diaphragm is removed (middle figure is illustrated in a spacetime diagram (bottom figure with a shock wave (solid line and a contact discontinuity (dashed line moving to the right. The bundle of solid lines represents a rarefaction wave propagating to the left.

where ${v^t} = \sqrt {{{({v^y})}^2} + {{({v^z})}^2}}$ is the absolute value of the tangential velocity, and

$$ g(\xi _ \pm ,v^x ,v^t ) = \frac{{(v^t )^2 (\xi _ \pm ^2 - 1)}} {{(1 - \xi _ \pm v^x )^2 }}, $$

((20))

and where

$$ \xi _ \pm= \frac{{v^x (1 - c_\text{S}^2 ) \pm c_\text{S} \sqrt {(1 - v^2 )[1 - v^2 c_\text{S}^2 - (v^x )^2 (1 - c_\text{S}^2 )]} }} {{1 - v^2 c_\text{S}^2 }}, $$

((21))

the + (-) sign corresponding to S = R (S = L). In the previous expressions, c_s stands for the local sound speed.

Considering that in a Riemann problem the state ahead of the rarefaction wave is known, the integration of Equation (19) allows one to connect the states ahead (S) and behind the rarefaction wave. Moreover, using Equation (21), the EOS, and the following relation obtained from the constraint hWv^t = constant., that holds across the rarefaction wave,

$$ v^t = h_{\text{s}} W_{\text{s}} v_{\text{s}}^t \left( {\frac{{1 - (v^x )^2 }} {{h^2 + (h_{\text{s}} W_{\text{s}} v_{\text{s}}^t )^2 }}} \right)^{1/2} , $$

((22))

the ODE can be integrated, the solution being only a function of p. Let us point out that the integration of Equation (19) is along an adiabat of the EOS.

In the limit of zero tangential velocities, v^t = 0, the function g does not contribute. In this limit and in the case of an ideal gas EOS one has

$${W^2}d{v^x} = \pm \frac{{{c_s}}}{{\gamma p}}dp = \pm \frac{{{c_s}}}{\rho }d\rho ,$$

((23))

(where γ is the adiabatic exponent of the EOS) recovering expression (30) in [180]. The equation can be then integrated to give [180]

$${\mathcal{R}^\text{S}}(p) = \frac{{(1 + {v_\text{S}}){A_ \pm }(p) - (1 - {v_\text{S}})}}{{(1 + {v_\text{S}}){A_ \pm }(p) - (1 - {v_\text{S}})}},$$

((24))

with

$${A_ \pm }(p) = {\left( {\frac{{\sqrt {\gamma - 1} - c(p)\sqrt {\gamma - 1} + {c_\text{s}}\text{s}}}{{\sqrt {\gamma - 1} - c(p)\sqrt {\gamma - 1} + {c_\text{s}}\text{s}}}} \right)^{ \pm \frac{2}{{\sqrt {\gamma - 1} }}}},$$

((25))

the + (-) sign of A_± corresponding to S = L (S = R). In the above equation, c_{s S} is the sound speed of the state v_{s S}, and c(p) is given by

$$c(p) = {\left( {\frac{{\gamma (\gamma - 1)p}}{{(\gamma - 1){\rho _\text{S}}{{(p/{p_\text{S}})}^{1/\gamma }} + \gamma p}}} \right)^{1/2}}.$$

((26))

The family of all states ${\mathcal{S}^\text{S}}(p)$, which can be connected through a shock with a given state v_S ahead of the wave, is determined by the shock jump conditions. One obtains

$${\mathcal{S}^\text{S}}(p) = \left( {{h_\text{S}}{W_\text{S}}v_\text{S}^x \pm \frac{{p - {p_\text{S}}}}{{j(p)\sqrt {1 - {V_ \pm }{{(p)}^2}} }}} \right){\left[ {{h_\text{S}}{W_\text{S}} + (p - {p_\text{S}})\left( {\frac{1}{{{\rho _\text{S}}{W_\text{S}}}} \pm \frac{{v_\text{S}^x}}{{j(p)\sqrt {1 - {V_ \pm }{{(p)}^2}} }}} \right)} \right]^{ - 1}},$$

((27))

where the + (-) sign corresponds to S = R (S = L). V₊ (p) and V_-(p) denote the shock velocities for shocks propagating to the right and left, respectively. They are given by

$${V_ \pm }(p) = \frac{{\rho _\text{S}^2W_\text{S}^2v_\text{S}^x \pm {{(p)}^2}\sqrt {1 + \rho _\text{S}^2W_\text{S}^2(1 - {{(v_\text{S}^x)}^2})/j{{(p)}^2}} }}{{\rho _\text{S}^2W_\text{S}^2 + j{{(p)}^2}}}$$

((28))

Tangential velocities in the initial states are hidden within the flow Lorentz factor W_S. On the other hand, j(p) stands for the modulus of the mass flux across the shock front,

$$j(p) = \sqrt {\frac{{{p_\text{S}} - p}}{{\frac{{h_\text{S}^2 - h{{(p)}^2}}}{{{p_\text{S}} - p}} - \frac{{2{h_\text{S}}}}{{{\rho _\text{S}}}}}}} ,$$

((29))

where the enthalpy h(p) of the state behind the shock can be obtained from the Taub adiabat,

$${h^2} - h_\text{S}^2 = \left( {\frac{h}{\rho } + \frac{{{h_\text{S}}}}{{{\rho _\text{S}}}}} \right)(p - {p_\text{S}}).$$

((30))

in the general case, the above nonlinear equation must be solved together with the EOS to obtain the post-shock enthalpy as a function of p. In the case of ideal gas EOS with constant adiabatic index, the post-shock density ρ can be easily eliminated, and the post-shock enthalpy is the (unique) positive root of the quadratic equation [180]

$$\left( {1 + \frac{{(\gamma - 1)({p_\text{S}} - p)}}{{\gamma p}}} \right){h^2} - \frac{{(\gamma - 1)({p_\text{S}} - p)}}{{\gamma p}}h + \frac{{{h_\text{S}}({p_\text{S}} - p)}}{{{\rho _\text{S}}}} - h_\text{S}^2 = 0.$$

((31))

Finally, the tangential velocities in the post-shock states can be obtained from [234]

$${v^t} = {h_\text{S}}{W_\text{S}}v_\text{S}^t{\left( {\frac{{1 - {{({v^x})}^2}}}{{{h^2} + {{({h_\text{S}}{W_\text{S}}v_\text{S}^t)}^2}}}} \right)^{1/2}}.$$

((32))

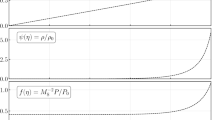
Figure 2 shows the solution of a particular mildly relativistic Riemann problem for different values of the tangential velocity. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The range of possible solutions in the (p, v^x)-plane is marked by the shaded region. While the pressure in the intermediate state can take any value between P_L and P_R, the normal flow velocity can be arbitrarily close to zero in the case of an extremely relativistic tangential flow. The values of the tangential velocity in the states L_* and R_* are obtained from the value of the corresponding functions at v^x in the lower panel of Figure 2. The influence of initial left and right tangential velocities on the solution of a Riemann problem is enhanced in highly relativistic problems. We have computed the solution of one such problem (see Section 6.2.2 below, Problem 2) for different combinations of v ^t_L and v ^t_R . The initial data are p_L = 10³, ρ_L = 1, v ^x_L = 0; p_R = 10⁻², ρ_R = 1, v ^x_R = 0, and the 9 possible combinations of v ^t_L,R = 0, 0.9, 0.99. The results are given in Figure 3 and Table 1, and a complete discussion can be found in [234].

Finally, let us note that the procedure to obtain the pressure in the intermediate states p_* is valid for general EOS. Once p_* has been obtained, the remaining state quantities and the complete Riemann solution,

$$\text{u} = \text{u}\left( {\frac{{x - {x_0}}}{{t - {t_0}}};{\text{u}_\text{L}},{\text{u}_\text{R}}} \right),$$

((33))

can be easily derived. In Section 9.4, we provide two FORTRAN programs called RIEMANN (Section 9.4.1) and RIEMANN-VT (Section 9.4.2), which allow one to compute the exact solution of an arbitrary special relativistic Riemann problem for an ideal gas EOS with constant adiabatic index, both with zero and non-zero tangential speeds using the algorithm discussed above.

Solving a Riemann problem involves the solution of an algebraic equation for the pressure (Equation (17)). Moreover, the functional form of this equation depends on the wave pattern under consideration (see expressions (16). In a recent paper [240], Rezzolla and Zanotti have presented a procedure, suitable for implementation into an exact Riemann solver in one dimension, which

Figure 2

Graphical solution in the (p, v^x)-plane (upper panel) and in the (v^t, v^x)-plane (lower panel of the relativistic Riemann problem with initial data p_L = 1.0, ρ_L = 1.0, v ^x_L = 0.0, and p_R = 0.1, ρ_R = 0.125, v ^x_R = 0.0 for different values of the tangential velocity v^t = 0, 0.5, 0.9, 0.999, represented by solid, dashed, dashed-dotted and dotted lines, respectively. An ideal gas EOS with γ = 1.4 was assumed. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The value of the tangential velocity in the states L_* and R_* is obtained from the value of the corresponding functions at v^x in the lower panel, and I₀ gives the solution for vanishing tangential velocity. The range of possible solutions is given by the shaded region in the upper panel.

Figure 3

Analytical pressure, density and flow velocity profiles at t = 0.4 for the relativistic Riemann problem with initial data p_L = 10³, ρ_L = 1.0, v ^x_L = 0.0, and p_R = 10⁻², ρ_R = 1.0, v ^x_R = 0.0, varying the values of the tangential velocities. From left to right, v ^t_R = 0, 0.9, 0.99 and from top to bottom v ^t_L = 0, 0.9, 0.99. An ideal EOS with γ = 5/3 was assumed.

Table 1 Solution of the relativistic Riemann problem at t = 0.4 with initial data p_L = 10³, ρ_L = 1.0, v ^x_L = 0.0, p_R = 10⁻², ρ_R = 1.0, and v ^x_R = 0.0 for 9 different combinations of tangential velocities in the left (v ^t_L ) and right (v ^t_R ) initial state. An ideal EOS with γ = 5/3 was assumed. The various quantities in the table are: the density in the intermediate state left (ρ_L*) and right (ρ_R*) of the contact discontinuity, the pressure in the intermediate state (p_*), the flow speed in the intermediate state (v ^x_* ), the speed of the shock wave (V_s), and the velocities of the head (ξ_h) and tail (ξ_t) of the rarefaction wave.

removes the ambiguity arising from the wave pattern. That method exploits the fact that the expression for the relative velocity between the two initial states is a (monotonic) function of the unknown pressure, p_*, which determines the wave pattern. Hence, comparing the value of the (special relativistic) relative velocity between the initial left and right states with the values of the limiting relative velocities for the occurrence of the wave patterns (16), one can determine a priori which of the three wave patterns will actually result (see Figure 4). In [241] the authors extend the above procedure to multi-dimensional flows.

Figure 4

Relative velocity between the two initial states 1 and 2 as a function of the pressure at the contact discontinuity. Note that the curve shown is given by the continuous joining of three different curves describing the relative velocity corresponding to two shocks (dashed line, one shock and one rarefaction wave (dotted line, and two rarefaction waves (continuous line, respectively. The joining of the curves is indicated by filled circles. The small inset on the right shows a magnification for a smaller range of p_* and the filled squares indicate the limiting values for the relative velocities ${({\tilde v_{12}})_{2\text{S}}},{({\tilde v_{12}})_{\text{SR}}},{({\tilde v_{12}})_{2\text{R}}}$ (from [240]).

3 High-Resolution Shock-Capturing Methods

The application of high-resolution shock-capturing (HRSC) methods caused a revolution in numerical SRHD. These methods satisfy in a quite natural way the basic properties required for any acceptable numerical method:

• high order of accuracy,

• stable and sharp description of discontinuities, and

• convergence to the physically correct solution.

Moreover, HRSC methods are conservative, and because of their shock capturing property discontinuous solutions are treated both consistently and automatically whenever and wherever they appear in the flow.

As HRSC methods are written in conservation form, the time evolution of zone averaged state vectors is governed by some functions (the numerical fluxes) evaluated at zone interfaces. Numerical fluxes are mostly obtained by means of an exact or approximate Riemann solver, although symmetric schemes can also be implemented. High resolution is usually achieved by using monotonic polynomials in order to interpolate the approximate solutions within numerical cells.

Solving Riemann problems exactly involves time-consuming computations, which are particularly costly in the case of multi-dimensional SRHD due to the coupling of the equations through the Lorentz factor (see Section 2.3). Therefore, as an alternative, the usage of approximate Riemann solvers has been proposed.

In remainder of this section we summarize the computation of the numerical fluxes in a number of methods for numerical SRHD. Methods based on exact Riemann solvers are discussed in Sections 3.1 and 3.2, while those based on approximate solvers are discussed in Sections 3.3, 3.4, 3.5, 3.6, 3.7, and 3.8. Symmetric schemes are also presented in Section 3.9. Readers not familiar with HRSC methods are referred to Section 9.5, where the basic properties of these methods as well as an outline of the recent developments are described. Let us note that the focus of our review are one-dimensional versions of the numerical methods and algorithms. Multi-dimensional flow problems can be handled by standard means which are briefly reviewed in Section 9.5.

3.1 Relativistic PPM

Martí and Müller [181] have used the procedure discussed in Section 2.3 to construct an exact Riemann solver, which they then incorporated in an extension of the PPM method [60] for 1D SRHD. In their relativistic PPM method, numerical fluxes are calculated according to

$${\hat {\text{F}}^{ \text{RPPM}}} = { \text{F}( \text{u}(0;{\text{u}_ \text{L}},{\text{u}_ \text{R}}))},$$

((34))

where u_L and u_R are approximations of the state vector at the left and right side of a zone interface obtained by a second-order accurate interpolation in space and time, and u(0; u_L, u_R) is the solution of the Riemann problem defined by the two interpolated states at the position of the initial discontinuity.

The PPM interpolation algorithm described in [60] gives monotonic conservative parabolic profiles of variables within a numerical zone. In the relativistic version of PPM, the original interpolation algorithm is applied to zone averaged values of the primitive variables v = (p, ρ, v), which are obtained from zone averaged values of the conserved quantities u. For each zone j, the quartic polynomial with zone averaged values a_j-2, a_j-1, a_j, a_j+1, and a_j+2 (where a = ρ, p, v) is used to interpolate the structure inside the zone. In particular, the values of a at the left and right interface of the zone, a_L,j and a_R,j, are obtained this way. These reconstructed values are then modified such that the parabolic profile, which is uniquely determined by a_L,j, a_R,j and a_j, is monotonic inside the zone.

The time-averaged fluxes at an interface j + 1/2 separating zones j and j + 1 are computed from two spatially averaged states ${v_{j + \tfrac{1}{2},\text{L}}}$ and ${v_{j + \tfrac{1}{2},\text{R}}}$ at the left and right side of the interface, respectively. These left and right states are constructed taking into account the characteristic information reaching the interface from both sides during the time step. In the relativistic version of PPM the same procedure as in [60] has been followed, using the characteristic speeds and Riemann invariants of the equations of relativistic hydrodynamics. The results presented in [181] were obtained with an Eulerian code (rPPM) based on this method. The corresponding FORTRAN program rPPM is provided in Section 9.4.3. A relativistic Lagrangian version of the original PPM method in spherical coordinates and spherical symmetry has been developed by Daigne and Mochkovich [66].

3.2 Relativistic Glimm’s method

Wen et al. [295] have extended Glimm’s random choice method [104] to 1D SRHD. They developed a first-order accurate hydrodynamic code combining Glimm’s method (using an exact Riemann solver) with standard finite difference schemes.

In the random choice method, given two adjacent states u ⁿ _j and u ⁿ _j+1 at time tⁿ, the value of the numerical solution at time t^n+1/2 and position x_j+1/2 is given by the exact solution u(x, t) of the Riemann problem evaluated at a randomly chosen point inside zone (j, j + 1), i.e.,

$$\text{u}_{j + \tfrac{1}{2}}^{n + \tfrac{1}{2}} = \text{u}\left( {\frac{{(j + {\xi _n})\Delta x}}{{n + \tfrac{1}{2}\Delta t}};\text{u}_j^n,{\text{u}}_{j + 1}^n} \right),$$

((35))

where ξ is a random number in the interval [0,1].

Besides being conservative on average, the main advantages of Glimm’s method are that it produces both completely sharp shocks and contact discontinuities, and that it is free of diffusion and dispersion errors.

Chorin [52] applied Glimm’s method to the numerical solution of homogeneous hyperbolic conservation laws. Colella [57] proposed an accurate procedure of randomly sampling the solution of local Riemann problems, and investigated the extension of Glimm’s method to two dimensions using operator splitting methods.

3.3 Two-shock approximation for relativistic hydrodynamics

This approximate Riemann solver is obtained from a relativistic extension of Colella’s method [57] for classical fluid dynamics, where it has been shown to handle shocks of arbitrary strength [57, 300]. In order to construct Riemann solutions in the two-shock approximation one analytically continues shock waves towards the rarefaction side (if present) of the zone interface instead of using an actual rarefaction wave solution. Thereby one gets rid of the coupling of the normal and tangential components of the flow velocity (see Section 2.3), and the remaining minor algebraic complications are the Rankine-Hugoniot conditions across oblique shocks. Balsara [13] has developed an approximate relativistic Riemann solver of this kind by solving the jump conditions in the shocks’ rest frames in the absence of transverse velocities, after appropriate Lorentz transformations. Dai and Woodward [64] have developed a similar Riemann solver based on the jump conditions across oblique shocks making the solver more efficient.

Table 2 gives the converged solution for the intermediate states obtained with both Balsara’s and Dai and Woodward’s procedure for the case of the Riemann problems defined in Section 6.2 (involving strong rarefaction waves) together with the exact solution. Despite the fact that both approximate methods involve very different algebraic expressions, their results differ by less than 2%. However, the discrepancies are much larger when compared with the exact solution (up to a 100% error in the density of the left intermediate state in Problem 2). The accuracy of the two-shock approximation should be tested in the ultra-relativistic limit, where the approximation can produce large errors in the Lorentz factor (in the case of Riemann problems involving strong rarefaction waves) with important implications for the fluid dynamics. Finally, the suitability of the two-shock approximation for Riemann problems involving transversal velocities still needs to be tested.

Table 2 Pressure p_*, velocity v_*, and densities ρ_L* (left), ρ_R* (right) for the intermediate state obtained for the two-shock approximation of Balsara (B) [13] and of Dai and Woodward (DW) [64] compared to the exact solution (Exact) for the Riemann problems defined in Section 6.2.

3.4 Roe-type relativistic solvers

Linearized Riemann solvers are based on the exact solution of Riemann problems of a modified system of conservation equations obtained by a suitable linearization of the original system. This idea was put forward by Roe [247], who developed a linearized Riemann solver for the equations of ideal (classical) gas dynamics. Eulderink et al. [83, 84] have extended Roe’s Riemann solver to the general relativistic system of equations in arbitrary spacetimes. Eulderink uses a local linearization of the Jacobian matrices of the system fulfilling the properties demanded by Roe in his original paper.

Let $\mathcal{B} = \partial \text{F}/\partial \text{u}$ be the Jacobian matrix associated with one of the fluxes F of the original system, and u the vector of unknowns. Then, the locally constant matrix $\tilde {\mathcal{B}}$, depending on u_L and u_R (the left and right state defining the local Riemann problem), must have the following four properties:

• 1. It constitutes a linear mapping from the vector space u to the vector space F.

• 2. As ${u_L} \to {u_R} \to u,\;\tilde {\mathcal{B}}({u_L},{u_R}) \to \mathcal{B}(u)$.

• 3. For any $\tilde {\mathcal{B}}({u_L},{u_R})({u_R} - {u_L}) = F({u_R}) - F({u_L})$.

• 4. The eigenvectors of $\tilde {\mathcal{B}}$ are linearly independent.

Conditions 1 and 2 are necessary if one is to recover smoothly the linearized algorithm from the nonlinear version. Condition 3 (supposing Condition 4 is fulfilled) ensures that if a single discontinuity is located at the interface, then the solution of the linearized problem is the exact solution of the nonlinear Riemann problem.

Once a matrix $\tilde {\mathcal{B}}$ satisfying Roe’s conditions has been obtained for every numerical interface, the numerical fluxes are computed by solving the locally linear system. Roe’s numerical flux is then given by

$${\hat F^{Roe}} = \frac{1}{2}\left( {F({u_L}) + F({u_R}) - {{\sum\limits_p {\left| {{{\tilde \lambda }^{(p)}}} \right|\tilde \alpha } }^{(p)}}{{\tilde r}^{(p)}}} \right),$$

((36))

with

$${\tilde \alpha ^{(p)}} = {\tilde {\text{l}}^{(p)}} \cdot ({\text{u}_\text{R}} - {\text{u}_\text{L}}),$$

((37))

where ${\tilde \lambda ^{(p)}},\;{\tilde r^{(p)}},\;\text{and}\;{\tilde I^{(p)}}$ are the eigenvalues and the right and left eigenvectors of $\tilde {\mathcal{B}}$, respectively (p runs from 1 to the number of equations of the system).

Roe’s linearization for the relativistic system of equations in a general spacetime can be expressed in terms of the average state [83, 84]

$$\tilde {\text{w}} = \frac{{{\text{w}_\text{L}} + {\text{w}_\text{R}}}}{{{k_\text{L}} + {k_\text{R}}}},$$

((38))

with

$$w = \left( {k{u^{0,}}k{u^{1,}}k{u^{2,}}k{u^3},k\frac{p}{{\rho h}}} \right)$$

((39))

and

$${k^2} = \sqrt { - g} \rho h,$$

((40))

where g is the determinant of the metric tensor g_μv. The role played by the density ρ in case of the Cartesian non-relativistic Roe solver as a weight for averaging, is taken over in the relativistic variant by k, which apart from geometrical factors tends to ρ in the non-relativistic limit. A Riemann solver for special relativistic flows and the generalization of Roe’s solver to the Enter equations in arbitrary coordinate systems are easily deduced from Eulderink’s work. The results obtained in 1D test problems for ultra-relativistic flows (up to Lorentz factors of 625) in the presence of strong discontinuities and large gravitational background fields demonstrate the excellent performance of the Eulderink-Roe solver [84].

Relaxing Condition 3 above, Roe’s solver is no longer exact for shocks but still produces accurate solutions. Moreover, the remaining conditions are fulfilled by a large number of averages. The 1D general relativistic hydrodynamic code developed by Romero et al. [249] uses flux formula (36) with an arithmetic average of the primitive variables at both sides of the interface. It has successfully passed a long series of tests including the spherical version of the relativistic shock reflection (see Section 6.1).

Roe’s original idea has been exploited in the so-called local characteristic approach (see, e.g., [307]). This approach relies on a local linearization of the system of equations by defining at each point a set of characteristic variables, which obey a system of uncoupled scalar equations. This approach has proven to be very successful, because it allows for the extension to systems of scalar nonlinear methods. Based on the local characteristic approach are the methods developed by Marquina et al. [176] and Dolezal and Wong [74], which both use high-order reconstructions of the numerical characteristic fluxes, namely PHM [176] and ENO [74] (see Section 9.5).

3.5 Falle and Komissarov upwind scheme

Instead of starting from the conservative form of the hydrodynamic equations, one can use a primitive variable formulation in quasi-linear form,

$$\frac{{\partial v}}{{\partial t}} + \mathcal{A}\frac{{\partial v}}{{\partial x}} = 0,$$

((41))

where v is any set of primitive variables. A local linearization of the above system allows one to obtain the solution of the Riemann problem, and from this the numerical fluxes needed to advance a conserved version of the equations in time.

Falle and Komissarov [89] have considered two different algorithms to solve the local Riemann problems in SRHD by extending the methods devised in [87]. In a first algorithm, the intermediate states of the Riemann problem at both sides of the contact discontinuity, v_L* and v_R*, are obtained by solving the system

$${\text{v}_{{\text{L}_*}}} = {\text{v}_\text{L}} + {b_\text{L}}\text{r}_\text{L}^ - ,\;\;\;\;\;\;\;\;\;{\text{v}_{{\text{R}_*}}} = {\text{v}_\text{R}} + {b_\text{R}}\text{r}_\text{R}^ + ,$$

((42))

where r ⁻_L is the right eigenvector of $\mathcal{A}({v_L})$ associated with sound waves moving upstream, and r ⁺_R is the right eigenvector of $\mathcal{A}({v_R})$ of sound waves moving downstream. The continuity of pressure and of the normal component of the velocity across the contact discontinuity allows one to obtain the wave strengths b_L and b_R from the above expressions, and hence the linear approximation to the intermediate state v_*(v_L, v_R).

In the second algorithm proposed by Falle and Komissarov [89], a linearization of system (41) is obtained by constructing a constant matrix $\tilde {\mathcal{A}}({v_L},{v_R}) = \mathcal{A}\left( {\tfrac{1}{2}({v_L} + {v_R})} \right)$. The solution of the corresponding Riemann problem is that of a linear system with matrix $\tilde {\mathcal{A}}$, i.e.,

$${\text{v}_*} = {\text{v}_\text{L}} + \sum\limits_{{{\tilde \lambda }^{(p)}} < 0} {{{\tilde \alpha }^{(p)}}{{\tilde r}^{(p)}},} $$

((43))

or, equivalently,

$${\text{v}_*} = {\text{v}_\text{R}} + \sum\limits_{{{\tilde \lambda }^{(p)}} > 0} {{{\tilde \alpha }^{(p)}}{{\tilde r}^{(p)}},} $$

((44))

with

$${\tilde \alpha ^{(p)}} = {\tilde {\text{l}}^{(p)}} \cdot ({\text{v}_\text{R}} - {\text{v}_\text{L}}),$$

((45))

where ${\tilde \lambda ^{(p)}},{\tilde r^{(p)}}$, and ${\tilde I^{(p)}}$ are the eigenvalues and the right and left eigenvectors of $\tilde {\mathcal{A}}$, respectively (p runs from 1 to the number of equations of the system).

In both algorithms, the final step involves the computation of the numerical fluxes for the conservation equations,

$${\hat {\text{F}}^{\text{FK}}} = \text{F}(\text{u}({\text{v}_*}({\text{v}_\text{L}},{\text{v}_\text{R}}))).$$

((46))

3.6 Relativistic HLL method (RHLLE)

Schneider et al. [256] have proposed to use the method of Harten, Lax and van Leer (HLL hereafter [122]) to integrate the equations of SRHD. This method avoids the explicit calculation of the eigenvalues and eigenvectors of the Jacobian matrices and is based on an approximate solution of the original Riemann problems with a single intermediate state

$${\text{u}^{\text{HLL}}}\left( {\frac{x}{t};{\text{u}_\text{L}},{\text{u}_\text{R}}} \right) = \left\{ {\begin{array}{*{20}{c}} {{\text{u}_\text{L}}} \\ {{\text{u}_*}} \\ {{\text{u}_\text{R}}} \end{array}\;\;\;\;\;\;\begin{array}{*{20}{c}} {\text{for}} \\ {\text{for}} \\ {\text{for}} \end{array}\;\begin{array}{*{20}{c}} {x{ < _L}t,\;\;\;\;\;\;\;\;\;\;} \\ {{a_\text{L}}t \leqslant x \leqslant {a_\text{R}}t,} \\ {x > {a_\text{R}}t,\;\;\;\;\;\;\;\;\;} \end{array}} \right.$$

((47))

where a_L and a_R are lower and upper bounds for the smallest and largest signal velocities, respectively. The intermediate state u_* is determined by requiring consistency of the approximate Riemann solution with the integral form of the conservation laws in a grid zone. The resulting integral average of the Riemann solution between the slowest and fastest signals at some time is given by

$${\text{u}_*} = \frac{{{a_\text{R}}{\text{u}_\text{R}} - {a_\text{L}}{\text{u}_\text{L}} - \text{F}({\text{u}_\text{R}}) + \text{F}({\text{u}_\text{L}})}}{{{a_\text{R}} - {a_\text{L}}}},$$

((48))

and the numerical flux by

$${\hat {\text{F}}^{\text{HLL}}} = \frac{{a_\text{R}^ +\text{ F}({\text{u}_\text{L}}) - a_\text{L}^ - \text{F}({\text{u}_\text{R}}) + a_\text{R}^ + a_\text{L}^ - ({\text{u}_\text{R}} - {\text{u}_\text{L}})}}{{a_\text{R}^ + - a_\text{L}^ - }},$$

((49))

where

$$a_\text{L}^ - = \min \left\{ {0,{a_\text{L}}} \right\},\;\;\;\;\;\;\;\;\;\;\;\;a_\text{R}^ + = \max \left\{ {0,{a_\text{R}}} \right\}.$$

((50))

An essential ingredient of the HLL scheme are good estimates for the smallest and largest signal velocities. In the non-relativistic case, Einfeldt [81] proposed calculating them based on the smallest and largest eigenvalues of Roe’s matrix. The HLL scheme with Einfeldt’s recipe (HLLE) is a very robust upwind scheme for the Euler equations and possesses the property of being positively conservative. The HLLE method is exact for single shocks, but it is very dissipative, especially at contact discontinuities.

Schneider et al. [256] have presented results in 1D relativistic hydrodynamics using a relativistic version of the HLL method (RHLLE) with signal velocities given by

$${a_\text{R}} = \frac{{\bar v + {{\bar c}_\text{s}}}}{{1 + \bar v{{\bar c}_\text{s}}}},\;\;\;\;\;\;\;\;{a_\text{L}} = \frac{{\bar v - {{\bar c}_\text{s}}}}{{1 - \bar v{{\bar c}_\text{s}}}},$$

((51))

where c_s is the relativistic sound speed, and where the bar denotes the arithmetic mean between the initial left and right states. Duncan and Hughes [78] have generalized this method to 2D SRHD and applied it to the simulation of relativistic extragalactic jets.

3.7 Artificial wind method

The fact that classical hydrodynamic equations are Galilean invariant (Lorentz invariant in the relativistic case) is exploited in the artificial wind (AW) method [264]. One chooses a reference frame where the flow through zone interfaces is always supersonic. This reduces the problem of upwinding to a trivial task (avoiding the need of any spectral decomposition of the flux Jacobians). In case of the global AW method, the choice of the reference frame is global, whereas in case of the local AW method an appropriate choice is made at every numerical interface which reduces the numerical diffusion. Explicit expressions for the velocities of the reference frames (AW velocities) are given to ensure stability and to reduce diffusion. The resulting expressions for the numerical flux coincide formally with those of the HLL method. In the differential AW method, AW velocities are chosen as low as possible for each of the intermediate states between contiguous numerical zones obtained using weighted linear interpolations.

3.8 Marquina’s flux formula

Godunov-type schemes are indeed very robust in most situations although they fail spectacularly on occasions. Reports on approximate Riemann solver failures and their respective corrections (usually a judicious addition of artificial dissipation) are abundant in the literature [238]. Motivated by the search for a robust and accurate approximate Riemann solver that avoids these common failures, Donat and Marquina [76] have extended a numerical flux formula, which was first proposed by Shu and Osher [260] for scalar equations, to systems of equations. In the scalar case and for characteristic wave speeds which do not change sign at the given numerical interface, Marquina’s flux formula is identical to Roe’s flux. Otherwise, the scheme switches to the more viscous, entropy satisfying local Lax-Friedrichs scheme [260]. In the case of systems, the combination of Roe and local-Lax-Friedrichs solvers is carried out in each characteristic field after the local linearization and decoupling of the system of equations [76]. However, contrary to Roe’s and other linearized methods, the extension of Marquina’s method to systems is not based on any averaged intermediate state.

Martí et al. have used a version of Marquina’s method that applies the Lax-Friedrichs flux to all fields (modified Marquina’s flux formula) in their simulations of relativistic jets [182, 183]. The resulting numerical code has been successfully used to describe ultra-relativistic flows in both one and two spatial dimensions with great accuracy (a large set of test calculations using Marquina’s Riemann solver can be found in Appendix II of [183]). Numerical experimentation in two dimensions confirms that the dissipation of the scheme is sufficient to eliminate the carbuncle phenomenon [238], which appears in high Mach number relativistic jet simulations when using other standard solvers [75]. 2D Simulations of relativistic AGN jets using Marquina’s flux formula have also been performed by Mizuta et al. [196], the code being second-order accurate in space (MUSCL reconstruction [282]) and first-order accurate in time. Aloy et al. [6] have implemented the modified Marquina flux formula in their three-dimensional relativistic hydrodynamic code GENESIS. Font et al. [93] have developed a 3D general relativistic hydro code where the matter equations are integrated in conservation form and fluxes are calculated with Marquina’s formula.

3.9 Symmetric TVD, ENO schemes with nonlinear numerical dissipation

The methods discussed in Sections 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, and 3.8 are all based on exact or approximate solutions of Riemann problems at cell interfaces in order to stabilize the discretization scheme across strong shocks. Another successful approach relies on the addition of nonlinear dissipation terms to standard finite difference methods. The algorithm of Davis [68] is based on such an approach. It can be interpreted as a Lax-Wendroff scheme with a conservative TVD dissipation term. The numerical dissipation term is local, free of problem dependent parameters and does not require any characteristic information. This last fact makes the algorithm extremely simple when applied to any hyperbolic system of conservation laws.

A relativistic version of Davis’ method has been used by Koide et al. [138, 136, 210] in 2D and 3D simulations of relativistic magneto-hydrodynamic jets with moderate Lorentz factors. Although the results obtained are encouraging, the coarse grid zoning used in these simulations and the relative smallness of the beam flow Lorentz factor (4.56, beam speed ≈ 0.98c) does not allow for a comparison with Riemann-solver-based HRSC methods in the ultra-relativistic limit.

Davis’ method is second-order accurate in space and time. However, when simulating complex hydrodynamic and especially magneto-hydrodynamic flows, accuracy is an important issue. To this end Del Zanna and Bucciantini [71] have presented a global third order accurate, centered scheme for multi-dimensional SRHD. The basic properties of Del Zanna and Bucciantini’s method are based on the work of Liu and Osher [164]:

• the use of point values instead of cell averages,

• time integration with TVD Runge-Kutta methods, and

• third-order accurate ENO reconstruction algorithm.

To preserve the symmetric property of the method, monotonic high-order numerical fluxes are computed at zone interfaces by means of central-type Riemann solvers avoiding spectral decomposition (e.g., Lax-Friedrichs numerical flux). The authors also test the Riemann solver of Harten, Lax, and van Leer within the framework of non-biased Riemann solvers.

Recently, Anninos and Fragile [10] have developed a second order, non-oscillatory, central difference (NOCD) scheme for the numerical integration of the GRHD equations. The code uses MUSCL-type piecewise linear spatial interpolation to achieve second-order accuracy in space. Second-order accuracy in time is guaranteed by means of a predictor-corrector procedure. Symmetric numerical fluxes are evaluated after the predictor step. The results obtained in a series of challenging test problems (see Section 6) are encouraging.

4 Other Developments

4.1 Van Putten’s approach

Relying on a formulation of Maxwell’s equations as a hyperbolic system in divergence form, van Putten [285] has devised a numerical method to solve the equations of relativistic ideal MHD in flat spacetime [287]. Here we only discuss the basic principles of the method in one spatial dimension. In van Putten’s approach, the state vector u and the fluxes F of the conservation laws are decomposed into a spatially constant mean (subscript 0) and a spatially dependent variational (subscript 1) part,

$$u(t,x) = {u_0}(t) + {u_1}(t,x),\;\;\;\;\;\;\;F(t,x) = {F_0}(t) + {F_1}(t,x).$$

((52))

The RMHD equations then become a system of evolution equations for the integrated variational parts u₁*, which reads

$$\frac{{\partial {u_1}^*}}{{\partial t}} + {F_1} = 0,$$

((53))

together with the conservation condition

$$\frac{{d{F_0}}}{{dt}} = 0.$$

((54))

The quantities u₁* are defined as

$${u_1}^*(t,x) = {\smallint ^x}{u_1}(t,y)\;dy.$$

((55))

They are continuous, and standard methods can be used to integrate the system (53). Van Putten uses a leapfrog method.

The new state vector u(t, x) is then obtained from u₁*(t, x) by numerical differentiation. This process can lead to oscillations in the case of strong shocks and a smoothing algorithm should be applied. Details of this smoothing algorithm and of the numerical method in one and two spatial dimensions can be found in [286] together with results on a large variety of tests.

Van Putten has applied his method to simulate relativistic hydrodynamic and magneto-hydrodynamic jets with moderate flow Lorentz factors (< 4.25) [288, 291].

4.2 Relativistic SPH

Besides finite volume schemes, another completely different method is widely used in astrophysics for integrating the hydrodynamic equations. This method is Smoothed Particle Hydrodynamics, or SPH for short [168, 102, 199]. The fundamental idea of SPH is to represent a fluid by a Monte Carlo sampling of its mass elements. The motion and thermodynamics of these mass elements is then followed as they move under the influence of the hydrodynamic equations. Because of its Lagrangian nature there is no need within SPH for explicit integration of the continuity equation, but in some implementations of SPH for certain reasons this is nevertheless done. As both the equation of motion of the fluid and the energy equation involve continuous properties of the fluid and their derivatives, it is necessary to estimate these quantities from the positions, velocities and internal energies of the fluid elements, which can be thought of as particles moving with the flow. This is done by treating the particle positions as a finite set of interpolating points, where the continuous fluid variables and their gradients are estimated by an appropriately weighted average over neighboring particles. Hence, SPH is a free-Lagrange method, i.e., spatial gradients are evaluated without the use of a computational grid.

A comprehensive discussion of SPH can be found in the reviews of Hernquist and Katz [124], Benz [20], and Monaghan [198, 199]. The non-relativistic SPH equations are briefly discussed in Section 9.6. The capabilities and limits of SPH are explored, e.g., in [269, 16, 167, 275], and the stability of the SPH algorithm is investigated in [271].

The SPH equations for special relativistic flows have been first formulated by Monaghan [198]. Monaghan and Price [202] showed how the equations of motion for the SPH method may be derived from a variational principle for both non-relativistic and (special and general) relativistic flows when there is no dissipation. For relativistic flows the SPH equations given in Section 9.6 can be used except that each SPH particle a carries v_a baryons instead of mass m_a [198, 53]. Hence, the rest mass of particle a is given by m_a = m₀v_a, where m₀ is the baryon rest mass (if the fluid is made of baryons). Transforming the notation used in [53] to ours, the continuity equation, the momentum, and the total energy equations for particle a are given by (unit of velocity is c)

$$\frac{{d{N_a}}}{{dt}} = - \sum\limits_b {{v_b}({v_a} - {v_b}) \cdot {\nabla _a}{W_{ab}},} $$

((56))

$$\frac{{d{{\hat S}_a}}}{{dt}} = - \sum\limits_b {{v_b}\left( {\frac{{{p_a}}}{{N_a^2}} + \frac{{{p_b}}}{{N_b^2}} + {\prod _{ab}}} \right) \cdot {\nabla _a}{W_{ab}},} $$

((57))

and

$$\frac{{d{{\hat \tau }_a}}}{{dt}} = - \sum\limits_b {{v_b}\left( {\frac{{{p_a}{v_a}}}{{N_a^2}} + \frac{{{p_b}{v_b}}}{{N_b^2}} + {\Omega _{ab}}} \right) \cdot {\nabla _a}{W_{ab}},} $$

((58))

respectively. Here, the summation is over all particles other than particle a, and d/dt denotes the Lagrangian time derivative.

$$N = \frac{D}{{{m_0}}}$$

((59))

is the baryon number density,

$$\hat S \equiv \frac{\text{S}}{N} = {m_0}hW\text{v}$$

((60))

is the momentum per particle, and

$$\hat \tau \equiv \frac{\tau }{N} + {m_0} = {m_0}hW - \frac{p}{N}$$

((61))

is the total energy per particle (all measured in the laboratory frame). The momentum density S ≡ (S¹, S², S³)^T , the energy density τ (measured in units of the rest mass energy density), and the specific enthalpy h are defined in Section 2.1. Π_ab and Ω_ab are the SPH dissipation terms, and ∇_aW_ab denotes the gradient of the kernel W_ab (see Section 9.6 for more details).

Special relativistic flow problems have been simulated with SPH by [151, 134, 172, 174, 53, 261]. Extensions of SPH capable of treating general relativistic flows have been considered by [134, 150, 261, 202, 204]. Concerning relativistic SPH codes the artificial viscosity is the most critical issue. It is required to handle shock waves properly, and ideally it should be predicted by a relativistic kinetic theory for the fluid. However, unlike its Newtonian analogue, the relativistic theory has not yet been developed to the degree required to achieve this.

For Newtonian SPH, Lattanzio et al. [155] have shown that a viscosity quadratic in the velocity divergence is necessary in high Mach number flows. They proposed a form such that the viscous pressure could be simply added to the fluid pressure in the equation of motion and the energy equation. As this simple form of the artificial viscosity has known limitations, they also proposed a more sophisticated form of the artificial viscosity terms, which leads to a modified equation of motion. This artificial viscosity works much better, but it cannot be generalized to the relativistic case in a consistent way. Utilizing an equation for the specific internal energy, both Mann [172] and Laguna et al. [150] use such an inconsistent formulation. Their artificial viscosity term is not included in the expression of the specific relativistic enthalpy. In a second approach, Mann [172] allows for a time-dependent smoothing length and SPH particle mass, and further proposes an SPH variant based on the total energy equation. Lahy [151] and Siegler and Riffert [261] use a consistent artificial viscosity pressure added to the fluid pressure. Siegler and Riffert [261] have also formulated the hydrodynamic equations in conservation form (see also [202]).

Monaghan [200] incorporates concepts from Riemann solvers into SPH (see also [129]). For this reason he also proposes to use a total energy equation in SPH simulation instead of the commonly used internal energy equation, which would involve time derivatives of the Lorentz factor in the relativistic case. Chow and Monaghan [53] have extended this concept and have proposed an SPH algorithm, which gives good results when simulating an ultra-relativistic gas. In both cases the intention was not to introduce Riemann solvers into the SPH algorithm, but to use them as a guide to improve the artificial viscosity required in SPH. Multi-dimensional simulations of general relativistic flows (in a given time-independent metric) using the SPH formulation of Monaghan and Price [202] and the SPH algorithm of Chow and Monaghan [53] have been performed by Muir [204].

In Roe’s Riemann solver [247], as well as in its relativistic variant proposed by Eulerdink [83, 84] (see Section 3.4), the numerical flux is computed by solving a locally linear system, and depends on both the eigenvalues and (left and right) eigenvectors of the Jacobian matrix associated to the fluxes and on the jumps in the conserved physical variables (see Equations (36) and (37)). Monaghan [200] realized that an appropriate form of the dissipative terms Π_ab and Ω_ab for the interaction between particles a and b can be obtained by treating the particles as the equivalent of left and right states taken with reference to the line joining the particles. The quantity corresponding to the eigenvalues (wave propagation speeds) is an appropriate signal velocity v_sig (see below), and that equivalent to the jump across characteristics is a jump in the relevant physical variable. For the artificial viscosity tensor, Π_ab, Monaghan [200] assumes that the jump in velocity across characteristics can be replaced by the velocity difference between a and b along the line joining them.

With these considerations in mind, Chow and Monaghan [53] proposed for Π_ab in the relativistic case the form

$${\Pi _{ab}} = - \frac{{K{v_{\text{sig}}}(\hat S_a^* - \hat S_b^*) \cdot \text{j}}}{{{{\bar N}_{ab}}}}$$

((62))

when particles a and b are approaching, and Π_ab = 0 otherwise. Here K = 0.5 is a dimensionless parameter, which is chosen to have the same value as in the non-relativistic case [200]. ${\bar N_{ab}} = ({N_a} + {N_b})/2$ is the average baryon number density, which has to be present in Equation (62), because the pressure terms in the summation of Equation (101) (see Section 9.6) have an extra density in the denominator arising from the SPH interpolation. Furthermore,

$$\text{j} = \frac{{{\text{r}_{ab}}}}{{\left| {{\text{r}_{ab}}} \right|}}$$

((63))

is the unit vector from b to a, and

$${\hat {\text{S}}^*} = {m_0}h{W^*}\text{v},$$

((64))

where

$${W^*} = \frac{1}{{\sqrt { - {{(\text{v} \cdot \text{j})}^2}} }}.$$

((65))

Using instead of $\hat S$ (see Equation (60)) the modified momentum ${\hat S^*}$, which involves the line of sight velocity v · j, guarantees that the viscous dissipation is positive definite [53].

The dissipation term in the energy equation is derived in a similar way, and is given by [53]

$${\Omega _{ab}} = - \frac{{K{v_{sig}}(\hat \tau _a^* - \hat \tau _b^*)\text{j}}}{{{{\bar N}_{ab}}}},$$

((66))

if a and b are approaching, and Ω_ab = 0 otherwise. Ω_ab involves the energy ${\hat \tau ^*}$, which is identical to $\hat \tau$ (see Equation (61)) except that W is replaced by W*.

To determine the signal velocity, Chow and Monaghan [53] (and Monaghan [200] in the non-relativistic case) start from the (local) eigenvalues, and hence the wave velocities (v ± C_s)/(1 ± vc_s) and v of one-dimensional relativistic hydrodynamic flows. Again considering particles a and b as the left and right states of a Riemann problem with respect to motions along the line joining the particles, the appropriate signal velocity is the speed of approach (as seen in the computing frame) of the signal sent from a towards b and that from b to a. This is the natural speed for the sharing of physical quantities, because when information about the two states meets it is time to construct a new state. This speed of approach should be used when determining the size of the time step by the Courant condition (for further details see [53]).

Chow and Monaghan [53] have demonstrated the performance of their Riemann problem guided relativistic SPH algorithm by calculating several shock tube problems involving ultra-relativistic speeds up to v = 0.9999. The algorithm gives good results, but finite volume schemes based on Riemann solvers give more accurate results and can handle even larger speeds (see Section 6).

4.3 Relativistic beam scheme

Sanders and Prendergast [253] proposed an explicit scheme to solve the equilibrium limit of the non-relativistic Boltzmann equation, i.e., the Euler equations of Newtonian fluid dynamics. In their so-called beam scheme the Maxwellian velocity distribution function is approximated by several Dirac delta functions or discrete beams of particles in each computational cell, which reproduce the appropriate moments of the distribution function. The beams transport mass, momentum, and energy into adjacent cells, and their motion is followed to first-order accuracy. The new (i.e., time advanced) macroscopic moments of the distribution function are used to determine the new local non-relativistic Maxwell distribution in each cell. The entire process is then repeated for the next time step. The CFL stability condition requires that no beam of gas travels farther than one cell in one time step. This beam scheme, although being a particle method derived from a microscopic kinetic description, has all the desirable properties of modern characteristic-based wave propagating methods based on a macroscopic continuum description.

The non-relativistic scheme of Sanders and Prendergast [253] has been extended to relativistic flows by Yang et al. [303]. They replaced the Maxwellian distribution function by its relativistic analogue, i.e., by the more complex Juttner distribution function, which involves modified Bessel functions. For three-dimensional flows the Juttner distribution function is approximated by seven delta functions or discrete beams of particles, which can viewed as dividing the particles in each cell into seven distinct groups. In the local rest frame of the cell these seven groups represent particles at rest and particles moving in ±x, ±y, and ±z directions, respectively.

Yang et al. [303] show that the integration scheme for the beams can be cast into the form of an upwind conservation scheme in terms of numerical fluxes. They further show that the beam scheme not only splits the state vector but also the flux vectors, and has some entropy-satisfying mechanism embedded as compared with an approximate relativistic Riemann solver [74, 256] based on Roe’s method [247]. The simplest relativistic beam scheme is only first-order accurate in space, but can be extended to higher-order accuracy in a straightforward manner. Yang et al. consider three high-order accurate variants (TVD2, ENO2, ENO3) generalizing their approach developed in [304, 305] for Newtonian gas dynamics, which is based on the essentially non-oscillatory (ENO) piecewise polynomial reconstruction scheme of Harten et al. [120].

Yang et al. [303] present several numerical experiments including relativistic one-dimensional shock tube flows and the simulation of relativistic two-dimensional Kelvin-Helmholtz instabilities. The shock tube experiments consist of a mildly relativistic shock tube, relativistic shock heating of a cold flow, the relativistic blast wave interaction of Woodward and Colella [300] (see Section 6.2.3), and the perturbed relativistic shock tube flow of Shu and Osher [260].

5 Summary of Methods

This section contains a summary of all the methods reviewed in the two preceding Sections 3 and 4 as well as several FCT and artificial viscosity codes. The main characteristic of the codes (dissipation algorithm, spatial and temporal orders of accuracy, reconstruction techniques) are listed in three table:

• Table 3 for HRSC codes using characteristic information,

• Table 4 for HRSC codes avoiding the use of such information, and

• Table 5 for other approaches.

Table 3 High-resolution shock-capturing methods using characteristic information. All the codes rely on a conservation form of the RHD equations with the exception of [295].

Table 4 High-resolution shock-capturing methods avoiding the use of characteristic information.

Table 5 Code characteristics

6 Test Bench

6.1 Relativistic shock heating in planar, cylindrical and spherical geometry

Shock heating of a cold fluid in planar, cylindrical, or spherical geometry has been used since the early developments of numerical relativistic hydrodynamics as a test case for hydrodynamic codes, because it has an analytical solution ([26] in planar symmetry, [183] in cylindrical and spherical symmetry), and because it involves the propagation of a strong relativistic shock wave.

In planar geometry, an initially homogeneous, cold (i.e., ε ≈ 0) gas with coordinate velocity v₁ and Lorentz factor W₁ is supposed to hit a wall, while in the case of cylindrical and spherical geometry the gas flow converges towards the axis or the center of symmetry. In all three cases the reflection causes compression and heating of the gas as kinetic energy is converted into internal energy. This occurs in a shock wave, which propagates upstream. Behind the shock the gas is at rest (v₂ = 0). Due to conservation of energy across the shock, the gas has a specific internal energy given by

$${\varepsilon _2} = {W_1} - 1.$$

((67))

The compression ratio σ of shocked and unshocked gas follows from

$$\sigma = \frac{{\gamma + 1}}{{\gamma - 1}} + \frac{\gamma }{{\gamma - 1}}{\varepsilon _2},$$

((68))

where γ is the adiabatic index of the equation of state. The shock velocity is given by

$${V_s} = \frac{{(\gamma - 1){W_1}\left| {{v_1}} \right|}}{{{W_1} + 1}}.$$

((69))

In the unshocked region (r ∈ [V_st, ∞) the pressure-less gas flow is self-similar and has a density distribution given by

$$\rho (t,r) = {\left( {1 + \frac{{\left| {{v_1}} \right|t}}{r}} \right)^\alpha }{\rho _0},$$

((70))

where α = 0, 1, 2 for planar, cylindrical, or spherical geometry, and where ρ₀ is the density of the inflowing gas at infinity (see Figure 5).

In the Newtonian case the compression ratio σ of shocked and unshocked gas cannot exceed a value of σ_max = (γ+1)/(γ-1) independently of the inflow velocity. This is different for relativistic flows, where σ grows linearly with the flow Lorentz factor and becomes infinite as the inflowing gas velocity approaches to speed of light.

The maximum flow Lorentz factor achievable for a hydrodynamic code with acceptable errors in the compression ratio o- is a measure of the code’s quality. Table 6 contains a summary of the results obtained for the shock heating test by various authors.

Explicit finite difference techniques based on a non-conservative formulation of the hydrodynamic equations and on non-consistent artificial viscosity [50, 123, 10] (or even consistent artificial viscosity [10]) are able to handle flow Lorentz factors up to ≈ 10 with moderately large errors (σ_error ≈ 1–3%) at best [298, 187]. Norman and Winkler [213] got very good results (σ_error ≈ 0.01%) for a flow Lorentz factor of 10 using consistent artificial viscosity terms and an implicit adaptive mesh method.

The performance of explicit codes improved significantly when numerical methods based on Riemann solvers were introduced [179, 176, 83, 256, 84, 181, 89]. More recently, HRSC methods based on symmetric discretizations [71, 10] have also demonstrated the same capability to describe highly relativistic flows. For some of these codes the maximum flow Lorentz factor is only limited

Figure 5

Schematic solution of the shock heating problem in spherical geometry. The initial state consists of a spherically symmetric flow of cold (p = 0) gas of unit rest mass density having a highly relativistic inflow velocity everywhere. A shock is generated at the center of the sphere, which propagates upstream with constant speed. The post-shock state is constant and at rest. The pre-shock state, where the flow is self-similar, has a density which varies as ρ = (1 + t/r)² with time t and radius r.

by the precision by which numbers are represented on the computer used for the simulation [74, 295, 6, 10].

Schneider et al. [256] have compared the accuracy of a code based on the RHLLE Riemann solver with different versions of relativistic FCT codes for inflow Lorentz factors in the range 1.5 to 50. They find that the error in a is reduced by a factor of two when using HLL. Further tests of the (1D) RHLLE method were performed by Rischke et al. [244, 246, 245] who considered expansion into vacuum, semi-infinite colliding slabs, and spherically and cylindrically symmetric expansions for equations of state for both thermodynamically normal and anomalous matter (see Section 7.3). In the latter two test cases RHLLE transport is done in the radial direction while corrections due to geometry are implemented via Sod’s method. Rischke et al. [244, 246] also present a detailed comparison of the RHLLE method and relativistic extensions [113] of flux-corrected transport (FCT) algorithms [33, 35, 34]. They find that not all versions of the numerical algorithms explored in their investigation can be straightforwardly applied. Moreover, numerical parameters like the grid spacing or the antidiffusion coefficients (for FCT SHASTA) must be chosen with care, in order to produce solutions which are free of numerical artifacts. Studying the “slab-on-slab” collision test problem (up to flow Lorentz factors of 2.3) they particularly find [246] that analytical solutions are reproduced remarkably well with RHLLE and also with FCT SHASTA, provided the numerical diffusion is sufficiently large (i.e., when the antidiffusion in SHASTA is chosen sufficiently small).

Within SPH methods, Chow and Monaghan [53] have obtained results comparable to those of HRSC methods (σ_error < 2 × 10⁻³) for flow Lorentz factors up to 70, using a relativistic SPH code with Riemann solver guided dissipation. Sieglert and Riffert [261] have succeeded in reproducing the post-shock state accurately for inflow Lorentz factors of 1000 with a code based on a consistent formulation of artificial viscosity. However, the dissipation introduced by SPH methods at the shock transition is very large (10–12 particles in the code of [261]; 20–24 in the code of [53]) compared with the typical dissipation of HRSC methods (see below).

The performance of a HRSC method based on a relativistic Riemann solver is illustrated by means of an MPEG movie (Figure 6) for the planar shock heating problem for an inflow velocity v₁ = −0.99999c (W₁ ≈ 223). These results are obtained with the relativistic code rPPM used in [181] and provided in Section 9.4.3.

The shock wave is resolved by three zones and there are no post-shock numerical oscillations. The density increases by a factor ≈ 900 across the shock. Near x = 0 the density distribution slightly undershoots the analytical solution (by ≈ 8%) due to the numerical effect of wall heating. The profiles obtained for other inflow velocities are qualitatively similar. The mean relative error of the compression ratio Uerror is smaller than 10-3, and, in agreement with other codes based on a Riemann solver, the accuracy of the results does not exhibit any significant dependence on the Lorentz factor of the inflowing gas. The quality of the results obtained with high-order symmetric schemes [10, 71] is similar.

Some authors have considered the problem of shock heating in cylindrical or spherical geometry using adapted coordinates to test the numerical treatment of geometrical factors [249, 183, 295]. Aloy et al. [6] have considered the spherically symmetric shock heating problem in 3D Cartesian coordinates as a test case for both the directional splitting and the symmetry properties of their code GENESIS. The code is able to handle this test up to inflow Lorentz factors of the order of 700.

In the shock reflection test, conventional schemes often give numerical approximations which exhibit a consistent O(1) error for the density and internal energy in a few cells near the reflecting wall. This ‘overheating’, as it is known in classical hydrodynamics [212], is a numerical artifact which is considerably reduced when Marquina’s scheme is used [76]. In passing we note that the strong overheating found by Noh [212] for the spherical shock reflection test using PPM (Figure 24 in [212]) is not a problem of PPM, but of his implementation of PPM. When properly implemented, PPM gives a density undershoot near the origin of about 9% in case of a non-relativistic flow. The piece-wise linear method described in [249] gives an undershoot of 14% in case of ultra-relativistic flows (e.g., Table 1 and Figure 1 in [249]).

Table 6 Summary of relativistic shock heating test calculations by various authors in planar (α = 0), cylindrical (α = 1), and spherical (α = 2) geometry. W_max and σ_error are the maximum inflow Lorentz factor and compression ratio error extracted from tables and figures of the corresponding reference. W_max should only be considered as indicative of the maximum Lorentz factor achievable by the respective method. Methods are described in Sections 3 and 4, and their basic properties are summarized in Section 5 (Tables 3, 4, and 5).

Figure 6

mpg-Movie (711 KB) Still from a MPEG movie showing the evolution of the density distribution for the shock heating problem with an inflow velocity v₁ = -0.99999c in Cartesian coordinates. The reflecting wall is located at x = 0. The adiabatic index of the gas is 4/3. For numerical reasons, the specific internal energy of the inflowing cold gas is set to a small finite value (ε₁ = 10⁻⁷W₁). The final frame of the movie also shows the analytical solution (blue lines). The simulation has been performed on an equidistant grid of 100 zones. >(For video see appendix)

6.2 Propagation of relativistic blast waves

Riemann problems with large initial pressure jumps produce blast waves with dense shells of material propagating at relativistic speeds (see Figure 7). For appropriate initial conditions, both the speed of the leading shock front and the velocity of the shell material approach the speed of light producing very narrow structures. The accurate description of these thin, relativistic shells involving large density contrasts is a challenge for any numerical code. Some particular blast wave problems have become standard numerical tests. Here we consider the two most common of these tests. The initial conditions are given in Table 7.

Figure 7

Generation and propagation of a relativistic blast wave (schematic). The large pressure jump at a discontinuity initially located at r = 0.5 gives rise to a blast wave and a dense shell of material propagating at relativistic speeds. For appropriate initial conditions both the speed of the leading shock front and the velocity of the shell approach the speed of light, producing very narrow structures.

Table 7 Initial data (pressure p, density ρ, velocity v) for two common relativistic blast wave test problems. The decay of the initial discontinuity leads to a shock wave (velocity v_shock, compression ratio σ_shock) and the formation of a dense shell (velocity v_shell, time-dependent width w_shell) both propagating to the right. The gas is assumed to be ideal with an adiabatic index γ = 5/3.

Problem 1 was a demanding problem for relativistic hydrodynamic codes in the mid-eighties [50, 123], while Problem 2 is a challenge even for today’s state-of-the-art codes. The analytical solution of both problems can be obtained with program RIEMANN (see Section 9.4).

6.2.1 Problem 1

In Problem 1, the decay of the initial discontinuity gives rise to a dense shell of matter with velocity v_shell = 0.72 (W_shell = 1.38) propagating to the right. The shell trailing a shock wave of speed v_shock = 0.83 increases its width w_shell according to w_shell = 0.11t, i.e., at time t = 0.4 the shell covers about 4% of the grid (0 ≤ x ≤ 1). Tables 8 and 9 give a summary of the references where this test was considered for non-HRSC and HRSC methods, respectively.

Using artificial viscosity techniques, Centrella and Wilson [50] were able to reproduce the analytical solution with a 7% overshoot in vshell, whereas Hawley et al. [123] found a 16% error in the shell density. However, when implementing a consistent formulation of artificial viscosity, like in the method developed by Anninos and Fragile [10], it is possible to capture the constant states in a stable manner and without noticeable errors (e.g., the shell density is underestimated by less than 2%).

The results obtained with early relativistic SPH codes [172] were affected by systematic errors in the rarefaction wave and the constant states, large amplitude spikes at the contact discontinuity, and large smearing. Smaller systematic errors and spikes are obtained with Laguna et al.’s (1993) code [150]. This code also leads to a large density overshoot in the shell. Much cleaner states are obtained with the methods of Chow and Monaghan (1997) [53] and Siegler and Riffert (1999) [261], both based on conservative formulations of the SPH equations. For Chow and Monaghan’s (1997) method [53] the spikes at the contact discontinuity disappear but at the cost of an excessive smearing. This smearing can also be observed in Muir [204] (see Figures 8 and 9), who used the general relativistic, conservative SPH formulation of Monaghan and Price [202], and the dissipation method of Chow and Monaghan [53] to simulate Problem 1 assuming a Minkowski spacetime. Generally speaking, shock profiles obtained with relativistic SPH codes are smeared out more than those computed with HRSC methods, the shocks modelled by SPH typically being covered by more than 10 zones.

Van Putten has considered a similar initial value problem with somewhat more extreme conditions (v_shell ≈ 0.82c, σ_shock ≈ 5.1) and with a transversal magnetic field. For suitable choices of the smoothing parameters his results are accurate and stable, although discontinuities appear to be more smeared than with typical HRSC methods (6–7 zones for the strong shock wave; ≈ 50 zones for the contact discontinuity).

Table 8 Summary of references where the blast wave problem 1 (defined in Table 7) has been considered in 1D, 2D and, 3D, respectively. Methods are described in Sections 3 and 4, and their basic properties are summarized in Section 5 (Tables 3, 4, and 5). Note that CD stands for contact discontinuity.

Table 9 Summary of references where the blast wave Problem 1 (defined in Table 7) has been considered in 1D, 2D, and 3D, respectively. Methods are described in Sections 3 and 4, and their basic properties are summarized in Section 5 (Tables 3, 4, and 5). Note that CD stands for contact discontinuity.

Figure 8

Density distribution for the relativistic blast wave Problem 1 defined in Table 7 at t=0.314 obtained with the code SPH-RS-gr (see Table 5) of Muir [204] using 5500 SPH particles and a 1D version of the code. The solid lines give the exact solutions.

Figure 9

Velocity distribution for the relativistic blast wave Problem 1 defined in Table 7 at t=0.314 obtained with the code SPH-RS-gr (see Table 5) of Muir [204] using 5500 SPH particles and a 1D version of the code. The solid lines give the exact solutions.

An MPEG movie (Figure 10) shows the Problem 1 blast wave evolution obtained with a modern HRSC method (the relativistic PPM method introduced in Section 3.1; code rPPM provided in Section 9.4.3). The grid has 400 equidistant zones, and the relativistic shell is resolved by 16 zones. Because of both the high-order accuracy of the method in smooth regions and its small numerical diffusion (the shock is resolved with 4–5 zones only) the density of the shell is accurately computed (errors less than 0.1%). Other codes based on relativistic Riemann solvers [84] or symmetric high-order discretizations (specially the third-order schemes in [71]) give similar results (see Table 9). The RHLLE method [256] underestimates the density in the shell by about 10% in a 200 zone calculation.

Figure 10

mpg-Movie (456 KB) Still from a MPEG movie showing the evolution of the density distribution for the relativistic blast wave Problem 1 defined in Table 7. The final frame of the movie also shows the analytical solution (blue lines. The simulation has been performed with relativistic PPM on an equidistant grid of 400 zones. (For video see appendix)

6.2.2 Problem 2

Problem 2 was first considered by Norman and Winkler [213]. The flow pattern is similar to that of Problem 1, but more extreme. Relativistic effects reduce the post-shock state to a thin dense shell with a width of only about 1% of the grid length at t = 0.4. The fluid in the shell moves with vshell = 0.960 (i.e., W_shell = 3.6), while the leading shock front propagates with a velocity v_shock = 0.986 (i.e., W_shock = 6.0). The jump in density in the shell reaches a value of 10.6. Norman and Winkler [213] obtained very good results with an adaptive grid of 400 zones using an implicit hydrodynamics code with artificial viscosity. Their adaptive grid algorithm placed 140 zones of the available 400 zones within the blast wave, thereby accurately capturing all features of the solution.

Several HRSC methods based on relativistic Riemann solvers have used Problem 2 as a standard test [179, 176, 181, 89, 295, 75]. More recently, some symmetric HRSC codes [71, 10] have also considered this problem reporting results which are competitive (as in the case of the algorithms described in [71]) with those obtained with Riemann solver based schemes. Table 10 gives a summary of the references where this test was considered.

Table 10 Summary of references where the blast wave problem 2 (defined in Table 7) has been considered. Shock compression ratios or are evaluated for runs with 400 numerical zones and at t ≈ 0.40, unless otherwise established. Methods are described in Sections 3 and 4, and their basic properties are summarized in Section 5 (Tables 3, 4, and 5).

An MPEG movie (Figure 11) shows the Problem 2 blast wave evolution obtained with the relativistic PPM method introduced in Section 3.1) on a grid of 2000 equidistant zones. At this resolution the relativistic PPM code obtains a converged solution. The method of Falle and Komissarov [89] requires a seven level adaptive grid calculation to achieve the same, the finest grid spacing corresponding to a grid of 3200 zones. As their code is free of numerical diffusion and dispersion, Wen et al. [295] are able to handle this problem with high accuracy (see Figure 12). At lower resolution (400 zones) the relativistic PPM method reaches only 69% of the theoretical shock compression value (54% in case of the second-order accurate upwind method of Falle and Komissarov [89]; 60% with the code of Donat et al. [75]).

Figure 11

mpg-Movie (1.41 MB) Still from a MPEG movie showing the evolution of the density distribution for the relativistic blast wave Problem 2 defined in Table 7. The final frame of the movie also shows the analytical solution (blue lines. The simulation has been performed with relativistic PPM on an equidistant grid of 2000 zones. (For video see appendix)

Figure 12

Results from [295] for the relativistic blast wave Problems 1 (left column and Problem 2 (right column, respectively. Relativistic Glimm’s method is only used in regions with steep gradients. Standard finite difference schemes are applied in the smooth remaining part of the computational domain. In the above plots, Lax and LW stand for Lax and Lax-Wendroff methods, respectively; G refers to pure Glimm’s method.

Chow and Monaghan [53] have considered Problem 2 to test their relativistic SPH code. Besides a 15% overshoot in the shell’s density, the code produces a non-causal blast wave propagation speed (i.e., v_shock > 1).

Anninos and Fragile [10] have considered Problem 2 as a test case for their artificial-viscosity based, explicit codes. They find a 40% overshoot in the shock density contrast. This demonstrates that the extra coupling introduced in the equations when using a consistent formulation of the artificial viscosity requires the usage of implicit algorithms.

6.2.3 Collision of two relativistic blast waves

The collision of two strong blast waves was used by Woodward and Colella [300] to compare the performance of several numerical methods in classical hydrodynamics. In the relativistic case, Yang et al. [303] considered this problem to test the high-order extensions of the relativistic beam scheme, whereas Martí and Müller [181] used it to evaluate the performance of their relativistic PPM code. In this last case, the original boundary conditions were changed (from reflecting to outflow) to avoid the reflection and subsequent interaction of rarefaction waves allowing for a comparison with an analytical solution. In the following we summarize the results on this test obtained by Martí and Müller in [181].

The initial data corresponding to this test, consisting of three constant states with large pressure jumps at the discontinuities separating the states (at x = 0.1 and x = 0.9), as well as the properties of the blast waves created by the decay of the initial discontinuities, are listed in Table 11. The propagation velocity of the two blast waves is slower than in the Newtonian case, but very close to the speed of light (0.9776 and −0.9274 for the shock wave propagating to the right and left, respectively). Hence, the shock interaction occurs later (at t = 0.420) than in the Newtonian problem (at t = 0.028). The top panel in Figure 13 shows four snapshots of the density distribution including the moment of the collision of the blast waves at t = 0.420 and x = 0.5106. At the time of collision the two shells have a width of Δx = 0.008 (left shell) and Δx = 0.019 (right shell), respectively, i.e., the entire interaction takes place in a very thin region (about 10 times smaller than in the Newtonian case where Δx ≈ 0.2).

Table 11 Initial data (pressure p, density ρ, velocity v) for the two relativistic blast wave collision test problem. The decay of the initial discontinuities (at x = 0.1 and x = 0.9) produces two shock waves (velocitis v_shock, compression ratios σ_shock) moving in opposite directions followed by two trailing dense shells (velocities v_shell, time-dependent widths w_shell). The gas is assumed to be ideal with an adiabatic index γ = 1.4.

Figure 13

The top panel shows a sequence of snapshots of the density profile for the colliding relativistic blast wave problem up to the moment when the waves begin to interact. The density profile of the new states produced by the interaction of the two waves is shown in the bottom panel (note the change in scale on both axes with respect to the top panel.

The collision gives rise to a narrow region of very high density (see lower panel of Figure 13) bounded by two shocks moving at speeds 0.088 (shock at the left) and 0.703 (shock at the right) and large compression ratios (7.26 and 12.06, respectively) well above the classical limit for strong shocks (6.0 for γ = 1.4). The solution just described applies until t = 0.430, when the next interaction takes place.

The complete analytical solution before and after the collision up to time t = 0.430 can be obtained following Appendix II in [181].

An MPEG movie (Figure 14) shows the evolution of the density up to the time of shock collision at t = 0.4200. The movie was obtained with the relativistic PPM code of Martí and Müller [181].

Figure 14

mpg-Movie (2.00 MB) Still from a MPEG movie showing the evolution of the density distribution for the colliding relativistic blast wave problem up to the interaction of the waves. The final frame of the movie also shows the analytical solution (blue lines. The computation has been performed with relativistic PPM on an equidistant grid of 4000 zones. (For video see appendix)

The presence of very narrow structures involving large density jumps requires very fine zoning to resolve the states properly. For the movie a grid of 4000 equidistant zones was used. The relative error in the density of the left (right) shell is always less than 2.0% (0.6%), and is about 1.0% (0.5%) at the moment of shock collision. Profiles obtained with the relativistic Godunov method (first-order accurate, not shown) show relative errors in the density of the left (right) shell of about 50% (16%) at t = 0.20. The errors drop only slightly to about 40% (5%) at the time of collision (t = 0.420).

An MPEG movie (Figure 15) shows the numerical solution after the interaction has occurred. Compared to the other MPEG movie (Figure 14), a very different scaling for the x-axis had to be used to display the narrow dense new states produced by the interaction. Obviously, the relativistic PPM code resolves the structure of the collision region satisfactorily well, the maximum relative error in the density distribution being less than 2.0%. When using the first-order accurate Godunov method instead, the new states are strongly smeared out, and the positions of the leading shocks are wrong.

Figure 15

mpg-Movie (697 KB) Still from a MPEG movie showing the evolution of the density distribution for the colliding relativistic blast wave problem around the time of interaction of the waves at an enlarged spatial scale. The final frame of the movie also shows the analytical solution (blue lines. The computation has been performed with relativistic PPM on an equidistant grid of 4000 zones. (For video see appendix)

7 Applications

7.1 Astrophysical jets

The most compelling case for a special relativistic phenomenon are the ubiquitous jets in extragalactic radio sources associated with active galactic nuclei. In the commonly accepted standard model [17], flow velocities as large as 99% of the speed of light (and in some cases even beyond) are required to explain the apparent superluminal motion observed at parsec scales in many of these sources. Models which have been proposed to explain the formation of relativistic jets involve accretion onto a compact central object, such as a neutron star or stellar mass black hole in the galactic micro-quasars GRS 1915+105 [195] and GRO J1655-40 [277], or a rotating supermassive black hole in an active galactic nucleus, which is fed by interstellar gas and gas from tidally disrupted stars.

Inferred jet velocities close to the speed of light suggest that jets are formed within a few gravitational radii of the event horizon of the black hole. Moreover, very-long-baseline interferometric (VLBI) radio observations reveal that jets are already collimated at subparsec scales [133, 178]. Current theoretical models assume that accretion disks are the source of the bipolar outflows which are further collimated and accelerated via MHD processes [41, 48, 190]. There is a large number of parameters which are potentially important for jet powering: the black hole mass and spin, the accretion rate and the type of accretion disk, the properties of the magnetic field and of the environment [193, 189].

At parsec scales, the jets, observed via their synchrotron and inverse Compton emission at radio frequencies with VLBI imaging, appear to be highly collimated with a bright spot (the core) at one end of the jet and a series of components which separate from the core, sometimes at superluminal speeds [108]. In the standard model [25], these speeds are interpreted as a consequence of relativistic bulk motions in jets propagating at small angles to the line of sight with Lorentz factors up to 20 or more. Moving components in these jets, usually preceded by outbursts in emission at radio wavelengths, are interpreted in terms of traveling shock waves [177].

Finally, the morphology and dynamics of jets at kiloparsec scales are dominated by the interaction of the jet with the surrounding extragalactic medium, the jet power being responsible for dichotomic morphologies [38] (the so called Fanaroff-Riley I and II classes [90], FR I and FR II, respectively). While current models [22, 152] interpret FR I morphologies as the result of a smooth deceleration from relativistic to non-relativistic, transonic speeds on kiloparsec scales due to a slower shear layer, flux asymmetries between jets and counter-jets in the most powerful radio galaxies (FR II) and quasars indicate that relativistic motion extends up to kiloparsec scales in these sources, although with smaller values of the overall bulk speeds [37]. The detection of strong X-ray emission from jets at large scales (0.1–1 Mpc; e.g., PKS0637-752 [51]) by the Chandra satellite, interpreted as scattered CMB radiation [49], bears additional support to the hypothesis of relativistic bulk speeds on these scales.

Although MHD and general relativistic effects seem to be crucial for a successful launch of the jet, purely hydrodynamic, special relativistic simulations are adequate to study the morphology and dynamics of relativistic jets at distances sufficiently far from the central compact object (i.e., at parsec scales and beyond). The development of relativistic hydrodynamic codes based on HRSC techniques (see Sections 3 and 4) has triggered the numerical simulation of relativistic jets at parsec and kiloparsec scales.

At kiloparsec scales, the implications of relativistic flow speeds and/or relativistic internal energies for the morphology and dynamics of jets have been the subject of a number of papers in recent years [184, 78, 182, 183, 148]. Beams with large internal energies show little internal structure and relatively smooth cocoons allowing the terminal shock (the hot spot in the radio maps) to remain well defined during the evolution. Their morphologies resemble those observed in naked quasar jets like 3C273 [67]. Figure 16 shows several snapshots of the time evolution of a light, relativistic jet with large internal energy. The dependence of the beam’s internal structure on the flow speed suggests that relativistic effects may be relevant for the understanding of the difference between slower, knotty BL Lac jets and faster, smoother quasar jets [97].

Figure 16

Time evolution of a light, relativistic (beam flow velocity equal to 0.99 jet with large internal energy. The logarithm of the proper rest mass density is plotted in grey scale, the maximum value corresponding to white and the minimum to black.

Highly supersonic models, in which kinematic relativistic effects due to high beam Lorentz factors dominate, have extended over-pressured cocoons. These over-pressured cocoons can help to confine the jets during the early stages of their evolution [182], and even cause their deflection when propagating through non-homogeneous environments [231]. The cocoon overpressure causes the formation of a series of oblique shocks within the beam in which the synchrotron emission is enhanced. In long term simulations (Figure 17), the evolution is dominated by a strong deceleration phase during which large lobes of jet material (like the ones observed in many FR IIs, e.g., Cyg A [43]) start to inflate around the jet’s head. These simulations reproduce some properties observed in powerful extragalactic radio jets (lobe inflation, hot spot advance speeds and pressures, deceleration of the beam flow along the jet) and can help to constrain the values of basic parameters (such as the particle density and the flow speed) in the jets of real sources.

Figure 17

Logarithm of the proper rest mass density and energy density (from top to bottom of an evolved, powerful jet propagating through the intergalactic medium. The white contour encompasses the jet material responsible for the synchrotron emission.

The problem of jet composition remains open for more than two decades. Measurements of circular polarization in jets [126] favour e^-/e⁺ jets. However, X-ray observations of blazars associated with OVV quasars impose strong constraints on the e^-/e⁺ pair content of jets [262]. On the other hand, the composition of jets is tightly related to their formation mechanisms [48, 266] and can be on the basis of the FR I/FR II dichotomy [47]. In Scheck et al. [255] the problem of the jet composition (e/p versus e^-/e⁺) has been approached in the context of long-term relativistic simulations (≈ 6 × 10⁶ yr) searching for signatures of the composition in the extended morphology of radio jets. Both the morphology and the dynamic behaviour are almost independent of the composition assumed for the jets in their 2D simulations (see Figure 18 and the MPEG movie in Figure 19).

Figure 18

Snapshots of the logarithm of the density (normalized to the density of the ambient medium for a cold baryonic (top panel, a cold leptonic (central panel and a hot leptonic (bottom panel relativistic jet at t ≈ 6.3 · 10⁶ y, respectively (from Scheck et al. [255]). The black lines are iso-contours of the beam mass fraction with X = 0.1 (outermost) and X = 0.9 (innermost). These values correspond to the boundaries of the cocoon and the beam, respectively. The time evolution of the hot leptonic model is shown in the MPEG movie in Figure 19.

Figure 19

mpg-Movie (11.8 MB) Still from a MPEG movie showing the logarithm of the density (normalized to the density of the ambient medium for a hot leptonic relativistic jet at t ≈ 6.3 · 10⁶y (from Scheck et al. [255]). >(For video see appendix)

The development of multi-dimensional relativistic hydrodynamic codes has allowed, for the first time, the simulation of parsec scale jets and superluminal radio components [110, 106, 147, 194]. The presence of emitting flows at almost the speed of light enhances the importance of relativistic effects in the appearance of these sources (relativistic Doppler boosting, light aberration, time delays). Hence, one should use models which combine hydrodynamics and synchrotron radiation transfer when comparing with observations. In these models, moving radio components are obtained from perturbations in steady relativistic jets. Where pressure mismatches exist between the jet and the surrounding atmosphere, reconfinement shocks are produced. The energy density enhancement produced downstream from these shocks can give rise to stationary radio knots as observed in many VLBI sources. Superluminal components are produced by triggering small perturbations in these steady jets which propagate at almost the jet flow speed. One example of this is shown in Figure 20 (see also [110, 106]), where a superluminal component (apparent speed ≈ 7 times the speed of light) is produced from a small variation of the beam flow Lorentz factor at the jet inlet. The dynamic interaction between the induced traveling shocks and the underlying steady jet can account for the complex behavior observed in many sources [109].

Figure 20

Computed radio maps of a compact relativistic jet showing the evolution of a superluminal component (from left to right. Two resolutions are shown: present VLBI resolution (white contours and resolution provided by the simulation (black/white images.

The linear stability analysis of relativistic flows against Kelvin-Helmholtz perturbations goes back to the seventies (see [23] for a review). Nowadays, the combination of hydrodynamical simulations and linear stability analysis has provided another step towards the comprehension of relativistic jets in extragalactic sources and micro-quasars. It is widely accepted that most of the features (even the large amplitude ones) observed in real jets admit an interpretation in terms of the growth of Kelvin-Helmholtz normal modes. This linear stability analysis has been succesfully applied to probe the physical conditions in the jets of several sources (e.g., S5 0836+710 [165], 3C273 [166], 3C120 [294]; see also the introduction of [118]). In [119, 251], the internal structures found in a set of relativistic axisymmetric kiloparsec jet simulations were analyzed. In the context of steady, parsec scale jets, a combination of linear stability analysis and axisymmetric hydrodynamical simulations has been used to predict the existence of fine structure appearing in the wake of superluminal components [3], later discovered in 3C120 [107]. Finally, in [117, 118] the analysis is extended to the three-dimensional structures generated in steady jets by precession and focussing on the distributions of internal energy density and flow velocity.

Magneto-hydrodynamic simulations of relativistic jets have been performed in 2D [138, 136] and 3D [209, 210] to study the implications of ambient magnetic fields in the morphology and bending properties of relativistic jets. However, despite the impact of these results on specific problems like, e.g., the understanding of the misalignment of jets between parsec and kiloparsec scales, these 3D simulations have not addressed the effects on the jet structure and dynamics of the third spatial degree of freedom. This has been the aim of the work of Aloy et al. [5] and Hughes et al. [128]. The latter authors have also used their three-dimensional code to study the deflection and precession of relativistic flows when impinging on an oblique density gradient.

Finally, Koide et al. [140, 141] have developed a general relativistic MHD code and applied it to the problem of jet formation from (Schwarzschild and Kerr) black hole accretion disks in the context of Blandford and Payne’s mechanism [27]. In the case of jets from Schwarzschild black holes [139], jets are formed with a two-layered shell structure consisting of a fast gas pressure driven jet (Lorentz factor ≈ 2) in the inner part and a slow magnetically driven outflow in the outer part, both of which are being collimated by the global poloidal magnetic field penetrating the disk. In the case of counter-rotating disks around Kerr black holes [137], a new powerful magnetically driven jet is formed inside the gas pressure driven jet. This jet is accelerated by a strong magnetic field created by frame dragging in the black hole ergosphere. Through this process, the magnetic field extracts the energy from the black hole corroborating Blandford and Znajek’s mechanism [28]. The same authors [142] have further explored this second mechanism for jet formation in the case of a Kerr black hole at maximal rotation immersed in a uniform, magnetically dominated corona with no disk. The magnetic field lines across the ergosphere are twisted by frame dragging. The line twist propagates outwards as a torsional Alfven wave train carrying electromagnetic energy and leading to the generation of a Poynting flux jet. Using a 3D GRMHD code, Nishikawa et al. [211] have investigated the dynamics of a freely falling corona and of a Keplerian accretion disk around a Schwarzschild black hole. The disk and the corona are threaded by a uniform poloidal magnetic field. The magnetic field is tightly twisted by the rotation of the disk, and plasma in the corona is accelerated by the Lorentz force to form bipolar relativistic jets as in previous simulations assuming axisymmetry.

Finally, let us note that direct numerical simulations of the Blandford and Znajek mechanism have been undertaken by Komissarov [145], solving the time dependent equations of (force-free, de generate) electrodynamics in a Kerr black hole magnetosphere. The equations are hyperbolic [146] and are solved by means of a Godunov type method.

7.2 Gamma-ray bursts (GRBs)

A second phenomenon which involves flows with velocities very close to the speed of light are gamma-ray bursts (GRBs). Although known observationally since over 30 years, their nature is still a matter of controversial debate. GRBs do not repeat except for a few soft gamma-ray repeaters. They are detected with a rate of about one event per day, and their duration varies from milliseconds to minutes. The duration of the shorter bursts and the temporal substructure of the longer bursts imply a geometrically small source (less than ∼ c · 1 msec ∼ 100 km), which in turn points towards compact objects like neutron stars or black holes. The emitted gamma-rays have energies in the range 30 keV to 2 MeV, the spectra being non-thermal (for recent reviews see, e.g., [45, 73, 192, 224, 225, 226].

Concerning the distance of GRB sources, major progress has first occurred through the observations by the BATSE detector on board the Compton Gamma-Ray Observatory (GRO), which have proven that GRBs are distributed isotropically over the sky [188]. However, until 1997 no counterparts (quiescent as well as transient) could be found, and observations did not provide a direct measurement of their distance. Then, in 1997, the detection and the rapid availability of accurate coordinates (∼ arcminutes) of the fading X-ray counterparts of GRBs by the Italian-Dutch BeppoSAX spacecraft [61, 228] has allowed for subsequent successful ground based observations of faint GRB afterglows at optical [283], millimeter [36], and radio [94] wavelengths (for a review see, e.g., [284]). In case of GRB 990123, the optical, X-ray, and gamma-ray emission was detected for the first time almost simultaneously (optical observations began 22 seconds after the onset of the GRB) [39, 4]. Updated information on GRBs which have been localized within a few hours to days to less than 1 degree by various instruments and procedures can be obtained from a web site maintained by Greiner [116].

As of June 2002, the distances of about two dozen gamma-ray bursts have been determined from optical spectra of the GRB afterglows and/or of the GRB host galaxies (for an overview see [116]). The observed redshifts confirm that (probably most) GRBs occur at cosmological distances.

Assuming isotropic emission, the inferred total energy of cosmological GRBs emitted in form of gamma-rays ranges from 5 × 10⁵¹ erg to about 10⁵⁴ erg, the record presently being held by GRB 990123 with 1.44 × 10⁵⁴ erg [29, 95]. The median bolometric isotropic equivalent prompt energy release is 2.2 × 10⁵³ erg, with an rms scatter of 0.80 dex [29].

In April 1998, the pure cosmological origin of GRBs was challenged by the detection of the Type Ib/c supernova SN 1998bw [98, 99] within the 8 arcminute error box of GRB 980425 [263, 222]. Its explosion time is consistent with that of the GRB, and relativistic expansion velocities are derived from radio observations of SN 1998bw [149]. BeppoSAX detected two fading X-ray sources within the error box, one being positionally consistent with the supernova and a fainter one not consistent with the position of SN 1998bw [222]. As the host galaxy ESO 184-82 of SN 1998bw is only at a redshift of z = 0.0085 [278], it was not difficult to study and analyze this particular GRB/supernova.

Assuming isotropic emission the total energy radiated by GRB 980425 in form of gamma-rays is only 7 × 10⁴⁷ erg [44], i.e., more than four orders of magnitude smaller than that of a typical cosmological GRB. The optical spectra and light curve of the associated supernova SN 1998bw can be modelled very well by an unusually energetic explosion (kinetic energy of the ejectg (2–5) × 10⁵² erg) of a massive star composed mainly of carbon and oxygen, i.e., by a very energetic SNe Ib/c [99, 131, 302]. Thus, Iwamoto et al. [131] called SN 1998bw a hypernova, a name which was originally proposed by Paczyński [217] for very luminous GRB/afterglow events.

As of June 2002, besides SN 1998bw/GRB 980425 two other SN-GRB associations have been discovered: SN 1997cy/GRB 970514 [101, 281] and SN 2001ke/GRB 011121 [100, 31, 237]. In addition, several other hypernovae have been observed (see, e.g., [186, 185]) where no associated GRB has been detected, while several other GRBs show indirect evidence for an association with a supernova like, e.g., a deviation from a power-law decline of the afterglow light curve (see e.g., [30]) or the presence of metal-enriched circumburst matter at high velocity (∼ 0.1c) [239]. Hence, observational data show evidence for an association (of at least a sub-class) of GRBs with type Ib/Ic core collapse supernovae resulting from the death of a massive star with a rich circumburst medium fed by the mass-loss wind of the progenitor.

The redshift measurements of GRBs imply isotropic gamma-ray energy releases approaching ∼ 10⁵⁴ erg. To find an astrophysical site producing such a huge amount of gamma-ray energy within a few tenth of seconds or in an even shorter time poses a severe problem for any theoretical GRB model. However, this problem could be eased considerably, if the radiation from GRBs is strongly beamed. And indeed, there exists observational evidence that the gamma-ray and afterglow radiation of (some) GRBs is not emitted isotropically, but may be beamed (for a review see, e.g., [73]). In particular, the rapid temporal decay of several GRB afterglows is inconsistent with spherical (isotropic) blast wave models, and instead is more consistent with the evolution of a relativistic conical flow or jet after it slows down and spreads laterally [254].

Using all GRB afterglows with known distances (as of January 2001), Frail et al. [95] derived their conical opening angles. These show a wide variation (2° to 20°) reflecting the observed broad distribution in fluence and luminosity for GRBs. Taking the corrected emission geometry into ac count, Frail et al. find that the gamma-ray energy release is narrowly clustered around 5 × 10⁵⁰ erg, i.e., the central engines of GRBs release energies that are comparable to ordinary supernovae. A similar conclusion can be derived by estimating the fireball energy based on X-ray afterglow observations [96], and by modeling the broadband emission of well-observed afterglows [218].

The compact nature of the GRB source, the observed fluxes and the cosmological distance taken together imply a very large photon density in the gamma-ray emitting fireball, and hence a large optical depth for pair production. This is, however, inconsistent with the optically thin source indicated by the non-thermal gamma-ray spectrum, which extends well beyond the pair production threshold at 500 keV. This problem can be resolved by assuming an ultra-relativistic expansion of the emitting region, which eliminates the compactness constraint. The bulk Lorentz factors required are then W > 100 (for reviews see, e.g., [224, 226, 192]).

In order to explain the existence of highly relativistic outflow and the energies released in a GRB, various catastrophic collapse events have been proposed including neutron-star/neutron-star mergers [216, 111, 80], neutron-star/black-hole mergers [197], and collapsars and hypernovae [217, 301, 169, 170]. These models all rely on a common engine, namely a stellar mass black hole which accretes several solar masses of matter from a disk (formed during a merger or by a nonspherical core collapse) at a rate of ∼ 1 M_⊙ s⁻¹ [235]. A fraction of the gravitational binding energy released by accretion is converted into neutrino and anti-neutrino pairs, which in turn annihilate into electron-positron pairs. This creates a pair fireball, which will also include baryons present in the environment surrounding the black hole. Provided the baryon load of the fireball is not too large, the baryons are accelerated together with the e^-/e⁺ pairs to ultra-relativistic speeds with Lorentz factors > 10² [46, 227, 224] .

Current observational facts and theoretical considerations suggest that GRBs involve three evolutionary stages (for reviews see e.g., [225, 192]):

• A compact source, which is opaque to gamma-rays and which cannot be observed directly, produces a relativistic energy flow.

• The energy is transfered by means of a highly irregular flow of relativistic particles (or less likely by Poynting flux) from the compact source to distances larger than ∼ 10¹³ cm where the flow becomes optically thin.

• The relativistic flow is slowed down and its bulk kinetic energy is converted into internal energy of accelerated non-thermal particles, which in turn emit the observed gamma-rays via cyclotron radiation and/or inverse Compton processes. The dissipation of kinetic energy either occurs through external shocks arising due to the interaction of the flow with circumburst matter, or through internal shocks arising when faster shells overtake slower ones inside the irregular outflow (internal-external shock scenario).

One-dimensional numerical simulations of spherically symmetric relativistic fireballs from GRB sources have been performed by several authors [227, 219, 135, 66, 273]. Panaitescu et al. [219] modelled the interaction between an expanding adiabatic fireball and a stationary external medium whose density is either homogeneous or varies with distance according to a power law. They used a hybrid code based on standard Eulerian finite difference techniques in most of the computational domain and a Glimm algorithm including an exact Riemann solver in regions where discontinuities are present [295]. They simulated the evolution until most of the fireball’s kinetic energy was converted into internal energy. Kobayashi et al. [135] studied the evolution of an adiabatic relativistic fireball expanding into a cold uniform medium using a relativistic Lagrangian code based on a second-order Godunov method with an exact Riemann solver. They simulated the initial free expansion and acceleration of the fireball, its coasting, and deceleration to non-relativistic velocities. Daigne and Mochkovitch [66] used a Lagrangian hydrodynamics code based on relativistic PPM [60, 181] (extended by them to spherical symmetry) to simulate the evolution of internal shocks in a relativistic wind with a very inhomogeneous initial distribution of the Lorentz factor. Tan et al. [273] investigated the acceleration of shock waves to relativistic velocities in the outer layers of exploding stars. By concentrating the energy of the explosion in the outermost ejecta, such trans-relativistic blast waves can serve as the progenitors of GRBs. For their study they developed a relativistic 1D Lagrangian hydrodynamics code based on an exact Riemann solver [181].

Multi-dimensional modeling of ultra-relativistic jets in the context of GRBs has for the first time been attempted by Aloy et al. [7]. Using a collapsar progenitor model of MacFadyen and Woosley [169], they simulated the propagation of an axisymmetric jet through the mantle and envelope of a collapsing massive star (10 M_⊙,) using the GENESIS special relativistic hydrodynamics code [6]. The jet forms as a consequence of an assumed energy deposition of 10⁵¹ erg s⁻¹ within a 30 degree cone around the rotation axis. At breakout, i.e., when the jets reach the surface of the stellar progenitor, the maximum Lorentz factor of the jet flow is about 20. The latter fact implies that Newtonian simulations of this phenomenon [169] are inadequate. An MPEG movie (Figure 21) shows the evolution of the Lorentz factor while the jet is propagating through the collapsar progenitor.

Figure 21

mpg-Movie (14.2 MB) Still from a MPEG movie illustrating the propagation of a relativistic jet from a collapsar, whose progenitor is a rotating He star with a radius of 3 × 10¹⁰ cm. All three panels show the rest mass density distribution. The left panel displays the computational domain up to the head of the jet (note the changing axis and color scales. The upper right panel shows the central region (scale fixed where the jet forms due to a prescribed time-independent and spatially localized energy deposition rate (10⁵⁰ erg s⁻¹). One can recognize the central spherical region (black circle of radius 2 × 10⁷ cm which was excised from the computational domain. It contains a (rotating) black hole of initially three solar masses accreting matter through the inner grid boundary. The lower right panel provides a global view (scale fixed of the computational domain up to the surface of the He star progenitor. (Movie courtesy of M.A. Aloy.) (For video see appendix)

Zhang, Woosley, and MacFadyen [308] performed a parameter study of the propagation of 2D relativistic jets through the stellar progenitor of a collapsar by varying the initial Lorentz factor, opening angle, power, and internal energy of the jet as well as the radius where it is introduced. They find, in agreement with Aloy et al. [7], that relativistic jets are collimated by their passage through the stellar mantle, and that the jet has a moderate Lorentz factor and very large internal energy when it emerges from the star. Zhang et al. [308] also simulated the evolution after the escape of the jet. During this phase, conversion of the internal energy leads to a further acceleration of the jet, thereby boosting its Lorentz factor to a terminal value of approximately 150 for the initial conditions chosen.

Granot et al. [114, 115] performed 2D and 3D relativistic hydrodynamic simulations of the deceleration and lateral expansion of an adiabatic relativistic jet with an initial Lorentz factor of 23.7 as it expands into an ambient medium. The hydrodynamic calculations used an adaptive mesh refinement (AMR) code. They found that the sideways propagation is different than predicted by simple analytic models. The physical conditions at the sides of the jet are significantly different from those at the front of the jet, and most of the emission occurs within the initial opening angle of the jet assumed to be 0.2 radians.

7.3 Relativistic heavy ion collisions (RHIC)

Special relativistic “flows” are also encountered in heavy ion collision experiments where heavy ions (of mass number A) are accelerated up to ultra-relativistic velocities and collided with one another. Heavy ion collisions are the only means to compress and heat up nuclear matter in the laboratory, and to prove the existence of the quark-gluon plasma predicted by quantum chromodynamics [56, 63]. They also provide a terrestrial possibility to test the solutions of relativistic fluid dynamics, and to gain important information relevant for different areas of astrophysics like, e.g., the early universe, neutron stars, and supernova explosions. A discussion of the experimental and theoretical methods and results of RHIC is far beyond the scope of this review. Thus, we will address here only some issues related to numerical simulations of RHIC by means of relativistic hydrodynamics.

The compressibility and other basic properties of the nuclear equation of state, phase transitions in nuclear matter, and nuclear interactions can be studied in relativistic heavy ion reactions at beam energies in the range of 100A MeV to 10A GeV. In order to search for the existence of the quark-gluon plasma, ultra-relativistic heavy ion collision experiments with beam energies exceeding l0AGeV must be performed [56]. Up to low ultra-relativistic energies baryons stemming from the projectile and the target are fully or partly stopped by each other forming a baryon rich matter in the center of the reaction zone. This regime is called the stopping energy region. At even larger energies the theorectical expectation is that the (initial) baryon charge of the target and projectile is so far apart in phase space that it cannot be slowed down completely during the heavy ion collision. In this so-called transparent energy regime the quanta carrying the baryon charge will essentially keep their initial velocities, i.e., the center of the reaction zone will be almost baryon free. However, much energy will be deposited in this baryon free region, and the resulting large energy density matter may form a quark-gluon plasma.

In order for a hydrodynamic description of heavy ion collisions to be applicable, several criteria must be fulfilled [56]:

• many degrees of freedom in the system,

• a short mean free path,

• short mean stopping length,

• sufficient reaction time for thermal equilibrium, and

• a short de Broglie wavelength.

The first condition is satisfied reasonably well when there are many nucleons involved in the collision and when pion production or resonance excitations become important, i.e., for almost central collisions of sufficiently heavy and energetic ions. The mean free path of a nucleon in nuclear matter scales inversely with the nucleon-nucleon cross section, and is about ∼ 0.3 fm at a bombarding energy of 200 MeV, which is short compared to the radii of heavy nuclei. However, the mean free path increases with energy. The average distance it takes for a nucleon in nuclear matter to dissipate its kinetic energy is called the mean stopping length. At 200 MeV a nucleon will penetrate about 2 fm into a nucleus. But at larger energies the mean stopping length may exceed the nuclear radius (there exist effects both increasing and decreasing the mean stopping length [56]), i.e., the colliding nuclei will appear partially or nearly transparent to one another. Modifications to the hydrodynamic equations are then necessary. The establishment of local thermal equilibrium seems to be reasonably well satisfied in heavy ion collisions. Finally, at bombarding energies of interest the de Broglie wavelength is about 2 fm or smaller, which is small compared to the nuclear radius.

Hydrodynamic simulations of heavy ion collisions are complicated by additional physical and numerical issues [56, 63]. We will mention only a few of these issues here.

Since ideal hydrodynamics assumes that matter is in local thermal equilibrium at every instant, colliding fluid elements are forced by momentum conservation to instantaneously stop and by energy conservation to convert all their kinetic energy into thermal energy. Thus, when immediate complete stopping is not achieved at large beam energies, non-ideal hydrodynamics must be considered (see, e.g., Elze et al. [82]). However, the viability of non-ideal hydrodynamics as a causal theory is still a matter of debate, and there are still open questions concerning the proper relativistic generalization [56, 125]. In the ultra-relativistic regime, where the stopping power becomes very low, matter in the high energy density, baryon-free central region is supposed to establish local thermal equilibrium within a (proper) time of order 1 fm/c, i.e., the subsequent evolution can be described by ideal hydrodynamics.

Numerical algorithms for RHIC must scope with the presence of (almost) vacuum in the baryon-free central region. This can cause problems due to erroneous (i.e., numerical) acausal transport of matter [244]. Another challenge is posed by the phase transition to the quark-gluon plasma, which is usually assumed to be of first order. Matter undergoing a first-order phase transition may exhibit thermodynamically anomalous behaviour (changes in the convexity of isentropes) which can cause important consequences for the wave structure of the hydrodynamic equations leading to non-uniqueness of solutions of Riemann problems (see Section 9.1).

The performance of numerical algorithms for RHIC (RHLLE and FCT SHASTA) in the presence of vacuum and for thermodynamically anomalous matter were systematically explored by Rischke et al. [244, 246].

8 Conclusion

8.1 Evaluation of the methods

An assessment of the quality of a numerical method for special relativistic flow should consider, at least, the following aspects:

• the accuracy and robustness in describing high Lorentz factor flows with strong shocks,

• the effort required to extend to multi-dimensions, and

• the effort required to extend to RMHD and GRHD.

These aspects are summarized in Table 12 for most of the numerical methods discussed in this review.

Table 12 Evaluation of numerical methods for SRHD. Methods have been categorized for clarity.

Since their introduction in numerical RHD in the early 1990s, Riemann-solver-based HRSC methods have demonstrated their ability to describe accurately (i.e., in a stable way and without excessive smearing) relativistic flows of arbitrarily large Lorentz factors and strong discontinuities reaching the same quality as in classical hydrodynamics. In addition (as it is the case for classical flows, too), HRSC methods show the best performance compared to any other method (e.g., artificial viscosity, FCT or SPH). This last assertion applies also to the symmetric HRSC relativistic algorithms developed recently.

Nevertheless, a lot of effort has been put into improving non-HRSC methods. Using a consistent formulation of artificial viscosity has significantly enhanced the capability of SPH (e.g., [261]) and of finite difference schemes. A good example of the latter case is the algorithm recently proposed in [10], but the 40% overshoot in the post-shock density in Problem 2 confirms the need for an implicit treatment of the equations as originally proposed by [213]. Concerning relativistic SPH, recent investigations using a conservative formulation of the hydrodynamic equations [53, 261, 204] have reached an unprecedented accuracy compared to previous SPH simulations, although some issues still remain. Besides the strong smearing of shocks, the description of contact discontinuities and of thin structures moving at ultra-relativistic speeds needs to be improved (see Section 6.2).

Concerning FCT, codes based on a conservative formulation of the RHD equations have been able to handle special relativistic flows with discontinuities at all flow speeds, although the quality of the results is lower than that of HRSC methods in all cases [256, 244, 246].

The extension to multi-dimensions is straightforward for most relativistic codes. Finite difference techniques are easily extended using directional splitting. HRSC methods based on exact solutions of the Riemann problem [181, 295] benefit from the development of a multi-dimensional relativistic Riemann solver [234]. The adaptive grid, artificial viscosity, implicit code of Norman and Winkler [213], and the relativistic Glimm method of Wen et al. [295] are restricted to one-dimensional flows. The latter method produces the best results in all the tests analyzed in Section 6.

The symmetric TVD scheme proposed by Davis [68] and extended to GRMHD (see below) by Koide et al. [138] combines several characteristics making it very attractive. It is written in conservation form and is TVD, i.e., it is converging to the physical solution. In addition, it does not require spectral information, and hence allows for a simple extension to RMHD. Quite similar statements can be made about the approach proposed by van Putten [287]. In contrast to FCT schemes (which are also easily extended to general systems of equations), both Koide et al.’s and van Putten’s methods are very stable when simulating mildly relativistic flows (maximum Lorentz factors ≈ 4) with discontinuities. Their only drawback is an excessive smearing of the latter. Expectations concerning the correct description of ultrarelativistic MHD flows by means of symmetric TVD schemes may be met in the near future by global third-order symmetric schemes [72].

Concerning the extension of Riemann-solver-based HRSC schemes to RMHD, we mention the efforts by Balsara [14] and Komissarov [143] in 1D and 2D RMHD (see Section 8.2.4).

8.2 Present and future developments

The directions of present and future developments in RHD are quite obvious, and can be divided into four main categories:

8.2.1 Incorporation of realistic microphysics

Up to now most astrophysical SRHD simulations have assumed matter whose thermodynamic properties can be described by an inviscid ideal equation of state with a constant adiabatic index. This simplification may have been appropriate in the first generation of SRHD simulations, but it clearly must be given up when aiming at a more realistic modeling of astrophysical jets, gamma-ray burst sources, or accretion flows onto compact objects. For these phenomena a realistic equation of state should include contributions from radiation (γ = 4/3 “fluid”), allow for the formation of electron-positron pairs at high temperatures, and allow the ideal gas contributions to be arbitrarily degenerate and/or relativistic.

Depending on the problem to be simulated, effects due to heat conduction, diffusion, radiation transport, cooling, nuclear reactions, and viscosity may have to be considered, too. Including any of these effects is often a non-trivial task even in Newtonian hydrodynamics, as the differential operators describing advection and convection are of hyperbolic nature, while diffusion and conduction processes give rise to parabolic differential operators, and the treatment of constraints or self-gravity involves differential operators of elliptic type (see, e.g., the contributions in the book edited by Steiner and Gautschy [268]). There has been considerable development in the coupling of Newtonian HRSC methods to the nonhyperbolic terms arising in the equations from these physical processes using semi-implicit approaches, e.g., the predictor-corrector method [18]. Another example in this context provides the recent work of Howell and Grenough [127], who have coupled an explicit Newtonian Godunov-type integrator for the hyperbolic hydrodynamic equations to an implicit multigrid solver to describe effects of radiative diffusion on the flow and vice versa. We particularly mention this work here, as it also uses a block-structured adaptive mesh refinement algorithm (see Section 8.2.2). Although such sophisticated methods have not been applied in SRHD yet, they represent an important set of ideas that could provide a starting point for more elaborate SRHD simulations.

In the context of relativistic jets, Komissarov and Falle [148], and Scheck et al. [255] have considered a mixture of ideal, relativistic Boltzmann gases [272] hence allowing for jets with general (i.e., e, e⁺, p) composition. The usage of such a more general ideal EOS causes no special problem for the Riemann solvers although a higher nonlinearity is introduced in the process of the recovery of the primitive variables. In order to avoid this extra complexity, approximate expressions for the relativistic ideal gas EOS have been proposed [79, 265]. In case of the approximation proposed by Sokolov et al. [265], the recovery of the primitive variables is explicit. Moreover, the authors have developed an exact Riemann solver consistent with the approximate EOS.

An EOS describing matter consisting of a set of ideal, non-relativistic Boltzmann gases (nuclei in nuclear statistical equilibrium), a Fermi gas of electrons and photons was used in the simulations of relativistic jets from collapsars by Aloy et al. [7].

HRSC flow simulations involving elaborate microphysics may require the extension of the presently available relativistic Riemann solvers to handle general equations of state (see Section 9.1). This is the case for the Roe-Eulderink method, which can be extended following the procedure developed in the classical case by Glaister [103]. Methods based on exact solutions of the Riemann problem, like rPPM and rGlimm, can take advantage of the solution presented in Section 2.3 to cope with a general EOS. FCT based difference schemes used in simulations of relativistic heavy ion collisions (see Section 7.3) pose no specific numerical problem in handling a general EOS.

Another interesting area that deserves further research is the application of relativistic HRSC methods in simulations of reactive multi-species flows, especially as such flows still cause problems for the Newtonian CFD community (see, e.g., [232]). The structure of the solution to the Riemann problem becomes significantly more complex with the introduction of reactions between multiple species. Riemann solvers that incorporate source terms [160], and in particular source terms due to reactions, have been proposed for classical flows [19, 132]. However, most HRSC codes still rely on operator splitting.

Peitz and Appl [221] have addressed the difficult issue of non-ideal GRHD, which is of particular importance, e.g., for the simulation of accretion discs around compact objects, rotating relativistic fluid configurations, and the evolution of density fluctuations in the early universe. They have accounted for dissipative effects by applying the theory of extended causal thermodynamics, which eliminates the causality violating infinite signal speeds arising from the conventional Navier-Stokes equation. However, Peitz, and Appl have not yet implemented their model numerically.

A description of non-ideal hydrodynamics in general relativity is also the aim of Richardson and Chung’s work [242], although from a less formal basis. The authors introduce an approach (the so-called flow-field-dependent variation theory [54, 55] resting on the conservative Navier-Stokes system of equations for classical fluid dynamics) where local properties of the flow (advection, turbulence, or gravity dominated) are captured in terms of relevant parameters (measuring changes of the Lorentz factor, relativistic Reynolds and Fronde numbers between adjacent numerical zones, respectively). These parameters are then used to produce a suitable numerical model (hyperbolic, parabolic, elliptic) which is subsequently discretized using finite difference or finite element methods. The latter approach has been applied by Richardson and Chung [242] for several test cases (mildly relativistic Riemann problem and general relativistic spherical dust infall).

8.2.2 Coupling of SRHD schemes with AMR

Modeling astrophysical phenomena often involves an enormous range of length and time scales to be covered in the simulations (see, e.g., [205]). In two and definitely in three spatial dimensions many such simulations cannot be performed with sufficient spatial resolution on a static equidistant or non-equidistant computational grid, but they rather require dynamic, adaptive grids. In addition, when the flow problem involves stiff source terms (e.g., energy generation by nuclear reactions), very restrictive time step limitations may result. A promising approach to overcome these complications is the coupling of SRHD solvers with the adaptive mesh refinement (AMR) technique [21]. AMR automatically increases the grid resolution near flow discontinuities or in regions of large gradients (of the flow variables) by introducing a dynamic hierarchy of grids until a prescribed accuracy of the difference approximation is achieved. Because each level of grids is evolved in AMR on its own time step, time step restrictions due to stiff source terms constrain the computational costs less than without AMR.

For an overview of online information about AMR visit, e.g., the AMRA home page of Plewa [229], and for public domain AMR software, e.g., the AMRCLAW home page of LeVeque and Berger [162], the web page of the Lawrence Berkeley Lab dedicated to AMR [1], and the NASA Goddard Space Flight Center web page on PARAMESH [171]. Astrophysical applications based on PARAMESH can be found at the web site of the ASCI / Alliances Center for Astrophysical Thermonuclear Flashes at the University of Chicago [2]. Although, as demonstrated by these web sites, there has been a considerable effort over the last few years in developing frameworks for block-structured adaptive mesh refinement, we will see that the application to SRHD is still in its infancy.

An SRHD simulation of a relativistic jet based on a combined HLL-AMR scheme was performed by Duncan and Hughes [78]. Plewa et al. [231, 230] have modeled the deflection of highly supersonic slab jets propagating through non-homogeneous environments using the HRSC scheme of Martí et al. [183] combined with the AMR implementation AMRA of Plewa [229]. A similar study, but in 3D, was performed by Hughes et al. [128] who studied the deflection and precession of cylindrical relativistic jets when impinging on an oblique density gradient using the SRHD code of Duncan and Hughes [78] extended to 3D and their own implementation of the AMR technique of Berger and Colella [21]. Komissarov and Falle [147] have combined their numerical scheme with the adaptive grid code Cobra, which has been developed by Mantis Numerics Ltd. for industrial applications [88], and which uses a hierarchy of grids with a constant refinement factor of two between subsequent grid levels.

8.2.3 General relativistic hydrodynamics (GRHD)

Up to now only very few attempts have been made to extend HRSC methods to GRHD (for a comprehensive review see Font [91]). All these attempts are based on the usage of linearized Riemann solvers [179, 84, 249, 15, 93] . In the most recent of these approaches, Font et al. [93] have developed a 3D general relativistic HRSC hydrodynamic code where the matter equations are integrated in conservation form and fluxes are calculated with Marquina’s formula.

A very interesting and powerful procedure was proposed by Balsara [13] and has been implemented by Pons et al. [233]. This procedure allows one to exploit all the developments in the field of special relativistic Riemann solvers in general relativistic hydrodynamics. The procedure relies on a local change of coordinates at each zone interface such that the spacetime metric is locally flat. In that locally flat spacetime any special relativistic Riemann solver can be used to calculate the numerical fluxes, which are then transformed back. The transformation to an orthonormal basis is valid only at a single point in spacetime. Since the use of Riemann solvers requires the knowledge of the behavior of the characteristics over a finite volume, the use of the local Lorentz basis is only an approximation. The effects of this approximation will only become known through the study of the performance of these methods in situations where the structure of the spacetime varies rapidly in space and perhaps time as well. In such a situation finer grids and improved time advancing methods will definitely be required. The implementation is simple and computationally inexpensive.

Characteristic formulations of the Einstein field equations are able to handle the long term numerical description of single black hole spacetimes in vacuum [24]. In order to include matter in such an scenario, Papadopoulos and Font [220] have generalized the HRSC approach to cope with the hydrodynamic equations in such a null foliation of spacetime. Actually, they have presented a complete (covariant) reformulation of the equations in GR, which is also valid for spacelike foliations in SR. They have extensively tested their method, calculating, among other tests, shock tube problem 1 (see Section 6.2.1), but posed on a light cone and using the appropriate transformations of the exact solution [180] to account for advanced and retarded times.

Other developments in GRHD in the past included finite element methods for simulating spherically symmetric collapse in general relativity [173], general relativistic pseudo-spectral codes based on the (3+1) ADM formalism [11] for computing radial perturbations [112] and 3D gravitational collapse of neutron stars [32], general relativistic [172, 204] and post-Newtonian [12] SPH. The potential of these methods for the future is unclear, as none of them is specifically appropriate for ultra-relativistic speeds and strong shock waves which are characteristic of most astrophysical applications.

Let us remark that, in the case of dynamic spacetimes, the equations of relativistic hydrodynamics are solved on the local (in space and time) background solution provided by the Einstein equations at every time step [91]. The solution of the Einstein gravitational field equations and its coupling with the hydrodynamic equations is the realm of Numerical Relativity, which is beyond the scope of this article (see, e.g., Lehner [157] for a recent review).

8.2.4 Relativistic magneto-hydrodynamics (RMHD)

The inclusion of magnetic effects is of great importance for many astrophysical phenomena. The formation and collimation process of (relativistic) jets (powering powerful extragalactic radio sources, galactic microquasars, and GRBs) most likely involves dynamically important magnetic fields and occurs in strong gravitational fields. The same is likely to be true for accretion discs around black holes. Magneto-relativistic effects even play a non-negligible role in the formation of proto-stellar jets in regions close to the light cylinder [41]. Thus, relativistic MHD codes are a very desirable tool in astrophysics. The non-trivial task of developing such a kind of code is considerably simplified by the fact that because of the high conductivity of astrophysical plasmas one must only consider ideal RMHD in most applications.

The aim of any (Newtonian or relativistic) MHD code is to evolve the induction equation to obtain the magnetic fields from which to calculate the Lorentz force. Magnetic fields are divergence free, i.e., $\nabla \cdot \vec B = 0$. Hence, numerical schemes are required to maintain this constraint (if fulfilled for the initial data) during the evolution. A first step towards the development of a relativistic (in fact, general relativistic) MHD code was made by Evans and Hawley [86] who incorporated a numerical scheme for the induction equation (constrained transport), which maintained zero divergence of the magnetic field up to machine round-off error, into the axisymmetric, two-dimensional finite difference code of Hawley et al. [123]. In Evans and Hawley’s method the magnetic flux through cell interfaces is the fundamental "magnetic" variable. Their method is also based on the use of a staggered mesh (some quantities including the magnetic field components are defined at grid interfaces). Thus, even in classical MHD, the extension of the constrained transport method to Riemann-solver-based schemes (that rely on fluxes at cell interfaces derived from cell averaged quantities) is non-trivial [65, 252]. Tóth [280] reviews and compares strategies (namely the eight-wave formulation, several versions of the constrained transport, and the projection scheme) used in HRSC schemes in classical MHD to maintain the constraint $\nabla \cdot \vec B = 0$ numerically. His conclusions also apply to RMHD.

Special relativistic 2D MHD test problems with Lorentz factors up to ∼ 3 have been investigated by Dubal [77] with a code based on FCT techniques (see Section 4).

Van Putten [286, 287, 290] has proposed a method for accurate and stable numerical simulations of RMHD in the presence of dynamically significant magnetic fields in two dimensions and up to moderate Lorentz factors. The method is based on MHD in divergence form using a 2D shock-capturing method in terms of a pseudo-spectral smoothing operator (see Section 4). He applied the method to 2D blast waves [289] and astrophysical jets [288, 291].

In a series of papers, Koide and coworkers [138, 136, 209, 210, 139] have investigated relativistic magnetized jets using a symmetric TVD scheme (see Section 3). Koide, Nishikawa, and Mutel [138] simulated a 2D RMHD slab jet, whereas Koide [136] investigated the effect of an oblique magnetic field on the propagation of a relativistic slab jet. Nishikawa et al. [209, 210] extended these simulations to 3D and considered the propagation of a relativistic jet with a Lorentz factor W = 4.56 along an aligned and an oblique external magnetic field. The 2D and 3D simulations published up to now only cover the very early propagation of the jet (up to 20 jet radii) and are performed with moderate spatial resolution on an equidistant Cartesian grid (up to 101 zones per dimension, i.e., 5 zones per beam radius). Concerning higher order symmetric non-oscillatory schemes, the very recent work by Del Zanna et al. [72] has to be mentioned. Their third order scheme produces results which are competitive with those obtained by Riemann-solver based methods (see next paragraph) but avoiding all the complexity associated with the spectral decomposition into characteristic fields (particularly the degeneracies). Its high order and its simplicity make this approach very appealing.

Steps towards the extension of linearized Riemann solvers to ideal RMHD have already been taken. All theoretical aspects (RMHD as a quasi-linear hyperbolic system, spectral decomposition of the Jacobian of the flux vector in covariant form, study of simple waves and shock waves) are compiled in the book by Anile [8], augmenting previous work of Lichnerowicz [163]. Romero [250] derived an analytic expression for the spectral decomposition of the Jacobian matrix of the flux vector in the case of a planar relativistic flow field permeated by a transversal magnetic field (nonzero field component only orthogonal to flow direction). Anile and Pennisi [9] and Van Putten [292] studied the characteristic structure of the RMHD equations in (constraint free) covariant form. Finally, Balsara [14] and Komissarov [143] have developed robust, second-order accurate (in space and time), Godunov-type schemes for 1D and 2D RMHD, respectively. Both start from the spectral decomposition of the RMHD system of (ten) equations in covariant form, extract the relevant information (wave speeds, jumps in the characteristic variables) for the (seven) physical waves, and analyze the cases of degeneracy (i.e., cases where several wave speeds corresponding to different waves become degenerate). Komissarov’s RMHD scheme is an extension of the scheme developed for RHD [89] described in Section 3.5, which avoids the use of the left eigenvectors (in [14] they are computed numerically). In its multi-dimensional version, Komissarov’s code enforces $\nabla \cdot \vec B = 0$ by employing the integral form of the induction equation. This code has been used to study the propagation of light, highly relativistic jets carrying toroidal magnetic fields [144].

Koide, Shibata, and Kudoh [139] performed simulations of magnetically driven axisymmetric jets from black hole accretion disks. Their GRMHD code [140] is an extension of the special relativistic MHD code developed by Koide et al. [138, 136, 209]. The necessary modifications of the code were quite simple, because in the (nonrotating) black hole’s Schwarzschild spacetime the GRMHD equations are identical to the GRMHD equations in general coordinates, except for the gravitational force terms and the geometric factors of the lapse function. The authors have recently extended their code to Kerr spacetimes [141] and performed simulations of axisymmetric jets formed by extracting rotational energy from a black hole [137, 142]. Finally, using a 3D GRMHD code, Nishikawa et al. [211] have investigated the dynamics of a freely falling corona and of a Keplerian accretion disk around a Schwarzschild black hole to form bipolar relativistic jets assuming axisymmetry as in previous simulations.

With the pioneering work of Koide and collaborators, numerical simulations have entered into the realm of GRMHD. However, despite their success, present simulations only cover a tiny fraction of dynamical time scales (about 2 rotational periods of the accretion disk) and jets are formed with very small terminal speeds (Lorentz factors less than 2). Hence, the quest for robust codes able to follow the formation of steady relativistic jets is still open. Given their success in SRHD, the extension of Riemann-solver based HRSC methods is an obvious option to bear in mind. Again, the third-order symmetric HRSC algorithms developed recently [72] represent a very interesting alternative.