Spectral Methods for Numerical Relativity

Abstract

Equations arising in general relativity are usually too complicated to be solved analytically and one must rely on numerical methods to solve sets of coupled partial differential equations. Among the possible choices, this paper focuses on a class called spectral methods in which, typically, the various functions are expanded in sets of orthogonal polynomials or functions. First, a theoretical introduction of spectral expansion is given with a particular emphasis on the fast convergence of the spectral approximation. We then present different approaches to solving partial differential equations, first limiting ourselves to the one-dimensional case, with one or more domains. Generalization to more dimensions is then discussed. In particular, the case of time evolutions is carefully studied and the stability of such evolutions investigated. We then present results obtained by various groups in the field of general relativity by means of spectral methods. Work, which does not involve explicit time-evolutions, is discussed, going from rapidly-rotating strange stars to the computation of black-hole-binary initial data. Finally, the evolution of various systems of astrophysical interest are presented, from supernovae core collapse to black-hole-binary mergers.

1 Introduction

Einstein’s equations represent a complicated set of nonlinear partial differential equations for which some exact [30] or approximate [31] analytical solutions are known. But these solutions are not always suitable for physically or astrophysically interesting systems, which require an accurate description of their relativistic gravitational field without any assumption on the symmetry or with the presence of matter fields, for instance. Therefore, many efforts have been undertaken to solve Einstein’s equations with the help of computers in order to model relativistic astrophysical objects. Within this field of numerical relativity, several numerical methods have been experimented with and a large variety are currently being used. Among them, spectral methods are now increasingly popular and the goal of this review is to give an overview (at the moment it is written or updated) of the methods themselves, the groups using them and the results obtained. Although some of the theoretical framework of spectral methods is given in Sections 2 to 4, more details can be found in the books by Gottlieb and Orszag [94], Canuto et al. [56, 57, 58], Fornberg [79], Boyd [48] and Hesthaven et al. [117]. While these references have, of course, been used for writing this review, they may also help the interested reader to get a deeper understanding of the subject. This review is organized as follows: hereafter in the introduction, we briefly introduce spectral methods, their usage in computational physics and give a simple example. Section 2 gives important notions concerning polynomial interpolation and the solution of ordinary differential equations (ODE) with spectral methods. Multidomain approach is also introduced there, whereas some multidimensional techniques are described in Section 3. The cases of time-dependent partial differential equations (PDE) are treated in Section 4. The last two sections then review results obtained using spectral methods: for stationary configurations and initial data (Section 5), and for the time evolution (Section 6) of stars, gravitational waves and black holes.

1.1 About spectral methods

When doing simulations and solving PDEs, one faces the problem of representing and deriving functions on a computer, which deals only with (finite) integers. Let us take a simple example of a function f: [−1, 1] → ℝ. The most straightforward way to approximate its derivative is through finite-difference methods: first one must setup a grid

$${\{{x_i}\} _{i = 0 \ldots N}} \subset [ - 1,1]$$

of N + 1 points in the interval, and represent f by its N + 1 values on these grid points

$${\{{f_i} = f({x_i})\} _{i = 0 \ldots N}}.$$

then, the (approximate) representation of the derivative f′ shall be, for instance,

$$\forall i < N,f_i^\prime = f^{\prime}({x_i}) \simeq {{{f_{i + 1}} - {f_i}} \over {{x_{i + 1}} - {x_i}}}.$$

(1)

If we suppose an equidistant grid, so that ∀i < N, x_i+1 − x_i = Δx = 1/N, the error in the approximation (1) will decay as Δx (first-order scheme). One can imagine higher-order schemes, with more points involved for the computation of each derivative and, for a scheme of order n, the accuracy can vary as (Δx)ⁿ = 1/Nⁿ.

Spectral methods represent an alternate way: the function f is no longer represented through its values on a finite number of grid points, but using its coefficients (coordinates) {c_i}_i=0…N in a finite basis of known functions {Φ_i}_i=0…N

$$f(x) \simeq \sum\limits_{i = 0}^N {{c_i}{\Phi _i}(x)}.$$

(2)

A relatively simple case is, for instance, when f(x) is a periodic function of period two, and the Φ_2i(x) = cos(πix), Φ_2i+1(x) = sin(πix) are trigonometric functions. Equation (2) is then nothing but the truncated Fourier decomposition of f. In general, derivatives can be computed from the c_i’s, with the knowledge of the expression for each derivative Φ′_i(x) as a function of {Φ_i}_i=0…N. The decomposition (2) is approximate in the sense that {Φ_i}_i=0…N represent a complete basis of some finite-dimensional functional space, whereas f usually belongs to some other infinite-dimensional space. Moreover, the coefficients c_i are computed with finite accuracy. Among the major advantages of using spectral methods is the rapid decay of the error (faster than any power of 1/N, and in practice often exponential e^−N), for well-behaved functions (see Section 2.4.4); one, therefore, has an infinite-order scheme.

In a more formal and mathematical way, it is useful to work within the methods of weighted residuals (MWR, see also Section 2.5). Let us consider the PDE

$$Lu(x) = s(x)\quad x \in U \subset {{\mathbb R}^d},$$

(3)

$$Bu(x) = 0\quad x \in \partial U,$$

(4)

where L is a linear operator, B the operator defining the boundary conditions and s is a source term. A function ū is said to be a numerical solution of this PDE if it satisfies the boundary conditions (4) and makes “small” the residual

$$R = L\bar u - s.$$

(5)

If the solution is searched for in a finite-dimensional subspace of some given Hilbert space (any relevant $L_U^2$ space) in terms of the expansion (2), then the functions {Φ_i(x)}_i=0…N are called trial functions and, in addition, the choice of a set of test functions {ξ_i (x)}_i=0…N defines the notion of smallness for the residual by means of the Hilbert space scalar product

$$\forall i = 0 \ldots N,\quad ({\xi _i},R) = 0{.}$$

(6)

Within this framework, various numerical methods can be classified according to the choice of the trial functions:

• Finite differences: the trial functions are overlapping local polynomials of fixed order (lower than N).

• Finite elements: the trial functions are local smooth functions, which are nonzero, only on subdomains of U.

• Spectral methods: the trial functions are global smooth functions on U.

Various choices of the test functions define different types of spectral methods, as detailed in Section 2.5. Usual choices for the trial functions are (truncated) Fourier series, spherical harmonics or orthogonal families of polynomials.

1.2 Spectral methods in physics

We do not give here all the fields of physics in which spectral methods are employed, but sketching the variety of equations and physical models that have been simulated with such techniques. Spectral methods originally appeared in numerical fluid dynamics, where large spectral hydro-dynamic codes have been regularly used to study turbulence and transition to the turbulence since the seventies. For fully resolved, direct numerical calculations of Navier-Stokes equations, spectral methods were often preferred for their high accuracy. Historically, they also allowed for two or three-dimensional simulations of fluid flows, because of their reasonable computer memory requirements. Many applications of spectral methods in fluid dynamics have been discussed by Canuto et al. [56, 58], and the techniques developed in that field are of some interest to numerical relativity.

From pure fluid-dynamics simulations, spectral methods have rapidly been used in connected fields of research: geophysics [189], meteorology and climate modeling [216]. In this last research category, global circulation models are used as boundary conditions to more specific (lower-scale) models, with improved micro-physics. In this way, spectral methods are only a part of the global numerical model, combined with other techniques to bring the highest accuracy, for a given computational power. A solution to the Maxwell equations can, of course, also be obtained with spectral methods and therefore, magneto-hydrodynamics (MHD) have been studied with these techniques (see, e.g., Hollerbach [119]). This has been the case in astrophysics too, where, for example, spectral three-dimensional numerical models of solar magnetic dynamo action realized by turbulent convection have been computed [52]. And Kompaneet’s equation, describing the evolution of photon distribution function in a plasma bath at thermal equilibrium within the Fokker-Planck approximation, has been solved using spectral methods to model the X-ray emission of Her X-1 [33, 40]. In simulations of cosmological structure formation or galaxy evolution, many N-body codes rely on a spectral solver for the computation of the gravitational force by the particle-mesh algorithm. The mass corresponding to each particle is decomposed onto neighboring grid points, thus defining a density field. The Poisson equation giving the Newtonian gravitational potential is then usually solved in Fourier space for both fields [118].

To our knowledge, the first published result of the numerical solution of Einstein’s equations, using spectral methods, is the spherically-symmetric collapse of a neutron star to a black hole by Gourgoulhon in 1991 [95]. He used spectral methods as they were developed in the Meudon group by Bonazzola and Marck [44]. Later studies of quickly-rotating neutron stars [41] (stationary axisymmetric models), the collapse of a neutron star in tensor-scalar theory of gravity [156] (spherically-symmetric dynamic spacetime), and quasiequilibrium configurations of neutron star binaries [39] and of black holes [110] (three-dimensional and stationary spacetimes) have grown in complexity, up to the three-dimensional time-dependent numerical solution of Einstein’s equations [37]. On the other hand, the first fully three-dimensional evolution of the whole Einstein system was achieved in 2001 by Kidder et al. [127], where a single black hole was evolved to t ≃ 600 M − 1300 M using excision techniques. They used spectral methods as developed in the Cornell/Caltech group by Kidder et al. [125] and Pfeiffer et al. [171]. Since then, they have focused on the evolution of black-hole-binary systems, which has recently been simulated up to merger and ring down by Scheel et al. [185]. Other groups (for instance Ansorg et al. [10], Bartnik and Norton [21], Frauendiener [81] and Tichy [219]) have also used spectral methods to solve Einstein’s equations; Sections 5 and 6 are devoted to a more detailed review of these works.

1.3 A simple example

Before entering the details of spectral methods in Sections 2, 3 and 4, let us give here their spirit with the simple example of the Poisson equation in a spherical shell:

$$\Delta \phi = \sigma,$$

(7)

where Δ is the Laplace operator (93) expressed in spherical coordinates (r, θ, φ) (see also Section 3.2). We want to solve Equation (7) in the domain where 0 < R_min ≤ r ≤ R_max, θ ∈ [0, π], φ ∈ [0, 2π). This Poisson equation naturally arises in numerical relativity when, for example, solving for initial conditions or the Hamiltonian constraint in the 3+1 formalism [97]: the linear part of these equations can be cast in form (7), and the nonlinearities put into the source σ, with an iterative scheme on ϕ.

First, the angular parts of both fields are decomposed into a (finite) set of spherical harmonics $\{Y_\ell ^m\}$ (see Section 3.2.2):

$$\sigma (r,\theta, \varphi) \simeq \sum\limits_{\ell = 0}^{{\ell _{\max}}} {\sum\limits_{m = - \ell}^{m = \ell} {{s_{\ell m}}(r)Y_\ell ^m(\theta, \varphi)}},$$

(8)

with a similar formula relating ϕ to the radial functions f_ℓm(r). Because spherical harmonics are eigenfunctions of the angular part of the Laplace operator, the Poisson equation can be equivalently solved as a set of ordinary differential equations for each couple (ℓ, m), in terms of the coordinate r:

$$\forall (\ell, m),\quad {{{d^2}{f_{\ell m}}} \over {d{r^2}}} + {2 \over r}{{d{f_{\ell m}}} \over {dr}} - {{\ell (\ell + 1){f_{\ell m}}} \over {{r^2}}} = {s_{\ell m}}(r).$$

(9)

We then map

$$\begin{array}{*{20}c} {[{R_{\min}},{R_{\max}}] \rightarrow [ - 1,1]\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ {r \mapsto \xi = {{2r - {R_{\max}} - {R_{\min}}} \over {{R_{\max}} - {R_{\min}}}},}\\\end{array}$$

(10)

and decompose each field in a (finite) basis of Chebyshev polynomials {T_i}_i=0…N (see Section 2.4.3):

$$\begin{array}{*{20}c} {{s_{\ell m}}(\xi) = \sum\limits_{i = 0}^N {{c_{i\ell m}}{T_i}(\xi),}}\\ {{f_{\ell m}}(\xi) = \sum\limits_{i = 0}^N {{a_{i\ell m}}{T_i}(\xi){.}}}\\ \end{array}$$

(11)

Each function f_ℓm(r) can be regarded as a column-vector A_ℓm of its N + 1 coefficients a_iℓm in this basis; the linear differential operator on the left-hand side of Equation (9) being, thus, a matrix L_ℓm acting on the vector:

$${L_{\ell m}}{A_{\ell m}} = {S_{\ell m}},$$

(12)

with S_ℓm being the vector of the N +1 coefficients c_iℓm of s_ℓm(r). This matrix can be computed from the recurrence relations fulfilled by the Chebyshev polynomials and their derivatives (see Section 2.4.3 for details).

The matrix L is singular because problem (7) is ill posed. One must indeed specify boundary conditions at r = R_min and r = R_max. For simplicity, let us suppose

$$\forall (\theta, \varphi),\quad \phi (r = {R_{\min}},\theta, \varphi) = \phi (r = {R_{\max}},\theta, \varphi) = 0{.}$$

(13)

To impose these boundary conditions, we adopt the tau methods (see Section 2.5.2): we build the matrix ${\bar L}$, taking L and replacing the last two lines by the boundary conditions, expressed in terms of the coefficients from the properties of Chebyshev polynomials:

$$\forall (\ell, m),\quad \sum\limits_{i = 0}^N {{{(- 1)}^i}{a_{i\ell m}} =} \sum\limits_{i = 0}^N {{a_{i\ell m}}} = 0.$$

(14)

Equations (14) are equivalent to boundary conditions (13), within the considered spectral approximation, and they represent the last two lines of ${\bar L}$, which can now be inverted and give the coefficients of the solution ϕ.

If one summarizes the steps:

• 1. Setup an adapted grid for the computation of spectral coefficients (e.g., equidistant in the angular directions and Chebyshev-Gauss-Lobatto collocation points; see Section 2.4.3).

• 2. Get the values of the source σ on these grid points.

• 3. Perform a spherical-harmonics transform (for example, using some available library [151]), followed by the Chebyshev transform (using a Fast Fourier Transform (FFT), or a Gauss-Lobatto quadrature) of the source σ.

• 4. For each couple of values (ℓ, m), build the corresponding matrix ${\bar L}$ with the boundary conditions, and invert the system (using any available linear-algebra package) with the coefficients of as the right-hand side.

• 5. Perform the inverse spectral transform to get the values of ϕ on the grid points from its coefficients.

A numerical implementation of this algorithm has been reported by Grandclément et al. [109], who have observed that the error decayed as ${e^{- {\ell _{\max}}}} \cdot {e^{- N}}$, provided that the source σ was smooth. Machine round-off accuracy can be reached with ℓ_max ∼ N ∼ 30, which makes the matrix inversions of step 4 very cheap in terms of CPU and the whole method affordable in terms of memory usage. These are the main advantages of using spectral methods, as shall be shown in the following sections.

2 Concepts in One Dimension

In this section the basic concept of spectral methods in one spatial dimension is presented. Some general properties of the approximation of functions by polynomials are introduced. The main formulae of the spectral expansion are then given and two sets of polynomials are discussed (Legendre and Chebyshev polynomials). A particular emphasis is put on convergence properties (i.e., the way the spectral approximation converges to the real function).

In Section 2.5, three different methods of solving an ordinary differential equation (ODE) are exhibited and applied to a simple problem. Section 2.6 is concerned with multidomain techniques. After giving some motivations for the use of multidomain decomposition, four different implementations are discussed, as well as their respective merits. One simple example is given, which uses only two domains.

For problems in more than one dimension see Section 3.

2.1 Best polynomial approximation

Polynomials are the only functions that a computer can exactly evaluate and so it is natural to try to approximate any function by a polynomial. When considering spectral methods, we use global polynomials on a few domains. This is to be contrasted with finite difference schemes, for instance, where only local polynomials are considered.

In this particular section, real functions of [−1, 1] are considered. A theorem due to Weierstrass (see for instance [65]) states that the set ℙ of all polynomials is a dense subspace of all the continuous functions on [−1, 1], with the norm ∥·∥_∞. This maximum norm is defined as

$${\left\Vert f \right\Vert_\infty} = {\max\limits_{x \in [ - 1,1]}}\vert f(x)\vert.$$

(15)

This means that, for any continuous function f of [−1, 1], there exists a sequence of polynomials (p_i), i ∈ ℕ that converges uniformly towards f:

$$\underset{i \rightarrow \infty}{\lim} \left\Vert f - {p_i}\right\Vert_{\infty} = 0.$$

(16)

This theorem shows that it is probably a good idea to approximate continuous functions by polynomials.

Given a continuous function f, the best polynomial approximation of degree N, is the polynomial $p_N^{\ast}$ that minimizes the norm of the difference between f and itself:

$${\left\Vert {f - p_N^\star} \right\Vert_\infty} = \min \left\{{\left\Vert {f - p} \right\Vert_\infty},p \in {{\mathbb P}_N}\right\}{.}$$

(17)

Chebyshev alternate theorem states that for any continuous function f, $p_N^{\ast}$ is unique (theorem 9.1 of [178] and theorem 23 of [149]). There exist N + 2 points x_i ∈ [−1, 1] such that the error is exactly attained at those points in an alternate manner:

$$f({x_i}) - p_N^\star({x_i}) = {(- 1)^{i + \delta}}{\left\Vert {f - p_N^ \star} \right\Vert_\infty},$$

(18)

where δ = 0 or δ = 1. An example of a function and its best polynomial approximation is shown in Figure 1.

Figure 1

Function f = cos³ (πx/2) + (x + 1)³/8 (black curve) and its best approximation of degree 2 (red curve). The blue arrows denote the four points where the maximum error is attained.

2.2 Interpolation on a grid

A grid X on the interval [−1, 1] is a set of N + 1 points x_i ∈ [−1, 1], 0 ≤ i ≤ N. These points are called the nodes of the grid X.

Let us consider a continuous function f and a family of grids X with N + 1 nodes x_i. Then, there exists a unique polynomial of degree N, $I_N^Xf$, that coincides with f at each node:

$$I_N^Xf({x_i}) = f({x_i})\quad 0 \leq i \leq N.$$

(19)

$I_N^Xf$ is called the interpolant of f through the grid X. $I_N^Xf$ can be expressed in terms of the Lagrange cardinal polynomials:

$$I_N^Xf = \sum\limits_{i = 0}^N {f({x_i})} \ell _i^X(x),$$

(20)

where $\ell _i^X$ are the Lagrange cardinal polynomials. By definition, $\ell _i^X$ is the unique polynomial of degree N that vanishes at all nodes of the grid X, except at x_i, where it is equal to one. It is easy to show that the Lagrange cardinal polynomials can be written as

$$\ell _i^X(x) = \prod\limits_{j = 0,j \neq i}^N {{{x - {x_j}} \over {{x_i} - {x_j}}}.}$$

(21)

Figure 2 shows some examples of Lagrange cardinal polynomials. An example of a function and its interpolant on a uniform grid can be seen in Figure 3.

Figure 2

Lagrange cardinal polynomials $\ell _3^X$ (red curve) and $\ell _7^X$ on an uniform grid with N = 8. The black circles denote the nodes of the grid.

Figure 3

Function f = cos³ (πx/2) + (x +1)³/8 (black curve) and its interpolant (red curve)on a uniform grid of five nodes. The blue circles show the position of the nodes.

Thanks to Chebyshev alternate theorem, one can see that the best approximation of degree N is an interpolant of the function at N + 1 nodes. However, in general, the associated grid is not known. The difference between the error made by interpolating on a given grid X can be compared to the smallest possible error for the best approximation. One can show that (see Prop. 7.1 of [178]):

$${\left\Vert {f - I_N^Xf} \right\Vert _\infty} \leq (1 + {\Lambda _N}(X)){\left\Vert {f - p_N^\star} \right\Vert _\infty},$$

(22)

where Λ is the Lebesgue constant of the grid X and is defined as:

$${\Lambda _N}(X) = {\max _{x \in [ - 1,1]}}\sum\limits_{i = 0}^N {\vert \ell _i^X(x)\vert.}$$

(23)

A theorem by Erdös [72] states that, for any choice of grid X, there exists a constant C > 0 such that:

$${\Lambda _N}(X) > {2 \over \pi}\ln (N + 1) - C.$$

(24)

It immediately follows that Λ_N → ∞ when N → ∞. This is related to a result from 1914 by Faber [73] that states that for any grid, there always exists at least one continuous function f, whose interpolant does not converge uniformly to f. An example of such failure of convergence is show in Figure 4, where the convergence of the interpolant to the function $f = {1 \over {1 + 16{x^2}}}$ is clearly nonuniform (see the behavior near the boundaries of the interval). This is known as the Runge phenomenon.

Figure 4

Function $f = {1 \over {1 + 16{x^2}}}$ (black curve) and its interpolant (red curve) on a uniform grid of five nodes (left panel) and 14 nodes (right panel). The blue circles show the position of the nodes.

Moreover, a theorem by Cauchy (theorem 7.2 of [178]) states that, for all functions $f \in {{\mathcal C}^{(N + 1)}}$, the interpolation error on a grid X of N + 1 nodes is given by

$$f(x) - I_N^Xf(x) = {{{f^{N + 1}}(\epsilon)} \over {(N + 1)!}}w_{N + 1}^X(x),$$

(25)

where ϵ ∊ [−1, 1]. $w_{N + 1}^X$ is the nodal polynomial of X, being the only polynomial of degree N + 1, with a leading coefficient of 1, and that vanishes on the nodes of X. It is then easy to show that

$$w_{N + 1}^X(x) = \prod\limits_{i = 0}^N {(x - {x_i}).}$$

(26)

In Equation (25), one has a priori no control on the term involving f^{N + 1}. For a given function, it can be rather large and this is indeed the case for the function f shown in Figure 4 (one can check, for instance, that ∣f^N+1 (1)∣ becomes larger and larger). However, one can hope to minimize the interpolation error by choosing a grid such that the nodal polynomial is as small as possible. A theorem by Chebyshev states that this choice is unique and is given by a grid, whose nodes are the zeros of the Chebyshev polynomial T_N+1 (see Section 2.3 for more details on Chebyshev polynomials). With such a grid, one can achieve

$${\left\Vert {w_{N + 1}^X} \right\Vert _\infty} = {1 \over {{2^N}}},$$

(27)

which is the smallest possible value (see Equation (18), Section 4.2, Chapter 5 of [122]). So, a grid based on nodes of Chebyshev polynomials can be expected to perform better that a standard uniform one. This is what can be seen in Figure 5, which shows the same function and its interpolants as in Figure 4, but with a Chebyshev grid. Clearly, the Runge phenomenon is no longer present. One can check that, for this choice of function f, the uniform convergence of the interpolant to the function is recovered. This is because $\Vert w_{N + 1}^X{\Vert _\infty}$ decreases faster than f^N+1/(N + 1)! increases. Of course, Faber’s result implies that this cannot be true for all the functions. There still must exist some functions for which the interpolant does not converge uniformly to the function itself (it is actually the class of functions that are not absolutely continuous, like the Cantor function).

Figure 5

Same as Figure 4 but using a grid based on the zeros of Chebyshev polynomials. The Runge phenomenon is no longer present.

2.3 Polynomial interpolation

2.3.1 Orthogonal polynomials

Spectral methods are often based on the notion of orthogonal polynomials. In order to define orthogonality, one must define the scalar product of two functions on an interval [−1, 1]. Let us consider a positive function w of [−1, 1] called the measure. The scalar product of f and g with respect to this measure is defined as:

$${(f,g)_w} = \int\nolimits_{x \in [ - 1,1]} f (x)g(x)w(x){\rm{d}}x.$$

(28)

A basis of P_ℕ is then a set of N + 1 polynomials {p_n}_n=0…n · p_n is of degree n and the polynomials are orthogonal: (p_i, p_j)_w = 0 for i ≠ j.

The projection P_Nf of a function f on this basis is then

$${P_N}f = \sum\limits_{n = 0}^N {{{\hat f}_n}{p_n},}$$

(29)

where the coefficients of the projection are given by

$${\hat f_n} = {{(f,{p_n})} \over {({p_n},{p_n})}}.$$

(30)

The difference between f and its projection goes to zero when N increases:

$${\left\Vert {f - {P_N}f} \right\Vert _\infty} \rightarrow 0\quad {\rm{when}}\quad N \rightarrow \infty.$$

(31)

Figure 6 shows the function f = cos³ (πx/2) + (x + 1)³/8 and its projection on Chebyshev polynomials (see Section 2.4.3) for N = 4 and N = 8, illustrating the rapid convergence of P_Nf to f.

Figure 6

Function f = cos³ (πx/2) + (x + 1)³/8 (black curve) and its projection on Chebyshev polynomials (red curve), for N = 4 (left panel) and N = 8 (right panel).

At first sight, the projection seems to be an interesting means of numerically representing a function. However, in practice this is not the case. Indeed, to determine the projection of a function, one needs to compute the integrals (30), which requires the evaluation of at a great number of points, making the whole numerical scheme impractical.

2.3.2 Gaussian quadratures

The main theorem of Gaussian quadratures (see for instance [57]) states that, given a measure w, there exist N + 1 positive real numbers w_n and N + 1 real numbers x_n ∈ [−1, 1] such that:

$$\forall f \in {{\mathbb P}_{2N + \delta}},\quad \int\nolimits_{[ - 1,1]} {f(x)w(x){\rm{d}}x = \sum\limits_{n = 0}^N {f({x_n}){w_n}.}}$$

(32)

The w_n are called the weights and the x_n are the collocation points. The integer δ can take several values depending on the exact quadrature considered:

• Gauss quadrature: δ = 1.

• Gauss-Radau: δ = 0 and x₀ = −1.

• Gauss-Lobatto: δ = −1 and x₀ = −1, x_N = 1.

Gauss quadrature is the best choice because it applies to polynomials of higher degree but Gauss-Lobatto quadrature is often more useful for numerical purposes because the outermost collocation points coincide with the boundaries of the interval, making it easier to impose matching or boundary conditions. More detailed results and demonstrations about those quadratures can be found for instance in [57].

2.3.3 Spectral interpolation

As already stated in 2.3.1, the main drawback of projecting a function in terms of orthogonal polynomials comes from the difficulty to compute the integrals (30). The idea of spectral methods is to approximate the coefficients of the projection by making use of Gaussian quadratures. By doing so, one can define the interpolant of a function f by

$${I_N}f = \sum\limits_{n = 0}^N {{{\tilde f}_n}{p_n}(x),}$$

(33)

where

$${\tilde f_n} = {1 \over {{\gamma _n}}}\sum\limits_{i = 0}^N {f({x_i}){p_n}({x_i}){w_i}\quad {\rm{and}}\quad {\gamma _n} = \sum\limits_{i = 0}^N {p_n^2({x_i}){w_i}}.}$$

(34)

The ${{\tilde f}_n}$ exactly coincides with the coefficients ${{\hat f}_n}$, if the Gaussian quadrature is applicable for computing Equation (30), that is, for all f ∈ ℙ_N+δ. So, in general, I_Nf ≠ P_Nf and the difference between the two is called the aliasing error. The advantage of using ${{\tilde f}_n}$ is that they are computed by estimating f at the N + 1 collocation points only.

One can show that I_Nf and f coincide at the collocation points: I_Nf(x_i) = f(x_i) so that I_N interpolates f on the grid, whose nodes are the collocation points. Figure 7 shows the function f = cos³(π/2) + (x + 1)³/8 and its spectral interpolation using Chebyshev polynomials, for N = 4 and N = 6.

Figure 7

Function f = cos³ (πx/2) + (x + 1)³/8 (black curve) and its interpolant I_Nf on Chebyshev polynomials (red curve), for N = 4 (left panel) and N = 6 (right panel). The collocation points are denoted by the blue circles and correspond to Gauss-Lobatto quadrature.

2.3.4 Two equivalent descriptions

The description of a function f in terms of its spectral interpolation can be given in two different, but equivalent spaces:

• in the configuration space, if the function is described by its value at the N + 1 collocation points f(x_i);

• in the coefficient space, if one works with the N + 1 coefficients ${{\tilde f}_i}$.

There is a bijection between both spaces and the following relations enable us to go from one to the other:

• the coefficients can be computed from the values of f(x_i) using Equation (34);

• the values at the collocation points are expressed in terms of the coefficients by making use of the definition of the interpolant (33):

  $$f({x_i}) = \sum\limits_{n = 0}^N {{{\tilde f}_n}{p_n}({x_i}).}$$

  (35)

Depending on the operation one has to perform on a given function, it may be more clever to work in one space or the other. For instance, the square root of a function is very easily given in the collocation space by $\sqrt {f({x_i})}$, whereas the derivative can be computed in the coefficient space if, and this is generally the case, the derivatives of the basis polynomials are known, by ${f^{\prime}}(x) = \sum\limits_{n = 0}^N {{{\tilde f}_n}{p^{\prime}}_n(x)}$.

2.4 Usual polynomials

2.4.1 Sturm-Liouville problems and convergence

The Sturm-Liouville problems are eigenvalue problems of the form:

$$- (pu^{\prime})^{\prime} + qu = \lambda wu,$$

(36)

on the interval [−1, 1]. p, q and w are real-valued functions such that:

• p(x) is continuously differentiable, strictly positive and continuous at x = ±1.

• q(x) is continuous, non-negative and bounded.

• w(x) is continuous, non-negative and integrable.

The solutions are then the eigenvalues λ_i and the eigenfunctions u_i(x). The eigenfunctions are orthogonal with respect to the measure w:

$$\int\nolimits_{- 1}^1 {{u_m}(x){u_n}} (x)w(x){\rm{d}}x = 0\quad {\rm{for}}\quad m \neq n.$$

(37)

Singular Sturm-Liouville problems are particularly important for spectral methods. A Sturm-Liouville problem is singular if and only if the function p vanishes at the boundaries x = ±1. One can show, that if the functions of the spectral basis are chosen to be the solutions of a singular Sturm-Liouville problem, then the convergence of the function to its interpolant is faster than any power law of N, N being the order of the expansion (see Section 5.2 of [57]). One talks about spectral convergence. Let us be precise in saying that this does not necessarily imply that the convergence is exponential. Convergence properties are discussed in more detail for Legendre and Chebyshev polynomials in Section 2.4.4.

Conversely, it can be shown that spectral convergence is not ensured when considering solutions of regular Sturm-Liouville problems [57].

In what follows, two usual types of solutions of singular Sturm-Liouville problems are considered: Legendre and Chebyshev polynomials.

2.4.2 Legendre polynomials

Legendre polynomials P_n are eigenfunctions of the following singular Sturm-Liouville problem:

$$((1 - {x^2})P_n^\prime)^\prime + n(n + 1){P_n} = 0.$$

(38)

In the notations of Equation (36), p = 1 − x², q = 0, w = 1 and λ_n = −n(n + 1).

It follows that Legendre polynomials are orthogonal on [−1, 1] with respect to the measure w(x) = 1. Moreover, the scalar product of two polynomials is given by:

$$({P_n},{P_m}) = \int\nolimits_{- 1}^1 {{P_n}{P_m}{\rm{d}}x = {2 \over {2n + 1}}{\delta _{mn}}.}$$

(39)

Starting from P₀ = 1 and P₁ = x, the successive polynomials can be computed by the following recurrence expression:

$$(n + 1)\;{P_{n + 1}}\;(x) = (2n + 1)\;x{P_n}\;(x) - n{P_{n - 1}}\;(x).$$

(40)

Among the various properties of Legendre polynomials, one can note that i) P_n has the same parity as n. ii) P_n is of degree n. iii) P_n(±1) = (±1)ⁿ. iv) P_n has exactly n zeros on [−1, 1]. The first polynomials are shown in Figure 8.

Figure 8

First Legendre polynomials, from P₀ to P₅.

The weights and locations of the collocation points associated with Legendre polynomials depend on the choice of quadrature.

• Legendre-Gauss: x_i are the nodes of P_N+1 and ${w_i} = {2 \over {(1 - x_i^2){{[P_{N - 1}^{\prime}({x_i})]}^2}}}$.

• Legendre-Gauss-Radau: x₀ = −1 and x_i are the nodes of P_N + P_N+1. The weights are given by ${w_0} = {2 \over {{{(N + 1)}^2}}}$ and ${w_i} = {1 \over {{{(N + 1)}^2}}}$.

• Legendre-Gauss-Lobatto: x₀ = −1, x_N = 1 and x_i are the nodes of P′_N. The weights are ${w_i} = {2 \over {N(N + 1)}}{1 \over {{{[{P_N}({x_i})]}^2}}}$.

These values have no analytic expression, but they can be computed numerically in an efficient way.

Some elementary operations can easily be performed on the coefficient space. Let us assume that a function f is given by its coefficients a_n so that $f = \sum\limits_{n = 0}^N {{a_n}{P_n}}$. Then, the coefficients b_n of $Hf = \sum\limits_{n = 0}^N {{b_n}{P_n}}$ can be found as a function of a_n, for various operators H. For instance,

• if is multiplication by x then:

  $${b_n} = {n \over {2n - 1}}{a_{n - 1}} + {{n + 1} \over {2n + 3}}{a_{n + 1}}\quad (n \geq 1);$$

  (41)

• if is the derivative:

  $${b_n} = (2n + 1)\sum\limits_{p = n + 1,p + n\;{\rm{odd}}}^N {{a_p}};$$

  (42)

• if is the second derivative:

  $${b_n} = (n + 1/2)\sum\limits_{p = n + 2,p + n\;{\rm{even}}}^N {[p(p + 1) - n(n + 1)]{a_p}}.$$

  (43)

These kind of relations enable one to represent the action of H as a matrix acting on the vector of a_n, the product being the coefficients of Hf, i.e. the b_n.

2.4.3 Chebyshev polynomials

Chebyshev polynomials T_n are eigenfunctions of the following singular Sturm-Liouville problem:

$$\left({\sqrt {1 - {x^2}} T_n^\prime} \right)^\prime + {n \over {\sqrt {1 - {x^2}}}}{T_n} = 0.$$

(44)

In the notation of Equation (36), $p = \sqrt {1 - {x^2}}, q = 0,\omega = 1/\sqrt {1 - {x^2}}$ and λ_n = −n.

It follows that Chebyshev polynomials are orthogonal on [−1, 1] with respect to the measure $w = 1/\sqrt {1 - {x^2}}$ and the scalar product of two polynomials is

$$({T_n},{T_m}) = \int\nolimits_{- 1}^1 {{{{T_n}{T_m}} \over {\sqrt {1 - {x^2}}}}{\rm{d}}x = {\pi \over 2}(1 + {\delta _{0n}}){\delta _{mn}}}.$$

(45)

Given that T₀ = 1 and T₁ = x, the higher-order polynomials can be obtained by making use of the recurrence

$${T_{n + 1}}(x) = 2x{T_n}(x) - {T_{n - 1}}(x).$$

(46)

This implies the following simple properties: i) T_n has the same parity as n; ii) T_n is of degree n; iii) T_n(±1) = (±1)ⁿ; iv) T_n has exactly n zeros on [−1, 1]. The first polynomials are shown in Figure 9.

Figure 9

First Chebyshev polynomials, from T₀ to T₅.

Contrary to the Legendre case, both the weights and positions of the collocation points are given by analytic formulae:

• Chebyshev-Gauss: ${x_i} = \cos {{(2i + 1)\pi} \over {2N + 2}}$ and ${w_i} = {\pi \over {N + 1}}$.

• Chebyshev-Gauss-Radau: ${x_i} = \cos {{2\pi i} \over {2N + 1}}$. The weights are ${w_0} = {\pi \over {2N + 1}}$ and ${w_i} = {{2\pi} \over {2N + 1}}$.

• Chebyshev-Gauss-Lobatto: ${x_i} = \cos {{\pi i} \over N}$. The weights are ${w_0} = {w_N} = {\pi \over {2N}}$ and ${w_i} = {\pi \over N}$.

As for the Legendre case, the action of various linear operators H can be expressed in the coefficient space. This means that the coefficients b_n of Hf are given as functions of the coefficients a_n of f. For instance,

• if is multiplication by x:

  $${b_n} = {1 \over 2}[(1 + {\delta _{0\;n - 1}}){a_{n - 1}} + {a_{n + 1}}]\quad (n \geq 1);$$

  (47)

• if H is the derivative:

  $${b_n} = {2 \over {(1 + {\delta _{0\;n}})}}\sum\limits_{p = n + 1,p + n\;{\rm{odd}}}^N {p{a_p}};$$

  (48)

• if H is the second derivative:

  $${b_n} = {1 \over {(1 + {\delta _{0\;n}})}}\sum\limits_{p = n + 2,p + n\;{\rm{even}}}^N {p({p^2} - {n^2}){a_p}}.$$

  (49)

2.4.4 Convergence properties

One of the main advantages of spectral methods is the very fast convergence of the interpolant I_Nf to the function f, at least for smooth enough functions. Let us consider a ${{\mathcal C}^m}$ function f; one can place the following upper bounds on the difference between f and its interpolant I_Nf:

• For Legendre:

  $${\left\Vert {{I_N}f - f} \right\Vert _{{L^2}}} \leq {{{C_1}} \over {{N^{m - 1/2}}}}\sum\limits_{k = 0}^m {{{\left\Vert {{f^{(k)}}} \right\Vert}_{{L^2}}}}.$$

  (50)

• For Chebyshev:

  $${\left\Vert {{I_N}f - f} \right\Vert _{L_w^2}} \leq {{{C_2}} \over {{N^m}}}\sum\limits_{k = 0}^m {{{\left\Vert {{f^{(k)}}} \right\Vert}_{L_w^2}}}.$$

  (51)
  $${\left\Vert {{I_N}f - f} \right\Vert _\infty} \leq {{{C_3}} \over {{N^{m - 1/2}}}}\sum\limits_{k = 0}^m {{{\left\Vert {{f^{(k)}}} \right\Vert}_{L_w^2}}}.$$

  (52)

The C_i are positive constants. An interesting limit of the above estimates concerns a ${{\mathcal C}^\infty}$ function. One can then see that the difference between f and I_Nf decays faster than any power of N. This is spectral convergence. Let us be precise in saying that this does not necessarily imply that the error decays exponentially (think about exp $\left({- \sqrt N} \right)$ for instance). Exponential convergence is achieved only for analytic functions, i.e. functions that are locally given by a convergent power series.

An example of this very fast convergence is shown in Figure 10. The error clearly decays exponentially, the function being analytic, until it reaches the level of machine precision, 10⁻¹⁴ (one is working in double precision in this particular case). Figure 10 illustrates the fact that, with spectral methods, very good accuracy can be reached with only a moderate number of coefficients.

Figure 10

Maximum difference between f = cos³ (πx/2) + (x + 1)³/8 and its interpolant I_Nf, as a function of N.

If the function is less regular (i.e. not ${{\mathcal C}^\infty}$), the error only decays as a power law, thus making the use of spectral method less appealing. It can easily be seen in the worst possible case: that of a discontinuous function. In this case, the estimates (50–52) do not even ensure convergence. Figure 11 shows a step function and its interpolant for various values of N. One can see that the maximum difference between the function and its interpolant does not go to zero even when N is increasing. This is known as the Gibbs phenomenon.

Figure 11

Step function (black curve) and its interpolant, for various values of N.

Finally, Equation (52) shows that, if m > 0, the interpolant converges uniformly to the function. Continuous functions that do not converge uniformly to their interpolant, whose existence has been shown by Faber [73] (see Section 2.2), must belong to the ${{\mathcal C}^0}$ functions. Indeed, for the case m = 0, Equation (52) does not prove convergence (neither do Equations (50) or (51)).

2.4.5 Trigonometric functions

A detailed presentation of the theory of Fourier transforms is beyond the scope of this work. However, there is a close link between discrete Fourier transforms and their spectral interpolation, which is briefly outlined here. More detail can be found, for instance, in [57].

The Fourier transform of a function of [0, 2] is given by:

$$Pf(x) = {a_0} + \sum\limits_{n = 1}^\infty {{a_n}\cos (nx)} + \sum\limits_{n = 1}^\infty {{b_n}\sin (nx).}$$

(53)

The Fourier transform is known to converge rather rapidly to the function itself, if f is periodic. However, the coefficients a_n and b_n are given by integrals of the form $\int\nolimits_0^{2\pi} {f(x)\cos (nx){\rm{d}}x}$, that cannot easily be computed (as was the case for the projection of a function on orthogonal polynomials in Section 2.3.1).

The solution to this problem is also very similar to the use of the Gaussian quadratures. Let us introduce N + 1 collocation points x_i = 2πi/(N + 1). Then the discrete Fourier coefficients with respect to those points are:

$${\tilde a_0} = {1 \over N}\sum\limits_{k = 1}^N {f({x_k}),}$$

(54)

$${\tilde a_n} = {2 \over N}\sum\limits_{k = 1}^N {f({x_k})\cos (n{x_k}),}$$

(55)

$${\tilde b_n} = {2 \over N}\sum\limits_{k = 1}^N {f({x_k})\sin (n{x_k})}$$

(56)

and the interpolant ${I_N}f$ is then given by:

$${I_N}f(x) = {\tilde a_0} + \sum\limits_{n = 1}^N {{{\tilde a}_n}\cos (nx)} + \sum\limits_{n = 1}^N {{{\tilde b}_n}\sin (nx).}$$

(57)

The approximation made by using discrete coefficients in place of real ones is of the same nature as the one made when computing coefficients of projection (30) by means of the Gaussian quadratures. Let us mention that, in the case of a discrete Fourier transform, the first and last collocation points lie on the boundaries of the interval, as for a Gauss-Lobatto quadrature. As for the polynomial interpolation, the convergence of ${I_N}f$ to f is spectral for all periodic and ${{\mathcal C}^\infty}$ functions.

2.4.6 Choice of basis

For periodic functions of [0, 2π], the discrete Fourier transform is the natural choice of basis. If the considered function has also some symmetries, one can use a subset of the trigonometric polynomials. For instance, if the function is i) periodic on [0, 2π] and is also odd with respect to x = π, then it can be expanded in terms of sines only. If the function is not periodic, then it is natural to expand it either in Chebyshev or Legendre polynomials. Using Legendre polynomials can be motivated by the fact that the associated measure is very simple: w(x) = 1. The multidomain technique presented in Section 2.6.5 is one particular example in which such a property is required. In practice, Legendre and Chebyshev polynomials usually give very similar results.

2.5 Spectral methods for ODEs

2.5.1 The weighted residual method

Let us consider a differential equation of the form

$$Lu(x) = S(x),\quad x \in [ - 1,1],$$

(58)

where L is a linear second-order differential operator. The problem admits a unique solution once appropriate boundary conditions are prescribed at x = 1 and x = −1. Typically, one can specify i) the value of u (Dirichlet-type) ii) the value of its derivative ∂_xu (Neumann-type) iii) a linear combination of both (Robin-type).

As for the elementary operations presented in Section 2.4.2 and 2.4.3, the action of L on u can be expressed by a matrix L_ij. If the coefficients of u with respect to a given basis are the ũ_i, then the coefficients of Lu are

$$\sum\limits_{j = 0}^N {{L_{ij}}{{\tilde u}_j}.}$$

(59)

Usually, L_ij can easily be computed by combining the action of elementary operations like the second derivative, the first derivative, multiplication or division by x (see Sections 2.4.2 and 2.4.3 for some examples).

A function u is an admissible solution to the problem if and only if i) it fulfills the boundary conditions exactly (up to machine accuracy) ii) it makes the residual R = Lu − S small. In the weighted residual method, one considers a set of N + 1 test functions {ξ_n}_n=0…N on [−1, 1]. The smallness of R is enforced by demanding that

$$(R,{\xi _k}) = 0,\forall k \leq N.$$

(60)

As N increases, the obtained solution gets closer and closer to the real one. Depending on the choice of the test functions and the way the boundary conditions are enforced, one gets various solvers. Three classical examples are presented below.

2.5.2 The tau method

In this particular method, the test functions coincide with the basis used for the spectral expansion, for instance the Chebyshev polynomials. Let us denote ũ_i and ${{\tilde {\mathcal S}}_i}$ the coefficients of the solution u and of the source $S$, respectively.

Given the expression of Lu in the coefficient space (59) and the fact that the basis polynomials are orthogonal, the residual equations (60) are expressed as

$$\sum\limits_{i = 0}^N {{L_{ni}}{{\tilde u}_i} = {{\tilde s}_n},\quad \forall n \leq N,}$$

(61)

the unknowns being the ũ_i. However, as such, this system does not admit a unique solution, due to the homogeneous solutions of L (i.e. the matrix associated with L is not invertible) and one has to impose boundary conditions. In the tau method, this is done by relaxing the last two equations (61) (i.e. for n = N − 1 and n = N) and replacing them by the boundary conditions at x = −1 and x = 1.

The tau method thus ensures that L_u and S have the same coefficients, excepting the last ones. If the functions are smooth, then their coefficients should decrease in a spectral manner and so the “forgotten” conditions are less and less stringent as N increases, ensuring that the computed solution converges rapidly to the real one.

As an illustration, let us consider the following equation:

$${{{{\rm{d}}^2}u} \over {{\rm{d}}{x^2}}} - 4{{{\rm{d}}u} \over {{\rm{d}}x}} + 4u = \exp (x) - {{4e} \over {(1 + {e^2})}}$$

(62)

with the following boundary conditions:

$$u(x = - 1) = 0\;\;{\rm{and}}\;\;u(x = 1) = 0.$$

(63)

The exact solution is analytic and is given by

$$u(x) = \exp (x) - {{\sinh \;(1)} \over {\sinh \;(2)}}\exp \;(2x) - {e \over {(1 + {e^2})}}.$$

(64)

Figure 12 shows the exact solution and the numerical one, for two different values of N. One can note that the numerical solution converges rapidly to the exact one, the two being almost indistinguishable for N as small as N = 8. The numerical solution exactly fulfills the boundary conditions, no matter the value of N.

Figure 12

Exact solution (64) of Equation (62) (blue curve) and the numerical solution (red curve) computed by means of a tau method, for N = 4 (left panel) and N = 8 (right panel).

2.5.3 The collocation method

The collocation method is very similar to the tau method. They only differ in the choice of test functions. Indeed, in the collocation method one uses continuous functions that are zero at all but one collocation point. They are indeed the Lagrange cardinal polynomials already seen in Section 2.2 and can be written as ξ_i(x_j) = δ_ij. With such test functions, the residual equations (60) are

$$Lu({x_n}) = S({x_n}),\quad \forall n \leq N.$$

(65)

The value of Lu at each collocation point is easily expressed in terms of ũ by making use of (59) and one gets

$$\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{L_{ij}}{{\tilde u}_j}{T_i}}} ({x_n}) = S({x_n}),\quad \forall n \leq N.$$

(66)

Let us note that, even if the collocation method imposes that Lu and S coincide at each collocation point, the unknowns of the system written in the form (66) are the coefficients ũ_n and not u(x_n). As for the tau method, system (66) is not invertible and boundary conditions must be enforced by additional equations. In this case, the relaxed conditions are the two associated with the outermost points, i.e. n = 0 and n = N, which are replaced by appropriate boundary conditions to get an invertible system.

Figure 13 shows both the exact and numerical solutions for Equation (62).

Figure 13

Exact solution (64) of Equation (62) (blue curve) and the numerical solution (red curve) computed by means of a collocation method, for N = 4 (left panel) and N = 8 (right panel).

2.5.4 Galerkin method

The basic idea of the Galerkin method is to seek the solution u as a sum of polynomials G_i that individually verify the boundary conditions. Doing so, u automatically fulfills those conditions and they do not have to be imposed by additional equations. Such polynomials constitute a Galerkin basis of the problem. For practical reasons, it is better to choose a Galerkin basis that can easily be expressed in terms of the original orthogonal polynomials.

For instance, with boundary conditions (63), one can choose:

$${G_{2k}}(x) = {T_{2k + 2}}(x) - {T_0}(x)$$

(67)

$${G_{2k + 1}}(x) = {T_{2k + 3}}(x) - {T_1}(x).$$

(68)

More generally, the Galerkin basis relates to the usual ones by means of a transformation matrix

$${G_i} = \sum\limits_{j = 0}^N {{M_{ji}}{T_j}}, \quad \forall i \leq N - 2.$$

(69)

Let us mention that the matrix M is not square. Indeed, to maintain the same degree of approximation, one can consider only N − 1 Galerkin polynomials, due to the two additional conditions they have to fulfill (see, for instance, Equations (67–68)). One can also note that, in general, the G_i are not orthogonal polynomials.

The solution u is sought in terms of the coefficients $\tilde u_i^G$ on the Galerkin basis:

$$u(x) = \sum\limits_{k = 0}^{N - 2} {\tilde u_k^G{G_k}} (x).$$

(70)

By making use of Equations (59) and (69) one can express Lu in terms of $\tilde u_i^G$:

$$Lu(x) = \sum\limits_{k = 0}^{N - 2} {\tilde u_k^G\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{M_{jk}}{L_{ij}}{T_i}(x).}}}$$

(71)

The test functions used in the Galerkin method are the G_i themselves, so that the residual system reads:

$$(Lu,{G_n}) = (S,{G_n}),\quad \forall n \leq N - 2,$$

(72)

where the left-hand side is computed by means of Equation (71) and by expressing the G_i in terms of the T_i with Equation (69). Concerning the right-hand side, the source itself is not expanded in terms of the Galerkin basis, given that it does not fulfill the boundary conditions. Putting all the pieces together, the Galerkin system reads:

$$\sum\limits_{k = 0}^{N - 2} {\tilde u_k^G\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{M_{in}}{M_{jk}}{L_{ij}}({T_i}\vert {T_i}) = \sum\limits_{i = 0}^N {{M_{in}}{{\tilde s}_i}({T_i}\vert {T_i}),\quad} \forall n \leq N - 2.}}}$$

(73)

This is a system of N − 1 equations for the N − 1 unknowns $\tilde u_i^G$ and it can be directly solved, because it is well posed. Once the $\tilde u_i^G$ are known, one can obtain the solution in terms of the usual basis by making, once again, use of the transformation matrix:

$$u(x) = \sum\limits_{i = 0}^N {\left({\sum\limits_{n = 0}^{N - 2} {{M_{in}}\tilde u_n^G}} \right){T_i}.}$$

(74)

The solution obtained by the application of this method to Equation (62) is shown in Figure 14.

Figure 14

Exact solution (64) of Equation (62) (blue curve) and the numerical solution (red curve) computed by means of the Galerkin method, for N = 4 (left panel) and N = 8 (right panel).

2.5.5 Optimal methods

A spectral method is said to be optimal if it does not introduce an additional error to the error that would be introduced by interpolating the exact solution of a given equation.

Let us call u_exact such an exact solution, unknown in general. Its interpolant is I_Nu_exact and the numerical solution of the equation is u_num. The numerical method is then optimal if and only if $\Vert {I_N}{u_{{\rm{exact}}}} - {u_{{\rm{exact}}}}{\Vert _\infty}$ and $\Vert {u_{{\rm{num}}}} - {u_{{\rm{exact}}}}{\Vert _\infty}$ behave in the same manner when N → ∞.

In general, optimality is difficult to check because both u_exact and its interpolant are unknown. However, for the test problem proposed in Section 2.5.2 this can be done. Figure 15 shows the maximum relative difference between the exact solution (64) and its interpolant and the various numerical solutions. All the curves behave in the same manner as N increases, indicating that the three methods previously presented are optimal (at least for this particular case).

Figure 15

The difference between the exact solution (64) of Equation (62) and its interpolant (black curve) and between the exact and numerical solutions for i) the tau method (green curve and circle symbols) ii) the collocation method (blue curve and square symbols) iii) the Galerkin method (red curve and triangle symbols).

2.6 Multidomain techniques for ODEs

2.6.1 Motivations and setting

As seen in Section 2.4.4, spectral methods are very efficient when dealing with ${{\mathcal C}^\infty}$ functions. However, they lose some of their appeal when dealing with less regular functions, the convergence to the exact functions being substantially slower. Nevertheless, the physicist has sometimes to deal with such functions. This is the case for the density jump at the surface of strange stars or the formation of shocks, to mention only two examples. In order to maintain spectral convergence, one then needs to introduce several computational domains such that the various discontinuities of the functions lie at the interface between the domains. Doing so in each domain means that one only deals with ${{\mathcal C}^\infty}$ functions.

Multidomain techniques can also be valuable when dealing with a physical space either too complicated or too large to be described by a single domain. Related to that, one can also use several domains to increase the resolution in some parts of the space where more precision is required. This can easily be done by using a different number of basis functions in different domains. One then talks about fixed-mesh refinement.

Efficient parallel processing may also require that several domains be used. Indeed, one could set a solver, dealing with each domain on a given processor, and interprocessor communication would then only be used for matching the solution across the various domains. The algorithm of Section 2.6.4 is well adapted to such purposes.

In the following, four different multidomain methods are presented to solve an equation of the type Lu = S on [−1, 1]. L is a second-order linear operator and S is a given source function. Appropriate boundary conditions are given at the boundaries x = −1 and x = 1.

For simplicity the physical space is split into two domains:

• first domain: x ≤ 0 described by x₁ = 2x + 1, x₁ ∈ [−1, 1],

• second domain: x ≥ 0 described by x₂ = 2x − 1, x₂ ∈ [−1, 1].

If x ≤ 0, a function u is described by its interpolant in terms of ${x_1}:{I_N}u(x) = \sum\limits_{i = 0}^N {\tilde u_i^1{T_i}({x_1}(x))}$. The same is true for x ≥ 0 with respect to the variable x₂. Such a set-up is obviously appropriate to deal with problems where discontinuities occur at x = 0, that is x₁ = 1 and x₂ = −1.

2.6.2 The multidomain tau method

As for the standard tau method (see Section 2.5.2) and in each domain, the test functions are the basis polynomials and one writes the associated residual equations. For instance, in the domain x ≤ 0 one gets:

$$({T_n},R) = 0 \Rightarrow \sum\limits_{i = 0}^N {{L_{ni}}\tilde u_i^1 = \tilde s_n^1\quad \forall n \leq N,}$$

(75)

${{\tilde {\mathcal S}}^1}$ being the coefficients of the source and L_ij the matrix representation of the operator. As for the one-domain case, one relaxes the last two equations, keeping only N − 1 equations. The same is done in the second domain.

Two supplementary equations are enforced to ensure that the boundary conditions are fulfilled. Finally, the operator L being of second order, one needs to ensure that the solution and its first derivative are continuous at the interface x = 0. This translates to a set of two additional equations involving both domains.

So, one considers

• N − 1 residual equations in the first domain,

• N − 1 residual equations in the second domain,

• 2 boundary conditions,

• 2 matching conditions,

for a total of 2N + 2 equations. The unknowns are the coefficients of u in both domains (i.e. the $\tilde u_i^1$ and the $\tilde u_i^2$), that is 2N + 2 unknowns. The system is well posed and admits a unique solution.

2.6.3 Multidomain collocation method

As for the standard collocation method (see Section 2.5.3) and in each domain, the test functions are the Lagrange cardinal polynomials. For instance, in the domain x ≤ 0 one gets:

$$\sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{L_{ij}}\tilde u_j^1{T_i}({x_{1n}}) = S({x_{1n}})\quad \forall n \leq N,}}$$

(76)

L_ij being the matrix representation of the operator and x_1n the n^th collocation point in the first domain. As for the one-domain case, one relaxes the two equations corresponding to the boundaries of the domain, keeping only N − 1 equations. The same is done in the second domain.

Two supplementary equations are enforced to ensure that the boundary conditions are fulfilled. Finally, the operator L being second order, one needs to ensure that the solution and its first derivative are continuous at the interface x = 0. This translates to a set of two additional equations involving the coefficients in both domains.

So, one considers

• N − 1 residual equations in the first domain,

• N − 1 residual equations in the second domain,

• 2 boundary conditions,

• 2 matching conditions,

for a total of 2N + 2 equations. The unknowns are the coefficients of u in both domains (i.e. the $\tilde u_i^1$ and the $\tilde u_i^2$), that is 2N + 2 unknowns. The system is well posed and admits a unique solution.

2.6.4 Method based on homogeneous solutions

The method described here proceeds in two steps. First, particular solutions are computed in each domain. Then, appropriate linear combinations with the homogeneous solutions of the operator L are performed to ensure continuity and impose boundary conditions.

In order to compute particular solutions, one can rely on any of the methods described in Section 2.5. The boundary conditions at the boundary of each domain can be chosen (almost) arbitrarily. For instance, one can use in each domain a collocation method to solve Lu = S, demanding that the particular solution u_part is zero at both ends of each interval.

Then, in order to have a solution over the whole space, one needs to add homogeneous solutions to the particular ones. In general, the operator L is second order and admits two independent homogeneous solutions g and h in each domain. Let us note that, in some cases, additional regularity conditions can reduce the number of available homogeneous solutions. The homogeneous solutions can either be computed analytically if the operator L is simple enough or numerically, but one must then have a method for solving Lu = 0.

In each domain, the physical solution is a combination of the particular solution and homogeneous ones of the type:

$$u = {u_{{\rm{part}}}} + \alpha g + \beta h,$$

(77)

where α and β are constants that must be determined. In the two domains case, we are left with four unknowns. The system of equations they must satisfy is composed of i) two equations for the boundary conditions ii) two equations for the matching of u and its first derivative across the boundary between the two domains. The obtained system is called the matching system and generally admits a unique solution.

2.6.5 Variational method

Contrary to previously presented methods, the variational one is only applicable with Legendre polynomials. Indeed, the method requires that the measure be w(x) = 1. It is also useful to extract the second-order term of the operator L and to rewrite it as Lu = u″ + H, H being first order only.

In each domain, one writes the residual equation explicitly:

$$(\xi, R) = 0 \Rightarrow \int {\xi u^{\prime\prime}} {\rm{d}}x + \int \xi (Hu){\rm{d}}x = \int \xi S{\rm{d}}x.$$

(78)

The term involving the second derivative of is then integrated by parts:

$$[\xi u^{\prime}] - \int {\xi ^{\prime}u^{\prime}} {\rm{d}}x + \int \xi (Hu){\rm{d}}x = \int \xi S{\rm{d}}x.$$

(79)

The test functions are the same as the ones used for the collocation method, i.e. functions being zero at all but one collocation point, in both domains (d = 1, 2): ξ_i(x_dj) = δ_ij. By making use of the Gauss quadratures, the various parts of Equation (79) can be expressed as (d = 1, 2 indicates the domain):

$$\int \xi _n^\prime u^\prime{\rm{d}}x = \sum\limits_{i = 0}^N {\int \xi _n^\prime({x_{di}})u^\prime({x_{di}}){w_i} = \sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{D_{ij}}{D_{in}}{w_i}u({x_{dj}}),}}}$$

(80)

$$\int {{\xi _n}} (Hu){\rm{d}}x = \sum\limits_{i = 0}^N {{\xi _n}({x_{di}})(Hu)({x_{di}}){w_i} = {w_n}\sum\limits_{i = 0}^N {{H_{ni}}u({x_{di}})},}$$

(81)

$$\int {{\xi _n}} S{\rm{d}}x = \sum\limits_{i = 0}^N {{\xi _n}({x_{di}})S({x_{di}}){w_i} = S({x_{dn}}){w_n},}$$

(82)

where D_ij (or H_ij, respectively) represents the action of the derivative (or of H, respectively) in the configuration space

$$g^{\prime}({x_{dk}}) = \sum\limits_{j = 0}^N {{D_{kj}}} g({x_{dj}}),$$

(83)

$$(Hg)({x_{dk}}) = \sum\limits_{j = 0}^N {{H_{kj}}} g({x_{dj}}).$$

(84)

For points strictly inside each domain, the integrated term [ξu′] of Equation (79) vanishes and one gets equations of the form:

$$- \sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{D_{ij}}{D_{in}}{w_i}u({x_{dj}}) + {w_n}\sum\limits_{i = 0}^N {{H_{ni}}u({x_{di}}) = S({x_{dn}}){w_n}.}}}$$

(85)

This is a set of N − 1 equations for each domains (d = 1, 2). In the above form, the unknowns are the u. (x_di), i.e. the solution is sought in the configuration space.

As usual, two additional equations are provided by appropriate boundary conditions at both ends of the global domain. One also gets an additional condition by matching the solution across the boundary between the two domains.

The last equation of the system is the matching of the first derivative of the solution. However, instead of writing it “explicitly”, this is done by making use of the integrated term in Equation (79) and this is actually the crucial step of the whole method. Applying Equation (79) to the last point x_1N of the first domain, one gets:

$$u^{\prime}({x_1} = 1) = \sum\limits_{i = 0}^N {\sum\limits_{j = 0}^N {{D_{ij}}{D_{iN}}{w_i}u({x_{1j}}) - {w_N}\sum\limits_{i = 0}^N {{H_{Ni}}u({x_{1i}}) + S({x_{1N}}){w_N}.}}}$$

(86)

The same can be done with the first point of the second domain to get u′(x₂ = −1), and the last equation of the system is obtained by demanding that u′(x₁ = 1) = u’(x₂ = −1) and relates the values of in both domains.

Before finishing with the variational method, it may be worthwhile to explain why Legendre polynomials are used. Suppose one wants to work with Chebyshev polynomials instead. The measure is then $w(x) = {1 \over {\sqrt {1 - {x^2}}}}$. When one integrates the term containing u″ by parts, one gets

$$\int {- u^{\prime\prime}} fw{\rm{d}}x = [ - u^{\prime}fw] + \int {u^{\prime}} f^{\prime}w^{\prime}{\rm{d}}x.$$

(87)

Because the measure is divergent at the boundaries, it is difficult, if not impossible, to isolate the term in u′. On the other hand, this is precisely the term that is needed to impose the appropriate matching of the solution.

2.6.6 Merits of the various methods

From a numerical point of view, the method based on an explicit matching using the homogeneous solutions is somewhat different from the two others. Indeed, one must solve several systems in a row and each one is of the same size as the number of points in one domain. This splitting of the different domains can also be useful for designing parallel codes. On the contrary, for both the variational and the tau method one must solve only one system, but its size is the same as the number of points in a whole space, which can be quite large for many domains settings. However, those two methods do not require one to compute the homogeneous solutions, computation that could be tricky depending on the operators involved and the number of dimensions.

The variational method may seem more difficult to implement and is only applicable with Legendre polynomials. However, on mathematical grounds, it is the only method that is demonstrated to be optimal. Moreover, some examples have been found in which the others methods are not optimal. It remains true that the variational method is very dependent on both the shape of the domains and the type of equation that needs to be solved.

The choice of one method or another thus depends on the particular situation. As for the mono-domain space, for simple test problems the results are very similar. Figure 16 shows the maximum error between the analytic solution and the numeric one for the four different methods. All errors decay exponentially and reach machine accuracy within roughly the same number of points.

Figure 16

Difference between the exact and numerical solutions of the following test problem. ${{{{\rm{d}}^2}u} \over {{\rm{d}}{x^2}}} + 4u = S$, with S(x < 0) = 1 and S(x > 0) = 0. The boundary conditions are u(x = −1) = 0 and u(x = 1) = 0. The black curve and circles denote results from the multidomain tau method, the red curve and squares from the method based on the homogeneous solutions, the blue curve and diamonds from the variational one, and the green curve and triangles from the collocation method.

3 Multidimensional Cases

In principle, the generalization to more than one dimension is rather straightforward if one uses the tensor product. Let us first take an example, with the spectral representation of a scalar function f(x, y) defined on the square (x, y) ∈ [−1, 1] × [−1, 1] in terms of Chebyshev polynomials. One simply writes

$$f(x,y) = \sum\limits_{i = 0}^M {\sum\limits_{j = 0}^N {{a_{ij}}{T_i}(x){T_j}(y),}}$$

(88)

with T_i being the Chebyshev polynomial of degree i. The partial differential operators can also be generalized as being linear operators acting on the space ℙ_M⊗ℙ_N. Simple linear partial differential equations (PDE) can be solved by one of the methods presented in Section 2.5 (Galerkin, tau or collocation), on this MN-dimensional space. The development (88) can of course be generalized to any dimension. Some special PDE and spectral basis examples, where the differential equation decouples for some of the coordinates, will be given in Section 3.2.

3.1 Spatial coordinate systems

Most of the interesting problems in numerical relativity involve asymmetries that require the use of a full set of three-dimensional coordinates. We briefly review several coordinate sets (all orthogonal) that have been used in numerical relativity with spectral methods. They are described through the line element ds² of the flat metric in the coordinates we discuss.

• Cartesian (rectangular) coordinates are of course the simplest and most straightforward to implement; the line element reads ds² = dx² + dy² + dz². These coordinates are regular in all space, with vanishing connection, which makes them easy to use, since all differential operators have simple expressions and the associated triad is also perfectly regular. They are particularly well adapted to cube-like domains, see for instance [167, 171] and [81] in the case of toroidal topology.

• Circular cylindrical coordinates have a line element ds² = dρ² + ρ² dϕ² + dz² and exhibit a coordinate singularity on the z-axis (ρ = 0). The associated triad being also singular for ρ = 0, regular vector or tensor fields have components that are multivalued (depending on ϕ) at any point of the z-axis. As for the spherical coordinates, this can be handled quite easily with spectral methods. This coordinate system can be useful for axisymmetric or rotating systems, see [10].

• Spherical (polar) coordinates will be discussed in more detail in Section 3.2. Their line element reads ds² = dr² + r² dθ² + r² sin² θ dφ², showing a coordinate singularity at the origin (r = 0) and on the axis for which θ = 0, π. They are very useful in numerical relativity for the numerous sphere-like objects under study (stars, black hole horizons) and have mostly been implemented for shell-like domains [40, 109, 167, 219] and for spheres including the origin [44, 109].

• Prolate spheroidal coordinates consist of a system of confocal ellipses and hyperbolae, describing an (x, z)-plane, and an angle φ giving the position as a rotation with respect to the focal axis [131]. The line element is ds² = a²(sinh² μ + sin² ν) (dμ² + dν²) + a² sinh² μ sin² ν dφ². The foci are situated at z = ±a and represent coordinate singularities for μ = 0 and ν = 0, π. These coordinates have been used in [8] with black-hole-puncture data at the foci.

• Bispherical coordinates are obtained by the rotation of bipolar coordinates around the focal axis, with a line element ds² = a² (cosh η − cos χ)⁻² (dη² + dχ² + sin² χdφ²). As with prolate spheroidal coordinates, the foci situated at z = ±a (η → ±∞, χ = 0, π) and more generally, the focal axis, exhibit coordinate singularities. Still, the surfaces of constant are spheres situated in the z > 0(< 0) region for η > 0(< 0), respectively. Thus, these coordinates are very well adapted for the study of binary systems and in particular for excision treatment of black hole binaries [6].

3.1.1 Mappings

Choosing a smart set of coordinates is not the end of the story. As for finite elements, one would like to be able to cover some complicated geometries, like distorted stars, tori, etc… or even to be able to cover the whole space. The reason for this last point is that, in numerical relativity, one often deals with isolated systems for which boundary conditions are only known at spatial infinity. A quite simple choice is to perform a mapping from numerical coordinates to physical coordinates, generalizing the change of coordinates to [−1, 1], when using families of orthonormal polynomials or to [0, 2π] for Fourier series.

An example of how to map the [−1, 1] × [−1, 1] domain can be taken from Canuto et al. [56], and is illustrated in Figure 17: once the mappings from the four sides (boundaries) of ${\hat \Omega}$ to the four sides of Ω are known, one can construct a two-dimensional regular mapping Π, which preserves orthogonality and simple operators (see Chapter 3.5 of [56]).

Figure 17

Regular deformation of the [−1, 1] × [−1, 1] square.

The case where the boundaries of the considered domain are not known at the beginning of the computation can also be treated in a spectral way. In the case where this surface corresponds to the surface of a neutron star, two approaches have been used. First, in Bonazzola et al. [38], the star (and therefore the domain) is supposed to be “star-like”, meaning that there exists a point from which it is possible to reach any point on the surface by straight lines that are all contained inside the star. To such a point is associated the origin of a spherical system of coordinates, so that it is a spherical domain, which is regularly deformed to coincide with the shape of the star. This is done within an iterative scheme, at every step, once the position of the surface has been determined. Then, another approach has been developed by Ansorg et al. [10] using cylindrical coordinates. It is a square in the plane (ρ, z), which is mapped onto the domain describing the interior of the star. This mapping involves an unknown function, which is itself decomposed in terms of a basis of Chebyshev polynomials, so that its coefficients are part of the global vector of unknowns (as the density and gravitational field coefficients).

In the case of black-hole-binary systems, Scheel et al. [188] have developed horizon-tracking coordinates using results from control theory. They define a control parameter as the relative drift of the black hole position, and they design a feedback control system with the requirement that the adjustment they make on the coordinates be sufficiently smooth that they do not spoil the overall Einstein solver. In addition, they use a dual-coordinate approach, so that they can construct a comoving coordinate map, which tracks both orbital and radial motion of the black holes and allows them to successfully evolve the binary. The evolutions simulated in [188] are found to be unstable, when using a single rotating-coordinate frame. We note here as well the work of Bonazzola et al. [42], where another option is explored: the stroboscopic technique of matching between an inner rotating domain and an outer inertial one.

3.1.2 Spatial compactification

As stated above, the mappings can also be used to include spatial infinity into the computational domain. Such a compactification technique is not tied to spectral methods and has already been used with finite-difference methods in numerical relativity by, e.g., Pretorius [176]. However, due to the relatively low number of degrees of freedom necessary to describe a spatial domain within spectral methods, it is easier within this framework to use some resources to describe spatial infinity and its neighborhood. Many choices are possible to do so, either directly choosing a family of well-behaved functions on an unbounded interval, for example the Hermite functions (see, e.g., Section 17.4 in Boyd [48]), or making use of standard polynomial families, but with an adapted mapping. A first example within numerical relativity was given by Bonazzola et al. [41] with the simple inverse mapping in spherical coordinates.

$$r = {1 \over {\alpha (x - 1)}},\quad x \in [ - 1,1].$$

(89)

This inverse mapping for spherical “shells” has also been used by Kidder and Finn [125], Pfeiffer et al. [171, 167], and Ansorg et al. in cylindrical [10] and spheroidal [8] coordinates. Many more elaborated techniques are discussed in Chapter 17 of Boyd [48], but to our knowledge, none have been used in numerical relativity yet. Finally, it is important to point out that, in general, the simple compactification of spatial infinity is not well adapted to solving hyperbolic PDEs and the above mentioned examples were solving only for elliptic equations (initial data, see Section 5). For instance, the simple wave equation (127) is not invariant under the mapping (89), as has been shown, e.g., by Sommerfeld (see [201], Section 23.E). Intuitively, it is easy to see that when compactifying only spatial coordinates for a wave-like equation, the distance between two neighboring grid points becomes larger than the wavelength, which makes the wave poorly resolved after a finite time of propagation on the numerical grid. For hyperbolic equations, is is therefore usually preferable to impose physically and mathematically well-motivated boundary conditions at a finite radius (see, e.g., Friedrich and Nagy [83], Rinne [179] or Buchman and Sarbach [53]).

3.1.3 Patching in more than one dimension

The multidomain (or multipatch) technique has been presented in Section 2.6 for one spatial dimension. In Bonazzola et al. [40] and Grandclément et al. [109], the three-dimensional spatial domains consist of spheres (or star-shaped regions) and spherical shells, across which the solution can be matched as in one-dimensional problems (only through the radial dependence). In general, when performing a matching in two or three spatial dimensions, the reconstruction of the global solution across all domains might need some more care to clearly write down the matching conditions (see, e.g., [167], where overlapping as well as nonoverlapping domains are used at the same time). For example in two dimensions, one of the problems that might arise is the counting of matching conditions for corners of rectangular domains, when such a corner is shared among more than three domains. In the case of a PDE where matching conditions must be imposed on the value of the solution, as well as on its normal derivative (Poisson or wave equation), it is sufficient to impose continuity of either normal derivative at the corner, the jump in the other normal derivative being spectrally small (see Chapter 13 of Canuto et al. [56]).

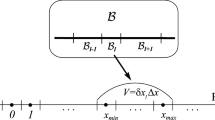
A now typical problem in numerical relativity is the study of binary systems (see also Sections 5.5 and 6.3) for which two sets of spherical shells have been used by Gourgoulhon et al. [100], as displayed in Figure 18. Different approaches have been proposed by Kidder et al. [128], and used by Pfeiffer [167] and Scheel et al. [188] where spherical shells and rectangular boxes are combined together to form a grid adapted to black hole binary study. Even more sophisticated setups to model fluid flows in complicated tubes can be found in [144].

Figure 18

Two sets of spherical domains describing a neutron star or black hole binary system. Each set is surrounded by a compactified domain of the type (89), which is not displayed

Multiple domains can thus be used to adapt the numerical grid to the interesting part (manifold) of the coordinate space; they can be seen as a technique close to the spectral element method [166]. Moreover, it is also a way to increase spatial resolution in some parts of the computational domain where one expects strong gradients to occur: adding a small domain with many degrees of freedom is the analog of fixed-mesh refinement for finite-differences.

3.2 Spherical coordinates and harmonics

Spherical coordinates (see Figure 19) are well adapted for the study of many problems in numerical relativity. Those include the numerical modeling of isolated astrophysical single objects, like a neutron star or a black hole. Indeed, stars’ surfaces have sphere-like shapes and black hole horizons have this topology as well, which is best described in spherical coordinates (eventually through a mapping, see Section 3.1.1). As these are isolated systems in general relativity, the exact boundary conditions are imposed at infinity, requiring a compactification of space, which is here achieved with the compactification of the radial coordinate r only.

Figure 19

Definition of spherical coordinates (r, θ, φ) of a point M and associated triad $({{\vec e}_r},{{\vec e}_\theta},{{\vec e}_\varphi})$, with respect to the Cartesian ones.

When the numerical grid does not extend to infinity, e.g., when solving for a hyperbolic PDE, the boundary defined by r = const is a smooth surface, on which boundary conditions are much easier to impose. Finally, spherical harmonics, which are strongly linked with these coordinates, can simplify a lot the solution of Poisson-like or wave-like equations. On the other hand, there are some technical problems linked with this set of coordinates, as detailed hereafter, but spectral methods can handle them in a very efficient way.

3.2.1 Coordinate singularities

The transformation from spherical (r, θ, φ) to Cartesian coordinates (x, y, z) is obtained by

$$x = r\sin \theta \cos \varphi,$$

(90)

$$y = r\sin \theta \sin \varphi,$$

(91)

$$z = r\cos \theta.$$

(92)

One immediately sees that the origin r = 0 ⇔ x = y = z = 0 is singular in spherical coordinates because neither θ nor φ can be uniquely defined. The same happens for the z-axis, where θ = 0 or π, and φ cannot be defined. Among the consequences is the singularity of some usual differential operators, like, for instance, the Laplace operator

$$\Delta = {{{\partial ^2}} \over {\partial {r^2}}} + {2 \over r}{\partial \over {\partial r}} + {1 \over {{r^2}}}\left({{{{\partial ^2}} \over {\partial {\theta ^2}}} + {1 \over {\tan \theta}}{\partial \over {\partial \theta}} + {1 \over {{{\sin}^2}\theta}}{{{\partial ^2}} \over {\partial {\varphi ^2}}}} \right).$$

(93)

Here, the divisions by r at the center, or by sin θ on the z-axis look singular. On the other hand, the Laplace operator, expressed in Cartesian coordinates, is a perfectly regular one and, if it is applied to a regular function, should give a well-defined result. The same should be true if one uses spherical coordinates: the operator (93) applied to a regular function should yield a regular result. This means that a regular function of spherical coordinates must have a particular behavior at the origin and on the axis, so that the divisions by r or sin θ appearing in regular operators are always well defined. If one considers an analytic function in (regular) Cartesian coordinates f(x, y, z), it can be expanded as a series of powers of x, y and z, near the origin

$$f(x,y,z) = \sum\limits_{n,p,q} {{a_{npq}}} {x^n}{y^p}{z^q}.$$

(94)

Placing the coordinate definitions (90)–(92) into this expression gives

$$f(r, \theta, \varphi) = \sum\limits_{n,p,q} {{a_{npq}}{r^{n + p + q}}{{\cos}^q}\theta {{\sin}^{n + p}}\theta {{\cos}^n}\varphi {{\sin}^p}\varphi;}$$

(95)

and rearranging the terms in φ:

$$f(r, \theta, \varphi) = \sum\limits_{m,p,q} {{b_{mpq}}{r^{\vert m\vert + 2p + q}}{{\sin}^{\vert m\vert + 2p}}\theta {{\cos}^q}\theta {e^{im\varphi}}.}$$

(96)

With some transformations of trigonometric functions in θ, one can express the angular part in terms of spherical harmonics $Y_\ell ^m(\theta, \varphi)$, see Section 3.2.2, with ℓ = ∣m∣ + 2p + q and obtain the two following regularity conditions, for a given couple (ℓ, m):

• near θ = 0, a regular scalar field is equivalent to f(θ) ∼ sin^∣m∣ θ,

• near r = 0, a regular scalar field is equivalent to f(r) ∼ r^ℓ.

In addition, the r-dependence translates into a Taylor series near the origin, with the same parity as ℓ. More details in the case of polar (2D) coordinates are given in Chapter 18 of Boyd [48].

If we go back to the evaluation of the Laplace operator (93), it is now clear that the result is always regular, at least for ℓ ≥ 2 and m ≥ 2. We detail the cases of ℓ = 0 and ℓ =1, using the fact that spherical harmonics are eigenfunctions of the angular part of the Laplace operator (see Equation (103)). For ℓ = 0 the scalar field f is reduced to a Taylor series of only even powers of r, therefore the first derivative contains only odd powers and can be safely divided by r. Once decomposed on spherical harmonics, the angular part of the Laplace operator (93) acting on the ℓ = 1 component reads −2/r², which is a problem only for the first term of the Taylor expansion. On the other hand, this term cancels with the ${2 \over r}{\partial \over {\partial r}}$, providing a regular result. This is the general behavior of many differential operators in spherical coordinates: when applied to a regular field, the full operator gives a regular result, but single terms of this operator may give singular results when computed separately, the singularities canceling between two different terms.

As this may seem an argument against the use of spherical coordinates, let us stress that spectral methods are very powerful in evaluating such operators, keeping everything finite. As an example, we use Chebyshev polynomials in ξ for the expansion of the field f(r = αξ), α being a positive constant. From the Chebyshev polynomial recurrence relation (46), one has

$$\forall n > 0,\quad{{{T_{n + 1}}(\xi)} \over \xi} = 2{T_n}(\xi) - {{{T_{n - 1}}(\xi)} \over \xi},$$

(97)

which recursively gives the coefficients of

$$g(\xi) = {{f(\xi) - f(0)} \over \xi},$$

(98)

from those of f(ξ). The computation of this finite part g(ξ) is always a regular and linear operation on the vector of coefficients. Thus, the singular terms of a regular operator are never computed, but the result is a good one, as if the cancellation of such terms had occurred. Moreover, from the parity conditions it is possible to use only even or odd Chebyshev polynomials, which simplifies the expressions and saves computer time and memory. Of course, relations similar to Equation (97) exist for other families of orthonormal polynomials, as well as relations that divide by sin θ a function developed on a Fourier basis. The combination of spectral methods and spherical coordinates is thus a powerful tool for accurately describing regular fields and differential operators inside a sphere [44]. To our knowledge, this is the first reference showing that it is possible to solve PDEs with spectral methods inside a sphere, including the three-dimensional coordinate singularity at the origin.

3.2.2 Spherical harmonics

Spherical harmonics are the pure angular functions

$$Y_\ell ^m(\theta, \varphi) = \sqrt {{{2\ell + 1} \over {4\pi}}{{(\ell - m)!} \over {(\ell + m)!}}} P_\ell ^m(\cos \theta){e^{im\varphi}},$$

(99)

where ℓ ≥ 0 and ∣m∣ ≤ ℓ. $P_\ell ^m(\cos \theta)$ are the associated Legendre functions defined by

$$P_\ell ^m(x) = {{(\ell + m)!} \over {(\ell - m)!}}{1 \over {{2^\ell}\ell !\sqrt {{{(1 - {x^2})}^m}}}}{{{d^{\ell - m}}} \over {d{x^{\ell - m}}}}{(1 - {x^2})^\ell},$$

(100)

for m ≥ 0. The relation

$$P_\ell ^{- m}(x) = {{(\ell - m)!} \over {(\ell + m)!}}P_\ell ^m(x)$$

(101)

gives the associated Legendre functions for negative m; note that the normalization factors can vary in the literature. This family of functions have two very important properties. First, they represent an orthogonal set of regular functions defined on the sphere; thus, any regular scalar field f(θ, φ) defined on the sphere can be decomposed into spherical harmonics

$$f(\theta, \varphi) = \sum\limits_{\ell = 0}^{+ \infty} {\sum\limits_{m = - \ell}^{m = \ell} {{f_{\ell m}}Y_\ell ^m}} (\theta, \varphi){.}$$

(102)

Since the harmonics are regular, they automatically take care of the coordinate singularity on the z-axis. Then, they are eigenfunctions of the angular part of the Laplace operator (noted here as Δ_θφ):

$$\forall (\ell, m)\;\;{\Delta _{\theta \varphi}}Y_\ell ^m(\theta, \varphi): = {{{\partial ^2}Y_\ell ^m} \over {\partial {\theta ^2}}} + {1 \over {\tan \theta}}{{\partial Y_\ell ^m} \over {\partial \theta}} + {1 \over {{{\sin}^2}\theta}}{{{\partial ^2}Y_\ell ^m} \over {\partial {\varphi ^2}}} = - \ell (\ell + 1)Y_\ell ^m(\theta, \varphi),$$

(103)

the associated eigenvalues being −ℓ(ℓ + 1).

The first property makes the description of scalar fields on spheres very easy: spherical harmonics are used as a decomposition basis within spectral methods, for instance in geophysics or meteorology, and by some groups in numerical relativity [21, 109, 219]. However, they could be more broadly used in numerical relativity, for example for Cauchy-characteristic evolution or matching [228, 15], where a single coordinate chart on the sphere might help in matching quantities. They can also help to describe star-like surfaces being defined by r = h(θ, φ) as event or apparent horizons [152, 23, 1]. The search for apparent horizons is also made easier: since the function h verifies a two-dimensional Poisson-like equation, the linear part can be solved directly, just by dividing by −ℓ(ℓ + 1) in the coefficient space.

The second property makes the Poisson equation,

$$\Delta \phi (r, \theta, \varphi) = \sigma (r, \theta, \varphi),$$

(104)

very easy to solve (see Section 1.3). If the source and the unknown are decomposed into spherical harmonics, the equation transforms into a set of ordinary differential equations for the coefficients (see also [109]):

$$\forall (\ell, m)\;\;\;{{{d^2}{\phi _{\ell m}}} \over {d{r^2}}} + {2 \over r}{{d{\phi _{\ell m}}} \over {dr}} - {{\ell (\ell + 1){\phi _{\ell m}}} \over {{r^2}}} = {\sigma _{\ell m}}.$$

(105)

Then, any ODE solver can be used for the radial coordinate: spectral methods, of course, (see Section 2.5), but others have been used as well (see, e.g., Bartnik et al. [20, 21]). The same technique can be used to advance in time the wave equation with an implicit scheme and Chebyshev-tau method for the radial coordinate [44, 157].

The use of spherical-harmonics decomposition can be regarded as a basic spectral method, like Fourier decomposition. There are, therefore, publicly available “spherical harmonics transforms”, which consist of a Fourier transform in the φ-direction and a successive Fourier and Legendre transform in the θ-direction. A rather efficient one is the SpharmonicsKit/S2Kit [151], but writing one’s own functions is also possible [99].

3.2.3 Tensor components

All the discussion in Sections 3.2.1–3.2.2 has been restricted to scalar fields. For vector, or more generally tensor fields in three spatial dimensions, a vector basis (triad) must be specified to express the components. At this point, it is very important to stress that the choice of the basis is independent of the choice of coordinates. Therefore, the most straightforward and simple choice, even if one is using spherical coordinates, is the Cartesian triad $\left({{{\rm{e}}_x} = {\partial \over {\partial x}},{{\bf{e}}_y} = {\partial \over {\partial y}},{{\bf{e}}_z} = {\partial \over {\partial z}}} \right)$. With this basis, from a numerical point of view, all tensor components can be regarded as scalars and therefore, a regular tensor can be defined as a tensor field, whose components with respect to this Cartesian frame are expandable in powers of x, y and z (as in Bardeen and Piran [19]). Manipulations and solutions of PDEs for such tensor fields in spherical coordinates are generalizations of the techniques for scalar fields. In particular, when using the multidomain approach with domains having different shapes and coordinates, it is much easier to match Cartesian components of tensor fields. Examples of use of Cartesian components of tensor fields in numerical relativity include the vector Poisson equation [109] or, more generally, the solution of elliptic systems arising in numerical relativity [171]. In the case of the evolution of the unconstrained Einstein system, the use of Cartesian tensor components is the general option, as it is done by the Caltech/Cornell group [127, 188].

The use of an orthonormal spherical basis $\left({{{\rm{e}}_r} = {\partial \over {\partial r}},{{\bf{e}}_\theta} = {1 \over r}{\partial \over {\partial \theta}},{{\bf{e}}_\varphi} = {1 \over {r\sin \theta}}{\partial \over {\partial \varphi}}} \right)$ (see. Figure 19) requires more care. The interested reader can find more details in the work of Bonazzola et al. [44, 37]. Nevertheless, there are systems in general relativity in which spherical components of tensors can be useful:

• When doing excision for the simulation of black holes, the boundary conditions on the excised sphere for elliptic equations (initial data) may be better formulated in terms of spherical components for the shift or the three-metric [62, 104, 123]. In particular, the component that is normal to the excised surface is easily identified with the radial component.

• Still, in the 3+1 approach, the extraction of gravitational radiation in the wave zone is made easier if the perturbation to the metric is expressed in spherical components, because the transverse part is then straightforward to obtain [218].

Problems arise because of the singular nature of the basis itself, in addition to the spherical coordinate singularities. The consequences are first that each component is a multivalued function at the origin r = 0 or on the z-axis, and then that components of a given tensor are not independent from one another, meaning that one cannot, in general, specify each component independently or set it to zero, keeping the tensor field regular. As an example, we consider the gradient Vⁱ = ∇ⁱϕ of the scalar field ϕ = x, where x is the usual first Cartesian coordinate field. This gradient expressed in Cartesian components is a regular vector field V^x = 1, V^y = 0, V^z = 0. The spherical components of V read

$$\begin{array}{*{20}c} {{V^r} = \sin \theta \cos \varphi,}\\ {{V^\theta} = \cos \theta \cos \varphi,}\\ {{V^\varphi} = - \sin \varphi, \quad \;}\\ \end{array}$$

(106)

which are all multidefined at the origin, and the last two on the z-axis. In addition, if V^θ is set to zero, one sees that the resulting vector field is no longer regular: for example the square of its norm is multidefined, which is not a good property for a scalar field. As for the singularities of spherical coordinates, these difficulties can be properly handled with spectral methods, provided that the decomposition bases are carefully chosen.

The other drawback of spherical coordinates is that the usual partial differential operators mix the components. This is due to the nonvanishing connection coefficients associated with the spherical flat metric [37]. For example, the vector Laplace operator (∇_j∇^jVⁱ) reads

$${{{\partial ^2}{V^r}} \over {\partial {r^2}}} + {2 \over r}{{\partial {V^r}} \over {\partial r}} + {1 \over {{r^2}}}\left({{\Delta _{\theta \varphi}}{V^r} - 2{V^r} - 2{{\partial {V^\theta}} \over {\partial \theta}} - 2{{{V^\theta}} \over {\tan \theta}} - {2 \over {\sin \theta}}{{\partial {V^\varphi}} \over {\partial \varphi}}} \right)$$

(107)

$${{{\partial ^2}{V^\theta}} \over {\partial {r^2}}} + {2 \over r}{{\partial {V^\theta}} \over {\partial r}} + {1 \over {{r^2}}}\left({{\Delta _{\theta \varphi}}{V^\theta} + 2{{\partial {V^r}} \over {\partial \theta}} - {{{V^\theta}} \over {{{\sin}^2}\theta}} - 2{{\cos \theta} \over {{{\sin}^2}\theta}}{{\partial {V^\varphi}} \over {\partial \varphi}}} \right)$$

(108)

$${{{\partial ^2}{V^\varphi}} \over {\partial {r^2}}} + {2 \over r}{{\partial {V^\varphi}} \over {\partial r}} + {1 \over {{r^2}}}\left({{\Delta _{\theta \varphi}}{V^\varphi} + {2 \over {\sin \theta}}{{\partial {V^r}} \over {\partial \varphi}} + 2{{\cos \theta} \over {{{\sin}^2}\theta}}{{\partial {V^\theta}} \over {\partial \varphi}} - {{{V^\varphi}} \over {{{\sin}^2}\theta}}} \right),$$

(109)

with Δ_θφ defined in Equation (103). In particular, the r-component (107) of the operator involves the other two components. This can make the resolution of a vector Poisson equation, which naturally arises in the initial data problem [61] of numerical relativity, technically more complicated, and the technique using scalar spherical harmonics (Section 3.2.2) is no longer valid. One possibility can be to use vector, and more generally tensor [146, 239, 218, 51], spherical harmonics as the decomposition basis. Another technique might be to build from the spherical components regular scalar fields, which can have a similar physical relevance to the problem. In the vector case, one can think of the following expressions

$$\Theta = {\nabla _i}{V^i},\quad \chi = {r_i}{V^i},\quad \mu = {r^i}{\epsilon _{ijk}}{\nabla ^j}{V^k},$$

(110)

where r = re_r denotes the position vector and ϵ_ijk the third-rank fully-antisymmetric tensor. These scalars are the divergence, r-component and curl of the vector field. The reader can verify that a Poisson equation for Vⁱ transforms into three equations for these scalars, expandable in terms of scalar spherical harmonics. The reason that these fields may be more interesting than Cartesian components is that they can have more physical or geometric meaning.

3.3 Going further

The development of spectral methods linked with the problems arising in the field of numerical relativity has always been active and continues to be. Among the various directions of research one can foresee, quite interesting ones might be the beginning of higher-dimensional studies and the development of better-adapted mappings and domains, within the spirit of going from pure spectral methods to spectral elements [166, 29].

3.3.1 More than three spatial dimensions

There has been some interest in the numerical study of black holes in higher dimensions, as well as with compactified extra dimensions [202], as in brane world models [199, 132]; recently, some simulations of the head-on collision of two black holes have already been undertaken [230]. With the relatively low number of degrees of freedom per dimension needed, spectral methods should be very efficient in simulations involving four spatial dimensions or more. Here we give starting points to implement four-dimensional (as needed by, e.g., brane world models) spatial representation with spectral methods. The simplest approach is to take Cartesian coordinates (x, y, z, w), but a generalization of spherical coordinates (r, θ, φ, ξ) is also possible and necessitates less computational resources. The additional angle ξ is defined in [0, π] with the following relations with Cartesian coordinates

$$\begin{array}{*{20}c} {x = r\sin \theta \cos \varphi \sin \xi,} \\ {y = r\sin \theta \sin \varphi \sin \xi,} \\ {z = r\cos \theta \sin \xi, \quad \quad}\\ {w = r\cos \xi. \quad \quad \quad \quad}\\ \end{array}$$

(111)

The four-dimensional flat Laplace operator appearing in constraint equations [199] reads

$${\Delta _4}\phi = {{{\partial ^2}\phi} \over {\partial {r^2}}} + {3 \over r}{{\partial \phi} \over {\partial r}} + {1 \over {{r^2}}}\left({{{{\partial ^2}\phi} \over {\partial {\xi ^2}}} + {2 \over {\tan \xi}}{{\partial \phi} \over {\partial \xi}} + {1 \over {{{\sin}^2}\xi}}{\Delta _{\theta \varphi}}\phi} \right),$$

(112)

where Δ_θφ is the two-dimensional angular Laplace operator (103). As in the three-dimensional case, it is convenient to use the eigenfunctions of the angular part, which are here

$$G_k^\ell (\cos \xi)P_\ell ^m(\cos \theta){e^{im\varphi}},$$

(113)

with k, ℓ, m integers such that ∣m∣ ≤ ℓ ≤ k. $P_\ell ^m(x)$ are the associated Legendre functions defined by Equation (100). $G_k^\ell (x)$ are the associated Gegenbauer functions

$$G_k^\ell (\cos \xi) = ({\sin ^\ell}\xi)G_k^{(\ell)}(\cos \xi)\;{\rm{with}}\;G_k^{(\ell)}(x) = {{{d^\ell}{G_k}(x)} \over {d{x^\ell}}},$$

(114)

where G_k(x) is the k-th Gegenbauer polynomial $C_k^{(\lambda)}$ with λ = 1, as the G_k are also a particular case of Jacobi polynomials with a = β = 1/2 (see, for example, [131]). Jacobi polynomials are also solutions of a singular Sturm-Liouville problem, which ensures fast convergence properties (see Section 2.4.1). The G_k(x) fulfill recurrence relations that make them easy to implement as a spectral decomposition basis, like the Legendre polynomials. These eigenfunctions are associated with the eigenvalues −k(k + 2):

$${\Delta _4}(G_k^\ell (\cos \xi)P_\ell ^m(\cos \theta){e^{im\varphi}}) = - k(k + 2)G_k^\ell (\cos \xi)P_\ell ^m(\cos \theta){e^{im\varphi}}.$$

(115)

So, as in 3+1 dimensions, after decomposing in such a basis, the Poisson equation turns into a collection of ODEs in the coordinate r. This type of construction might be generalized to even higher dimensions, with a choice of the appropriate type of Jacobi polynomials for every new introduced angular coordinate.

4 Time-Dependent Problems

From a relativistic point of view, the time coordinate could be treated in the same way as spatial coordinates and one should be able to achieve spectral accuracy for the time representation of a spacetime function f(t, x, y, z) and its derivatives. Unfortunately, this does not seem to be the case and we are neither aware of any efficient algorithm dealing with the time coordinate, nor of any published successful code solving any of the PDEs coming from Einstein’s equations, with the recent exception of the 1+1 dimensional study by Hennig and Ansorg [113]. Why is time playing such a special role? It is not easy to find in the literature on spectral methods a complete and comprehensive study. A first standard explanation is the difficulty, in general, of predicting the exact time interval on which one wants to study the time evolution. In addition, time discretization errors in both finite difference techniques and spectral methods are typically much smaller than spatial ones. Finally, one must keep in mind that, contrary to finite difference techniques, spectral methods store all global information about a function over the whole time interval. Therefore, one reason may be that there are strong memory and CPU limitations to fully three-dimensional simulations; it is already very CPU and memory consuming to describe a complete field depending on 3+1 coordinates, even with fewer degrees of freedom, as is the case for spectral methods. But the strongest limitation is the fact that, in the full 3+1 dimensional case, the matrix representing a differential operator would be very big; it would therefore be very time consuming to invert it in a general case, even with iterative methods.

More details on the standard, finite-difference techniques for time discretization are given in Section 4.1. Due to the technical complexity of a general stability analysis, we restrict the discussion of this section to the eigenvalue stability (Section 4.1) with the following approach: the eigenvalues of spatial operator matrices must fall within the stability region of the time-marching scheme. Although this condition is only a necessary one and, in general, is not sufficient, it provides very useful guidelines for selecting time-integration schemes. A discussion of the imposition of boundary conditions in time-dependent problems is given in Section 4.2. Section 4.3 then details the stability analysis of spatial discretization schemes, with the examples of heat and advection equations, before the details of a fully-discrete analysis are given for a simple case (Section 4.4).

4.1 Time discretization

There have been very few theoretical developments in spectral time discretization, with the exception of Ierley et al. [121], where the authors have applied spectral methods in time to the study of the Korteweg-de Vries and Burger equations, using Fourier series in space and Chebyshev polynomials for the time coordinates. Ierley et al. [121] observe a timestepping restriction: they have to employ multidomain and patching techniques (see Section 2.6) for the time interval, with the size of each subdomain being roughly given by the Courant-Friedrichs-Lewy (CFL) condition. Therefore, the most common approach for time representation are finite-difference techniques, which allow for the use of many well-established time-marching schemes, and the method of lines (for other methods, including fractional stepping, see Fornberg [79]). Let us write the general form of a first-order-in-time linear PDE:

$$\forall t \geq 0,\quad \forall x \in [ - 1,1],\quad {{\partial u(x,t)} \over {\partial t}} = Lu(x,t),$$

(116)

where is a linear operator containing only derivatives with respect to the spatial coordinate x. For every value of time t, the spectral approximation u_N(x, t) is a function of only one spatial dimension belonging to some finite-dimensional subspace of the suitable Hilbert space ${\mathcal H}$, with the given $L_w^2$ spatial norm, associated for example with the scalar product and the weight w introduced in Section 2.3.1. Formally, the solution of Equation (116) can be written as:

$$\forall x \in [ - 1,1],\quad u(x,t) = {e^{Lt}}u(x,0){.}$$

(117)

In practice, to integrate time-dependent problems one can use spectral methods to calculate spatial derivatives and standard finite-difference schemes to advance in time.

4.1.1 Method of lines

At every instant t, one can represent the function u_N(x, t) by a finite set U_N(t), composed of its time-dependent spectral coefficients or its values at the collocation points. We denote L_N the spectral approximation to the operator L, together with the boundary conditions, if the tau or collocation method is used. L_N is, therefore, represented as an N × N matrix. This is the method of lines, which allows one to reduce a PDE to an ODE, after discretization in all but one dimensions. The advantage is that many ODE integration schemes are known (Runge-Kutta, symplectic integrators, …) and can be used here. We shall suppose an equally-spaced grid in time, with the timestep noted Δt and $U_N^J = {U_N}(J \times \Delta t)$.

In order to step from $U_N^J$ to $U_N^{J + 1}$, one has essentially two possibilities: explicit and implicit schemes. In an explicit scheme, the action of the spatial operator L_N on $U_N^K{\vert _{K \leq J}}$ must be computed to explicitly get the new values of the field (either spatial spectral coefficients or values at collocation points). A simple example is the forward Euler method:

$$U_N^{J + 1} = U_N^J + \Delta t{L_N}U_N^J,$$

(118)

which is first order and for which, as for any explicit schemes, the timestep is limited by the CFL condition. The imposition of boundary conditions is discussed in Section 4.2. With an implicit scheme one must solve for a boundary value problem in term of $U_N^{J + 1}$ at each timestep: it can be performed in the same way as for the solution of the elliptic equation (62) presented in Section 2.5.2. The simplest example is the backward Euler method:

$$U_N^{J + 1} = U_N^J + \Delta t{L_N}U_N^{J + 1},$$

(119)

which can be re-written as an equation for the unknown $U_N^{J + 1}$:

$$(I + \Delta t{L_N})U_N^{J + 1} = U_N^J,$$

where I is the identity operator. Both schemes have different stability properties, which can be analyzed as follows. Assuming that L_N can be diagonalized in the sense of the definition given in (4.1.3), the stability study can be reduced to the study of the collection of scalar ODE problems

$${{\partial {U_N}} \over {\partial t}} = {\lambda _i}{U_N},$$

(120)

where λ_i is any of the eigenvalues of L_N in the sense of Equation (124).

4.1.2 Stability

The basic definition of stability for an ODE integration scheme is that, if the timestep is lower than some threshold, then $\Vert U_N^{J + 1}\Vert \leq A{e^{KJ\Delta t}}$, with constants A and K independent of the timestep. This is perhaps not the most appropriate definition, since in practice one often deals with bounded functions and an exponential growth in time would not be acceptable. Therefore, an integration scheme is said to be absolutely stable (or asymptotically stable), if $\Vert U_N^J\Vert$ remains bounded, ∀J ≥ 0. This property depends on a particular value of the product λ_i × Δt. For each time integration scheme, the region of absolute stability is the set of the complex plane containing all the λ_iΔt for which the scheme is absolutely stable.

Finally, a scheme is said to be A-stable if its region of absolute stability contains the half complex plane of numbers with negative real part. It is clear that no explicit scheme can be A-stable due to the CFL condition. It has been shown by Dahlquist [66] that there is no linear multistep method of order higher than two, which is A-stable. Thus implicit methods are also limited in timestep size, if more than second-order accurate. In addition, Dahlquist [66] shows that the most accurate second-order A-stable scheme is the trapezoidal one (also called Crank-Nicolson, or second-order Adams-Moulton scheme)

$$U_N^{J + 1} = U_N^J + {{\Delta t} \over 2}({L_N}U_N^{J + 1} + {L_N}U_N^J).$$

(121)

Figures 20 and 21 display the absolute stability regions for the Adams-Bashforth and Runge-Kutta families of explicit schemes (see, for instance, [56]). For a given type of spatial linear operator, the requirement on the timestep usually comes from the largest (in modulus) eigenvalue of the operator. For example, in the case of the advection equation on [−1, 1], with a Dirichlet boundary condition,

$$\begin{array}{*{20}c} {\quad \quad Lu = {{\partial u} \over {\partial x}},}\\ {\forall t,\quad u(1,t) = 0,}\\ \end{array}$$

(122)

and using a Chebyshev-tau method, one can see that the largest eigenvalue of grows in modulus as N². Therefore, for any of the schemes considered in Figures 20 and 21, the timestep has a restriction of the type

$$\Delta t\underset{\sim}{<} O({N^{- 2}}),$$

(123)

which can be related to the usual CFL condition by the fact that the minimal distance between two points of a (N-point) Chebyshev grid decreases like O(N⁻²). Due to the above mentioned Second Dahlquist barrier [66], implicit time marching schemes of order higher than two also have such a limitation.

Figure 20

Regions of absolute stability for the Adams-Bashforth integration schemes of order one to four.

Figure 21

Regions of absolute stability for the Runge-Kutta integration schemes of order two to five. Note that the size of the region increases with order.

4.1.3 Spectrum of simple spatial operators

An important issue in determining the absolute stability of a time-marching scheme for the solution of a given PDE is the computation of the spectrum (λ_i) of the discretized spatial operator L_N (120). As a matter of fact, these eigenvalues are those of the matrix representation of L_N, together with the necessary boundary conditions for the problem to be well posed (e.g., ${{\mathcal B}_N}u = 0$). If one denotes b the number of such boundary conditions, each eigenvalue λ_i (here, in the case of the tau method) is defined by the existence of a non-null set of coefficients {c_j}_1≤j≤N such that

$$\begin{array}{*{20}c} {(\forall j)1 \leq j \leq N - b,\quad {{({L_N}u)}_j} = {\lambda _i}{c_j},}\\ {\quad \quad \quad \quad \quad \quad \quad \quad {{\mathcal B}_N}u = 0.}\\ \end{array}$$

(124)

As an example, let us consider the case of the advection equation (first-order spatial derivative) with a Dirichlet boundary condition, solved with the Chebyshev-tau method (122). Because of the definition of the problem (124), there are N − 1 “eigenvalues”, which can be computed, after a small transformation, using any standard linear algebra package. For instance, it is possible, making use of the boundary condition, to express the last coefficient as a combination of the other ones

$${c_N} = - \sum\limits_{j = 1}^{N - 1} {{c_j}.}$$

(125)

One is thus left with the usual eigenvalue problem for an (N − 1) × (N − 1) matrix. Results are displayed in Figure 22 for three values of N. Real parts are all negative: the eigenvalue that is not displayed lies on the negative part of the real axis and is much larger in modulus (it is growing as O(N²)) than the N − 1 others.

Figure 22

Eigenvalues of the first derivative-tau operator (124) for Chebyshev polynomials. The largest (in modulus) eigenvalue is not displayed; this one is real, negative and goes as O(N²).

This way of determining the spectrum can be, of course, generalized to any linear spatial operator, for any spectral basis, as well as to the collocation and Galerkin methods. Intuitively from CFL-type limitations, one can see that in the case of the heat equation (Lu = ∂²u/∂x²), explicit time-integration schemes (or any scheme that is not A-stable) will have a severe timestep limitation of the type

$$\Delta t \underset{\sim}{<}O({N^{- 4}}),$$

(126)

for both a Chebyshev or Legendre decomposition basis. Finally, one can decompose a higher-order-in-time PDE into a first-order system and then use one of the above proposed schemes. In the particular case of the wave equation,

$${{{\partial ^2}u} \over {\partial {t^2}}} = {{{\partial ^2}u} \over {\partial {x^2}}},$$

(127)

it is possible to write a second-order Crank-Nicolson scheme directly [157]:

$$U_N^{J + 1} = 2U_N^J - U_N^{J - 1} + {{\Delta {t^2}} \over 2}\left({{{{\partial ^2}U_N^{J + 1}} \over {\partial {x^2}}} + {{{\partial ^2}U_N^{J - 1}} \over {\partial {x^2}}}} \right).$$

(128)

Since this scheme is A-stable, there is no limitation on the timestep Δt, but for explicit or higherorder schemes this limitation would be Δt ≲ O(N⁻²), as for the advection equation. The solution of such an implicit scheme is obtained as that of a boundary value problem at each timestep.

4.1.4 Semi-implicit schemes

It is sometimes possible to use a combination of implicit and explicit schemes to loosen a timestep restriction of the type (123). Let us consider, as an example, the advection equation with nonconstant velocity on [−1, 1],

$${{\partial u} \over {\partial t}} = v(x){{\partial u} \over {\partial x}},$$

(129)

with the relevant boundary conditions, which shall in general depend on the sign of v(x). If, on the one hand, the stability condition for explicit time schemes (123) is too strong, and on the other hand an implicit scheme is too lengthy to implement or to use (because of the nonconstant coefficient υ(x)), then it is interesting to consider the semi-implicit two-step method (see also [94])

$$\begin{array}{*{20}c} {U_N^{J + 1/2} - {{\Delta t} \over 2}L_N^ - U_N^{J + 1/2} = U_N^J + {{\Delta t} \over 2}({L_N} - L_N^ -)U_N^J,\quad \quad \quad}\\ {U_N^{J + 1} - {{\Delta t} \over 2}L_N^ + U_N^{J + 1} = U_N^{J + 1/2} + {{\Delta t} \over 2}({L_N} - L_N^ +)U_N^{J + 1/2},}\\ \end{array}$$

(130)

where $L_N^ +$ and $L_N^ -$ are respectively the spectral approximations to the constant operators −υ(1)∂/∂x and −υ(−1)∂/∂x, together with the relevant boundary conditions (if any). This scheme is absolutely stable if

$$\Delta t \underset{\sim}{<} {1 \over {N\max \vert v(x)\vert}}.$$

(131)

With this type of scheme, the propagation of the wave at the boundary of the interval is treated implicitly, whereas the scheme is still explicit in the interior. The implementation of the implicit part, for which one needs to solve a boundary-value problem, is much easier than for the initial operator (129) because of the presence of only constant-coefficient operators. This technique is quite helpful in the case of more severe timestep restrictions (126), for example for a variable coefficient heat equation.

4.2 Imposition of boundary conditions

The time-dependent PDE (116) can be written as a system of ODEs in time either for the time-dependent spectral coefficients {c_i(t)}_i=0…N of the unknown function u(x, t) (Galerkin or tau methods), or for the time-dependent values at collocation points {u(xi, t)}_i=0…N (collocation method). Implicit time-marching schemes (like the backward Euler scheme (119)) are technically very similar to a succession of boundary-value problems, as for elliptic equations or Equation (62) described in Section 2.5. The coefficients (or the values at collocation points) are determined at each new timestep by inversion of the matrix of type I + ΔtL or its higher-order generalization. To represent a well-posed problem, this matrix needs, in general, the incorporation of boundary conditions, for tau and collocation methods. Galerkin methods are not so useful if the boundary conditions are time dependent: this would require the construction of a new Galerkin basis at each new timestep, which is too complicated and/or time consuming. We shall therefore discuss in the following sections the imposition of boundary conditions for explicit time schemes, with the tau or collocation methods.

4.2.1 Strong enforcement

The standard technique is to enforce the boundary conditions exactly, i.e. up to machine precision. Let us suppose here that the time-dependent PDE (116), which we want to solve, is well posed with boundary condition

$$\forall t \geq 0,\quad u(x = 1,t) = b(t),$$

(132)

where b(t) is a given function. We give here some examples, with the forward Euler scheme (118) for time discretization.

In the collocation method, the values of the approximate solution at (Gauss-Lobatto type) collocation points {xi}_i=0…N are determined by a system of equations:

$$\begin{array}{*{20}c} {\forall i = 0 \ldots N - 1,\quad U_N^{J + 1}({x_i}) = U_N^J({x_i}) + \Delta t({L_N}U_N^J)(x = {x_i}),}\\ {U_N^{J + 1}(x = {x_N} = 1) = b((J + 1)\Delta t),\quad \quad \;\;}\\ \end{array}$$

(133)

where the value at the boundary (x = 1) is directly set to be the boundary condition.

In the tau method, the vector $U_N^J$ is composed of the N + 1 coefficients {c_i(J × Δt)}_i=0…N at the J-th timestep. If we denote by ${({L_N}U_N^J)_i}$ the i-th coefficient of Ln applied to $U_N^J$, then the vector of coefficients {c_i}_i=0…N is advanced in time through the system:

$$\begin{array}{*{20}c} {\forall i = 0 \ldots N - 1,\quad {c_i}((J + 1) \times \Delta t) = {c_i}(J \times \Delta t) + \Delta t{{({L_N}U_N^J)}_i}\quad \quad \quad \quad \quad \quad}\\ {{c_N}((J + 1) \times \Delta t) = b((J + 1)\Delta t) - \sum\limits_{k = 0}^{N - 1} {{c_k},}}\\ \end{array}$$

(134)

the last equality ensures the boundary condition in the coefficient space.

4.2.2 Penalty approach

As shown in the previous examples, the standard technique consists of neglecting the solution to the PDE for one degree of freedom, in configuration or coefficient space, and using this degree of freedom in order to impose the boundary condition. However, it is interesting to try and impose a linear combination of both the PDE and the boundary condition on this last degree of freedom, as is shown by the next simple example. We consider the simple (time-independent) integration over the interval x ∈ [−1, 1]:

$${{{\rm{d}}u} \over {{\rm{d}}x}} = \sin (x - 1),\;{\rm{and}}\;u(1) = 0,$$

(135)

where u(x) is the unknown function. Using a standard Chebyshev relation (161) collocation method (see Section 2.5.3), we look for an approximate solution u_N as a polynomial of degree N verifying

$$\begin{array}{*{20}c} {\forall i = 0 \ldots N - 1,\quad {{{\rm{d}}{u_N}} \over {{\rm{d}}x}}({x_i}) = \sin ({x_i} - 1),}\\ {{{{\rm{d}}{u_N}} \over {{\rm{d}}x}}({x_N} = 1) = 0,}\\ \end{array}$$

where {xi}_i=0…N are the Chebyshev-Gauss-Lobatto collocation points.

We now adopt another procedure that takes into account the differential equation at the boundary as well as the boundary condition, with u_N verifying (remember that x_N = 1):

$$\begin{array}{*{20}c} {\forall i = 0 \ldots N - 1,\quad {{{\rm{d}}{u_N}} \over {{\rm{d}}x}}({x_i}) = \sin ({x_i} - 1),\quad \quad \;}\\ {{{{\rm{d}}{u_N}} \over {{\rm{d}}x}}({x_N}) - \tau {u_N}({x_N}) = \sin ({x_N} - 1),}\\ \end{array}$$

(136)

where τ > 0 is a constant; one notices when taking the limit τ → +∞, that both systems become equivalent. The discrepancy between the numerical and analytical solutions is displayed in Figure 23, as a function of that parameter τ, when using N = 8. It is clear from that figure that there exists a finite value of τ (τ_min ≃ 70) for which the error is minimal and, in particular, lower than the error obtained by the standard technique. Numerical evidence indicates that τ_min ∼ N². This is a simple example of weakly imposed boundary conditions, with a penalty term added to the system. The idea of imposing boundary conditions up to the order of the numerical scheme was first proposed by Funaro and Gottlieb [85] and can be efficiently used for time-dependent problems, as illustrated by the following example. For a more detailed description, we refer the interested reader to the review article by Hesthaven [115].

Let us consider the linear advection equation

$$\forall x \in [ - 1,1],\forall t \geq 0,\quad {{\partial u} \over {\partial t}} = {{\partial u} \over {\partial x}}$$

(137)

$$\forall t \geq 0,\quad u(1,t) = f(t),$$

(138)

where f(t) is a given function. We look for a Legendre collocation method to obtain a solution, and define the polynomial Q−(x), which vanishes on the Legendre-Gauss-Lobatto grid points, except at the boundary x = 1:

$${Q^ -}(x) = {{(1 + x)P_N^\prime(x)} \over {2P_N^\prime(1)}}.$$

Thus, the Legendre collocation penalty method uniquely defines a polynomial u_N(x, t) through its values at Legendre-Gauss-Lobatto collocation points {xi}_i=0…N

$$\forall i = 0 \ldots N,\quad {\left. {{{\partial {u_N}} \over {\partial t}}} \right\vert _{x = {x_i}}} = {\left. {{{\partial {u_N}} \over {\partial x}}} \right\vert _{x = {x_i}}} - \tau {Q^ -}({x_i})({u_N}(1,t) - f(t)),$$

(139)

where τ is a free parameter as in Equation (136). For all the grid points, except the boundary one, this is the same as the standard Legendre collocation method (∀i = 0…N − 1, Q−(xi)=0). At the boundary point x = x_n = 1, one has a linear combination of the advection equation and the boundary condition. Contrary to the case of the simple integration (136), the parameter τ here cannot be too small: in the limit τ → 0, the problem is ill posed and the numerical solution diverges. On the other hand, we still recover the standard (strong) imposition of boundary conditions when τ → +∞. With the requirement that the approximation be asymptotically stable, we get for the discrete energy estimate (see the details of this technique in Section 4.3.2) the requirement

$${1 \over 2}{{\rm{d}} \over {{\rm{d}}t}}{\left\Vert {{u_N}(t)} \right\Vert ^2} = \sum\limits_{i = 0}^N {{u_N}({x_i},t)} {\left. {{{\partial {u_N}} \over {\partial x}}} \right\vert _{x = {x_i}}}{w_i} - \tau u_N^2(t,{x_N}){w_N} \leq 0.$$

Using the property of Gauss00Lobatto quadrature rule (with the Legendre-Gauss-Lobatto weights w_i), and after an integration by parts, the stability is obtained if

$$\tau \geq {1 \over {2{w_N}}} \geq {{N(N + 1)} \over 4}.$$

(140)

It is also possible to treat more complex boundary conditions, as described in Hesthaven and Gottlieb [116] in the case of Robin-type boundary conditions (see Section 2.5.1 for a definition). Specific conditions for the penalty coefficient τ are derived, but the technique is the same: for each boundary, a penalty term is added, which is proportional to the error on the boundary condition at the considered time. Thus, nonlinear boundary operators can also be incorporated easily (see, e.g., the case of the Burgers equation in [115]). The generalization to multidomain solutions is straightforward: each domain is considered as an isolated one, which requires boundary conditions at every timestep. The condition is imposed through the penalty term containing the difference between the junction conditions. This approach has very strong links with the variational method presented in Section 2.6.5 in the case of time-independent problems. A more detailed discussion of the weak imposition of boundary conditions is given in Canuto et al. (Section 3.7 of [57] and Section 5.3 of [58] for multidomain methods).

Figure 23

Behavior of the error in the solution of the differential equation (135), as a function of the parameter τ entering the numerical scheme (136).

4.3 Discretization in space: stability and convergence

After dealing with temporal discretization, we now turn to another fundamental question of numerical analysis of initial value problems, which is to find conditions under which the discrete (spatial) approximation u_N(x, t) converges to the right solution u(x, t) of the PDE (116) as N → ∞ and t ∈ [0, T]. The time derivative term is treated formally, as one would treat a source term on the right-hand side, that we do not consider here, for better clarity.

A given spatial scheme of solving the PDE is said to be convergent if any numerical approximation u_N(x, t), obtained through this scheme, to the solution u(x, t)

$${\left\Vert {{P_N}u - {u_N}} \right\Vert _{L_w^2}} \rightarrow 0\;{\rm{as}}\;N \rightarrow \infty.$$

(141)

Two more concepts are helpful in the convergence analysis of numerical schemes:

• consistency: an approximation to the PDE (116) is consistent if ∀ν ∈ ℌ both

  $$\left. {\begin{array}{*{20}c} {{{\left\Vert {{P_N}(Lv - {L_N}v)} \right\Vert}_{L_w^2}} \rightarrow 0}\\ {{{\left\Vert {{P_N}v - {v_N}} \right\Vert}_{L_w^2}} \rightarrow 0\quad \;\;\;}\\ \end{array}} \right\}\;\;{\rm{as}}\;N \rightarrow \infty;$$

  (142)

• stability: with the formal notations of Equation (117), an approximation to the PDE (116) is stable if

  $$\forall N,\quad \left\Vert {{e^{{L_N}t}}} \right\Vert = \underset{v}{\sup} {{{{\left\Vert {{e^{{L_N}t}}v} \right\Vert}_{L_w^2}}} \over {{{\left\Vert v \right\Vert}_{L_w^2}}}} \leq C(t),$$

  (143)

  where C(t) is independent of N and bounded for t ∈ [0, T].

4.3.1 Lax-Richtmyer theorem

The direct proof of convergence of a given scheme is usually very difficult to obtain. Therefore, a natural approach is to use the Lax-Richtmyer equivalence theorem: “a consistent approximation to a well-posed linear problem is stable if and only if it is convergent”. Thus, the study of convergence of discrete approximations can be reduced to the study of their stability, assuming they are consistent. Hereafter, we sketch out the proof of this equivalence theorem.

The time-evolution PDE (116) is approximated by

$${{\partial {u_N}} \over {\partial t}} = {L_N}{u_{N}}.$$

(144)

To show that stability implies convergence, we subtract it from the exact solution (116)

$${{\partial (u - {u_N})} \over {\partial t}} = {L_N}(u - {u_N}) + Lu - {L_N}u,$$

and obtain, after integration, (the dependence on the space coordinate x is skipped)

$$u(t) - {u_N}(t) = {e^{{L_N}t}}[u(0) - {u_N}(0)] + \int\nolimits_0^t {{e^{{L_N}(t - s)}}[Lu(s) - {L_N}u(s)]{\rm{d}}s.}$$

(145)

Using the stability property (143), the norm ($L_w^2$) of this equation implies

$$\left\Vert {u(t) - {u_N}(t)} \right\Vert \leq C(t)\left\Vert {u(0) - {u_N}(0)} \right\Vert + \int\nolimits_0^t {C(t - s)\left\Vert {Lu(s) - {L_N}u(s)} \right\Vert {\rm{d}}s.}$$

(146)

Since the spatial approximation scheme is consistent and C(t) is a bounded function independent of N, for a given t ∈ [0, T] the left-hand side goes to zero as N → ∞, which proves the convergence.

Conversely, to show that convergence implies stability, we use the triangle inequality to get

$$0 \le\left \vert \left\Vert {{e^{{L_N}t}}u} \right\Vert - \left\Vert {{e^{Lt}}u} \right\Vert \right\vert \leq \left\Vert {{e^{{L_N}t}}u - {e^{Lt}}u} \right\Vert \rightarrow 0.$$

From the well-posedness ∥e^Ltu∥ is bounded and therefore $\Vert {e^{{L_N}t}}u\Vert$ is bounded as well, independent of N.

The simplest stability criterion is the von Neumann stability condition: if we define the adjoint L* of the operator L, using the inner product, with weight w of the Hilbert space

$$\forall (u,v) \in {\mathcal H},\quad {(u,Lv)_w} = {({L^{\ast}}u,v)_w},$$

then the matrix representation $L_N^{\ast}$ of L* is also the adjoint of the matrix representation of L_N. The operator L_N is said to be normal if it commutes with its adjoint $L_N^{\ast}$. The von Neumann stability condition states that, for normal operators, if there exists a constant K independent of N, such that

$$\forall i,1 \leq i \leq N,\quad {{\rm Re}} ({\lambda _i})\; < K,$$

(147)

with (λ_i) being the eigenvalues of the matrix L_N, then the scheme is stable. This condition provides an operational technique for checking the stability of normal approximations. Unfortunately, spectral approximations using orthogonal polynomials have, in general, strongly non-normal matrices L_N and therefore, the von Neumann condition cannot be applied. Some exceptions include Fourier-based spectral approximations for periodic problems.

4.3.2 Energy estimates for stability

The most straightforward technique for establishing the stability of spectral schemes is the energy method: it is based on choosing the approximate solution itself as a test function in the evaluation of residual (60). However, this technique only provides a sufficient condition and, in particular, crude energy estimates indicating that a spectral scheme might be unstable can be very misleading for non-normal evolution operators (see the example in Section 8 of Gottlieb and Orszag [94]).

Some sufficient conditions on the spatial operator L and its approximation L_N are used in the literature to obtain energy estimates and stability criteria, including:

• If the operator L is semibounded:

  $$\exists \gamma, \quad L + {L^{\ast}} \leq \gamma I,$$

  (148)

  where I is the identity operator.

• In the parabolic case, if L satisfies the coercivity condition (see also Chapter 6.5 of Canuto et al. [57]¹):

  $$\exists A > 0,\forall (u,v),\quad \vert(Lu,v)\vert\; \leq A\vert\vert u\vert\vert\vert\vert v\vert\vert,$$

  (149)

  and the continuity condition:

  $$\exists \alpha > 0,\forall u,\quad (Lu,u)\; \leq - \alpha \vert\vert u\vert\vert^{2}.$$

  (150)

• In the hyperbolic case, if there exists a constant C > 0 such that

  $$\forall u,\quad \vert\vert Lu\vert\vert \leq C\vert\vert u\vert\vert,$$

  (151)

  and if the operator verifies the negativity condition:

  $$\forall u,\quad (Lu,u) \leq 0.$$

  (152)

As an illustration, we now consider a Galerkin method applied to the solution of Equation (116), in which the operator L is semibounded, following the definition (148). The discrete solution u_N is such that the residual (60) estimated on the approximate solution u_N itself verifies

$${\left({{{\partial {u_N}} \over {\partial t}} - L{u_N},{u_N}} \right)_w} = 0.$$

(153)

Separating the time derivative and the spatial operator:

$${1 \over 2}{{\rm{d}} \over {{\rm{d}}t}}\left\Vert {{u_N}(t)} \right\Vert _w^2 = {1 \over 2}{((L + {L^{\ast}}){u_N}(t),{u_N}(t))_w},$$

which shows that the “energy”

$${\left\Vert {{u_N}(t)} \right\Vert ^2} \leq {e^{\gamma t}}{\left\Vert {{u_N}(0)} \right\Vert ^2}$$

(154)

grows at most exponentially with time. Since ${u_N}(t) = {e^{{L_N}t}}{u_N}(0)$ for any u_N(0), we obtain

$$\left\Vert {{e^{{L_N}t}}} \right\Vert \leq {e^{{1 \over 2}\gamma t}},$$

(155)

which gives stability and therefore convergence, provided that the approximation is consistent (thanks to the Lax-Richtmyer theorem).

4.3.3 Examples: heat equation and advection equation

4.3.3.1 Heat equation

We first study the linear heat equation

$${{\partial u} \over {\partial t}} - {{{\partial ^2}u} \over {\partial {x^2}}} = 0,\;{\rm{with}}\; - 1 < x < 1,t > 0,$$

(156)

with homogeneous Dirichlet boundary conditions

$$\forall t \geq 0,\quad u(- 1,t) = u(1,t) = 0,$$

(157)

and initial condition

$$\forall - 1 \leq x \leq 1,\quad u(x,0) = {u^0}(x){.}$$

(158)

In the semidiscrete approach, the Chebyshev collocation method for this problem (see Section 2.5.3) can de devised as follows: the spectral solution u_N(t > 0) is a polynomial of degree N on the interval [−1, 1], vanishing at the endpoints. On the other Chebyshev-Gauss-Lobatto collocation points {x_k}_k=1…N−1 (see Section 2.4.3), u_N(t) is defined through the collocation equations

$$\forall k = 1 \ldots N - 1,\quad {{\partial u} \over {\partial t}}({x_k},t) - {{{\partial ^2}u} \over {\partial {x^2}}}({x_k},t) = 0,$$

(159)

which are time ODEs (discussed in Section 4.1) with the initial conditions

$$\forall k = 0 \ldots N,\quad {u_N}({x_k},0) = {u^0}({x_k}){.}$$

(160)

We will now discuss the stability of such a scheme, with the computation of the energy bound to the solution. Multiplying the k-th equation of the system (159) by u_N(x_k, t)w_k, where {w_k}_k=0…N are the discrete weights of the Chebyshev-Gauss-Lobatto quadrature (Section 2.4.3), and summing over k, one gets:

$${1 \over 2}{{\rm{d}} \over {{\rm{d}}t}}\sum\limits_{k = 0}^N {{{({u_N}({x_k},t))}^2}{w_k} -} \sum\limits_{k = 0}^N {{{{\partial ^2}{u_N}} \over {\partial {x^2}}}({x_k},t){u_N}({x_k},t){w_k} = 0{.}}$$

(161)

Boundary points (k = 0, N) have been included in the sum since u_N is zero there due to boundary conditions. The product u_N × ∂²u_N/∂x² is a polynomial of degree 2N − 2, so the quadrature formula is exact

$$\sum\limits_{k = 0}^N {{{{\partial ^2}{u_N}} \over {\partial {x^2}}}({x_k},t){u_N}({x_k},t){w_k} = \int\nolimits_{- 1}^1 {{{{\partial ^2}{u_N}} \over {\partial {x^2}}}({x_k},t){u_N}({x_k},t)w(x){\rm{d}}x,}}$$

(162)

and integrating by parts twice, one gets the relation

$$\int\nolimits_{- 1}^1 {{{{\partial ^2}{u_N}} \over {\partial {x^2}}}({x_k},t){u_N}({x_k},t)w(x){\rm{d}}x = \int\nolimits_{- 1}^1 {{{\left({{{\partial {u_N}} \over {\partial x}}} \right)}^2}w(x){\rm{d}}x - {1 \over 2}\int\nolimits_{- 1}^1 {u_N^2{{{\partial ^2}w} \over {\partial {x^2}}}{\rm{d}}x}}.}$$

(163)

By the properties of the Chebyshev weight

$${{{\partial ^2}w} \over {\partial {x^2}}} - {2 \over w}{\left({{{\partial w} \over {\partial x}}} \right)^2} = 0\;{\rm{and}}\;{{{\partial ^2}w} \over {\partial {x^2}}} = (1 + 2{x^2}){w^5},$$

(164)

it is possible to show that

$$\int\nolimits_{- 1}^1 {u_N^2} {{{\partial ^2}w} \over {\partial {x^2}}}{\rm{d}}x \leq 3\int\nolimits_{- 1}^1 {u_N^2} {w^5}{\rm{d}}x \leq 6\int\nolimits_{- 1}^1 {\;{{{\partial ^2}{u_N}} \over {\partial {x^2}}}} ({x_k},t){u_N}({x_k},t)w(x){\rm{d}}x,$$

(165)

and thus that

$$\int\nolimits_{- 1}^1 {{{{\partial ^2}{u_N}} \over {\partial {x^2}}}({x_k},t){u_N}({x_k},t)w(x){\rm{d}}x \geq {1 \over 4}} \int\nolimits_{- 1}^1 {\;{{\left({{{\partial {u_N}} \over {\partial x}}} \right)}^2}} w(x){\rm{d}}x \geq 0.$$

(166)

Therefore, integrating relation (161) over the time interval [0, t], one obtains

$$\sum\limits_{k = 0}^N {{{({u_N}({x_k},t))}^2}{w_k} \leq \sum\limits_{k = 0}^N {{{({u^0}({x_k}))}^2}{w_k} \leq 2\max \limits_{x \in [0,1]} \vert {u^0}(x){\vert ^2}.}}$$

(167)

The left-hand side represents the discrete norm of u_N(t)², but since this is a polynomial of degree 2N, one cannot apply the Gauss-Lobatto rule. Nevertheless, it has been shown (see, e.g., Section 5.3 of Canuto et al. [57]) that discrete and $L_w^2$-norms are uniformly equivalent, therefore:

$$\int\nolimits_{- 1}^1 {{{({u_N}(x,t))}^2}w(x) \leq 2\max\limits_{x \in [0,1]}} \vert {u^0}(x)\vert ^{2},$$

(168)

which proves the stability of the Chebyshev collocation method for the heat equation. Convergence can again be deduced from the Lax-Richtmyer theorem, but a detailed analysis cf. Section 6.5.1 of Canuto et al. [57]) shows that the numerical solution obtained by the method described here converges to the true solution and one can obtain the convergence rate. If the solution u(x, t) is m-times differentiable with respect to the spatial coordinate x (see Section 2.4.4) the energy norm of the error decays as N^1−m. In particular, if the solution is ${{\mathcal C}^\infty}$, the error decays faster than any power of N.

4.3.3.2 Advection equation

We now study the Legendre-tau approximation to the simple advection equation

$${{\partial u} \over {\partial t}} + {{\partial u} \over {\partial x}} = 0,\;{\rm{with}}\; - 1 < x < 1,t > 0,$$

(169)

with homogeneous Dirichlet boundary condition

$$\forall t \geq 0,\quad u(- 1,t) = 0,$$

(170)

and initial condition

$$\forall - 1 \leq x \leq 1,\quad u(x,0) = {u^0}(x){.}$$

(171)

If we seek the solution as the truncated Legendre series:

$${u_N}(x,t) = \sum\limits_{i = 0}^N {{a_i}(t){P_i}(x)}$$

by the tau method, then u_N satisfies the equation:

$${{\partial {u_N}} \over {\partial t}} + {{\partial {u_N}} \over {\partial x}} = {\tau _N}(t){P_N}(x).$$

(172)

Equating coefficients of P_N on both sides of (172), we get

$${\tau _N} = {{{\rm{d}}{a_N}} \over {{\rm{d}}t}}.$$

Applying the $L_w^2$ scalar product with u_N to both sides of Equation (172), we obtain

$${1 \over 2}{\partial \over {\partial t}}(\vert \vert {u_N}\vert {\vert ^2} - a_N^2) = - \int\nolimits_{- 1}^1 {u{{\partial {u_N}} \over {\partial x}}{\rm{d}}x = - {1 \over 2}u_N^2(1) \leq 0,}$$

which implies the following inequality:

$${{\rm{d}} \over {{\rm{d}}t}}\sum\limits_{i = 0}^{N - 1} {a_i^2 \leq 0.}$$

(173)

Finally, a_N(t) is bounded because it is determined in terms of {a_i}_i=0…N−1 from the boundary condition (170), and thus, stability is proved. In the same way as before, for the heat equation, it is possible to derive a bound for the error ∥u(x, t) − u_N(x, t)∥. if the solution u(x, t) is m-times differentiable with respect to the spatial coordinate x; the energy norm of the error decays like N^1−m (see also Section 6.5.2 of Canuto et al. [57]). In particular, if the solution is ${{\mathcal C}^\infty}$, the error decays faster than any power of N.

4.4 Fully-discrete analysis

Stability issues have been discussed separately for time (Section 4.1.2) and space (Section 4.3) discretizations. The global picture (fully discrete analysis), taking into account both discretizations is, in general, very difficult to study. However, it is possible in some particular cases to address the problem and in the following lines, we shall perform a fully discrete analysis of the advection equation (169), using a Legendre collocation method in space and a forward Euler scheme in time. Using the notation of Section 4.1

$${\left. {\forall x \in [ - 1,1],\quad U_N^{J + 1}(x) = U_N^J(x) - \Delta t{{\partial U_N^J} \over {\partial x}} + \Delta t{{\partial U_N^J} \over {\partial x}}} \right\vert _{x = - 1}}{{{P_{N + 1}}(x)} \over {{P_{N + 1}}(- 1)}},$$

(174)

where the last term imposes the boundary condition ∀J, $U_N^J(x = - 1) = 0$. We consider this relation at the Legendre-Gauss collocation points ({xi}_i=0…N), which are zeros of P_N+₁(x); the square of this expression taken at these collocation points gives

$${\left. {\forall i \in [0,N],\quad {{(U_N^{J + 1}({x_i}))}^2} = {{(U_N^J({x_i}))}^2} + \Delta {t^2}{{\left({{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}}} \right)}^2} - 2\Delta tU_N^J({x_i}){{\partial U_N^J} \over {\partial x}}} \right\vert _{x = {x_i}}}.$$

We multiply by (1 − xi)wi, where {w_i}_i=0…N are the Legendre-Gauss weights, and sum over i to obtain

$$\begin{array}{*{20}c} {\sum\limits_{i = 0}^N {(1 - {x_i}){{\left({U_N^{j + 1}({x_i})} \right)}^2}{w_i} = \sum\limits_{i = 0}^N {(1 - {x_i})} {{\left({U_N^J({x_i})} \right)}^2}} {w_i} - 2\Delta t\sum\limits_{i = 0}^N {(1 - {x_i})U_N^J({x_i}){w_i}{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}}}} \\ {+ \Delta {t^2}\sum\limits_{i = 0}^N {{{\left({{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}}} \right)}^2}(1 - {x_i}){w_i}.}} \\ \end{array}$$

For stability we require that a certain discrete energy of $U_N^J$ be bounded in time:

$$\sum\limits_{i = 0}^N {(1 - {x_i}){{(U_N^{J + 1}({x_i}))}^2}{w_i}} \leq \sum\limits_{i = 0}^N {(1 - {x_i}){{(U_N^J({x_i}))}^2}{w_i},}$$

(175)

which means that

$$\Delta {t^2}\sum\limits_{i = 0}^N {{{\left({{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}}} \right)}^2}(1 - {x_i}){w_i} - 2\Delta t\sum\limits_{i = 0}^N {(1 - {x_i})U_N^J({x_i}){w_i}{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}} \leq 0.} \quad \quad}$$

With the exactness of the Legendre-Gauss quadrature rule for polynomials of degree lower than 2N + 1, we have

$$\sum\limits_{i = 0}^N {{{\left({{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}}} \right)}^2}(1 - {x_i}){w_i} = \int\nolimits_{- 1}^1 {{{\left({{{\partial U_N^J} \over {\partial x}}} \right)}^2}(1 - x){\rm{d}}x,} \quad \quad}$$

and, with an additional integration by parts,

$$\sum\limits_{i = 0}^N {(1 - {x_i})U_N^J({x_i}){w_i}{{\left. {{{\partial U_N^J} \over {\partial x}}} \right\vert}_{x = {x_i}}} = \int\nolimits_{- 1}^1 {(1 - x)U_N^J{{\partial U_N^J} \over {\partial x}}{\rm{d}}x = {1 \over 2}} \int\nolimits_{- 1}^1 {{{(U_N^J(x))}^2}{\rm{d}}x.} \quad}$$

The stability condition obtained from energy analysis translates into an upper bound for the timestep, which can be seen as an accurate estimate of the CFL restriction on the timestep:

$$\Delta t \leq {{\int\nolimits_{- 1}^1 {{{(U_N^J(x))}^2}{\rm{d}}x}} \over {\int\nolimits_{- 1}^1 {{{\left({{{\partial U_N^J} \over {\partial x}}} \right)}^2}(1 - x)\;{\rm{d}}x}}} \simeq {\mathcal O}\left({{1 \over {{N^2}}}} \right).$$

(176)

4.4.1 Strong stability-preserving methods

The above fully-discrete analysis must, in principle, be performed for every time-marching scheme. Therefore, it is very convenient to have a way of extending the results from the first-order Euler method to higher-order methods. Strong stability-preserving Runge-Kutta and multistep methods preserve these kinds of stability properties, including those following from nonlinear stability analysis. A general review of the subject has been done by Shu [200], and we list some results here.

If we consider the general time ODE:

$${{{\rm{d}}{U_N}} \over {{\rm{d}}t}} = {L_N}{U_N},$$

(177)

arising from the spatial discretization of the PDE (116), we suppose that, after discretization in time using the first-order forward Euler scheme, the strong stability requirement $\Vert U_N^{J + 1}\Vert \leq \Vert U_N^J\Vert$ gives a CFL restriction of the type (176)

$$\Delta t \leq \Delta {t_{FE}}.$$

(178)

We can then write an s-stage Runge-Kutta method in the form

$$\begin{array}{*{20}c} {U_N^{(0)} = U_N^J,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ {U_N^{(i)} = \sum\limits_{k = 0}^{i - 1} {\left({{\alpha _{i,k}} + \Delta t{\beta _{i,k}}{L_N}U_N^{(k)}} \right),\;\;\;i = 1, \ldots s,}}\\ {U_N^{J + 1} = U_N^{(s)},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad}\\ \end{array}$$

and see that, as long as α_i,k≥ 0 and β_i,k ≥ 0, all of the intermediate stages are simply convex combinations of forward Euler operators. If this method is strongly stable for L_N, under the condition (178), then the intermediate stages can be bounded and the Runge-Kutta scheme is stable under the CFL condition

$$\Delta t \leq c\Delta {t_{FE}},\quad c = \min\limits_{i,k}{{{\alpha _{i,k}}} \over {{\beta _{i,k}}}}.$$

(179)

In the same manner, one can devise strong stability-preserving explicit multistep methods of the form

$$U_N^{J + 1} = \sum\limits_{i = 1}^s {\left({{\alpha _i}U_N^{J + 1 - i} + \Delta t{\beta _i}{L_N}U_N^{J + 1 - i}} \right),}$$

which can also be cast into convex combinations of forward Euler steps and, therefore, these multistep methods are also stable, provided that

$$\Delta t \leq c\Delta {t_{FE}},\quad c = \min\limits_{i}{{{\alpha _i}} \over {{\beta _i}}}.$$

(180)

Examples of useful coefficients for Runge-Kutta and multistep strong stability-preserving methods can be found in [200, 117]. The best of these methods are those for which the CFL coefficient c is as large as possible.

4.5 Going further: High-order time schemes

When using spectral methods in time-dependent problems, it is sometimes frustrating to have such accurate numerical techniques for the evaluation of spatial derivatives and the integration of elliptic PDEs, while the time derivatives and hyperbolic PDEs do not benefit from spectral convergence. Some tentative studies are being undertaken in order to represent the time interval by spectral methods as well [113]. In their spherically-symmetric study of the wave equation in Minkowski spacetime, Hennig and Ansorg have applied spectral methods to both spatial and time coordinates. Moreover, they have used a conformal compactification of Minkowski spacetime, making the wave equation singular at null infinity. They have obtained nicely accurate and spectrally convergent solutions, even to a nonlinear wave equation. If these techniques can be applied in general three-dimensional simulations, it would really be a great improvement.

Nevertheless, there are other, more sophisticated and accurate time-integration techniques that are currently being investigated for several stiff PDEs [124], including Korteweg-de Vries and nonlinear Schrödinger equations [129]. Many such PDEs share the properties of being stiff (very different time scales/characteristic frequencies) and combining low-order nonlinear terms with higher-order linear terms. Einstein’s evolution equations can also be written in such a way [37]. Let us consider a PDE

$${{\partial u} \over {\partial t}} = Lu + {\mathcal N}u,$$

(181)

using the notation of Section 4.1.1 and ${\mathcal N}$ as a nonlinear spatial operator. Following the same notation and within spectral approximation, one recovers

$${{\partial {U_N}} \over {\partial t}} = {L_N}{U_N} + {{\mathcal N}_N}{U_N}.$$

(182)

We will now describe five methods of solving this type of ODE (see also [124]):

• Implicit-explicit techniques use an explicit multistep scheme to advance the nonlinear part ${{\mathcal N}_N}$, and an implicit one for the linear part.

• Split-step techniques are effective when the equation splits into two equations, which can be directly integrated (see [129] for examples with the nonlinear Schrödinger and Kortewegde Vries equations).

• Integrating factor is a change of variable that allows for the exact solution of the linear part

  $${V_N} = {e^{- {L_N}t}}{U_N},$$

  (183)

  and explicit multistep method for the integration of the new nonlinear part

  $${{\partial {V_N}} \over {\partial t}} = {e^{- {L_N}t}}{{\mathcal N}_N}{e^{{L_N}t}}{V_N}.$$

  (184)

• Sliders can be seen as an extension of the implicit-explicit method described above. In addition to splitting the problem into a linear and nonlinear part, the linear part itself is split into two or three regions (in Fourier space), depending on the wavenumber. Then, different numerical schemes are used for different groups of wavenumbers: implicit schemes for high wavenumbers and explicit high-order methods for low wavenumbers. This method is restricted to Fourier spectral techniques in space.

• Exponential time-differencing techniques have been known for some time in computational electrodynamics. These methods are similar to the integrating factor technique, but one considers the exact equation over one timestep

  $$U_N^{J + 1} = {e^{{L_N}\Delta t}}U_N^J + {e^{{L_N}\Delta t}}\int\nolimits_0^{\Delta t} {{e^{- {L_N}\tau}}{{\mathcal N}_N}({U_N}(N\Delta t + \tau),N\Delta t + \tau)d\tau.}$$

  (185)

  Various orders for these schemes come from the approximation order of the integral. For example Kassam and Trefethen [124] consider a fourth-order Runge-Kutta type approximation to this integral, where the difficulty comes from the accurate computation of functions, that suffer from cancellation errors.

5 Stationary Computations and Initial Data

5.1 Introduction

In this section, we restrict ourselves to problems in which time does not appear explicitly. This is especially the case for systems, that are stationary, like neutron stars in rotation or binary systems in circular orbits. The computation of initial data also falls into this class, given that it consists in finding a particular solution of Einstein’s equations at a given time only. Indeed, when using the standard 3+1 decomposition of spacetime, the initial data that are passed to the evolution equations cannot be totally arbitrary and must satisfy a set of equations called Einstein’s constraint equations. For more details of the initial data problem we refer to the review by Cook [61]. So, in treating the problems considered here, one may forget about the issues specific to time presented in Section 4.

It must be said that spectral methods are not the only technique that has been successfully used to generate stationary spacetimes. [24, 222, 60, 147] give some examples of this, especially in the case of binary systems, for neutron stars or black holes. More references can be found in [61].

5.2 Single compact stars

The computation of the structure of stationary compact stars dates back to 1939 with the famous solution of Tolman-Oppenheimer-Volkoff. During the last few years, the need for accurate models has become more pressing, especially with the coming online of gravitational wave detectors, which could help to probe the interior of such compact stars. Isolated stars in rotation are essentially axisymmetric, but some physical effects can induce a symmetry breaking that could lead to the emission of gravitational waves. In the following, we will review some computations that aim at including some of these effects, such as spontaneous symmetry breaking, the inclusion of magnetic fields, the effects of exotic dense matter (mainly with strange quarks) and the influence of an interior composed of two different superfluids.

5.2.1 Formalisms

The first computation of models of relativistic rotating stars in general relativity, by means of spectral methods, is presented in [41]. The equations are solved in spherical coordinates (see Section 3.2). Doing so, the fields only depend on the azimuthal angle θ and on the radius r. The fields are expanded in terms of spherical harmonics with respect to the angle and in Chebyshev polynomials with respect to r. The use of spherical harmonics is a natural way of dealing with the coordinate singularity on the z-axis. In [41] the whole space is divided into two spherical domains, the outer one extending up to infinity by making use of the compactification in 1/r seen in Section 3.1.2. With such a setting, Einstein’s equations reduce to a set of four elliptic equations with sources extending up to infinity that are solved using a version of the algorithm based on matching with the homogeneous solutions (presented in Section 2.6.4) for each spherical harmonic. The system is complete once a description of the matter is given. The simplest choice is to consider a polytropic fluid, with or without a magnetic field. The system is solved by iteration.

In [41], a particular emphasis is put on various methods to measure the accuracy of the code. For nonrotating stars, the error is found to decrease exponentially, as the number of coefficients increases (see Figures 5 and 6 of [41]). However, for fast-rotating configurations, the error only decays as a power law (see Figure 7 of [41]). This comes from the fact that quantities like the energy density are no longer ${{\mathcal C}^\infty}$ across the star’s surface. Nevertheless, the results are in good agreement (to 0.1%) with those obtained by other numerical methods, as can be seen in [160].

Spectral convergence can be recovered by using surface-adapted coordinates as first done in [36]. A regular mapping of the numerical coordinates to the physical ones is introduced, so that the surface of the star lies at the boundary between two domains (see Section 3.1.1). For polytropes with γ < 2, this is sufficient to recover spectral convergence (see Figures 5 and 6 of [38]). However, for γ > 2, some quantities are still diverging at the surface but the convergence can be made closer and closer to the spectral one by analytically regularizing the density (see Section IV of [38]). Doing so, the error decreases as a power law, but the decrease can be made arbitrary fast at the cost of increasing the number of operations and so the computational time.

Up until 2006, neutron stars were computed using quasi-isotropic coordinates. However, in order to use these configurations as initial data for evolutionary codes, it may be useful to allow for other choices. Among the possible gauges, Dirac’s is one of the most promising [37]. In [134] models of rotating neutron stars in the Dirac gauge are computed for both polytropic and realistic equations of state. Contrary to the quasi-isotropic coordinates, the use of this new gauge implies that one must solve one tensor-like Poisson equation. Configurations obtained with the two different formalisms are shown to be in very good agreement.

5.2.2 Rotating neutron star models

Even before adapted mappings were available, interesting results could be obtained. In [183, 184], models of rotating neutron stars with various equations of state have been computed. Among the most surprising findings is the existence of supra-massive stars. These stars do not connect to the nonrotating limit. Indeed, their high mass can only be supported by the presence of a centrifugal force. One of the remarkable features of such stars is the fact that they actually spin up when they lose angular momentum, contrary to what is observed for normal stars. This effect can also be seen for neutron stars containing hyperons and, thus, a softer equation of state [238]. Let us mention that, in this case, the stability analysis of the configurations required the great precision that spectral methods with adapted coordinates could provide.

It is known that isolated pulsars spin down due to magnetic braking. As the rotational frequency decreases, it is possible that the star will encounter a transition from one state of matter to another. Stationary rotating models have been used to determine the properties of such transitions [231, 232, 233]. A puzzling result is that the amount of energy released in a first-order phase transition does not depend on the orbital velocity of the star and is the same as for nonrotating ones. This is shown to be the case for both weak [232] and strong [233] first-order transitions.

5.2.3 Spontaneous symmetry breaking

It is known that stars can undergo spontaneous symmetry breaking when rotating fast enough. When such a phenomenon occurs, triaxial configurations are formed that are potential emitters of gravitational waves. The departure from axisymmetry is studied in two papers by the Meudon group [34, 35]. The idea of the method is to start from an axisymmetric neutron star configuration and to follow the growth or decay of triaxial instabilities. This work reaffirms well-established results from the Newtonian regime and presents the first results in general relativity for various equations of states. For a few of them, the frequency at which symmetry breaking occurs lies in the frequency band of the LIGO and Virgo detectors.

In 2002, this work was extended [89] by making use of surface-fitting coordinates. This enabled the authors to obtain results in the incompressible case by properly dealing with discontinuities lying at the surface of the star. Classical results in the incompressible case are, thus, recovered and it is found that the inclusion of relativity has only a moderate effect. Indeed, the critical ratio between the kinetic energy and the absolute gravitational energy T/|W| at which the triaxial instability occurs is only 30% larger for relativistic stars, with respect to their classical counterparts.

If relativistic effects only slightly stabilize stars, the same is not true for differential rotation. Indeed, in [182], the authors study various rotation profiles and equations of state using the same technique as in [34, 35] to determine the onset of instability. It appears that the critical value of T/|W| can be almost twice as high as for uniformly rotating stars.

5.2.4 Configurations with magnetic fields

Even if magnetic fields are strong in neutron stars, the structure of the object is not affected until it reaches huge values, on the order of at least 10¹⁰ T. In [32], models of rapidly-rotating stars with poloidal fields are constructed for various equations of state. The magnetic effects are taken into account consistently by solving the appropriate Maxwell equations, as well as by means of spectral methods. The maximum mass of highly-magnetized neutrons stars is found to be higher by 13–29% than for nonmagnetized stars. The magnetic field induces an additional pressure, which can help to support more massive stars, thus explaining this increase.

The presence of a magnetic field can also lead to the deformation of a neutron star. Such deformation could lead to the formation of a triaxial configuration, which would then emit gravitational waves. In [36] the emitted signal is computed. Typically the system radiates at two frequencies: Ω and 2Ω where Ω is the angular velocity of the star.

In more recent work by the Meudon group [159], magnetized configurations have been computed using coordinates matched to the surface of the star, thus making the computation much more accurate. Gyromagnetic ratios of rapidly-rotating neutron stars of various equations of state are obtained. The limit of a ratio of g = 2 value for a charged black hole is never reached.

5.2.5 Strange stars

It is possible that the fundamental state of nuclear matter is not the ordinary matter but rather a plasma of deconfined quarks u, d and s, called strange matter. If this is the case, neutron stars should rather be called strange stars. The main difference between these two types of compact stars is that strange ones are somewhat smaller and thus more compact. In particular, they support higher rotation rates. There is a strong density jump at the surface of a strange star and surface-fitting coordinates are required in order to deal with it.

Fast rotating models of strange stars are computed in [103, 88]. Due to higher compactness, it is found that strange stars can rotate significantly faster than their neutron star counterparts. The attained T/|W| can be twice as large. As in the neutron star case, supermassive configurations that spin up with angular momentum loss are found. The influence of strange matter on the emission of gravitational waves is studied in [90] where viscosity effects and triaxial instabilities are carefully taken into account.

It is believed that millisecond pulsars have been spun up by accreting matter from a companion. However, the details of this mechanism depend on the nature of the compact object. In [237], the differences between accretion onto a neutron star and onto a strange star are investigated, using 2D stationary models computed by spectral methods.

5.2.6 Quasiperiodic oscillations

Quasiperiodic oscillations (QPOs) are observed in the kHz regime and are believed to be the signature of matter falling into a compact object. In the standard picture, the frequency of the QPOs is that of the last stable orbit around the compact object. Let us mention that the presence of a last stable orbit around an extended body is not an effect of relativity but can also be seen in the Newtonian regime, as shown in [234].

The precise structure of the accreting object has a great influence on the QPO. In a series of papers [235, 92, 3, 27], comparisons are made between observations and various compact star models that could account for QPOs.

Using a multidomain approach, strange stars with a crust can also be computed [236], one domain describing the interior of the star and another the crust. It is shown that the presence of the crust could change the value of the QPO by up to 20%.

5.2.7 More complex configurations

In this section, objects in more exotic configurations are presented. This is an illustration of both the complexity of neutron stars physics and the ability of spectral methods to deal with complicated systems.

The observation of glitches in isolated pulsars is consistent with the presence of a superfluid interior. The simplest model considers two fluids, one composed of neutrons and the other of protons and electrons, both components being superfluids. However, these two components could have different velocities, in particular different rotation rates. Such configurations are computed in [177]. A multidomain setting is crucial to be able to follow the two different fluids because the components do not have the same shape. Among the various results obtained, let us mention the confirmation of the existence of prolate-oblate configurations.

Neutron stars are usually assumed to be at zero temperature. However, this approximation is known to no longer be true for newborn neutron stars just after the supernova. Models of newborn neutron stars in uniform rotations are constructed in [106] using an extension of the code developed in [41]. Various hypothesis about the interior (different lepton numbers, isothermal versus isentropic) are considered. Sequences of fixed baryon mass and angular momentum are constructed. Such sequences approximate the evolution of the protoneutron star into a cold neutron star. The results have been extended to differentially-rotating protoneutron stars in [107].

The effect of finite temperature is also investigated in [226]. The authors found that newborn neutron stars are unlikely to undergo bar mode instability, but that the secular ones could take place and result in a significant emission of gravitational waves. Another interesting result of [226] is the existence of toroidal-like configurations, which appear for a broad range of parameters and before the mass-shedding limit. In such cases, the surface of the star is highly deformed and surface-fitting coordinates are required.

Axisymmetric rotating neutron stars have also been computed by a code developed by Ansorg et al. [9, 10]. This code is based on Lewis-Papapetrou coordinates (ρ,ξ), which are closely related to the usual cylindrical coordinates. Typically, space is decomposed into two domains: one for the interior of the star and another for the exterior, which extends up to spatial infinity. Compactification of space and surface-fitting mappings are used. Both variables are expanded in terms of Chebyshev polynomials. Instead of solving the equations harmonic by harmonic and then iterating, as is done by the Meudon group, the equations are written with a collocation method (see Section 2.5.3) and solved as one single system. The price to pay is that the size of the system is somewhat larger (i.e. in m², m being the total number of coefficients for each coordinate). The system is solved by means of the Newton-Raphson method. At each step, the linear system is solved using iterative techniques with preconditioning. With this method, impressive accuracy is reached.

The coordinates used in [9, 10] are more general than the ones used by the Meudon group, especially with respect to their surface-fitting capabilities. They can account for more complicated configurations and, in particular, highly-distorted matter distribution can be obtained. This is shown in [12, 11], where relativistic axisymmetric toroidal configurations of matter, known as the Dyson rings, are computed. Such rings are obtained up to the mass-shedding limit. Transition to the limit of an extreme Kerr black hole is also discussed.

5.3 Single black holes

Compared to the compact star case, single black holes have not been studied very much. This is probably because the structure of a stationary black hole is somewhat simpler than the one of a compact star. However, as will be seen, there are still properties that must be investigated.

Spacetimes containing a single black hole constitute a good benchmark for numerical methods, a lot of results being known analytically. In [125], the authors have implemented a spectral solver and applied it to various test problems. The solver itself is two dimensional and thus applicable only to axisymmetric systems. There is a single domain that consists of the whole space outside a sphere of given radius (i.e. the black hole). Space is compactified by using the standard variable 1/r. The two physical variables (r, θ) are mapped onto squares in ℝ² and then expanded in terms of Chebyshev polynomials. The equations are written using a 2D collocation method (see Section 2.5.3) and the resulting system is solved by an iterative algorithm (here Richardson’s method with preconditioning). This solver is applied to solve Einstein’s constraint equations for three different systems: i) a single black hole ii) a single black hole with angular momentum iii) a black hole plus Brill waves. In all three cases, spectral convergence is achieved and accuracy on the order of 10⁻¹⁰ is reached with 30 points in each dimension.

A black hole is somewhat simpler than a neutron star, in the sense that there is no need for a description of matter (no equation of state, for instance). However, in some formalisms, the presence of a black hole is enforced by imposing a nontrivial solution on a surface (typically a sphere). The basic idea is to demand that the surface be a trapped surface. Such surfaces are known to lie inside event horizons and so are consistent with the presence of a black hole. Discussions about such boundary conditions can be found in [62]. However, in nonstationary cases, the set of equations to be used is not easy to derive. The authors of [123] implement various sets of boundary conditions to investigate their properties. Two different and independent spectral codes are used. Both codes are very close to those used in the case of neutron stars, one of them based on Lorene library [99] (see Section 5.2.1) and the other one developed by Ansorg and sharing a lot a features with [9, 10]. Such numerical tools have proved useful in clarifying the properties of some sets of boundary conditions that could be imposed on black hole horizons.

The reverse problem is also important in the context of numerical relativity. In some cases one needs to know if a given configuration contains a trapped surface and if it can be located at each timestep. Several algorithms have been proposed in the past to find the locus at which the expansion of the outgoing light rays vanishes (thus defining the trapped surface). Even if the term is not used explicitly, the first application of spectral expansions to this problem is detailed in [23]. The various fields are expanded in a basis of symmetric trace-free tensors. The algorithm is applied to spacetimes containing one or two black holes. However, results seem to indicate that high order expansions are required to locate horizons with a sufficient precision.

More recently, another code [135] using spectral methods has been used to locate apparent horizons. It is based on the Lorene library with its standard setting, i.e. a multidomain decomposition of space and spherical coordinates (see Section 5.2.1 for more details). The horizon finder has been successfully tested on known configurations, like Kerr-Schild black holes. The use of spectral methods makes it both fast and accurate. Even if the code uses only one set of spherical coordinates (hence its presentation in this section), it can be applied to situations with more than one black hole, like the well-known Brill-Lindquist data [50].

5.4 Rings around black holes

The problem of uniformly rotating rings surrounding a black hole can be viewed as an intermediate step between one-body axisymmetric configurations and the two body problem. Indeed, even if one has to deal with two components, the problem is still axisymmetric. In [13], configurations of a black hole surrounded by a uniformly rotating ring of matter are computed in general relativity. The matter is assumed to be a perfect fluid. To solve the equations, space is divided into five computational domains. One of them describes the ring itself, another one the region around the black hole and another extends up to infinity. The two other domains are used to connect these regions. One of the difficulties is that the surface of the ring is not know a priori and so the domains must be dynamically adapted to its surface. Cylindrical-type coordinates are used and, in each domain, are mapped onto squares of numerical coordinates. The actual mappings depend on the domain and can be found in Section IV of [13].

Numerical coordinates are expanded in terms of Chebyshev polynomials. The system to be solved is obtained by writing Einstein’s equations in collocation space including regularity conditions on the axis and appropriate boundary conditions on both the horizon of the black hole and at spatial infinity. As in [9, 10], the system is solved iteratively, using the Newton-Raphson method.

Both the Newtonian and relativistic configurations are computed. The ratio between the mass of the black hole and the mass of the ring is varied from zero (no black hole) to 144. The inner mass shedding of the ring can be obtained. One of the most interesting results is the existence of configurations for which the ratio ${J_c}/M_c^2$ of the black hole angular momentum and the square of its mass exceeds one, contrary to what can be achieved for an isolated black hole.

5.5 Compact star binaries

5.5.1 Formalism

Systems consisting of two compact objects are known to emit gravitational waves. Due to this emission, no closed orbits can exist and the objects follow a spiral-like trajectory. This implies that such systems have no symmetries that can be taken into account and full time evolutions should be made. However, when the objects are relatively far apart, the emission of gravitational waves is small and the inspiral slow. In this regime, one can hope to approximate the real trajectory with a sequence of closed orbits. Moreover, the emission of gravitational waves is known to efficiently circularize eccentric orbits so that only circular orbits are usually considered.

So, a lot of effort has been devoted to the computation of circular orbits in general relativity. This can be done by demanding that the system admit a helical Killing vector ∂_t + Ω∂_φ, Ω being the orbital angular velocity of the system. Roughly speaking, this means that advancing in time is equivalent to turning the system around its axis. Working in the corotating frame, one is left with a time-independent problem.

Additional approximations must be made in order to avoid any diverging quantities. Indeed, when using helical symmetry, the system has an infinite lifetime and can fill the whole space with gravitational waves, thus causing quantities like the total mass to be infinite. To deal with that, various techniques can be used, the simplest one consisting of preventing the appearance of any gravitational waves. This is usually done by demanding that the spatial metric be conformally flat. This is not a choice of coordinates but a true approximation that has a priori no reason to be verified. Indeed, even for a single rotating black hole, one can not find coordinates in which the spatial three-metric is conformally flat, so that we do not expect it to be the case for binary systems. However, comparisons with post-Newtonian results or non-conformally-flat results tend to indicate that this approximation is relatively good.

Under these assumptions, Einstein’s equations reduce to a set of five elliptic equations for the lapse, the conformal factor and the shift vector. These equations encompass both the Hamiltonian and momentum constraint equations and the trace of the evolution equations. To close the system, one must provide a description of the matter. It is commonly admitted that the fluid is irrotational, the viscosity in neutron stars being too small to synchronize the motion of the fluid with the orbital motion. It follows that the motion of the fluid is described by an additional elliptic equation for the potential of the flow. The matter terms entering the equations via the stress-energy tensor can then be computed, once an equation of state is given. An evolutionary sequence can be obtained by varying the separation between the stars.

5.5.2 Numerical procedure

Up to now, only the Meudon group has solved these equations by means of spectral methods in the case of two neutron stars. Two sets of domains are used, one centered on each star. Each set consists of sphere-like domains that match the surface of the star and extend up to infinity. Functions are expanded in terms of spherical harmonics with respect to the angles (θ, φ) and Chebyshev polynomials with respect to the radial coordinates. Each Poisson equation ΔN = S_N is split into two parts $\Delta {N_1} = {S_{{N_1}}}$ and $\Delta {N_2} = {S_{{N_2}}}$, such that ${S_N} = {S_{{N_1}}} + {S_{{N_2}}}$ and N = N₁ + N₂. The splitting is, of course, not unique and only requires that ${S_{{N_i}}}$ be mainly centered around star i so that it is well described by spherical coordinates around it. The equation labeled i is then solved using domains centered on the appropriate star. The splittings used for the various equations can be found explicitly in Section IV-C of [100].

The elliptic equations are solved using the standard approach by the Meudon group found in [109]. For each spherical harmonic, the equation is solved using the tau method and the matching between the various domains is made using the homogeneous solutions method (see Section 2.6.4). The whole system of equations is solved by iteration and most of the computational time is spent when quantities are passed from one set of domains to the other by means of a spectral summation (this requires N⁶ operations, N being the number of collocation points in one dimension). A complete and precise description of the overall procedure can be found in [100].

5.5.3 Neutron star binaries

The first sequence of irrotational neutron star binaries computed by spectral means is shown in [40]. Both stars are assumed to be polytropes with an index γ = 2. The results are in good agreement with those obtained simultaneously by other groups with other numerical techniques (see, for instance, [24, 222]). One of the important points that has been clarified by [40] concerns the evolution of the central density of the stars. Indeed, at the end of the 1990s, there was a claim that both stars could individually collapse to black holes before coalescence, due to the increase of central density as the two objects spiral towards each other. Should that have been true, this would have had a great impact on the emitted gravitational wave signal. However, it turned out that this came from a mistake in the computation of one of the matter terms. The correct behavior, confirmed by various groups and in particular by [40], is a decrease in central density as the stars get closer and closer (see Figure I of [40]).

If the first sequence computed by spectral methods is shown in [40], the complete description and validation of the method are given in [100]. Convergence of the results with respect to the number of collocation points is exhibited. Global quantities like the total energy or angular momentum are plotted as a function of the separation and show remarkable agreement with results coming from analytical methods (see Figures 8–15 of [100]). Relativistic configurations are also shown to converge to their Newtonian counterparts when the compactness of the stars is small (see Figures 16–20 of [100]).

Newtonian configurations of compact stars with various equations of state are computed for both equal masses [215] and various mass ratios [212]. One of the main results of the computations concerns the nature of the end point of the sequence. For equal masses, the sequence ends at contact for synchronized binaries and at mass shedding for irrotational configurations. This is to be contrasted with the non-equal-mass case, in which the sequence always ends at the mass shedding limit of the smallest object.

Properties of the sequences in the relativistic regime are discussed in [213, 214]. In [213] sequences with γ = 2 are computed for various compactness and mass ratios for both synchronized and irrotational binaries. The nature of the end point of the sequences is discussed and similar behavior to the Newtonian regime is observed. The existence of a configuration of maximum binding energy is also discussed. Such existence could have observational implications because it could be an indication of the onset of a dynamic instability. Sequences of polytropes with various indexes ranging from 1.8 to 2.2 are discussed in [214]. In particular, the authors are lead to conjecture that, if a configuration of maximum binding energy is observed in the Newtonian regime, it will also be observed in conformal relativity for the same set of parameters.

In [76] the authors derive from the sequences computed in [213] a method to constrain the compactness of the stars from the observations. Indeed, from the results in [213] one can easily determine the energy emitted in gravitational waves per interval of frequency (i.e. the power spectrum of the signal). For large separation, that is, for small frequencies, the curves follow the Newtonian. However, there is a break frequency at the higher end (see Figure 2 of [76]). The location of this frequency depends mainly on the compactness of the stars. More precisely, the more compact the stars are, the higher the break frequency is. Should such frequency be observed by the gravitational wave detectors, this could help to put constraints on the compactness of the neutron stars and, thus, on the equation of state of such objects.

5.5.4 Extensions

The framework of [100] is applied to more realistic neutron stars in [26]. In this work, the equations of state are more realistic than simple polytropes. Indeed, three different equations are considered for the interior, all based on different microscopic models. The crust is also modeled. For all the models, the end point of the evolution seems to be given by the mass shedding limit. However, the frequency at which the shedding occurs depends rather strongly on the EOS. The results are in good agreement with post-Newtonian ones, until hydrodynamic effects begin to be dominant. This occurs at frequencies in the range of 500–1000 Hz, depending on the EOS.

Sequences of strange star binaries have also been computed [133]. Contrary to the neutron star case, matter density does not vanish at the surface of the stars and one really needs to use surface-fitting domains to avoid any Gibbs phenomenon that would spoil the convergence of the overall procedure. Sequences are computed for both synchronized and irrotational binaries and a configuration of maximum binding energy is attained in both cases. This is not surprising: strange stars are more compact than neutron stars and are less likely to be tidally destroyed before reaching the extremum of energy, making it easier to attain dynamic instability. More detailed results on both neutron star and strange star binaries are discussed in [87, 91].

All the work presented above was done in the conformal flatness approximation. As already stated in Section 5.5.1, this is only an approximation and one expects that the true conformal three-metric will depart from flatness. However, in order to maintain asymptotic flatness of space-time, one needs to get rid of the gravitational wave content. One such waveless approximation is presented in [195] and implemented in [223]. Two independent codes are used, one of them being an extension of the work described in [100]. The number of equations to be solved is then greater than in conformal flatness (one has to solve for the conformal metric), but the algorithms are essentially the same. It turns out that the deviation from conformal flatness is rather small. The new configurations are slightly further from post-Newtonian results than the conformally-flat ones, which is rather counter-intuitive and might be linked to a difference in the definition of the waveless approximations.

5.6 Black-hole-binary systems

5.6.1 Digging the holes

Though the computation of black hole binaries in circular orbit has a lot of common features with the neutron star case, there are also some differences that need to be addressed. In at least one aspect, black holes are much simpler objects because they are a solution of Einstein’s equations without matter. So the whole issue of investigating various equations of state is irrelevant and there is no need to solve any equation for the matter. However, there is a price to pay and one must find a way to impose the presence of black holes in the spacetime. Two ideas have been proposed.

In the puncture method, the full spacetime contains three asymptotically-flat regions. One is located at r = ∞ and the other two at two points, M1 an M2, which are called the punctures. The presence of flat regions near the punctures is enforced by demanding that some quantities, like the conformal factor, diverge at those points (typically as 1/r). The discontinuities are taken out analytically and the equations are solved numerically for the regular parts in the whole space. This idea dates back to the work of Brill and Lindquist [50], at least in the case of black holes initially at rest. The puncture approach has been successfully applied to the computation of quasicircular orbits by means of spectral methods in [8].

The apparent horizon method relies on initial works by Misner [150] and Lindquist [140]. In this case, the space has only two asymptotically-flat regions. One can show that this is equivalent to solving Einstein’s equations outside two spheres on which boundary conditions must be imposed. The boundary conditions are based on the concept of trapped surfaces and apparent horizons. The physical state of the black holes are precisely encoded in the boundary conditions.

5.6.2 First configurations

The first configurations of black hole binaries computed by means of spectral methods can be found in [110]. The formalism and various hypotheses are given in the companion paper [98]. The assumptions are very similar to those used for neutron star binaries (see Section 5.5.1). Helical symmetry is enforced and conformal flatness assumed. The holes are described by the apparent horizon technique. However, the boundary conditions used have been shown to be only approximately valid, up to a rather good accuracy. This effect is discussed in the original paper [110] and further explored by Cook in [62]. The numerical techniques are very similar to the ones employed for neutron-star-binary configurations (see Section 5.5.2). Two sets of spherical domains are used, one for each black hole. Boundary conditions are imposed on the surface between the nucleus and the first shell. Both sets extend up to infinity using a compactification in 1/r.

For the first time, good agreement was found between numerical results and post-Newtonian ones. A detailed comparison can be found in [67]. In particular, the location of the energy minimum is shown to coincide to within a few percent. This improvement with respect to previous numerical work is mainly due to a difference in the physical hypothesis (i.e. the use of helical symmetry). One important product of [110] is the use of a new criterion to determine the appropriate value of the orbital angular velocity Ω. Indeed, for neutron stars, this is done by demanding that the fluid of both stars be in equilibrium [100]. This, of course, is not applicable for black holes. Instead, in [98, 110] it is proposed that one find Ω by demanding that the ADM mass and the Komar-like mass coincide. Without going into too much detail, this amounts to demanding that, far from the binary and at first order in 1/r, the metric behave like the Schwarzschild. It is shown in [98] that it can be linked to a relativistic virial theorem. Since then it has been shown that this criterion can also be used for neutron stars [214] and that it is equivalent to the use of a variational principle called the effective potential method [60, 22, 172, 59], where the binding energy is minimized with respect to Ω.

5.6.3 Further investigation

More recently, two other spectral codes have been developed in the context of black hole binaries and successfully applied to address some of the issues raised by the work of [98, 110].

One of these codes comes from the Caltech/Cornell group of Pfeiffer et al. and is described extensively in [171, 167]. The code is multidomain and two main types of domains are used i) square domains in which each Cartesian-like coordinate is expanded in terms of Chebyshev polynomials and ii) spherical domains in which spherical harmonics are used for the angles (θ, φ) and Chebyshev polynomials for the radial coordinate. Space can be compactified by standard use of the variable 1/r. The two types of domains can be set up in various manners to accommodate the desired geometry. When using both square and spherical domains, there are regions of space that belong to more than one domain. This is to be contrasted with work by the Meudon group in which different domains are only touching but not overlapping. The algorithm of [171] solves differential equations by using a multidimensional collocation method. The size of the resulting system is roughly equal to the number of collocation points. It is then solved iteratively via a Newton-Raphson algorithm with a line search. At each step of the Newton-Raphson method, the linear system is solved by means of an iterative scheme (typically GMRES). This inner iterative solver requires careful preconditioning to work properly. Various tests are passed by the code in [171], in which elliptic equations and systems are solved in either spherical or bispherical topologies. In the cases presented, the error decays spectrally.

In [169] the code is used to investigate different ways of solving the constraint equations. Three different decompositions are used: the conformal TT one, the physical TT one and the thin-sandwich decomposition. When solving for the constraint equations only, one must also choose some freely specifiable variables, which describe the physical state of the system. In [169], these specifiable variables are fixed using a superposition of two Kerr-Schild black holes. The net result of [169] is that global quantities, like the total energy, are very sensitive to the choice of decomposition. The variation of total energy can be as large as 5%, which is the order of the energy released by gravitational waves. It is also shown that the choice of extrinsic curvature tensor is more crucial than the one of conformal metric, in accordance with an underlying result of [110]. Let us point out that the equations derived form the helical Killing vector approach in [98, 110] are equivalent to the ones obtained by making use of the thin-sandwich decomposition of the constraints. The freely specifiable variables are obtained by both the imposition of the helical Killing symmetry and by solving an additional equation for the lapse function (resulting in the extended thin-sandwich formalism).

In [63] the boundary conditions based on the apparent horizon formalism [62] are implemented and tested numerically in the case of one and two black holes. In the latter case, the main difference from [110] lies in the use of more elaborate and better boundary conditions on the horizons of the black holes. By allowing for a nonvanishing lapse on the horizons, the authors of [63] solve the constraint equations exactly. This is to be contrasted with [110], where the momentum constraint equation is only solved up to a small correction. Both results show rather good agreement. This is not surprising as the correction used by the Meudon group was known to be small (see Figures 10 and 11 of [110]). More results are presented in [59], for both corotating and irrotational black holes. An important result of [59] is the comparison of the two criteria for determining the orbital angular velocity Ω. They indeed show that the effective potential method first introduced in [60] and the method based on the virial theorem proposed in [98] are in very good agreement.

By slightly extending the boundary conditions used in [59], the authors of [168] propose to reduce the eccentricity of the black-hole-binary configurations. This is done by giving the black holes a small radial velocity by modifying the boundary condition on the shift vector. The code and other equations are the same as in [59]. Time evolution of the obtained initial data does show that this technique can reduce the eccentricity of the binary. However, the effect on the emitted gravitational wave is small and probably unimportant.

Another application of the Caltech/Cornell solver can be found in [143], where the emphasis is put on nearly maximum spinning black holes. Initial data are constructed for both single black holes and binaries. Three families of initial data are investigated. Using a formalism based on the Kerr-Schild spacetime, the authors are able to reach spins as large as a = 0.9998. Such nearly-maximum spinning black holes may be relevant from the astrophysical point of view. Evolutions of these data are also discussed there.

The other spectral code used to compute configurations of black hole binaries comes from Ansorg [6]. It shares a lot of features with the code developed by the same author in the context of rotating stars [9, 10] already discussed in Section 5.2.7. Space is decomposed into two domains. One of them lies just outside the horizons of the black holes and bispherical-like coordinates are used. The other domain extends up to infinity and an appropriate mapping is used in order to avoid the singularity of the bispherical coordinates at spatial infinity (see Section IV of [6]). The angle of the bispherical coordinates (i.e. the angle around the x-axis joining the two black holes) is expanded in terms of a Fourier series and the two other coordinates in terms of Chebyshev polynomials. As in [13, 171], the partial differential equations are solved using a collocation method and the resulting system is solved by the Newton-Raphson method. Once again the linear system coming from the Jacobian is solved by an iterative scheme with preconditioning. The code is used to compute essentially the same configuration as those shown in [59]. An interesting point of [6] is the detailed investigation of the convergence of the results with increased resolution. As can be seen in Figure 4 of [6], the error initially decreases exponentially, but, for high number of points, it seems that the error follows only a power law. This is an indication that some non-${{\mathcal C}^\infty}$ fields must be present. It is conjectured in [6] that this comes from logarithm terms that cannot be dealt with properly with a compactification in 1/r. The same kind of effect is investigated in some detail in [109], where some criteria for the appearance of such terms are discussed.

A code very similar to the one used in [6] has also been used to compute spacetimes with black holes using the puncture approach [8]. Given that the black holes are no longer described by their horizons, one does not need to impose inner boundary conditions. The absence of this requirement enables the author of [8] to use a single domain to describe the whole space, from the puncture up to infinity. The other features of the spectral solver are the same as in [6]. This method has been successfully applied to the computation of black-hole-binary configurations in the puncture framework. The authors have, in particular, investigated high mass ratios between the bodies and compared their results with the ones given in the test-mass limit around a Schwarzschild black hole. The discrepancy is found to be on the order of 50% for the total energy. It is believed that this comes from the fact that the mass of each puncture cannot be directly related to the local black hole mass (see discussion in Section VII of [8]).

Finally, let us mention that the algorithms developed by Ansorg in [9, 10, 8, 6] have all been unified in [7] to accommodate any type of binaries. Various domain decompositions are exhibited that can be used to represent neutron stars, excised black holes or puncture black holes, with the compactification of space. The algorithms are shown to be applicable to limiting cases such as large mass ratios.

5.7 Black-hole-neutron-star binaries

Until recently binaries consisting of a neutron star and a black hole received fewer attention than other types of systems. It was believed, and this was partially true, that this case could easily be handled once the cases of neutron star and black hole binaries were understood. However, such binaries are of evident observational interest and could be the most promising source of gravitational waves for ground-based detectors [28].

The first application of spectral methods to black-hole-neutron-star binaries can be found in [208]. The main approximation is to consider that the black hole is not influenced by the neutron star. Technically, this means that Einstein’s equations are split into two parts (i.e. as for neutron star binaries 5.5.2). However, the part of the fields associated with the black hole is fixed to its analytical value. As the fields are not solved for the black-hole part, the results should depend on the actual splitting, the equations being nonlinear. The part of the fields associated with the neutron star are solved using the standard setting for the Meudon group. Of course, this whole procedure is only valid if the black hole is much more massive than the neutron star and this is why [208] is limited to mass ratios of 10. In this particular case, it is shown that the results depend, to the level of a few percent, on the choice of splitting, which is a measure of the reached accuracy. It is also shown that the state of rotation of the star (i.e. synchronized or irrotational) has little influence on the results.

In [209] the equations of the extended thin-sandwich formulation are solved consistently. As for the neutron-star-binary case, two sets of spherical coordinates are used, one centered around each object. The freely specifiable variables are derived from the Kerr-Schild approach. Configurations are obtained with a moderate mass ratio of five. However, the agreement with post-Newtonian results is not very good and the data seem to be rather noisy (especially the deformation of the star).

Quasiequilibrium configurations based on a helical Killing vector and conformal flatness have been obtained independently by [108] and [210]. Both codes are based on the Lorene library [99] and use two sets of spherical coordinates. They differ mainly in their choice of boundary conditions for the black hole. However, it is shown in the erratum of [108] that the results match pretty well and are in very good agreement with post-Newtonian results. Mass ratios ranging from 1 to 10 are obtained in [210] and the emitted energy spectra are estimated. The work of [210] has been extended in [211], where the parameter space of the binary is extensively explored. In particular, the authors determine whether the end point of the sequences is due to an instability or to the mass-shedding limit. It turns out that the star is more likely to reach the mass-shedding limit if it is less compact and if the mass ratio between the black hole and the star is important, as expected.

More recently, the Caltech/Cornell group has applied the spectral solver of [171, 167] in order to compute black-hole-neutron-star configurations [80]. Some extensions have been made to enable the code to deal with matter by making use of surface-fitting coordinates. Thanks to the domain decomposition used (analogous to the one of [171, 167]), the authors of [80] can reach an estimated accuracy 5 × 10⁻⁵, which is better than the precision of previous works (by roughly an order of magnitude). Configurations with one spinning black hole and configurations with reduced eccentricity are also presented, along the lines of [168].

5.8 Spacetimes with waves

[170] presents a method to produce initial data configurations containing waves. Given a fixed background metric, it shows how to superimpose a given gravitational wave content. The equations are solved numerically using a multidomain spectral code based on [171, 167]. Space is covered by various sphere-like shells and is described up to infinity. When no black hole is present, the origin is covered by a square domain because regularity conditions at the origin, in spherical coordinates, are not handled by [171, 167]. Such a setting is used to generate spacetimes containing i) pure quadrupolar waves ii) flat space with an ingoing pulse and iii) a single black hole superimposed with an ingoing quadrupolar wave.

5.9 Hyperboloidal initial data

If the 3+1 decomposition is the most widely used for numerical relativity, some other possibilities have been proposed, with possibly better features. In particular, one can vary the foliation of spacetime to get hyperboloidal data. With such a setting, at infinity spacetime is foliated by light cones instead of spatial hypersurfaces, which makes the extraction of gravitational waves, in principle, easier.

In [81], Frauendiener is interested in generating hyperboloidal initial-data sets from data in physical space. The technique proceeds in two steps. First a nonlinear partial differential equation (the Yamabe equation) must be solved to determine the appropriate conformal factor ω. Then, the data are constructed by dividing some quantities by this ω. This second step involves an additional difficulty: ω vanishes at infinity but the ratios are finite and smooth. It is demonstrated in [81] that spectral methods can deal with these two steps. Some symmetry is assumed so that the problem reduces to a two-dimensional one. The first variable is periodic and expanded in terms of a Fourier series, whereas Chebyshev polynomials are used for the other. The Yamabe equation is solved using an iterative scheme based on Richardson’s iteration procedure. The construction of the fields, and hence the division by a field vanishing at infinity, is then handled by making use of the nonlocal nature of the spectral expansion (i.e. by working in the coefficient space; see Section 4 of [81] for more details).

6 Dynamic Evolution of Relativistic Systems

The modeling of time-dependent physical systems is traditionally the ultimate goal in numerical simulations. Within the field of numerical relativity, the need for studies of dynamic systems is even more pronounced because of the search for gravitational wave patterns. Unfortunately, as presented in Section 4.1, there is no efficient spectral time discretization yet and one normally uses finite-order time-differentiation schemes. Therefore, in order to get high temporal accuracy, one must use high-order explicit time-marching schemes (e.g., fourth or sixth-order Runge-Kutta [49]). This requires quite a lot of computational power and might explain why, except for gravitational collapse [95, 156], very few studies using spectral methods have dealt with dynamic situations until the Caltech/Cornell group began to use spectral methods in numerical relativity in the early part of this century [128, 127]. This group now has a very well-developed pseudospectral collocation code, “Spectral Einstein Code” (SpEC), for the solution of full three-dimensional dynamic Einstein equations.

In this section, we review the status of numerical simulations that use spectral methods in some fields of general relativity and relativistic astrophysics. Although we may give at the beginning of each section a very short introduction to the context of the relevant numerical simulations, our point is not to give detailed descriptions of them, as dedicated reviews exist for most of the themes presented here and the interested reader should consult them for details of the physics and comparisons with other numerical and analytic techniques. Among the systems that have been studied, one can find gravitational collapse [84] (supernova core collapse or collapse of a neutron star to a black hole), oscillations of relativistic stars [205, 130] and evolution of “vacuum” spacetimes. These include the cases of pure gravitational waves or scalar fields, evolving in the vicinity of a black hole or as (self-gravitating) perturbations of Minkowski flat spacetime. Finally, we will discuss the situation of compact binary [174, 31] spectral numerical simulations.

6.1 Single Stars

The numerical study of the evolution of stars in general relativity involves two parts: first, one must solve for the evolution of matter (relativistic hydrodynamics, see [77]), and second, one must compute the new configuration of the gravitational field. Whereas spectral-methods based codes are now able to study quite well the second part (see Section 6.2), the first has not benefited from the efforts of groups using spectral methods in the past decade. Thus, one faces a paradox: spectral methods have been primarily developed for the simulation of hydrodynamic systems (see Section 1.2), but they are not often used for relativistic hydrodynamics. This might be understood as a consequence of the general problem of spectral methods to deal with discontinuous fields and supersonic flows: the Gibbs phenomenon (see Section 2.4.4). Relativistic flows in astrophysics are often supersonic and therefore contain shocks. Although some techniques have been devised to deal with them in one-dimensional studies (see, e.g., [45]), there has been no convincing multidimensional convincing work. Another problem of multidimensional relativistic hydrodynamics that can spoil rapid convergence properties is sharp density profiles near neutron star surfaces. These can imply a diverging or discontinuous radial derivative of the density, thus slowing down the convergence of the spectral series.

6.1.1 Supernova core collapse

The physical scenario studied here is the formation of a neutron star from the gravitational collapse of a degenerate stellar core. This core can be thought of as the iron core of a massive star at the end of its evolution (standard mechanism of type II supernova). The degeneracy pressure of the electrons can no longer support the gravity and the collapse occurs. When the central density reaches nuclear values, the strong interaction stiffens the equation of state, stopping the collapse in the central region and generating a strong shock. This mechanism has long been thought to be a powerful source of gravitational radiation, but recent simulations show that the efficiency is much lower than previously estimated [70, 195]. The first numerical study of this problem was the spherically-symmetric approach by May and White [148] using artificial viscosity to damp the spurious numerical oscillations caused by the presence of shock waves in the flow solution. Currently, state-of-the-art codes use more sophisticated High-Resolution Shock-Capturing (HRSC) schemes or High-Resolution Central (HRC) schemes (for details on these techniques, see the review by Font [77]). The first axisymmetric fully (general) relativistic simulations of the core collapse scenario were done by Shibata [191] and Shibata and Sekiguchi [195], which used HRSC schemes and a parametric equation of state. More recently, magnetohydrodynamic effects have been taken into account in the axisymmetric core collapse by Shibata et al. [193] using HRC schemes. Three-dimensional core collapse simulations, including a more realistic equation of state and deleptonization scheme have been performed within the cactus-carpet-whisky [217, 17] framework by Ott et al. [164, 163]. These simulations have been compared with those of the Co-CoNuT code (see [68, 69] and later in this section). A more detailed historical presentation can be found in the Living Review by Fryer and New [84].

The appearance of a strong hydrodynamic shock is, in principle, a serious problem to numerical models using spectral methods. Nevertheless, a first preliminary study in spherical symmetry and the Newtonian theory of gravity was undertaken in 1986 by Bonazzola and Marck [43], with the use of “natural” viscosity. The authors show a mass conservation to a level better than 10⁻⁴ using one domain with only 33 Chebyshev polynomials. In 1993, the same authors performed the first three-dimensional simulation (still in Newtonian theory) of the pre-bounce phase [46], giving a computation of the gravitational wave amplitude, which was shown to be lower than standard estimates. Moreover, they showed that for a given mass, the gravitational wave amplitude depends only on the deformation of the core. These three-dimensional simulations were made possible thanks to the use of spectral methods, particularly for the solution of the Poisson equation for the gravitational potential.

Thus, shock waves pose a problem to spectral codes and have either been smoothed with spectral vanishing viscosity [112] or ignored by the code stopping before their appearance. Another idea developed first between the Meudon and Valencia groups was to use more appropriate techniques for the simulation of shock waves: namely the High-Resolution Shock-Capturing techniques, also known as Godunov methods (see the Living Reviews by Martí and Müller [145] and by Font [77]). On the other hand, one wants to keep the fewest degrees of freedom required by spectral methods for an accurate-enough description of functions, in particular for the solution of elliptic equations or for the representation of more regular fields, such as gravitational ones. Indeed, even in the case where a hydrodynamic shock is present, since it only appears as a source for the metric in Einstein’s equations, the resulting gravitational field is at least ${{\mathcal C}^1}$ and the spectral series do converge, although slower than in the smooth case. Moreover, in a multidomain approach, if the shock is contained within only one such domain, it is then necessary to increase resolution in only this particular domain and it is still possible to keep the overall number of coefficients lower than the number of points for the HRSC scheme. The combination of both types of methods (HRSC and spectral) was first achieved in 2000 by Novak and Ibáñez [158]. They studied a spherically-symmetric core collapse in tensor-scalar theory of gravity, which is a more general theory than general relativity and allows a priori for monopolar gravitational waves. The system of PDEs to be solved resembles that of general relativity, with the addition of a scalar nonlinear wave equation for the monopolar dynamic degree of freedom. It was solved by spectral methods, whereas the relativistic hydrodynamics equations were solved by Godunov techniques. Two grids were used, associated to each numerical technique, and interpolations between the two were done at every timestep. Although strong shocks were present in this simulation, they were sharply resolved with HRSC techniques and the gravitational field represented through spectral methods did not exhibit any Gibbs-like oscillations. Monopolar gravitational waveforms could, thus, be given. In collaboration with the Garching relativistic hydrodynamics group, this numerical technique was extended in 2005 to three dimensions, but in the conformally-flat approximation of general relativity (see Sections 5.5 and 5.6) by Dimmelmeier et al. [69]. This approach using spectral methods for the gravitational field computation is now sometimes referred to as the “Marriage des Maillages” (French for “grid wedding”) and is currently employed by the core-collapse code CoCoNuT of Dimmelmeier et al. [68, 69] to study general relativistic simulations of protoneutron stars, with a microphysical equation of state as well as an approximate description of deleptonization [70].

6.1.2 Collapse to a black hole

Stellar collapse to a black hole has been widely studied, starting with spherically-symmetric computations; in the case of dust (matter with no pressure), an analytical solution by Oppenheimer and Snyder [162] was found in 1939. Pioneering numerical works by Nakamura and Sato [153, 154] studied the axisymmetric general relativistic collapse to a black hole; Stark and Piran [203] gave the gravitational wave emission from such a collapse in the formalism of Bardeen and Piran [19]. Fully general relativistic collapse simulations in axisymmetry have also been performed by Shibata [190], and the first three-dimensional calculations of gravitational-wave emission from the collapse of rotating stars to black holes was done by Baiotti et al. [17]. Recently, Stephens et al. [204] developed an evolution code for the coupled Einstein-Maxwell-MHD equations, with application to the collapse to a black hole of a magnetized, differentially-rotating neutron star.

To our knowledge, all studies of the collapse to a black hole, which use spectral methods are currently restricted to spherical symmetry. However, in this case and contrary to the core-collapse scenario, there is a priori no shock wave appearing in the evolution of the system and spectral methods are highly accurate at modeling the hydrodynamics as well. Thus, assuming spherical symmetry, the equations giving the gravitational field are very simple, first because of Birkhoff’s theorem, which gives the gravitational field outside the star, and then from the absence of any dynamic degree of freedom in the gravitational field. For example, when choosing the radial (Schwarzschild) gauge and polar slicing, Einstein’s equations, expressed within 3+1 formalism, turn into two first-order constraints, which are simply solved by integrating with respect to the radial coordinate (see [95]).

In the work of Gourgoulhon [95] a Chebyshev-tau method is used. The evolution equations for the relativistic fluid variables are integrated with a semi-implicit time scheme and a quasi-Lagrangian grid: the boundary of the grid is comoving with the surface of the star, but the grid points remain the usual Gauss-Lobatto collocation points (Section 2.3.2). Due to the singularity-avoiding gauge choice, the collapsing star ends in the “frozen-star” state, with the collapse of the lapse. This induces strong gradients on the metric potentials, but the code is able to follow the collapse down to very small values of the lapse, at less than 10⁻⁶. The code is very accurate at determining whether a star at equilibrium is unstable, by triggering the physical instability from numerical noise at very low level. This property was later used by Gourgoulhon et al. [102] to study the stability of equilibrium configurations of neutron stars near the maximal mass, taking into account the effect of weak interaction processes. The addition of an inward velocity field to the initial equilibrium configurations enabled Gourgoulhon [96] to partially answer the question of the minimal mass of black holes: can the effective mass-energy potential barrier associated with stable equilibrium states be penetrated by stars with substantial inward radial kinetic energy? In [96], Gourgoulhon was able to form a black hole with a starting neutron star that was 10% less massive than the usual maximal mass.

The spectral numerical code developed by Gourgoulhon [95] has been extended to also simulate the propagation of neutrinos, coming from the thermal effect and nonequilibrium weak interaction processes. With this tool, Gourgoulhon and Haensel [101] have simulated the neutrino bursts coming from the collapse of neutron stars, with different equations of state. Another modification of this spectral code has been done by Novak [156], extending the theory of gravity to tensor-scalar theories. This allowed for the simulation of monopolar gravitational waves coming from the spherically-symmetric collapse of a neutron star to a black hole [156]. From a technical point of view, the solution of a nonlinear wave equation on curved spacetime has been added to the numerical model. It uses an implicit second-order Crank-Nicolson scheme for the linear terms and an explicit scheme for the nonlinear part. In addition, as for the hydrodynamics, the wave equation is solved on a grid, partly comoving with the fluid. The evolution of the scalar field shows that the collapsing neutron star has “expelled” all of its scalar charge before the appearance of the black hole.

6.1.3 Relativistic stellar pulsations

Oscillations of relativistic stars are often studied as a time-independent, linear eigenvalue problem [130]. Nevertheless, numerical approaches via time evolutions have proved to bring interesting results, as obtained by Font et al. [78] for the first quasiradial mode frequencies of rapidly-rotating stars in full general relativity. Nonlinear evolution of the gravitational-radiation-driven instability in the r-modes of neutron stars has been studied by many authors (for a presentation of the physical problem, see Section 13 of [5]). In particular, the first study of nonlinear r-modes in rapidly-rotating relativistic stars, via three-dimensional general-relativistic hydrodynamic evolutions has been done by Stergioulas and Font [206]. Different approaches to numerical hydrodynamic simulations in Newtonian gravity have been attempted by Lindblom et al. [139], with an additional braking term, as by Villain and Bonazzola [224] (see the following).

Because of their very high accuracy, spectral methods are able to track dynamic instabilities in the evolution of equilibrium neutron star configurations, as shown in section 6.1.2 by the work of Gourgoulhon et al. [95, 102]. In this work, when the initial data represents a stable neutron star, some oscillations appear, which corresponds to the first fundamental mode of the star. As another illustration of the accuracy, let us mention the work of Novak [155], who followed the dynamic evolution of unstable neutron stars in the tensor-scalar theory of gravity. The instability is linked with the possibility for these stars of undergoing some “spontaneous scalarization”, meaning that they could gain a very high scalar charge, whereas the scalar field would be very weak (or even null) outside the star. Thus, for a given number of baryons, there would be three equilibria for a star: two stable ones with high scalar charges (opposite in sign) and an unstable one with a weak scalar charge. Starting from this last one, the evolution code described in [156] was able to follow the transition to a stable equilibrium, with several hundreds of damped oscillations for the star. This damping is due to the emission of monopolar gravitational waves, which carry away the star’s kinetic energy. The final state corresponds to the equilibrium configuration, independently computed by a simple code solving the generalized Tolman-Oppenheimer-Volkoff system with a scalar field, up to 1% error, after more than 50,000 timesteps. These studies could be undertaken with spectral methods because in these scenarios the flow remains subsonic and one does not expect any shock to be formed.

It is therefore quite natural to try and simulate stellar pulsations using spectral methods. Unfortunately, there have been only a few such studies, which are detailed in the following. Lock-itch et al. [142] have studied the inertial modes of slowly-rotating stars in full general relativity. They wrote down perturbation equations in the form of a system of ordinary differential equations, thanks to a decomposition into vector and tensor spherical harmonics. This system is then a nonlinear eigenvalue problem for the dimensionless mode frequency in the rotating frame. Equilibrium and perturbation variables are then expanded in terms of a basis of Chebyshev polynomials, taking into account the coordinate singularity at the origin and parity requirements. The authors were therefore able to determine the values of the mode frequency, making the whole system singular and looked for eigenfunctions, through their spectral decomposition. They found that inertial modes were slightly stabilized by relativistic effects.

A different and maybe more natural approach, namely the time integration of the evolution equations, has been undertaken by Villain et al. [224, 225] with a spectral magnetohydrodynamics code in spherical coordinates. The code solves the linearized Euler or Navier-Stokes equations, with the anelastic approximation. This approximation, which is widely used in other fields of astrophysics and atmospheric physics, consists in neglecting acoustic waves by assuming that time derivatives of the pressure and the density perturbations are negligible. It allows for a characteristic time, which is not set by acoustic propagation time, but is much longer and the timestep can be chosen so as to follow the inertial modes themselves. In their 2002 paper [224], Villain et al. study inertial modes (i.e. modes whose restoring force is the Coriolis force, among which the r-modes [5]) in slowly rotating polytropes with γ = 2 in the linear regime. First, this is done in the framework of Newtonian gravity, where the anelastic approximation implies that the Eulerian perturbations of the gravitational potential do not play any role in the velocity perturbations. Second, they study the relativistic case, but with the Cowling approximation, meaning again that the metric perturbations are discarded. In both regimes and trying different boundary conditions for the velocity field at the surface of the star, they note the appearance of a polar part of the mode and the “concentration of the motion” near the surface, showing up in less than 15 periods of the linear r-mode. A more recent work [225] deals with the study of gravity modes, in addition to inertial modes, in neutron stars. The interesting point of this work is the use of a quite realistic equation of state for nuclear matter, which is valid even when beta equilibrium is broken. The authors were, thus, able to show that the coupling between polar and axial modes is increasing with the rotation of the star, and that the coupling of inertial modes with gravity modes in nonbarotropic stars can produce fast energy exchanges between polar and axial parts of the fluid motion. From a numerical point of view, one of the key ingredients is the solution of the vector heat equation, coming from the Euler or Navier-Stokes equations. This is done by a poloidal-toroidal [47] decomposition of the velocity field into two scalar potentials, which is very natural in spectral methods. Moreover, to ensure correct analytical behavior at the origin, all scalar quantities are projected at each timestep to a modified Legendre function basis.

More recently, a complete nonlinear study of rotating star pulsations has been set by Dimmelmeier et al. [71]. They used the general relativistic code CoCoNuT (see above, Section 6.1.1) in axial symmetry, with an HRSC hydrodynamic solver, and spectral methods for the simplified Einstein equations (conformally-flat three metric). They noted that the conformal flatness condition did not have much effect on the dynamics when comparing with the Cowling approximation. Nevertheless, they found that differential rotation was shifting the modes to lower frequencies and they confirmed the existence of the mass-shedding-induced damping of pulsations.

6.2 Vacuum and black hole evolutions

If one wants to simulate the most interesting astrophysical sources of gravitational radiation, one must have a code able to follow, in a stable manner, gravitational waves themselves on a background spacetime. It has been observed by all numerical relativity groups that the stability of a numerical code, which solves Einstein’s field equations, not only depends on the numerical algorithm, but also on the particular formulation of the equations. Successes in the simulations of binary systems of compact objects in general relativity (see Section 6.3) are also due to numerous studies and advances in the formulations of Einstein’s equations. The methods known at present that work for the numerical evolution of binaries are the generalized harmonic coordinate method [82, 86, 176] and the BSSN method (for Baumgarte-Shapiro-Shibata-Nakamura [25, 194]). In particular, these two formulations of the field equations have the important property that constraint violating modes (see discussion following) stay at a reasonable level during the evolution. Use of the generalized harmonic gauge requires constraint damping terms; and a particular method suited for harmonic evolution, which was proposed by Gundlach et al. [111], enabled Pretorius to evolve black hole spacetimes [176, 175].

It is, therefore, a crucial step to devise such a stable formulation, and more particularly with spectral methods, because they add very little numerical dissipation and thus, even the smallest instability is not dissipated away and can grow to an unacceptable level. The situation becomes even more complicated with the setup of an artificial numerical boundary at a finite distance from the source, needing appropriate boundary conditions to control the physical wave content, and possibly to limit the growth of unstable modes. All these points have been extensively studied since 2000 by the Caltech/Cornell groups and their pseudospectral collocation code SpEC [125, 127, 187, 186, 138, 120, 126, 137, 49]; they were followed in 2004 by the Meudon group [37] and in 2006 by Tichy [219].

Next, it is necessary to be able to evolve black holes. Successful simulations of black hole binaries have been performed using the black-hole puncture technique [55, 18]. Unfortunately, the dynamic part of Einstein fields are not regular at the puncture points and it seems difficult to regularize them so as to avoid any Gibbs-like phenomenon using spectral methods. Therefore, punctures are not generally used for spectral implementations; instead the excision technique is employed, removing part of the coordinate space inside the apparent horizon. There is no need for boundary conditions on this new artificial boundary, provided that one uses a free-evolution scheme [187], solving only hyperbolic equations. In the considered scheme, and for hydrodynamic equations as well, one does not need to impose any boundary condition, nor do any special treatment on the excision boundary, contrary to finite difference techniques, where one must construct special onesided differencing stencils. On the other hand, with a constrained scheme, elliptic-type equations are to be solved [37] and, as for initial data (see Sections 5.3 and 5.6), boundary conditions must be provided, e.g., on the apparent horizon, from the dynamic horizon formalism [105].

Finally, good outer boundary conditions, which are at the same time mathematically well posed, consistent with the constraints and prevent as much as possible reflections of outgoing waves, must be devised. In that respect, quite complete boundary conditions have been obtained by Buchman and Sarbach [53].

6.2.1 Formulation and boundary conditions

Several formulations have been proposed in the literature for the numerical solution of Einstein’s equations using spectral methods. The standard one is the 3+1 (a.k.a. Arnowitt-Deser-Misner-ADM) formalism of general relativity [14, 229] (for a comprehensive introduction, see the lecture notes by Gourgoulhon [97]), which has been reformulated into the BSSN [25, 194] for better stability. But first, let us mention an alternative characteristic approach based on expanding null hypersurfaces foliated by metric two-spheres developed by Bartnik [20]. This formalism allows for a simple analysis of the characteristic structure of the equations and uses the standard “edth” (ð) operator on S² to express angular derivatives. Therefore, Bartnik and Norton [21] use spin-weighted spherical harmonics (see Section 3.2.2) to numerically describe metric fields.

Coming back to the 3+1 formalism, Einstein’s equations split into two subsets of equations. First, the dynamic equations specifying the way the gravitational field evolves from one timeslice to the next; then, the constraint equations, which must be fulfilled on each timeslice. Still, it is well known that for the Einstein system, as well as for Maxwell’s equations of electromagnetism, if the constraints are verified on the initial timeslice, then the dynamic equations guarantee that they shall be verified in the future of that timeslice. Unfortunately, when numerically doing such free evolution, i.e. solving only for the dynamic equations, small violations of the constraints due to round-off errors appear to grow exponentially (for an illustration with spectral methods, see, e.g., [187, 219]). The opposite strategy is to discard some of the evolution equations, keeping the equations for the two physical dynamic degrees of freedom of the gravitational field, and to solve for the four constraint equations: this is a constrained evolution [37].

The advantages of the free evolution schemes are that they usually allow one to write Einstein’s equations in the form of a strongly- or symmetric-hyperbolic system, for which there are many mathematical theorems of existence and well-posedness. In addition, it is possible to analyze such systems in terms of characteristics, which can give very clear and easy-to-implement boundary conditions [126]. Using finite-difference numerical methods, it is also very CPU-time consuming to solve for constraint equations, which are elliptic in type, but this is not the case with spectral methods. On the other hand, constrained evolution schemes have, by definition, the advantage of not being subject to constraint-violation modes. Besides, the equations describing stationary spacetimes are usually elliptic and are naturally recovered when taking the steady-state limit of such schemes. Finally, elliptic PDEs usually do not exhibit instabilities and are known to be well posed. To be more precise, constrained evolution using spectral methods has been implemented by the Meudon group [37], within the framework of the BSSN formulation. Free-evolution schemes have been used by Tichy [219] (with the BSSN formulation) and by the Caltech/Cornell group, which has developed their Kidder-Scheel-Teukolsky (KST) scheme [127] and have later used the Generalized-Harmonic (GH) scheme [137]. The KST scheme is, in fact, a 12-parameter family of hyperbolic formulations of Einstein’s equations, which can be fine tuned in order to stabilize the evolution of, e.g., black hole spacetimes [187].

Even when doing so, constraint-violating modes grow exponentially and three ways of controlling their growth have been studied by the Caltech/Cornell group. First, the addition of multiples of the constraints to the evolution system in order to minimize this growth. The parameters linked with these additional terms are then adjusted to control the evolution of the constraint norm. This generalized version of the dynamic constraint control method used by Tiglio et al. [221] has been presented by Lindblom et al. [138] and tested on a particular representation of the Maxwell equations. Second, Lindblom et al. [138] devised constraint preserving boundary conditions from those of Calabrese et al. [54], where the idea was to get maximally dissipative boundary conditions on the constraint evolution equations [138, 126]. This second option appeared to be more efficient, but still did not completely eliminate the instabilities. Finally, bulk constraint violations cannot be controlled by constraint-preserving boundary conditions alone, so Holst et al. [120] derived techniques to project at each timestep the solution of the dynamic equations onto the constraint submani-fold of solutions. This method necessitates the solution of a covariant inhomogeneous Helmholtz equation to determine the optimal projection. Nevertheless, the most efficient technique seems to be the use of the GH formulation, which also incorporates multiples of the constraints, thus exponentially suppressing bulk constraint violation, together with constraint-preserving boundary conditions [137].

Boundary conditions are not only important for the control of the constraint-violation modes in free evolutions. Because they cannot be imposed at spatial infinity (see Section 3.1.2), they must be completely transparent to gravitational waves and prevent any physical wave from entering the computational domain. A first study of interest for numerical relativity was done by Novak and Bonazzola [157], in which gravitational waves are considered in the wave zone, as perturbations of flat spacetime. The specificity of gravitational waves is that they start at the quadrupole level (ℓ = 2) in terms of spherical harmonics expansion. Standard radiative boundary conditions (known as Sommerfeld boundary conditions [201]) being accurate only for the ℓ = 0 component, a generalization of these boundary conditions has been done to include quadrupolar terms [157]. They strongly rely on the spectral decomposition of the radiative field in terms of spherical harmonics and on spherical coordinates. More specific boundary conditions for the Einstein system, in order to control the influx of the radiative part of the Weyl tensor, have been devised by Kidder et al. [126] for the KST formulation, generalizing earlier work by Stewart [207] and Calabrese et al. [54]. They were then adapted to the GH formulation by Lindblom et al. [137]. Rinne [179] has studied the well-posedness of the initial-boundary-value problem of the GH formulation of Einstein’s equations. He has considered first-order boundary conditions, which essentially control the incoming gravitational radiation through the incoming fields of the Weyl tensor. He has also tested the stability of the whole system with a collocation pseudospectral code simulating a Minkowski or Schwarzschild perturbed spacetime. Generalizing previous works, a hierarchy of absorbing boundary conditions has been introduced by Buchman and Sarbach [53], which have then been implemented in the Caltech/Cornell SpEC code by Ruiz et al. [181], together with new sets of absorbing and constraint-preserving conditions in the generalized harmonic gauge. Ruiz et al. have shown that their second-order conditions can control the incoming gravitational radiation, up to a certain point. In addition, they have analyzed the well-posedness of the initial-boundary-value problems arising from these boundary conditions. Rinne et al. [180] have compared various methods for treating outer boundary conditions. They have used the SpEC code to estimate the reflections caused by the artificial boundary, as well as the constraint violation it can generate.

6.2.2 Gauges and wave evolution

The final ingredient before performing a numerical simulation of the dynamic Einstein system is the gauge choice. For example, the analytical study of the linearized gravitational wave in vacuum has been done with the harmonic gauge, for which the coordinates {x^μ} verify the scalar covariant wave equation

$${H_\mu} = {g_{\mu \nu}}{\nabla _\sigma}{\nabla ^\sigma}{x^\nu} = 0.$$

(186)

This is the definition of the form H_μ, where g_μν is the metric and ∇_σ the associated covariant derivative. Recent work by the Caltech/Cornell group uses the GH formulation in which the gauge choice is achieved through the specification of H_μ as an arbitrary function of {x^μ} and g_μν, which can be set, for instance, to its initial value [188]. Still, it is with the KST formulation, and with the lapse and shift set from the analytic values, that Boyle et al. [49] have submitted the Caltech/Cornell SpEC code to the “Mexico City tests” [2]. These are a series of basic numerical relativity code tests to verify their accuracy and stability, including small amplitude linear plane wave, gauge wave and Gowdy spacetime evolutions. These tests have been passed by the Caltech-Cornell code using a Fourier basis for all three Cartesian coordinates and a fourth-order Runge-Kutta timestep-ping scheme. In the particular case of the linear plane wave, Boyle et al. [49] exhibit the proper error behavior, which increases as the square of the wave amplitude, because all nonlinear terms are neglected in this test. The authors have also shown that the use of filtering of the spherical harmonics coefficients was very effective in reducing nonlinear aliasing instabilities. Gauge drivers for the GH formulation of Einstein’s equations have been devised by Lindblom et al. [136]. They provide an elegant way of imposing gauge conditions that preserve hyperbolicity for many standard gauge conditions. These drivers have been tested with the SpEC code.

Within the constrained formulation of Einstein’s equations, the Meudon group has introduced a generalization of the Dirac gauge to any type of spatial coordinates [37]. Considering the conformal 3+1 decomposition of Einstein’s equations, the Dirac gauge requires that the conformal three-metric ${{\tilde \gamma}^{ij}}$ (such that det ${{\tilde \gamma}^{ij}} = 1$) be divergence-free with respect to the flat three-metric (defined as the asymptotic structure of the three-metric and with the associated covariant derivative ${\bar D}$)

$${\bar D_i}{\tilde \gamma ^{ij}} = 0.$$

(187)

The time coordinate is set by the standard maximal slicing condition. These conditions turn out to be dynamic gauge conditions: the lapse and the shift are determined through the solution of elliptic PDEs at each timestep. With this setting, Bonazzola et al. have studied the propagation of a three-dimensional gravitational wave, i.e. the solution of the fully nonlinear Einstein equations in vacuum. Their multidomain spectral code based on the Lorene library [99] was able to follow the wave using spherical coordinates, including the (coordinate) singular origin, and to let it out of the numerical grid with transparent boundary conditions [157]. Evolution was performed with a second-order semi-implicit Crank-Nicolson time scheme, and the elliptic system of constraint equations was solved iteratively. Since only two evolution equations were solved (out of six), the others were used as error indicators and proved the awaited second-order time convergence. A preliminary analysis of the mathematical structure of the evolution part of this formalism done by Cordero et al. [64] has shown that the choice of Dirac’s gauge for the spatial coordinates guarantees the strongly hyperbolic character of that system as a system of conservation laws.

6.2.3 Black hole spacetimes

As stated at the beginning of Section 6.2, the detailed strategy to perform numerical simulations of black hole spacetimes depends on the chosen formulation. With the characteristic approach, Bartnik and Norton [21] modeled gravitational waves propagating on a black hole spacetime in spherical coordinates, but with a null coordinate z = t − r. Interestingly, they combined a spectral decomposition on spin-weighted spherical harmonics for the angular coordinates and an eighth-order scheme using spline convolution to calculate derivatives in the r or z direction. Integration in these directions was done with a fourth or eighth-order Runge-Kutta method. For the spectral part, they had to use Orszag’s 2/3 rule [56] for antialiasing. This code achieved a global accuracy of 10⁻⁵ and was able to evolve the black hole spacetime up to z = 55 M. More recently, Tichy has evolved a Schwarzschild black hole in Kerr-Schild coordinates in the BSSN formulation, up to t ≃ 100 M [219]. He used spherical coordinates in a shell-like domain, excising the interior of the black hole. The expansion functions are Chebyshev polynomials for the radial direction, and Fourier series for the angular ones.

Most successful simulations in this domain have been performed by the Caltech/Cornell group, who seem to be able to stably evolve forever not only a Schwarzschild, but also a Kerr black hole perturbed by a gravitational wave pulse [137], using their GH formulation with constraint-damping and constraint-preserving boundary conditions. However, several attempts had been reported by this group before, starting with the spherically-symmetric evolution of a Schwarzschild black hole by Kidder et al. [128]. Problems had arisen when trying three-dimensional simulations of such physical systems with the new parameterized KST formalism [127]. Using spherical coordinates in a shell-like domain, the authors decomposed the fields (or Cartesian components for tensor fields) on a Chebyshev radial base and scalar spherical harmonics. The integration in time was done using a fourth-order Runge-Kutta scheme and the gauge variables were assumed to keep their analytical initial values. The evolution was limited by the growth of constraint-violating modes at t ∼ 1000 M. With a fine-tuning of the parameters of the KST scheme, Scheel et al. [187] have been able to extend the lifetime of the numerical simulations to about 8000 M. On the other hand, when studying the behavior of a dynamic scalar field on a fixed Kerr background, Scheel et al. [186] managed to get nice results on the late time decay of this scalar field. They had to eliminate high-frequency numerical instabilities, with a filter on the spherical harmonics basis, following again Orszag’s 2/3 rule [56] and truncating the last third of the coefficients. It is interesting to note that no filtering was necessary on the radial (Chebyshev) basis functions. A more complicated filtering rule has been applied by Kidder et al. [126] when trying to limit the growth of constraint-violation in three-dimensional numerical evolutions of black hole spacetimes with appropriate boundary conditions. They have set to zero the spherical harmonics terms with ℓ ≥ ℓ_max − 3 in the tensor spherical harmonics expansion of the dynamic fields. The stable evolutions reported by Lindblom et al. [137], thus, might be due to the following three ingredients:

• GH formalism, exponentially suppressing all small short-wavelength constraint violations,

• constraint-preserving boundary conditions,

• the filtering of spherical harmonics spectral coefficients.

6.3 Binary systems

As seen in Section 6.2, not many groups using spectral methods are able to solve all the three-dimensional Einstein equations in a stable way. When dealing with black holes, the situation is even worse. Only very recently, the Caltech/Cornell group succeeded in following 16 orbits, merger and ring-down of an equal-mass nonspinning black-hole-binary system [185]. Moreover, we can report on three recent partial results in the field using spectral methods, dealing with each type of binary system (neutron stars and/or black holes) and leaving space for future study in this rapidly evolving field. We note, of course, that successful numerical evolutions of such systems have been performed with other numerical methods, which we very briefly summarize here. The first successful fully-relativistic simulation of neutron star binaries was obtained by Shibata et al. [196, 192] and now, more groups are also able to study such systems: the Louisiana State University (LSU) group [4] and the Albert Einstein Institute (AEI, Golm) group [16]. We should also mention here the more microphysically-detailed simulations by Oechslin and Janka [161], although with the conformally-flat approximation, and those of Liu et al. [141] evolving magnetized neutron star binaries. Shibata and Uryū [197, 198] have successfully evolved black-hole-neutron-star binaries using the puncture technique for the modeling of the black hole. As far as black hole binary systems are concerned, after many years of hard work and codes evolving the binary system for a restricted time, a first stable simulation up to the merger phase has been performed by Pretorius [175], who used general harmonic coordinates together with constraint-damping terms and a compactification of spatial infinity. He also used the excision technique for a region surrounding the singularity inside the horizon. This first success was followed a few moths later by the Texas/Brownsville group [55] and the NASA/Goddard group [18], using very different techniques, namely BSSN with moving punctures and “1+log” slicing together with a “Γ-driver” shift condition. These techniques have rapidly become standards for many other groups, which are now able to stably evolve black hole binaries, such as the AEI/LSU collaboration [173], the group in Jena [93], that at Pennsylvania State University [114] and at Florida Atlantic University [220]. The results have reached a high level of confidence and it is possible to compare gravitational waveforms obtained from numerical evolution with post-Newtonian template families [165].

6.3.1 Neutron star binaries

Numerical simulations of the final stage of inspiral and merger of neutron star binaries have been performed by Faber et al. [75], who used spectral methods in spherical coordinates (based on Lorene library [99]) to solve Einstein’s equations in the conformally-flat approximation (see Sections 5 and 6.1.1). The hydrodynamic evolution has been computed using a Lagrangian smoothed particle hydrodynamics (SPH) code. As for the initial conditions described in Section 5.5, the equations for the gravitational field reduce, in the case of the conformally-flat approximation, to a set of five nonlinear coupled elliptic (Poisson-type) PDEs. The considered fields (lapse, shift and conformal factor) are “split” into two parts, each component being associated with one of the stars in the binary. Although this splitting is not unique, the result obtained is independent from it, because the equations with the complete fields are solved iteratively, for each timestep. Boundary conditions are imposed on each solution of the field equations at radial infinity thanks to a multidomain decomposition and a u = 1/r compactification in the last domain. The authors used ∼ 10⁵ SPH particles for each run, with an estimated accuracy level of 1–2%. Most of the CPU time was spent in calculating the values of quantities known from their spectral representation, at SPH particle positions. Another difficulty has been the determination of the domain boundary containing each neutron star, avoiding any Gibbs phenomena. Because the conformally-flat approximation discards gravitational waves, the dissipative effects of gravitational radiation back reaction were added by hand. The authors used the slow-motion approximation [227] to induce a shrinking of the binary systems, and the gravitational waves were calculated with the lowest-order quadrupole formulae. The code has passed many tests and, in particular, it has evolved several quasiequilibrium binary configurations without adding the radiation reaction force with resulting orbits that were nearly circular (change in separation lower than 4%). The code was thus able to follow irrotational neutron star binaries, including radiation reaction effects, up to the merger and the formation of a differentially rotating remnant, which is stable against immediate gravitational collapse for reasonably stiff equations of state. All the results agreed pretty well with previous relativistic calculations.

6.3.2 Black-hole-neutron-star binaries

A similar combination of numerical techniques has been used by Faber et al. [74] to compute the dynamic evolution of merging black-hole-neutron-star binaries. In addition to the conformally-flat approximation and similar to Taniguchi et al. [209], Faber et al. [74] considered only the case of an extremely large mass ratio between the black hole and the neutron star, thus holding the black hole position fixed and restricting the spectral computational grid to the neighborhood of the neutron star. The metric describing the space surrounding the black hole was thus, supposed to keep the form of a Schwarzschild black hole in isotropic coordinates. The neutron star was restricted to low compactness (only a few percent) in order to have systems that disrupt well outside the last stable orbit. The system was considered to be in corotation and, just as for neutron star binaries, the gravitational radiation reaction was added by hand. As stated above, the numerical methods used SPH discretization to treat dynamic evolution of matter, and the spectral library Lorene [99] to solve the Einstein field Poisson-like equations in the conformally-flat approximation. But here, the spectral domains associated with the neutron star did not extend to radial infinity (no compactified domain) and approximate boundary conditions were imposed, using a multipole expansion of the fields. The main reason being that the black hole central singularity could not be well described on the neutron star grid.

Faber et al. [74] have studied the evolution of neutron-star-black-hole binaries with different polytropic indices for the neutron star matter equation of state, the initial data being obtained as solutions of the conformal thin-sandwich decomposition of Einstein’s equations. They found that, at least for some systems, the mass transfer from the neutron star to the black hole plays an important role in the dynamics of the system. For most of these systems, the onset of tidal disruption occurred outside the last stable orbit, contrary to what had been previously proposed in analytical models. Moreover, they have not found any evidence for significant shocks within the body of the neutron star. This star possibly expanded during the mass loss, eventually losing mass outward and inward provided that it was not too far within the last stable orbit. Although the major part of released matter remained bound to the black hole, a significant fraction could be ejected with sufficient velocity to become unbound from the binary system.

6.3.3 Black hole binaries

Encouraging results concerning black-hole-binary simulations with spectral methods have been first obtained by Scheel et al. [188]. They have used two coordinate frames to describe the motion of black holes in the spectral grid. Indeed, when using excision techniques (punctures are not regular enough to be well represented by spectral methods), excision boundaries are fixed on the numerical grid. This can cause severe problems when, due to the movement of the black hole, the excision surface becomes timelike and the whole evolution problem becomes ill-posed in the absence of boundary conditions. One solution seems to be the use of comoving coordinates, but the authors report that the GH formulation they use appear to be unstable with this setting. They, therefore, consider a first system of inertial coordinates (with respect to spatial infinity) to define the tensor components in the triad associated with these coordinates, and a second system of comoving (in some sense) coordinates. In the case of their black-hole-binary tests [188], they define the comoving coordinates dynamically, with a feedback control system that adjusts the moving coordinate frame to control the location of each apparent horizon center.

The spectral code uses 44 domains of different types (spherical and cylindrical shells, rectangular blocks) to describe the binary system. Most of the numerical strategy to integrate Einstein’s equations is taken from the tests on the GH formulation of Lindblom et al. [137] and has already been detailed in Section 6.2.1. The important technical ingredient detailed by Scheel et al. [188] is the particular filtering of tensor fields in terms of spherical harmonics. The dual-coordinate-frame representation can mix the tensor’s spherical harmonic components. So, in their filtering of the highest-order tensor spherical-harmonic coefficients, Scheel et al. [188] had to take into account this mixing by transforming spatial tensors into a rotating-frame tensor spherical-harmonic basis before filtering and then transforming back to an inertial frame basis. This method allowed them to evolve black-hole-binary spacetimes for more than four orbits, until t ≳ 600 M_ADM.

However, a central problem has been the capability of the code to follow the merger phase, and even though the code was able to compute the inspiral quite accurately, it used to fail just before the black holes merged. The problem was that, when the black holes came close to each other, their horizons became extremely distorted and strong gradients would develop in the dynamic fields. This has been explained as a gauge effect, coming from the incapacity of the gauge condition to react and change the geometry when the two black holes begin to interact strongly, and can be seen as a coordinate singularity developing close to the merger. Nevertheless, a cure has been found, as explained in Scheel et al. [185]. The original gauge is kept until some given time and then smoothly changed to a new one, based on the gauge treatment by Pretorius [176, 175] (for the lapse): the gauge source function is evolved through a damped, driven wave equation, which drives the lapse toward unity and the shift vector toward zero near the horizons. Thus, the horizons expand in coordinate space and the dynamic fields are smoothed out near the horizons, preventing gauge singularities from developing. With this transition of the gauge condition, the evolution of the black holes can be tracked until the formation of a common horizon encompassing both black holes. Then, the evolution of this single-distorted dynamic black hole is achieved by first interpolating all variables onto a new computational domain containing only one excised region, then by choosing a new comoving coordinate system, and finally by again modifying the gauge condition to drive the shift vector to a time-independent state.

These new gauge conditions have allowed Scheel et al. [185] to follow the inspiral during 16 orbits, and the merger and ring-down phase of an equal-mass nonspinning black-hole-binary system. They were able to compute the mass and the spin of the final black hole with very high accuracy (10⁻⁵ and 10⁻⁴ relative accuracy for the mass and spin, respectively), and to extract the physical waveform accurately to 0.01 radians in phase. This is the first spectral numerical simulation of the full evolution of a black-hole-binary system.

7 Conclusions

We would like to conclude our overview of spectral methods in numerical relativity by pointing out a few items that we feel are particularly interesting.

7.1 Strengths and weaknesses

The main advantage of spectral methods, especially with respect to finite difference ones, is the very rapid convergence of the numerical approximation to the real function. This implies that very high accuracy can usually be reached with only a moderate number of points. This obviously makes the codes both faster and less demanding on memory. Various examples of convergence can be found in Section 2. However, this rapid convergence is only achieved for ${{\mathcal C}^\infty}$ functions. Indeed, when the functions are less continuous, spurious oscillations appear and the convergence only follows a power law. In the case of discontinuous functions, this is known as the Gibbs phenomenon (see the extreme case of Figure 11). Gibbs-like phenomena are very likely to prevent codes from converging or to make time evolutions unstable. So spectral methods must rely heavily on the domain decomposition of space and the domains must be chosen so that the various discontinuities lie at the boundaries. Because of this, spectral methods are usually more difficult to implement than standard finite differences (see, for instance, the intricate mappings of [7]). The situation is even more complicated when the surfaces of discontinuities are not known in advance or have complicated shapes.

Spectral methods are also very efficient at dealing with problems that are related to coordinate singularities. Indeed, if the basis functions fulfill the regularity requirements, then all the functions will automatically satisfy them. In particular, it makes the use of spherical coordinates much easier than with other methods, as explained in Section 3.2.

Another nice feature is the fact that a function can be represented either by its coefficients or its values at the collocation points. Depending on the operation one has to perform, it is easier to work with the one representation or the other. When working in the coefficient space, one takes full advantage of the nonlocality of the spectral representation. A lot of operations that would be difficult otherwise can then be easily performed, like computing the ratio of two quantities vanishing at the same point (see, for instance, [81]).

7.2 Combination with other methods Spectral methods have also demonstrated that they can be a valuable tool when combined with other methods. For instance, when shocks are present, spectral methods alone have trouble dealing with discontinuities at the shock interface. However, this can be efficiently dealt with using Godunov methods. Such a combination has already been successfully applied to the simulation of the oscillations of compact stars in [71] and of core collapse [164].

Spectral methods have also been used in conjunction with a description of the fluid based on SPH (smoothed particle hydrodynamics) in the case of neutron star binaries [75] and for the merger of a neutron star with a black hole [74]. In both cases, the fluid is described by an ensemble of particles to which forces are applied. Such technique can account for complicated fluid configurations, like the spiral arms that are formed during the merger. Such arms would be tricky to follow by means of spectral methods alone. On the other hand, the equations describing gravity are nicely solved by spectral solvers.

7.3 Future developments

Finally, we would like to point out a few directions could lead to interesting results. Of course, we are not aware of what the other groups have planned for the future.

Appropriate choice of coordinates is evidently important. However, for binary systems, rather few results have been obtained using the natural choice of bispherical coordinates. So far, variations of such coordinates have only been used by Ansorg and collaborators and only in the context of initial data [8, 6, 7]. We believe that applying these coordinates, or similar coordinates, to evolutionary codes could lead to interesting results, in terms of both speed and accuracy.

The application of spectral methods to theories more complicated than general relativity is also imaginable. One of the possible fields of application is the study of branes, where there is an additional dimension to spacetime. The fact that spectral methods are accurate with relatively few degrees of freedom makes them a good candidate for simulating systems with extra dimensions. The addition of gauge fields is also something that could be studied with spectral methods, to investigate the possibility of “hairy” black holes, for instance. Of course, these are just a few ideas of what the future applications of spectral methods to the field of relativity might be. —