Abstract
I review the development of numerical evolution codes for general relativity based upon the characteristic initial value problem. Progress is traced from the early stage of 1D feasibility studies to 2D axisymmetric codes that accurately simulate the oscillations and gravitational collapse of relativistic stars and to current 3D codes that provide pieces of a binary black hole spacetime. Cauchy codes have now been successful at simulating all aspects of the binary black hole problem inside an artificially constructed outer boundary. A prime application of characteristic evolution is to eliminate the role of this artificial outer boundary via Cauchy-characteristic matching, by which the radiated waveform can be computed at null infinity. Progress in this direction is discussed.
Similar content being viewed by others
1 Introduction
It is my pleasure to review progress in numerical relativity based upon characteristic evolution. In the spirit of Living Reviews in Relativity, I invite my colleagues to continue to send me contributions and comments at winicour@pitt.edu.
We are now in an era in which Einstein’s equations can effectively be considered solved at the local level. Several groups, as reported here and in other Living Reviews in Relativity, have developed 3D codes which are stable and accurate in some sufficiently local setting. Since my last review, the pioneering works [195] (based upon a harmonic formulation) and [66, 19] (based upon BSSN formulations [218, 32]) have initiated dramatic progress in the ability of Cauchy codes to simulate the inspiral and merger of binary black holes, the premier problem in classical relativity. These codes evolve the spacetime inside an artificially constructed outer boundary. Global solutions of binary black holes are another matter. In particular, none of the existing codes are capable of computing the waveform of the gravitational radiation emanating from a binary inspiral with only the error introduced by the numerical approximation. The best that these Cauchy codes by themselves can provide is an extraction of the waveform based upon the analytical approximation that the outer boundary is at infinity. Just as several coordinate patches are necessary to describe a spacetime with nontrivial topology, the most effective attack on the binary black hole waveform might involve a global solution patched together from pieces of spacetime handled by a combination of different codes and techniques.
Most of the effort in numerical relativity has centered about the Cauchy {3 + 1} formalism [253], with the gravitational radiation extracted by perturbative methods based upon introducing an artificial Schwarzschild background in the exterior region [1, 4, 2, 3, 208, 204, 177]. These wave extraction methods have not been thoroughly tested in a nonlinear 3D setting. A different approach which is specifically tailored to study radiation is based upon the characteristic initial value problem. In the 1960s, Bondi [53, 54] and Penrose [187] pioneered the use of null hypersurfaces to describe gravitational waves. Their new approach has flourished in general relativity. It led to the first unambiguous description of gravitational radiation in a fully nonlinear context. By formulating asymptotic flatness in terms of characteristic hypersurfaces extending to infinity, they were able to reconstruct, in a nonlinear geometric setting, the basic properties of gravitational waves which had been developed in linearized theory on a Minkowski background. The major new nonlinear features were the Bondi mass and news function, and the mass loss formula relating them. The Bondi news function is an invariantly defined complex radiation amplitude N = N⊕+ iN⊗, whose real and imaginary parts correspond to the time derivatives ∂th⊕ and ∂th⊗ of the “plus” and “cross” polarization modes of the strain h incident on a gravitational wave antenna. The corresponding waveforms are important both for the design of detection templates for a binary black hole inspiral and merger and for the determination of the resulting recoil velocity.
The recent success of Cauchy evolutions in simulating binary black holes emphasizes the need of applying these global techniques to accurate waveform extraction. This has stimulated several attempts to increase the accuracy of characteristic evolution. The successful Cauchy simulation of binary black holes has been based upon adaptive mesh techniques and upon fourth order finite difference approximations. The initial characteristic codes were developed with unigrid second order accuracy. One of the prime factors affecting the accuracy of any characteristic code is the introduction of a smooth coordinate system covering the sphere, which labels the null directions on the outgoing light cones. This is also an underlying problem in meteorology and oceanography. In a pioneering paper on large-scale numerical weather prediction, Phillips [189] put forward a list of desirable features for a mapping of the sphere to be useful for global forecasting. The first requirement was the freedom from singularities. This led to two distinct choices which had been developed earlier in purely geometrical studies: stereographic coordinates (two coordinate patches) and cubed-sphere coordinates (six patches). Both coordinate systems have been rediscovered in the context of numerical relativity (see Section 4.1). The cubed-sphere method has stimulated two new attempts at improved codes for characteristic evolution (see Section 4.2.3).
Another issue affecting code accuracy is the choice between a second vs first differential order reduction of the evolution system. Historically, the predominant importance of computational fluid dynamics has favored first order systems, in particular the reduction to symmetric hyperbolic form. However, in acoustics and elasticity theory, where the natural treatment is in terms of second order wave equations, an effective argument for the second order form has been made [159]. In general relativity, the question of whether first or second order formulations are more natural depends on how Einstein’s equations are reduced to a hyperbolic system by some choice of coordinates and variables. The second order form is more natural in the harmonic formulation, where the Einstein equations reduce to quasilinear wave equations. The first order form is more natural in the Friedrich-Nagy formulation, which includes the Weyl tensor among the evolution variables, and was used in the first demonstration of a well-posed initial-boundary value problem for Einstein’s equations. Recent investigations of first order formulations of the characteristic initial value problem are discussed in Section 4.2.2.
The major drawback of a stand-alone characteristic approach arises from the formation of caustics in the light rays generating the null hypersurfaces. In the most ambitious scheme proposed at the theoretical level such caustics would be treated “head-on” as part of the evolution problem [233]. This is a profoundly attractive idea. Only a few structural stable caustics can arise in numerical evolution, and their geometrical properties are well enough understood to model their singular behavior numerically [99], although a computational implementation has not yet been attempted.
In the typical setting for the characteristic initial value problem, the domain of dependence of a single smooth null hypersurface is empty. In order to obtain a nontrivial evolution problem, the null hypersurface must either be completed to a caustic-crossover region where it pinches off, or an additional inner boundary must be introduced. So far, the only caustics that have been successfully evolved numerically in general relativity are pure point caustics (the complete null cone problem). When spherical symmetry is not present, the stability conditions near the vertex of a light cone place a strong restriction on the allowed time step [124]. Nevertheless, point caustics in general relativity have been successfully handled for axisymmetric vacuum spacetimes [120]. Progress toward extending these results to realistic astrophysical sources has been made in two Ph.D. theses based upon characteristic evolution codes. Florian Siebel’s thesis work [219], at the Technische Universität München, integrated an axisymmetric characteristic gravitational-hydro code with a high resolution shock capturing code for the relativistic hydrodynamics. This coupled general relativistic code has been thoroughly tested and has yielded state-of-the-art results for the gravitational waves produced by the oscillation and collapse of a relativistic star (see Sections 7.1 and 7.2). Nevertheless, computational demands to extend these results to 3D evolution would be prohibitive using current generation supercomputers, due to the small timestep required at the vertex of the null cone (see Section 3.3). This is unfortunate because, away from the caustics, characteristic evolution offers myriad computational and geometrical advantages. Vacuum simulations of black hole spacetimes, where the inner boundary can be taken to be the white hole horizon, offer a scenario where both the timestep and caustic problems can be avoided and three-dimensional simulations are practical. In Yosef Zlochower’s thesis work [255], at the University of Pittsburgh, the gravitational waves generated from the post-merger phase of a binary black black hole were computed using a fully nonlinear three-dimensional characteristic code [256] (see Section 4.5). He showed how the characteristic code could be employed to investigate the nonlinear mode coupling in the response of a black hole to the infall of gravitational waves.
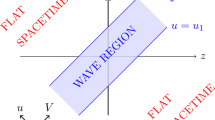
At least in the near future, fully three-dimensional computational applications of characteristic evolution are likely to be restricted to some mixed form, in which data is prescribed on a non-singular but incomplete initial null hypersurface N and on a second inner boundary B, which together with the initial null hypersurface determine a nontrivial domain of dependence. The hypersurface B may be either (i) null, (ii) timelike or (iii) spacelike, as schematically depicted in Figure 1. The first two possibilities give rise to (i) the double null problem and (ii) the nullcone-worldtube problem. Possibility (iii) has more than one interpretation. It may be regarded as a Cauchy initial-boundary value problem where the outer boundary is null. An alternative interpretation is the Cauchy-characteristic matching (CCM) problem, in which the Cauchy and characteristic evolutions are matched transparently across a worldtube W, as indicated in Figure 1.
In CCM, it is possible to choose the matching interface between the Cauchy and characteristic regions to be a null hypersurface, but it is more practical to match across a timelike worldtube. CCM combines the advantages of characteristic evolution in treating the outer radiation zone in spherical coordinates which are naturally adapted to the topology of the worldtube with the advantages of Cauchy evolution in treating the inner region in Cartesian coordinates, where spherical coordinates would break down.
In this review, we trace the development of characteristic algorithms from model 1D problems to a 2D axisymmetric code which computes the gravitational radiation from the oscillation and gravitational collapse of a relativistic star and to a 3D code designed to calculate the waveform emitted in the merger to ringdown phase of a binary black hole. And we trace the development of CCM from early feasibility studies to successful implementation in the linear regime and through current attempts to treat the binary black hole problem.
A major achievement has been the successful application of CCM to the linearized matching problem between a 3D characteristic code and a 3D Cauchy code based upon harmonic coordinates [236] (see Section 5.8). Here the linearized Cauchy code satisfies a well-posed initial-boundary value problem, which seems to be a critical missing ingredient in previous attempts at CCM in general relativity. Recently a well-posed initial-boundary value problem has been established for fully nonlinear harmonic evolution [162] (see Section 5.3), which should facilitate the extension of CCM to the nonlinear case.
In previous reviews, I tried to include material on the treatment of boundaries in the computational mathematics and fluid dynamics literature because of its relevance to the CCM problem. The fertile growth of this subject warrants a separate Living Review in Relativity on boundary conditions, which is presently under consideration. In anticipation of this, I will not attempt to keep this subject up to date except for material of direct relevance to CCM. See [213] for an independent review of boundary conditions that have been used in numerical relativity.
The problem of computing the evolution of a neutron star, in close orbit about a black hole is of clear importance to the new gravitational wave detectors. The interaction with the black hole could be strong enough to produce a drastic change in the emitted waves, say by tidally disrupting the star, so that a perturbative calculation would be inadequate. The understanding of such nonlinear phenomena requires well behaved numerical simulations of hydrodynamic systems satisfying Einstein’s equations. Several numerical relativity codes for treating the problem of a neutron star near a black hole have been developed, as described in the Living Review in Relativity on “Numerical Hydrodynamics in General Relativity” by Font [91]. Although most of these efforts concentrate on Cauchy evolution, the characteristic approach has shown remarkable robustness in dealing with a single black hole or relativistic star. In this vein, state-of-the-art axisymmetric studies of the oscillation and gravitational collapse of relativistic stars have been achieved (see Section 7.2) and progress has been made in the 3D simulation of a body in close orbit about a Schwarzschild black hole (see Sections 4.6 and 7.3).
2 The Characteristic Initial Value Problem
Characteristics have traditionally played an important role in the analysis of hyperbolic partial differential equations. However, the use of characteristic hypersurfaces to supply the foliation underlying an evolution scheme has been mainly restricted to relativity. This is perhaps natural because in curved spacetime there is no longer a preferred Cauchy foliation provided by the Euclidean 3-spaces allowed in Galilean or special relativity. The method of shooting along characteristics is a standard technique in many areas of computational physics, but evolution based upon characteristic hypersurfaces is quite uniquely limited to relativity.
Bondi’s initial use of null coordinates to describe radiation fields [53] was followed by a rapid development of other null formalisms. These were distinguished either as metric based approaches, as developed for axisymmetry by Bondi, Metzner and van der Burg [54] and generalized to 3 dimensions by Sachs [211], or as null tetrad approaches in which the Bianchi identities appear as part of the system of equations, as developed by Newman and Penrose [179].
At the outset, null formalisms were applied to construct asymptotic solutions at null infinity by means of 1/r expansions. Soon afterward, Penrose [187] devised the conformal compactification of null infinity \({\mathcal I}\) (“scri”), thereby reducing to geometry the asymptotic quantities describing the physical properties of the radiation zone, most notably the Bondi mass and news function. The characteristic initial value problem rapidly became an important tool for the clarification of fundamental conceptual issues regarding gravitational radiation and its energy content. It laid bare and geometrised the gravitational far field.
The initial focus on asymptotic solutions clarified the kinematic properties of radiation fields but could not supply the dynamical properties relating the waveform to a specific source. It was soon realized that instead of carrying out a 1/r expansion, one could reformulate the approach in terms of the integration of ordinary differential equations along the characteristics (null rays) [237]. The integration constants supplied on some inner boundary then played the role of sources in determining the specific waveforms obtained at infinity. In the double-null initial value problem of Sachs [212], the integration constants are supplied at the intersection of outgoing and ingoing null hypersurfaces. In the worldtube-nullcone formalism, the sources were represented by integration constants on a timelike worldtube [237]. These early formalisms have gone through much subsequent revamping. Some have been reformulated to fit the changing styles of modern differential geometry. Some have been reformulated in preparation for implementation as computational algorithms. The articles in [83] give a representative sample of formalisms. Rather than including a review of the extensive literature on characteristic formalisms in general relativity, I concentrate here on those approaches which have been implemented as computational evolution schemes. The well-posedness of the associated initial-boundary value problems, which is essential for the success of numerical simulations, is treated in a separate Living Review in Relativity on “Theorems on Existence and Global Dynamics for the Einstein Equations” by Rendall [203].
All characteristic evolution schemes share the same skeletal form. The fundamental ingredient is a foliation by null hypersurfaces u = const. which are generated by a two-dimensional set of null rays, labeled by coordinates xA, with a coordinate λ varying along the rays. In (u, λ, xA) null coordinates, the main set of Einstein equations take the schematic form
and
Here F represents a set of hypersurface variables, G a set of evolution variables, and HF and HG are nonlinear hypersurface operators, i.e. they operate locally on the values of F, G and G,u intrinsic to a single null hypersurface. In the Bondi formalism, these hypersurface equations have a hierarchical structure in which the members of the set F can be integrated in turn in terms of the characteristic data for the evolution variables and the computed values of prior members of the hierarchy. In addition to these main Einstein equations, there is a subset of four subsidiary Einstein equations which are satisfied by virtue of the Bianchi identities, provided that they are satisfied on a hypersurface transverse to the characteristics. These equations have the physical interpretation as conservation laws. Mathematically they are analogous to the constraint equations of the canonical formalism. But they are not elliptic since they may be intrinsic to null or timelike hypersurfaces, rather than spacelike Cauchy hypersurfaces.
Computational implementation of characteristic evolution may be based upon different versions of the formalism (i.e. metric or tetrad) and different versions of the initial value problem (i.e. double null or worldtube-nullcone). The performance and computational requirements of the resulting evolution codes can vary drastically. However, most characteristic evolution codes share certain common advantages:
-
The characteristic initial data is free, i.e. there are no elliptic constraints on the data. This eliminates the need for time consuming iterative constraint solvers with their accompanying artificial boundary conditions. This flexibility and control in prescribing initial data has the trade-off of limited experience with prescribing physically realistic characteristic initial data.
-
The coordinates are very “rigid”, i.e. there is very little remaining gauge freedom.
-
The constraints satisfy ordinary differential equations along the characteristics which force any constraint violation to fall off asymptotically as 1/r2.
-
No second time derivatives appear so that the number of basic variables is at most half the number for the corresponding version of the Cauchy problem.
-
The main Einstein equations form a system of coupled ordinary differential equations with respect to the parameter λ varying along the characteristics. This allows construction of an evolution algorithm in terms of a simple march along the characteristics.
-
In problems with isolated sources, the radiation zone can be compactified into a finite grid boundary with the metric rescaled by 1/r2 as an implementation of Penrose’s conformal boundary at future null infinity \({{\mathcal I}^ +}\). Because \({{\mathcal I}^ +}\) is a null hypersurface, no extraneous outgoing radiation condition or other artificial boundary condition is required. The analogous treatment in the Cauchy problem requires the use of hyperboloidal spacelike hypersurfaces asymptoting to null infinity [96]. For reviews of the hyperboloidal approach and its status in treating the associated three-dimensional computational problem, see [148, 92].
-
The grid domain is exactly the region in which waves propagate, which is ideally efficient for radiation studies. Since each null hypersurface of the foliation extends to infinity, the radiation is calculated immediately (in retarded time).
-
In black hole spacetimes, a large redshift at null infinity relative to internal sources is an indication of the formation of an event horizon and can be used to limit the evolution to the exterior region of spacetime. While this can be disadvantageous for late time accuracy, it allows the possibility of identifying the event horizon “on the fly”, as opposed to Cauchy evolution where the event horizon can only be located after the evolution has been completed.
Perhaps most important from a practical view, characteristic evolution codes have shown remarkably robust stability and were the first to carry out long term evolutions of moving black holes [116].
Characteristic schemes also share as a common disadvantage the necessity either to deal with caustics or to avoid them altogether. The scheme to tackle the caustics head on by including their development and structure as part of the evolution is perhaps a great idea still ahead of its time but one that should not be forgotten. There are only a handful of structurally stable caustics, and they have well known algebraic properties. This makes it possible to model their singular structure in terms of Padé approximants. The structural stability of the singularities should in principle make this possible, and algorithms to evolve the elementary caustics have been proposed [79, 230]. In the axisymmetric case, cusps and folds are the only structurally stable caustics, and they have already been identified in the horizon formation occurring in simulations of head-on collisions of black holes and in the temporarily toroidal horizons occurring in collapse of rotating matter [172, 217]. In a generic binary black hole horizon, where axisymmetry is broken, there is a closed curve of cusps which bounds the two-dimensional region on the event horizon where the black holes initially form and merge [165, 150].
3 Prototype Characteristic Evolution Codes
Limited computer power, as well as the instabilities arising from non-hyperbolic formulations of Einstein’s equations, necessitated that the early code development in general relativity be restricted to spacetimes with symmetry. Characteristic codes were first developed for spacetimes with spherical symmetry. The techniques for other special relativistic fields which propagate on null characteristics are similar to the gravitational case. Such fields are included in this section. We postpone treatment of relativistic fluids, whose characteristics are timelike, until Section 7.
3.1 {1 + 1}-dimensional codes
It is often said that the solution of the general ordinary differential equation is essentially known, in light of the success of computational algorithms and present day computing power. Perhaps this is an overstatement because investigating singular behavior is still an art. But, in this spirit, it is fair to say that the general system of hyperbolic partial differential equations in one spatial dimension seems to be a solved problem in general relativity. Codes have been successful in revealing important new phenomena underlying singularity formation in cosmology [36] and in dealing with unstable spacetimes to discover critical phenomena [127]. As described below, characteristic evolution has contributed to a rich variety of such results.
One of the earliest characteristic evolution codes, constructed by Corkill and Stewart [79, 229], treated spacetimes with two Killing vectors using a grid based upon double null coordinates, with the null hypersurfaces intersecting in the surfaces spanned by the Killing vectors. They simulated colliding plane waves and evolved the Khan-Penrose [157] collision of impulsive (δ-function curvature) plane waves to within a few numerical zones from the final singularity, with extremely close agreement with the analytic results. Their simulations of collisions with more general waveforms, for which exact solutions are not known, provided input to the understanding of singularity formation which was unforeseen in the analytic treatments of this problem.
Many {1 + 1}-dimensional characteristic codes have been developed for spherically symmetric systems. Here matter must be included in order to make the system non-Schwarzschild. Initially the characteristic evolution of matter was restricted to simple cases, such as massless Klein-Gordon fields, which allowed simulation of gravitational collapse and radiation effects in the simple context of spherical symmetry. Now, characteristic evolution of matter is progressing to more complicated systems. Its application to hydrodynamics has made significant contributions to general relativistic astrophysics, as reviewed in Section 7.
The synergy between analytic and computational approaches has led to dramatic results in the massless Klein-Gordon case. On the analytic side, working in a characteristic initial value formulation based upon outgoing null cones, Christodoulou made a penetrating study of the spherically symmetric problem [69, 70, 71, 72, 73, 74]. In a suitable function space, he showed the existence of an open ball about Minkowski space data whose evolution is a complete regular spacetime; he showed that an evolution with a nonzero final Bondi mass forms a black hole; he proved a version of cosmic censorship for generic data; and he established the existence of naked singularities for non-generic data. What this analytic tour-de-force did not reveal was the remarkable critical behavior in the transition to the black hole regime, which was discovered by Choptuik [67, 68] in simulations using Cauchy evolution. This phenomenon has now been understood in terms of the methods of renormalization group theory and intermediate asymptotics, and has spawned a new subfield in general relativity, which is covered in the Living Review in Relativity on “Critical Phenomena in Gravitational Collapse” by Gundlach [127].
The characteristic evolution algorithm for the spherically symmetric Einstein-Klein-Gordon problem provides a simple illustration of the techniques used in the general case. It centers about the evolution scheme for the scalar field, which constitutes the only dynamical field. Given the scalar field, all gravitational quantities can be determined by integration along the characteristics of the null foliation. This is a coupled problem, since the scalar wave equation involves the curved space metric. It illustrates how null algorithms lead to a hierarchy of equations which can be integrated along the characteristics to effectively decouple the hypersurface and dynamical variables.
In a Bondi coordinate system based upon outgoing null hypersurfaces u = const. and a surface area coordinate r, the metric is
Smoothness at r = 0 allows imposition of the coordinate conditions
The field equations consist of the curved space wave equation □Φ = 0 for the scalar field and two hypersurface equations for the metric functions:
The wave equation can be expressed in the form
where g = rΦ and □(2) is the D’Alembertian associated with the two-dimensional submanifold spanned by the ingoing and outgoing null geodesics. Initial null data for evolution consists of Φ(u0, r) at the initial retarded time u0.
Because any two-dimensional geometry is conformally flat, the surface integral of □(2)g over a null parallelogram Σ gives exactly the same result as in a flat 2-space, and leads to an integral identity upon which a simple evolution algorithm can be based [122]. Let the vertices of the null parallelogram be labeled by N, E, S, and W corresponding, respectively, to their relative locations (North, East, South, and West) in the 2-space, as shown in Figure 2. Upon integration of Equation (7), curvature introduces an integral correction to the flat space null parallelogram relation between the values of g at the vertices:
This identity, in one form or another, lies behind all of the null evolution algorithms that have been applied to this system. The prime distinction between the different algorithms is whether they are based upon double null coordinates, or upon Bondi coordinates as in Equation (3). When a double null coordinate system is adopted, the points N, E, S, and W can be located in each computational cell at grid points, so that evaluation of the left hand side of Equation (8) requires no interpolation. As a result, in flat space, where the right hand side of Equation (8) vanishes, it is possible to formulate an exact evolution algorithm. In curved space, of course, there is a truncation error arising from the approximation of the integral, e.g., by evaluating the integrand at the center of Σ.
The identity (8) gives rise to the following explicit marching algorithm, indicated in Figure 2. Let the null parallelogram lie at some fixed θ and ϕ and span adjacent retarded time levels u0 and u0 + Δu. Imagine for now that the points N, E, S, and W lie on the spatial grid, with rN − rW = rE − rS = Δr. If g has been determined on the entire initial cone u0, which contains the points E and S, and g has been determined radially outward from the origin to the point W on the next cone u0 +Δu, then Equation (8) determines g at the next radial grid point N in terms of an integral over Σ. The integrand can be approximated to second order, i.e. to \({\mathcal O}(\Delta r\Delta u)\), by evaluating it at the center of Σ. To this same accuracy, the value of g at the center equals its average between the points E and W, at which g has already been determined. Similarly, the value of (V/r),r at the center of Σ can be approximated to second order in terms of values of V at points where it can be determined by integrating the hypersurface equations (5, 6) radially outward from r = 0.
After carrying out this procedure to evaluate g at the point N, the procedure can then be iterated to determine g at the next radially outward grid point on the u0 +Δu level, i.e. point n in Figure 2. Upon completing this radial march to null infinity, in terms of a compactified radial coordinate such as x = r/(1 + r), the field g is then evaluated on the next null cone at u0+ 2Δu, beginning at the vertex where smoothness gives the startup condition that g(u, 0) = 0.
In the compactified Bondi formalism, the vertices N, E, S, and W of the null parallelogram Σ cannot be chosen to lie exactly on the grid because, even in Minkowski space, the velocity of light in terms of a compactified radial coordinate x is not constant. As a consequence, the fields g, β, and V at the vertices of Σ are approximated to second order accuracy by interpolating between grid points. However, cancellations arise between these four interpolations so that Equation (8) is satisfied to fourth order accuracy. The net result is that the finite difference version of Equation (8) steps g radially outward one zone with an error of fourth order in grid size, \({\mathcal O}({({\Delta _u})^2}{(\Delta x)^2})\). In addition, the smoothness conditions (4) can be incorporated into the startup for the numerical integrations for V and β to insure no loss of accuracy in starting up the march at r = 0. The resulting global error in g, after evolving a finite retarded time, is then \({\mathcal O}(\Delta u\Delta x)\), after compounding errors from 1/(ΔuΔx) number of zones.
When implemented on a grid based upon the (u, r) coordinates, the stability of this algorithm is subject to a Courant-Friedrichs-Lewy (CFL) condition requiring that the physical domain of dependence be contained in the numerical domain of dependence. In the spherically symmetric case, this condition requires that the ratio of the time step to radial step be limited by (V/r) Δu ≤ 2Δr, where Δr = Δ[x/(1−x)]. This condition can be built into the code using the value V/r = e2H, corresponding to the maximum of V/r at \({{\mathcal I}^ +}\). The strongest restriction on the time step then arises just before the formation of a horizon, where V/r → ∞ at \({{\mathcal I}^ +}\). This infinite redshift provides a mechanism for locating the true event horizon “on the fly” and restricting the evolution to the exterior spacetime. Points near \({{\mathcal I}^ +}\) must be dropped in order to evolve across the horizon due to the lack of a nonsingular compactified version of future time infinity I+.
The situation is quite different in a double null coordinate system, in which the vertices of the null parallelogram can be placed exactly on grid points so that the CFL condition is automatically satisfied. A characteristic code based upon double null coordinates was developed by Goldwirth and Piran in a study of cosmic censorship [109] based upon the spherically symmetric gravitational collapse of a massless scalar field. Their early study lacked the sensitivity of adaptive mesh refinement (AMR) which later enabled Choptuik to discover the critical phenomena appearing in this problem. Subsequent work by Marsa and Choptuik [171] combined the use of the null related ingoing Eddington-Finklestein coordinates with Unruh’s strategy of singularity excision to construct a 1D code that “runs forever”. Later, Garfinkle [104] constructed an improved version of the Goldwirth-Piran double null code which was able to simulate critical phenomena without using adaptive mesh refinement. In this treatment, as the evolution proceeds on one outgoing null cone to the next, the grid points follow the ingoing null cones and must be dropped as they cross the origin at r = 0. However, after half the grid points are lost they are then “recycled” at new positions midway between the remaining grid points. This technique is crucial for resolving the critical phenomena associated with an r → 0 size horizon. An extension of the code [105] was later used to verify that scalar field collapse in six dimensions continues to display critical phenomena.
Hamadé and Stewart [135] also applied a double null code to study critical phenomena. In order to obtain the accuracy necessary to confirm Choptuik’s results they developed the first example of a characteristic grid with AMR. They did this with both the standard Berger and Oliger algorithm and their own simplified version, with both versions giving indistinguishable results. Their simulations of critical collapse of a massless scalar field agreed with Choptuik’s values for the universal parameters governing mass scaling and displayed the echoing associated with discrete self-similarity. Hamadé, Horne, and Stewart [134] extended this study to the spherical collapse of an axion/dilaton system and found in this case that self-similarity was a continuous symmetry of the critical solution.
Brady, Chambers, and Gonçalves [55] used Garfinkle’s [104] double null algorithm to investigate the effect of a massive scalar field on critical phenomena. The introduction of a mass term in the scalar wave equation introduces a scale to the problem, which suggests that the critical point behavior might differ from the massless case. They found that there are two different regimes depending on the ratio of the Compton wavelength 1/m of the scalar mass to the radial size λ of the scalar pulse used to induce collapse. When λm ≪ 1, the critical solution is the one found by Choptuik in the m = 0 case, corresponding to a type II phase transition. However, when λm ≫ 1, the critical solution is an unstable soliton star (see [216]), corresponding to a type I phase transition where black hole formation turns on at a finite mass.
A code based upon Bondi coordinates, developed by Husa and his collaborators [149], has been successfully applied to spherically symmetric critical collapse of a nonlinear σ-model coupled to gravity. Critical phenomena cannot be resolved on a static grid based upon the Bondi r-coordinate. Instead, the numerical techniques of Garfinkle were adopted by using a dynamic grid following the ingoing null rays and by recycling radial grid points. They studied how coupling to gravity affects the critical behavior previously observed by Bizoń [51] and others in the Minkowski space version of the model. For a wide range of the coupling constant, they observe discrete self-similarity and typical mass scaling near the critical solution. The code is shown to be second order accurate and to give second order convergence for the value of the critical parameter.
The first characteristic code in Bondi coordinates for the self-gravitating scalar wave problem was constructed by Gómez and Winicour [122]. They introduced a numerical compactification of \({{\mathcal I}^ +}\) for the purpose of studying effects of self-gravity on the scalar radiation, particularly in the high amplitude limit of the rescaling Φ → aΦ. As a → ∞, the red shift creates an effective boundary layer at \({{\mathcal I}^ +}\) which causes the Bondi mass MB and the scalar field monopole moment Q to be related by \({M_{\rm{B}}} \sim \pi \vert Q\vert/\sqrt 2\), rather than the quadratic relation of the weak field limit [122]. This could also be established analytically so that the high amplitude limit provided a check on the code’s ability to handle strongly nonlinear fields. In the small amplitude case, this work incorrectly reported that the radiation tails from black hole formation had an exponential decay characteristic of quasinormal modes rather than the polynomial 1/t or 1/t2 falloff expected from Price’s [198] work on perturbations of Schwarzschild black holes. In hindsight, the error here was not having confidence to run the code sufficiently long to see the proper late time behavior.
Gundlach, Price, and Pullin [129, 130] subsequently reexamined the issue of power law tails using a double null code similar to that developed by Goldwirth and Piran. Their numerical simulations verified the existence of power law tails in the full nonlinear case, thus establishing consistency with analytic perturbative theory. They also found normal mode ringing at intermediate time, which provided reassuring consistency with perturbation theory and showed that there is a region of spacetime where the results of linearized theory are remarkably reliable even though highly nonlinear behavior is taking place elsewhere. These results have led to a methodology that has application beyond the confines of spherically symmetric problems, most notably in the “close approximation” for the binary black hole problem [199]. Power law tails and quasinormal ringing have also been confirmed using Cauchy evolution [171].
The study of the radiation tail decay of a scalar field was subsequently extended by Gómez, Schmidt, and Winicour [125] using a characteristic code. They showed that the Newman-Penrose constant [181] for the scalar field determines the exponent of the power law (and not the static monopole moment as often stated). When this constant is non-zero, the tail decays as 1/t on \({{\mathcal I}^ +}\), as opposed to the 1/t2 decay for the vanishing case. (They also found t−n log t corrections, in addition to the exponentially decaying contributions of the quasinormal modes.) This code was also used to study the instability of a topological kink in the configuration of the scalar field [23]. The kink instability provides the simplest example of the turning point instability [152, 226] which underlies gravitational collapse of static equilibria.
Brady and Smith [57] have demonstrated that characteristic evolution is especially well adapted to explore properties of Cauchy horizons. They examined the stability of the Reissner-Nordström Cauchy horizon using an Einstein-Klein-Gordon code based upon advanced Bondi coordinates (υ,r) (where the hypersurfaces υ = const are ingoing null hypersurfaces). They studied the effect of a spherically symmetric scalar pulse on the spacetime structure as it propagates across the event horizon. Their numerical methods were patterned after the work of Goldwirth and Piran [109], with modifications of the radial grid structure that allow deep penetration inside the black hole. In accord with expectations from analytic studies, they found that the pulse first induces a weak null singularity on the Cauchy horizon, which then leads to a crushing spacelike singularity as r → 0. The null singularity is weak in the sense that an infalling observer experiences a finite tidal force, although the Newman-Penrose Weyl component Ψ2 diverges, a phenomenon known as mass inflation [193]. These results confirm the earlier result of Gnedin and Gnedin [108] that a central spacelike singularity would be created by the interaction of a charged black hole with a scalar field, in accord with a physical argument by Penrose [188] that a small perturbation undergoes an infinite redshift as it approaches the Cauchy horizon.
Burko [60] has confirmed and extended these results, using a code based upon double null coordinates which was developed with Ori [61] in a study of tail decay. He found that in the early stages the perturbation of the Cauchy horizon is weak and in agreement with the behavior calculated by perturbation theory.
Brady, Chambers, Krivan, and Laguna [56] have found interesting effects of a non-zero cosmological constant Λ on tail decay by using a characteristic Einstein-Klein-Gordon code to study the effect of a massless scalar pulse on Schwarzschild-de Sitter and Reissner-Nordström-de Sitter spacetimes. First, by constructing a linearized scalar evolution code, they show that scalar test fields with ℓ ≠ 0 have exponentially decaying tails, in contrast to the standard power law tails for asymptotically flat spacetimes. Rather than decaying, the monopole mode asymptotes at late time to a constant, which scales linearly with Λ, in contrast to the standard no-hair result. This unusual behavior for the ℓ = 0 case was then independently confirmed with a nonlinear spherical characteristic code.
Using a combination of numerical and analytic techniques based upon null coordinates, Hod and Piran have made an extensive series of investigations of the spherically symmetric charged Einstein-Klein-Gordon system dealing with the effect of charge on critical gravitational collapse [142] and the late time tail decay of a charged scalar field on a Reissner-Nordström black hole [143, 146, 144, 145]. These studies culminated in a full nonlinear investigation of horizon formation by the collapse of a charged massless scalar pulse [147]. They track the formation of an apparent horizon which is followed by a weakly singular Cauchy horizon which then develops a strong spacelike singularity at r = 0. This is in complete accord with prior perturbative results and nonlinear simulations involving a pre-existing black hole. Oren and Piran [182] increased the late time accuracy of this study by incorporating an adaptive grid for the retarded time coordinate u, with a refinement criterion to maintain Δr/r = const. The accuracy of this scheme is confirmed through convergence tests as well as charge and constraint conservation. They were able to observe the physical mechanism which prohibits black hole formation with charge to mass ration Q/M > 1. Electrostatic repulsion of the outer parts of the scalar pulse increases relative to the gravitational attraction and causes the outer portion of the charge to disperse to larger radii before the black hole is formed. Inside the black hole, they confirm the formation of a weakly singular Cauchy horizon which turns into a strong spacelike singularity, in accord with other studies.
Hod extended this combined numerical-analytical double null approach to investigate higher order corrections to the dominant power law tail [140], as well as corrections due to a general spherically symmetric scattering potential [139] and due to a time dependent potential [141]. He found (log t)/t modifications to the leading order tail behavior for a Schwarzschild black hole, in accord with earlier results of Gómez et al. [125]. These modifications fall off at a slow rate so that a very long numerical evolution (t ≈ 3000 M)is necessary to cleanly identify the leading order power law decay.
The foregoing numerical-analytical work based upon characteristic evolution has contributed to a very comprehensive classical treatment of spherically symmetric gravitational collapse. Sorkin and Piran [225] have investigated the question of quantum corrections due to pair creation on the gravitational collapse of a charged scalar field. For observers outside the black hole, several analytic studies have indicated that such pair-production can rapidly diminish the charge of the black hole. Sorkin and Piran apply the same double-null characteristic code used in studying the classical problem [147] to evolve across the event horizon and observe the quantum effects on the Cauchy horizon. The quantum electrodynamic effects are modeled in a rudimentary way by a nonlinear dielectric ϵ constant that limits the electric field to the critical value necessary for pair creation. The back-reaction of the pairs on the stress-energy and the electric current are ignored. They found that quantum effects leave the classical picture of the Cauchy horizon qualitatively intact but that they shorten its “lifetime” by hastening the conversion of the weak null singularity into a strong spacelike singularity.
The Southampton group has constructed a {1 + 1}-dimensional characteristic code for space-times with cylindrical symmetry [77, 87]. The original motivation was to use it as the exterior characteristic code in a test case of CCM (see Section 5.5.1 for the application to matching). Subsequently, Sperhake, Sjödin, and Vickers [223, 227] modified the code into a global characteristic version for the purpose of studying cosmic strings, represented by massive scalar and vector fields coupled to gravity. Using a Geroch decomposition [106] with respect to the translational Killing vector, they reduced the global problem to a {2 + 1}-dimensional asymptotically flat spacetime, so that \({{\mathcal I}^ +}\) could be compactified and included in the numerical grid. Rather than the explicit scheme used in CCM, the new version employs an implicit, second order in space and time, Crank-Nicholson evolution scheme. The code showed long term stability and second order convergence in vacuum tests based upon exact Weber-Wheeler waves [247] and Xanthopoulos’ rotating solution [252], and in tests of wave scattering by a string. The results show damped ringing of the string after an incoming Weber-Wheeler pulse has excited it and then scattered to \({{\mathcal I}^ +}\). The ringing frequencies are independent of the details of the pulse but are inversely proportional to the masses of the scalar and vector fields.
Frittelli and Gómez [101] have cast the spherically symmetric Einstein-Klein-Gordon problem in symmetric hyperbolic form, where in a Bondi-Sachs gauge the fundamental variables are the scalar field, lapse and shift. The Bondi-Sachs gauge conditions relate the usual ADM variables (the 3-metric and extrinsic curvature) to the lapse and shift, which obey simpler evolution equations. The resulting Cauchy problem is well-posed and the outer boundary condition is constraint preserving (although whether the resulting IBVP is well-posed is not addressed, i.e. whether the boundary condition is dissipative). A numerical evolution algorithm based upon the system produces a stable simulation of a scalar pulse Φ scattering off a black hole. The initial data for the pulse satisfies ∂tΦ = 0 so, as expected, it contains an ingoing part, which crosses the horizon, and an outgoing part, which leaves the grid at the outer boundary with a small amount of back reflection.
3.1.1 Adaptive mesh refinement
The goal of computing waveforms from relativistic binaries, such as a neutron star or stellar mass back hole spiraling into a supermassive black hole, requires more than a stable convergent code. It is a delicate task to extract a waveform in a spacetime in which there are multiple length scales: the size of the supermassive black hole, the size of the star, the wavelength of the radiation. It is commonly agreed that some form of mesh refinement is essential to attack this problem. Mesh refinement was first applied in characteristic evolution to solve specific spherically symmetric problems regarding critical phenomena and singularity structure [104, 135, 60].
Pretorius and Lehner [197] have presented a general approach for AMR to a generic characteristic code. Although the method is designed to treat 3D simulations, the implementation has so far been restricted to the Einstein-Klein-Gordon system in spherical symmetry. The 3D approach is modeled after the Berger and Oliger AMR algorithm for hyperbolic Cauchy problems, which is reformulated in terms of null coordinates. The resulting characteristic AMR algorithm can be applied to any unigrid characteristic code and is amenable to parallelization. They applied it to the problem of a spherically symmetric massive Klein-Gordon field propagating outward from a black hole. The non-zero rest mass restricts the Klein-Gordon field from propagating to infinity. Instead it diffuses into higher frequency components which Pretorius and Lehner show can be resolved using AMR but not with a comparison unigrid code.
3.2 {2 + 1}-dimensional codes
One-dimensional characteristic codes enjoy a very special simplicity due to the two preferred sets (ingoing and outgoing) of characteristic null hypersurfaces. This eliminates a source of gauge freedom that otherwise exists in either two- or three-dimensional characteristic codes. However, the manner in which the characteristics of a hyperbolic system determine domains of dependence and lead to propagation equations for shock waves is the same as in the one-dimensional case. This makes it desirable for the purpose of numerical evolution to enforce propagation along characteristics as extensively as possible. In basing a Cauchy algorithm upon shooting along characteristics, the infinity of characteristic rays (technically, bicharacteristics) at each point leads to an arbitrariness which, for a practical numerical scheme, makes it necessary either to average the propagation equations over the sphere of characteristic directions or to select out some preferred subset of propagation equations. The latter approach was successfully applied by Butler [62] to the Cauchy evolution of two-dimensional fluid flow, but there seems to have been very little follow-up along these lines. The closest resemblance is the use of Riemann solvers for high resolution shock capturing in hydrodynamic codes (see Section 7.1).
The formal ideas behind the construction of two- or three-dimensional characteristic codes are similar, although there are various technical options for treating the angular coordinates which label the null rays. Historically, most characteristic work graduated first from 1D to 2D because of the available computing power.
3.3 The Bondi problem
The first characteristic code based upon the original Bondi equations for a twist-free axisymmetric spacetime was constructed by J. Welling in his PhD thesis at Pittsburgh [153]. The spacetime was foliated by a family of null cones, complete with point vertices at which regularity conditions were imposed. The code accurately integrated the hypersurface and evolution equations out to compactified null infinity. This allowed studies of the Bondi mass and radiation flux on the initial null cone, but it could not be used as a practical evolution code because of instabilities.
These instabilities came as a rude shock and led to a retreat to the simpler problem of axisymmetric scalar waves propagating in Minkowski space, with the metric
in outgoing null cone coordinates. A null cone code for this problem was constructed using an algorithm based upon Equation (8), with the angular part of the flat space Laplacian replacing the curvature terms in the integrand on the right hand side. This simple setting allowed one source of instability to be traced to a subtle violation of the CFL condition near the vertices of the cones. In terms of the grid spacing Δxα, the CFL condition in this coordinate system takes the explicit form
where the coefficient K, which is of order 1, depends on the particular startup procedure adopted for the outward integration. Far from the vertex, the condition (10) on the time step Δu is quantitatively similar to the CFL condition for a standard Cauchy evolution algorithm in spherical coordinates. But condition (10) is strongest near the vertex of the cone where (at the equator θ = π/2) it implies that
This is in contrast to the analogous requirement
for stable Cauchy evolution near the origin of a spherical coordinate system. The extra power of Δθ is the price that must be paid near the vertex for the simplicity of a characteristic code. Nevertheless, the enforcement of this condition allowed efficient global simulation of axisymmetric scalar waves. Global studies of backscattering, radiative tail decay, and solitons were carried out for nonlinear axisymmetric waves [153], but three-dimensional simulations extending to the vertices of the cones were impractical at the time on existing machines.
Aware now of the subtleties of the CFL condition near the vertices, the Pittsburgh group returned to the Bondi problem, i.e. to evolve the Bondi metric [54]
by means of the three hypersurface equations
and the evolution equation
The beauty of the Bondi equations is that they form a clean hierarchy. Given γ on an initial null hypersurface, the equations can be integrated radially to determine β, U, V, and γ,u on the hypersurface (in that order) in terms of integration constants determined by boundary conditions, or smoothness conditions if extended to the vertex of a null cone. The initial data γ is unconstrained except for smoothness conditions. Because γ represents an axisymmetric spin-2 field, it must be \({\mathcal O}({\sin ^2}\theta)\) near the poles of the spherical coordinates and must consist of l ≥ 2 spin-2 multipoles.
In the computational implementation of this system by the Pittsburgh group [120], the null hypersurfaces were chosen to be complete null cones with nonsingular vertices, which (for simplicity) trace out a geodesic worldline r = 0. The smoothness conditions at the vertices were formulated in local Minkowski coordinates.
The vertices of the cones were not the chief source of difficulty. A null parallelogram marching algorithm, similar to that used in the scalar case, gave rise to another instability that sprang up throughout the grid. In order to reveal the source of this instability, physical considerations suggested looking at the linearized version of the Bondi equations, where they can be related to the wave equation. If this relationship were sufficiently simple, then the scalar wave algorithm could be used as a guide in stabilizing the evolution of γ. A scheme for relating γ to solutions Φ of the wave equation had been formulated in the original paper by Bondi, Metzner, and van der Burgh [54]. However, in that scheme, the relationship of the scalar wave to γ was nonlocal in the angular directions and was not useful for the stability analysis.
A local relationship between γ and solutions of the wave equation was found [120]. This provided a test bed for the null evolution algorithm similar to the Cauchy test bed provided by Teukolsky waves [239]. More critically, it allowed a simple von Neumann linear stability analysis of the finite difference equations, which revealed that the evolution would be unstable if the metric quantity U was evaluated on the grid. For a stable algorithm, the grid points for U must be staggered between the grid points for γ, β, and V. This unexpected feature emphasizes the value of linear stability analysis in formulating stable finite difference approximations.
It led to an axisymmetric code [186, 120] for the global Bondi problem which ran stably, subject to a CFL condition, throughout the regime in which caustics and horizons did not form. Stability in this regime was verified experimentally by running arbitrary initial data until it radiated away to \({{\mathcal I}^ +}\). Also, new exact solutions as well as the linearized null solutions were used to perform extensive convergence tests that established second order accuracy. The code generated a large complement of highly accurate numerical solutions for the class of asymptotically flat, axisymmetric vacuum spacetimes, a class for which no analytic solutions are known. All results of numerical evolutions in this regime were consistent with the theorem of Christodoulou and Klainerman [75] that weak initial data evolve asymptotically to Minkowski space at late time.
An additional global check on accuracy was performed using Bondi’s formula relating mass loss to the time integral of the square of the news function. The Bondi mass loss formula is not one of the equations used in the evolution algorithm but follows from those equations as a consequence of a global integration of the Bianchi identities. Thus it not only furnishes a valuable tool for physical interpretation but it also provides a very important calibration of numerical accuracy and consistency.
An interesting feature of the evolution arises in regard to compactification. By construction, the u-direction is timelike at the origin where it coincides with the worldline traced out by the vertices of the outgoing null cones. But even for weak fields, the u-direction generically becomes spacelike at large distances along an outgoing ray. Geometrically, this reflects the property that \({{\mathcal I}^ +}\) is itself a null hypersurface so that all internal directions are spacelike, except for the null generator. For a flat space time, the u-direction picked out at the origin leads to a null evolution direction at \({{\mathcal I}^ +}\), but this direction becomes spacelike under a slight deviation from spherical symmetry. Thus the evolution generically becomes “superluminal” near \({{\mathcal I}^ +}\). Remarkably, this leads to no adverse numerical effects. This remarkable property apparently arises from the natural way that causality is built into the marching algorithm so that no additional resort to numerical techniques, such as “causal differencing” [78], is necessary.
3.3.1 The conformal-null tetrad approach
Stewart has implemented a characteristic evolution code which handles the Bondi problem by a null tetrad, as opposed to metric, formalism [231]. The geometrical algorithm underlying the evolution scheme, as outlined in [233, 99], is Friedrich’s [94] conformal-null description of a compactified spacetime in terms of a first order system of partial differential equations. The variables include the metric, the connection, and the curvature, as in a Newman-Penrose formalism, but in addition the conformal factor (necessary for compactification of \({\mathcal I}\)) and its gradient. Without assuming any symmetry, there are more than 7 times as many variables as in a metric based null scheme, and the corresponding equations do not decompose into as clean a hierarchy. This disadvantage, compared to the metric approach, is balanced by several advantages:
-
The equations form a symmetric hyperbolic system so that standard theorems can be used to establish that the system is well-posed.
-
Standard evolution algorithms can be invoked to ensure numerical stability.
-
The extra variables associated with the curvature tensor are not completely excess baggage, since they supply essential physical information.
-
The regularization necessary to treat \({{\mathcal I}^ +}\) is built in as part of the formalism so that no special numerical regularization techniques are necessary as in the metric case. (This last advantage is somewhat offset by the necessity of having to locate \({\mathcal I}\) by tracking the zeroes of the conformal factor.)
The code was intended to study gravitational waves from an axisymmetric star. Since only the vacuum equations are evolved, the outgoing radiation from the star is represented by data (Ψ4 in Newman-Penrose notation) on an ingoing null cone forming the inner boundary of the evolved domain. This inner boundary data is supplemented by Schwarzschild data on the initial outgoing null cone, which models an initially quiescent state of the star. This provides the necessary data for a double-null initial value problem. The evolution would normally break down where the ingoing null hypersurface develops caustics. But by choosing a scenario in which a black hole is formed, it is possible to evolve the entire region exterior to the horizon. An obvious test bed is the Schwarzschild spacetime for which a numerically satisfactory evolution was achieved (although convergence tests were not reported).
Physically interesting results were obtained by choosing data corresponding to an outgoing quadrupole pulse of radiation. By increasing the initial amplitude of the data Ψ4, it was possible to evolve into a regime where the energy loss due to radiation was large enough to drive the total Bondi mass negative. Although such data is too grossly exaggerated to be consistent with an astrophysically realistic source, the formation of a negative mass was an impressive test of the robustness of the code.
3.3.2 Axisymmetric mode coupling
Papadopoulos [183] has carried out an illuminating study of mode mixing by computing the evolution of a pulse emanating outward from an initially Schwarzschild white hole of mass M. The evolution proceeds along a family of ingoing null hypersurfaces with outer boundary at r = 60 M. The evolution is stopped before the pulse hits the outer boundary in order to avoid spurious effects from reflection and the radiation is inferred from data at r = 20 M. Although gauge ambiguities arise in reading off the waveform at a finite radius, the work reveals interesting nonlinear effects: (i) modification of the light cone structure governing the principal part of the equations and hence the propagation of signals; (ii) modulation of the Schwarzschild potential by the introduction of an angular dependent “mass aspect”; and (iii) quadratic and higher order terms in the evolution equations which couple the spherical harmonic modes. A compactified version of this study [256] was later carried out with the 3D PITT code, which confirms these effects as well as new effects which are not present in the axisymmetric case (see Section 4.5 for details).
3.3.3 Spectral approach to the Bondi problem
Oliveira and Rodrigues [81] have presented the first code based upon the Galerkin spectral method to evolve the axisymmetic Bondi problem. The strength of spectral methods is to provide high accuracy relative to computational effort. The spectral decomposition reduces the partial differential evolution system to a system of ordinary differential equations for the spectral coefficients. Several numerical tests were performed to verify stability and convergence, including linearized gravitational waves and the global energy momentum conservation law relating the Bondi mass to the radiated energy flux. The main feature of the Galerkin method is that each basis function is chosen to automatically satisfy the boundary conditions, in this case the regularity conditions on the Bondi variables on the axes of symmetry and at the vertices of the outgoing null cones and the asymptotic flatness condition at infinity. Although \({{\mathcal I}^ +}\) is not explicitly compactified, the choice of radial basis functions allows verification of the asymptotic relations governing the coefficients of the leading gauge dependent terms of the metric quantities. The results promise a new approach to study spacetimes with gravitational waves. It will be interesting to see whether the approach can be generalized to the full 3D case.
3.3.4 Twisting axisymmetry
The Southampton group, as part of its goal of combining Cauchy and characteristic evolution, has developed a code [85, 86, 194] which extends the Bondi problem to full axisymmetry, as described by the general characteristic formalism of Sachs [211]. By dropping the requirement that the rotational Killing vector be twist-free, they were able to include rotational effects, including radiation in the “cross” polarization mode (only the “plus” mode is allowed by twist-free axisymmetry). The null equations and variables were recast into a suitably regularized form to allow compactification of null infinity. Regularization at the vertices or caustics of the null hypersurfaces was not necessary, since they anticipated matching to an interior Cauchy evolution across a finite worldtube.
The code was designed to insure standard Bondi coordinate conditions at infinity, so that the metric has the asymptotically Minkowskian form corresponding to null-spherical coordinates. In order to achieve this, the hypersurface equation for the Bondi metric variable β must be integrated radially inward from infinity, where the integration constant is specified. The evolution of the dynamical variables proceeds radially outward as dictated by causality [194]. This differs from the Pittsburgh code in which all the equations are integrated radially outward, so that the coordinate conditions are determined at the inner boundary and the metric is asymptotically flat but not asymptotically Minkowskian. The Southampton scheme simplifies the formulae for the Bondi news function and mass in terms of the metric. It is anticipated that the inward integration of β causes no numerical problems because this is a gauge choice which does not propagate physical information. However, the code has not yet been subject to convergence and long term stability tests so that these issues cannot be properly assessed at the present time.
The matching of the Southampton axisymmetric code to a Cauchy interior is discussed in Section 5.6.
3.4 The Bondi mass
Numerical calculations of asymptotic quantities such as the Bondi mass must pick off non-leading terms in an asymptotic expansion about infinity. This is similar to the experimental task of determining the mass of an object by measuring its far field. For example, in an asymptotically inertial Bondi frame at \({{\mathcal I}^ +}\) (in which the metric takes an asymptotically Minkowski form in null spherical coordinates)), the mass aspect \({\mathcal M}(u, \theta, \phi)\) is picked off from the asymptotic expansion of Bondi’s metric quantity V (see Equation (16)) of the form \(V = r - 2{\mathcal M} + {\mathcal O}(1/r)\). In gauges which incorporate some of the properties of an asymptotically inertial frame, such as the null quasi-spherical gauge [30] in which the angular metric is conformal to the unit sphere metric, this can be a straightforward computational problem. However, the job can be more difficult if the gauge does not correspond to a standard Bondi frame at \({{\mathcal I}^ +}\). One must then deal with an arbitrary coordinatization of \({{\mathcal I}^ +}\) which is determined by the details of the interior geometry. As a result, V has a more complicated asymptotic behavior, given in the axisymmetric case by
where L, H, and K are gauge dependent functions of (u, θ) which would vanish in an inertial Bondi frame [237, 153]. The calculation of the Bondi mass requires regularization of this expression by numerical techniques so that the coefficient \({\mathcal M}\) can be picked off. The task is now similar to the experimental determination of the mass of an object by using non-inertial instruments in a far zone which contains \({\mathcal O}(1/r)\) radiation fields. But it has been done!
It was accomplished in Stewart’s code by re-expressing the formula for the Bondi mass in terms of the well-behaved fields of the conformal formalism [231]. In the Pittsburgh code, it was accomplished by re-expressing the Bondi mass in terms of renormalized metric variables which regularize all calculations at \({{\mathcal I}^ +}\) and made them second order accurate in grid size [121]. The calculation of the Bondi news function (which provides the waveforms of both polarization modes) is an easier numerical task than the Bondi mass. It has also been implemented in both of these codes, thus allowing the important check of the Bondi mass loss formula.
An alternative approach to computing the Bondi mass is to adopt a gauge which corresponds more closely to an inertial Bondi frame at \({{\mathcal I}^ +}\) and simplifies the asymptotic limit. Such a choice is the null quasi-spherical gauge in which the angular part of the metric is proportional to the unit sphere metric, and as a result the gauge term K vanishes in Equation (18). This gauge was adopted by Bartnik and Norton at Canberra in their development of a 3D characteristic evolution code [30] (see Section 4 for further discussion). It allowed accurate computation of the Bondi mass as a limit as r → ∞ of of the Hawking mass [27].
Mainstream astrophysics is couched in Newtonian concepts, some of which have no well defined extension to general relativity. In order to provide a sound basis for relativistic astrophysics, it is crucial to develop general relativistic concepts which have well defined and useful Newtonian limits. Mass and radiation flux are fundamental in this regard. The results of characteristic codes show that the energy of a radiating system can be evaluated rigorously and accurately according to the rules for asymptotically flat spacetimes, while avoiding the deficiencies that plagued the “pre-numerical” era of relativity: (i) the use of coordinate dependent concepts such as gravitational energy-momentum pseudotensors; (ii) a rather loose notion of asymptotic flatness, particularly for radiative spacetimes; (iii) the appearance of divergent integrals; and (iv) the use of approximation formalisms, such as weak field or slow motion expansions, whose errors have not been rigorously estimated.
Characteristic codes have extended the role of the Bondi mass from that of a geometrical construct in the theory of isolated systems to that of a highly accurate computational tool. The Bondi mass loss formula provides an important global check on the preservation of the Bianchi identities. The mass loss rates themselves have important astrophysical significance. The numerical results demonstrate that computational approaches, rigorously based upon the geometrical definition of mass in general relativity, can be used to calculate radiation losses in highly nonlinear processes where perturbation calculations would not be meaningful.
Numerical calculation of the Bondi mass has been used to explore both the Newtonian and the strong field limits of general relativity [121]. For a quasi-Newtonian system of radiating dust, the numerical calculation joins smoothly on to a post-Newtonian expansion of the energy in powers of 1/c, beginning with the Newtonian mass and mechanical energy as the leading terms. This comparison with perturbation theory has been carried out to \({\mathcal O}(1/{c^7})\), at which stage the computed Bondi mass peels away from the post-Newtonian expansion. It remains strictly positive, in contrast to the truncated post-Newtonian behavior which leads to negative values.
A subtle feature of the Bondi mass stems from its role as one component of the total energy-momentum 4-vector, whose calculation requires identification of the translation subgroup of the Bondi-Metzner-Sachs group [210]. This introduces boost freedom into the problem. Identifying the translation subgroup is tantamount to knowing the conformal transformation to an inertial Bondi frame [237] in which the time slices of \({{\mathcal I}^ +}\) have unit sphere geometry. Both Stewart’s code and the Pittsburgh code adapt the coordinates to simplify the description of the interior sources. This results in a non-standard foliation of \({{\mathcal I}^ +}\). The determination of the conformal factor which relates the 2-metric hAB of a slice of \({{\mathcal I}^ +}\) to the unit sphere metric is an elliptic problem equivalent to solving the second order partial differential equation for the conformal transformation of Gaussian curvature. In the axisymmetric case, the PDE reduces to an ODE with respect to the angle θ, which is straightforward to solve [121]. The integration constants determine the boost freedom along the axis of symmetry.
The non-axisymmetric case is more complicated. Stewart [231] proposes an approach based upon the dyad decomposition
The desired conformal transformation is obtained by first relating hAB conformally to the flat metric of the complex plane. Denoting the complex coordinate of the plane by ζ, this relationship can be expressed as dζ = efmAdxA. The conformal factor f can then be determined from the integrability condition
This is equivalent to the classic Beltrami equation for finding isothermal coordinates. It would appear to be a more effective scheme than tackling the second order PDE directly, but numerical implementation has not yet been carried out.
4 3D Characteristic Evolution
The initial work on 3D characteristic evolution led to two independent codes, one developed at Canberra and the other at Pittsburgh (the PITT code), both with the capability to study gravitational waves in single black hole spacetimes at a level not yet mastered at the time by Cauchy codes. The Pittsburgh group established robust stability and second order accuracy of a fully nonlinear 3D code which was able to calculate the waveform at null infinity [49, 46] and to track a dynamical black hole and excise its internal singularity from the computational grid [119, 116]. The Canberra group implemented an independent nonlinear 3D code which accurately evolved the exterior region of a Schwarzschild black hole. Both codes pose data on an initial null hypersurface and on a worldtube boundary, and evolve the exterior spacetime out to a compactified version of null infinity, where the waveform is computed. However, there are essential differences in the underlying geometrical formalisms and numerical techniques used in the two codes and in their success in evolving generic black hole spacetimes. Recently two new codes have evolved from the PITT code by introducing a new choice of spherical coordinates [111, 201].
4.1 Coordinatization of the sphere
Any characteristic code extending to \({{\mathcal I}^ +}\) requires the ability to handle tensor fields and their derivatives on the sphere. Spherical coordinates and spherical harmonics are natural analytic tools for the description of radiation, but their implementation in computational work requires dealing with the impossibility of smoothly covering the sphere with a single coordinate grid. Polar coordinate singularities in axisymmetric systems can be regularized by standard tricks. In the absence of symmetry, these techniques do not generalize and would be especially prohibitive to develop for tensor fields.
The development of grids smoothly covering the sphere has had a long history in computational meteorology that has led to two distinct approaches: (i) the stereographic approach in which the sphere is covered by two overlapping patches obtained by stereographic projection about the North and South poles [58]; and (ii) the cubed-sphere approach in which the sphere is covered by the 6 patches obtained by a projection of the faces of a circumscribed cube [206]. A discussion of the advantages of each of these methods and a comparison of their performance in a standard fluid testbed are given in [58]. In numerical relativity, the stereographic method has been reinvented in the context of the characteristic evolution problem [180]; and the cubed-sphere method has been reinvented in building an apparent horizon finder [242]. The cubed sphere module, including the interpatch transformations, has been integrated into the Cactus toolkit and later applied to black hole excision [241]. Perhaps the most ingenious treatment of the sphere, based upon a toroidal map, was devised by the Canberra group in building their characteristic code [30]. These methods are described below.
4.1.1 Stereographic grids
Motivated by problems in meteorology, G. L. Browning, J. J. Hack and P. N. Swartztrauber [58] developed the first finite difference scheme based upon a composite mesh with two overlapping stereographic coordinate patches, each having a circular boundary centered about the North or South poles. Values for quantities required at ghost points beyond the boundary of one of the patches were interpolated from values in the other patch. Because a circular boundary does not fit regularly on a stereographic grid, dissipation was found necessary to remove the short wavelength error resulting from the inter-patch interpolations. They used the shallow water equations as a testbed to compare their approach to existing spectral approaches in terms of computer time, execution rate and accuracy. Such comparisons of different numerical methods can be difficult. Both the finite difference and spectral approaches gave good results and were competitive in terms of overall operation count and memory requirements For the particular initial data sets tested, the spectral approach had an advantage but not enough to give clear indication of the suitability of one method over another. The spectral method with M modes requires O(M3) operations per time step compared with O(N2) for a finite difference method on a N × N grid. However, assuming that the solution is smooth, the accuracy of the spectral method is O(e−M) compared to, say, O(N−6) for a sixth order finite difference method. Hence, for comparable accuracy, M = O(ln N) which implies that the operation count for the spectral and finite difference methods are O[(ln N)3] and O(N2), respectively. Thus for sufficiently high accuracy, i.e. large N, the spectral method requires fewer operations. The issue of spectral vs finite difference methods thus depends on the nature of the smoothness of the physical problem being addressed and the accuracy desired.
The Pitt null code was first developed using two stereographic patches with square boundaries, each overlapping the equator. This has recently been modified based upon the approach advocated in [58], which retains the original stereographic coordinates but shrinks the overlap region by masking a circular boundary near the equator. The original square boundaries aligned with the grid and did not require numerical dissipation. However, the corners of the square boundary, besides being a significant waste of economy, were a prime source of inaccuracy. The resolution at the corners is only 1/9th that at the poles due to the stretching of the stereographic map. Near the equator, the resolution is approximately 1/2 that at the poles. The use of a circular boundary requires an angular version of numerical dissipation to control the resulting high frequency error (see Section 4.2.1).
A crucial ingredient of the PITT code is the ð-module [118] which incorporates a computational version of the Newman-Penrose eth-formalism [180]. The underlying method can be applied to any smooth coordinatization xA of the sphere based upon several patches. The unit sphere metric qAB, defined by these coordinates, is decomposed in each patch in terms of a complex basis vector qA,
Vector and tensor fields on the sphere, and their covariant derivatives, are then represented by their basis components. For example, the vector field UA is represented by the complex spin-weight 1 field U = UAqA. The covariant derivative DA associated with qAB is then expressed in terms of the ð operator according to
The eth-calculus simplifies the underlying equations, avoids spurious coordinate singularities and allows accurate differentiation of tensor fields on the sphere in a computationally efficient and clean way. Its main weakness is the numerical noise introduced by interpolations between the patches.
4.1.2 Cubed sphere grids
C. Ronchi, R. Iacono and P. S. Paolucci [206], developed the “cubed-sphere” approach as a new gridding method for solving global meteorological problems. The method decomposes the sphere into the 6 identical regions obtained by projection of a cube circumscribed on its surface. This gives a variation of the composite mesh method in which the 6 domains butt up against each other along shared grid boundaries. As a result only 1-dimensional intergrid interpolations are necessary (as opposed to the 2-dimensional interpolations of the stereographic grid), which results in enhanced accuracy. The symmetry of the scheme, in which the six patches have the same geometric structure and grid, also allows efficient use of parallel computer architectures. Their tests of the cubed sphere method based upon the simulation of shallow water waves in spherical geometry show that the numerical solutions are as accurate as those with spectral methods, with substantial saving in execution time. Recently, the cubed-sphere method has also been developed for application to characteristic evolution in numerical relativity [201, 111]. The eth-calculus is used to treat tensor fields on the sphere in the same way as in the stereographic method except the interpatch transformations now involve 6, rather than 2, sets of basis vectors.
4.1.3 Toroidal grids
The Canberra group treats fields on the sphere by taking advantage of the existence of a smooth map from the torus to the sphere [30]. The pullback of this map allows functions on the sphere to be expressed in terms of toroidal coordinates. The intrinsic topology of these toroidal coordinates allow them to take advantage of of fast-Fourier transforms to implement a highly efficient pseudo-spectral treatment. This ingenious method has apparently not yet been adopted in other fields.
4.2 Geometrical formalism
The PITT code uses a standard Bondi-Sachs null coordinate system,
where det(hAB) = det(qAB) for some standard choice qAB of the unit sphere metric. This generalizes Equation (13) to the three-dimensional case. The characteristic version of Einstein’s equations are The hypersurface equations derive from the \({G_\mu}^\nu {\nabla _\nu}u\) components of the Einstein tensor. They take the explicit form [248]
where DA is the covariant derivative and \({\mathcal R}\) the curvature scalar of the conformal 2-metric hAB of the r = const. surfaces, and capital Latin indices are raised and lowered with hAB. Given the null data hAB on an outgoing null hypersurface, this hierarchy of equations can be integrated radially in order to determine β, UA and V on the hypersurface in terms of integration constants on an inner boundary. The evolution equations for the u-derivative of the null data derive from the trace-free part of the angular components of the Einstein tensor, i.e. the components mAmBGAB where \({h^{AB}} = 2{m^{(A}}{{\bar m}^B})\). They take the explicit form
A compactified treatment of null infinity is achieved by introducing the radial coordinate x = r/(R + r), where R is a scale parameter adjusted to the size of the inner boundary. Thus x = 1 at \({{\mathcal I}^ +}\).
The Canberra code employs a null quasi-spherical (NQS) gauge (not to be confused with the quasi-spherical approximation in which quadratically aspherical terms are ignored [49]). The NQS gauge takes advantage of the possibility of mapping the angular part of the Bondi metric conformally onto a unit sphere metric, so that hAB → qAB. The required transformation xA → yA (u, r, xA) is in general dependent upon u and r so that the NQS angular coordinates yA are not constant along the outgoing null rays, unlike the Bondi-Sachs angular coordinates. Instead the coordinates yA display the analogue of a shift on the null hypersurfaces u = const. In addition, the NQS spheres (u, r) = const. are not the same as the Bondi spheres. The radiation content of the metric is contained in a shear vector describing this shift. This results in the description of the radiation in terms of a spin-weight 1 field, rather than the spin-weight 2 field associated with hAB in the Bondi-Sachs formalism. In both the Bondi-Sachs and NQS gauges, the independent gravitational data on a null hypersurface is the conformal part of its degenerate 3-metric. The Bondi-Sachs null data consist of hAB, which determines the intrinsic conformal metric of the null hypersurface. In the NQS case, hAB = qAB and the shear vector comprises the only non-trivial part of the conformal 3-metric. Both the Bondi-Sachs and NQS gauges can be arranged to coincide in the special case of shear-free Robinson-Trautman metrics [82, 26].
The formulation of Einstein’s equations in the NQS gauge is presented in [25], and the associated gauge freedom arising from (u, r) dependent rotation and boosts of the unit sphere is discussed in [26]. As in the PITT code, the main equations involve integrating a hierarchy of hypersurface equations along the radial null geodesics extending from the inner boundary to null infinity. In the NQS gauge the source terms for these radial ODEs are rather simple when the unknowns are chosen to be the connection coefficients. However, as a price to pay for this simplicity, after the radial integrations are performed on each null hypersurface a first order elliptic equation must be solved on each r = const. cross-section to reconstruct the underlying metric.
4.2.1 Angular dissipation
For a {3 +1} evolution algorithm based upon a system of wave equations, or any other symmetric hyperbolic system, numerical dissipation can be added in the standard Kreiss-Oliger form [158]. Dissipation cannot be added to the {2 + 1 + 1} format of characteristic evolution in this standard way for {3 + 1} Cauchy evolution. In the original version of the PITT code, which used square stereographic patches with boundaries aligned with the grid, numerical dissipation was only introduced in the radial direction [163]. This was sufficient to establish numerical stability. In the new version of the code with circular stereographic patches, whose boundaries fit into the stereographic grid in an irregular way, angular dissipation is necessary to suppress the resulting high frequency error.
Angular dissipation can be introduced in the following way [14]. In terms of the spin-weight 2 variable J = qAqBhAB, the evolution equation (27) takes the form
where S represents the right hand side terms. We add angular dissipation to the u-evolution through the modification
where h is the discretization size and ϵu ≥ 0 is an adjustable parameter independent of h. This leads to
Integration over the unit sphere with solid angle element dΩ then gives
Thus the ϵu-term has the effect of damping high frequency noise as measured by the L2 norm of ∂r(rJ) over the sphere.
Similarly, dissipation can be introduced in the radial integration of (28) through the substitution
with ϵr ≥ 0. Angular dissipation can also be introduced in the hypersurface equations, e.g. in (26) through the substitution
4.2.2 First versus second differential order
The PITT code was originally formulated in the second differential form of Equations (24, 25, 26, 27), which in the spin-weighted version leads to an economical number of 2 real and 2 complex variables. Subsequently, the variable
was introduced to reduce Equation (25) to two first order radial equations, which simplified the startup procedure at the boundary. Although the resulting code was verified to be stable and second order accurate, its application to problems involving strong fields and gradients led to numerical errors which made small scale effects of astrophysical importance difficult to measure.
In particular, in initial attempts to simulate a white hole fission, Gómez [110] encountered an oscillatory error pattern in the angular directions near the time of fission. The origin of the problem was tracked to numerical error of an oscillatory nature introduced by ð2 terms in the hypersurface and evolution equations. Gómez’s solution was to remove the offending second angular derivatives by introducing additional variables and reducing the system to first differential order in the angular directions. This suppressed the oscillatory mode and subsequently improved performance in the simulation of the white hole fission problem [113] (see Section 4.4.2).
This success opens the issue of whether a completely first differential order code might perform even better, as has been proposed by Gómez and Frittelli [112]. By the use of ∂uhAB as a fundamental variable, they cast the Bondi system into Duff’s first order quasilinear canonical form [88]. At the analytic level this provides standard uniqueness and existence theorems (extending previous work for the linearized case [102]) and is a starting point for establishing the estimates required for well-posedness.
At the numerical level, Gómez and Frittelli point out that this first order formulation provides a bridge between the characteristic and Cauchy approaches which allows application of standard methods for constructing numerical algorithms, e.g. to take advantage of shock-capturing schemes. Although true shocks do not exist for vacuum gravitational fields, when coupled to hydro the resulting shocks couple back to form steep gradients which might not be captured by standard finite difference approximations. In particular, the second derivatives needed to compute gravitational radiation from stellar oscillations have been noted to be a troublesome source of inaccuracy in the characteristic treatment of hydrodynamics [220]. Application of standard versions of AMR is also facilitated by the first order form.
The benefits of this completely first order approach are not simple to decide without code comparison. The part of the code in which the ð2 operator introduced the oscillatory error mode in [110] was not identified, i.e. whether it originated in the inner boundary treatment or in the interpolations between stereographic patches where second derivatives might be troublesome. There are other possible ways to remove the oscillatory angular modes, such as adding angular dissipation (see Section 4.2.1). The finite difference algorithm in the original PITT code only introduced numerical dissipation in the radial direction [163]. The economy of variables and other advantages of a second order scheme [159] should not be abandoned without further tests and investigation.
4.2.3 Numerical methods
The PITT code is an explicit finite difference evolution algorithm based upon retarded time steps on a uniform three-dimensional null coordinate grid based upon the stereographic coordinates and a compactified radial coordinate. The straightforward numerical implementation of the finite difference equations has facilitated code development. The Canberra code uses an assortment of novel and elegant numerical methods. Most of these involve smoothing or filtering and have obvious advantage for removing short wavelength noise but would be unsuitable for modeling shocks.
There have been two recent projects, to improve the performance of the PITT code by using the cubed-sphere method to coordinatize the sphere. They both include an adaptation of the eth-calculus to handle the transformation of spin-weighted variables between the six patches.
In one of these projects, Gómez, Barreto and Frittelli develop the cubed-sphere approach into an efficient, highly parallelized 3D code, the LEO code, for the characteristic evolution of the coupled Einstein-Klein-Gordon equations in the Bondi-Sachs formalism [111]. This code was demonstrated to be convergent and its high accuracy in the linearized regime with a Schwarzschild background was demonstrated by the simulation of the quasinormal ringdown of the scalar field and its energy-momentum conservation.
Because the characteristic evolution scheme constitutes a radial integration carried out for each angle on the sphere of null directions, the natural way to parallelize the code is distribute the angular grid among processors. Thus given M × M processors one can distribute the N × N points in each spherical patch (cubed-sphere or stereographic), assigning to each processor equal square grids of extent N/M in each direction. To be effective this requires that the communication time between processors scales effectively. This depends upon the ghost point location necessary to supply nearest neighbor data and is facilitated in the cubed-sphere approach because the ghost points are aligned on 1-dimensional grid lines, whose pattern is invariant under grid size. In the stereographic approach, the ghost points are arranged in an irregular pattern which changes in an essentially random way under rescaling and requires a more complicated parallelization algorithm.
Their goal is to develop the LEO code for application to black hole-neutron star binaries in a close orbit regime where the absence of caustics make a pure characteristic evolution possible. Their first anticipated application is the simulation of a boson star orbiting a black hole, whose dynamics is described by the Einstein-Klein-Gordon equations. They point out that characteristic evolution of such systems of astrophysical interest have been limited in the past by resolution due to the lack off the necessary computational power, parallel infrastructure and mesh refinement. Most characteristic code development has been geared toward single processor machines whereas the current computational platforms are designed toward performing high resolution simulations in reasonable times by parallel processing.
At the same time the LEO code was being developed, Reisswig et al. [201] also constructed a characteristic code for the Bondi-Sachs problem based upon the cubed-sphere infrastructure of Thornburg [242, 241]. They retain the original second order differential form of the angular operators is retained.
The Canberra code handles fields on the sphere by means of a 3-fold representation: (i) as discretized functions on a spherical grid uniformly spaced in standard (θ, ϕ) coordinates, (ii) as fast-Fourier transforms with respect to (θ, ϕ) (based upon the smooth map of the torus onto the sphere), and (iii) as a spectral decomposition of scalar, vector, and tensor fields in terms of spin-weighted spherical harmonics. The grid values are used in carrying out nonlinear algebraic operations; the Fourier representation is used to calculate (θ, ϕ)-derivatives; and the spherical harmonic representation is used to solve global problems, such as the solution of the first order elliptic equation for the reconstruction of the metric, whose unique solution requires pinning down the ℓ = 1 gauge freedom. The sizes of the grid and of the Fourier and spherical harmonic representations are coordinated. In practice, the spherical harmonic expansion is carried out to 15th order in ℓ, but the resulting coefficients must then be projected into the ℓ ≤ 10 subspace in order to avoid inconsistencies between the spherical harmonic, grid, and Fourier representations.
The Canberra code solves the null hypersurface equations by combining an 8th order Runge-Kutta integration with a convolution spline to interpolate field values. The radial grid points are dynamically positioned to approximate ingoing null geodesics, a technique originally due to Goldwirth and Piran [109] to avoid the problems with a uniform r-grid near a horizon which arise from the degeneracy of an areal coordinate on a stationary horizon. The time evolution uses the method of lines with a fourth order Runge-Kutta integrator, which introduces further high frequency filtering.
4.2.4 Stability
4.2.4.1 PITT code
Analytic stability analysis of the finite difference equations has been crucial in the development of a stable evolution algorithm, subject to the standard Courant-Friedrichs-Lewy (CFL) condition for an explicit code. Linear stability analysis on Minkowski and Schwarzschild backgrounds showed that certain field variables must be represented on the half-grid [120, 49]. Nonlinear stability analysis was essential in revealing and curing a mode coupling instability that was not present in the original axisymmetric version of the code [46, 163]. This has led to a code whose stability persists even in the regime that the u-direction, along which the grid flows, becomes spacelike, such as outside the velocity of light cone in a rotating coordinate system. Severe tests were used to verify stability. In the linear regime, robust stability was established by imposing random initial data on the initial characteristic hypersurface and random constraint violating boundary data on an inner worldtube. (Robust stability was later adopted as one of the standardized tests for Cauchy codes [5].) The code ran stably for 10,000 grid crossing times under these conditions [49]. The PITT code was the first 3D general relativistic code to pass this robust stability test. The use of random data is only possible in sufficiently weak cases where terms quadratic in the field gradients are not dominant. Stability in the highly nonlinear regime was tested in two ways. Runs for a time of 60, 000 M were carried out for a moving, distorted Schwarzschild black hole (of mass M), with the marginally trapped surface at the inner boundary tracked and its interior excised from the computational grid [116, 117]. At the time, this was by far the longest simulation of a dynamic black hole. Furthermore, the scattering of a gravitational wave off a Schwarzschild black hole was successfully carried out in the extreme nonlinear regime where the backscattered Bondi news was as large as N = 400 (in dimensionless geometric units) [46], showing that the code can cope with the enormous power output N2c5/G ≈ 1060 W in conventional units. This exceeds the power that would be produced if, in 1 second, the entire galaxy were converted to gravitational radiation.
4.2.4.2 Cubed-sphere codes
The characteristic codes using the cubed-sphere grid [111, 201] are based upon the same variables and equations as the PITT code, with the same radial integration scheme. Thus it should be expected that stability be maintained since the main difference is that the interpatch interpolations are simpler, i.e. only 1-dimensional. This appears to be the case in the reported tests, although robust stability was not directly confirmed. In particular, the LEO code showed no sign of instability in long time, high resolution simulations of the quasinormal ringdown of a scalar field scattering off a Schwarzschild black hole. Angular dissipation was not necessary
4.2.4.3 Canberra code
Analytic stability analysis of the underlying finite difference equations is impractical because of the extensive mix of spectral techniques, higher order methods, and splines. Although there is no clear-cut CFL limit on the code, stability tests show that there is a limit on the time step. The damping of high frequency modes due to the implicit filtering would be expected to suppress numerical instability, but the stability of the Canberra code is nevertheless subject to two qualifications [28, 29, 30]: (i) At late times (less than 100 M), the evolution terminates as it approaches an event horizon, apparently because of a breakdown of the NQS gauge condition, although an analysis of how and why this should occur has not yet been given. (ii) Numerical instabilities arise from dynamic inner boundary conditions and restrict the inner boundary to a fixed Schwarzschild horizon. Tests in the extreme nonlinear regime were not reported.
4.2.5 Accuracy
4.2.5.1 PITT code
The designed second order accuracy has been verified in an extensive number of testbeds [49, 46, 116, 255, 256], including new exact solutions specifically constructed in null coordinates for the purpose of convergence tests:
-
Linearized waves on a Minkowski background in null cone coordinates.
-
Boost and rotation symmetric solutions [37].
-
Schwarzschild in rotating coordinates.
-
Polarization symmetry of nonlinear twist-free axisymmetric waveforms.
-
Robinson-Trautman waveforms from perturbed Schwarzschild black holes.
-
Nonlinear Robinson-Trautman waveforms utilizing an independently computed solution of the Robinson-Trautman equation.
-
Perturbations of a Schwarzschild black hole utilizing an independently computed solution of the Teukolsky equation.
In addition to these testbeds, a set of linearized solutions has recently been obtained in the Bondi-Sachs gauge for either Schwarzschild or Minkowski backgrounds [40]. The solutions are generated by the introduction of a thin shell of matter whose density varies with time and angle. This gives rise to an exterior field containing gravitational waves. For a Minkowski background, the solution is given in exact analytic form and, for a Schwarzschild background, in terms of a power series. The solutions are parametrized by frequency and spherical harmonic decomposition. They supply a new and very useful testbed for the calibration and further development of characteristic evolution codes for Einstein’s equations, analogous to the role of the Teukolsky waves in Cauchy evolution. The PITT code showed clean second order convergence in both the L2 and L∞ error norms in tests based upon waves in a Minkowski background.
4.2.5.2 Cubed-sphere codes
Convergence of the cubed-sphere code developed by Reisswig et al [201] was also checked using linearized waves in a Minkowski background. The convergence rate for the L2 error norm was approximately second order accurate but in some cases there was significant degradation. They conjectured that the underlying source of error arises at the corners of the six patches. Comparison with the L∞ error norm would discriminate such a localized source of error but such results were not reported.
The designed convergence rate of the ð operator used in the LEO code was verified for second, fourth and eighth order finite difference approximations, using the spin-weight 2 spherical harmonic 2Y43 as a test. Similarly, the convergence of the integral relations governing the orthonormality of the spin-weighted harmonics was verified. The code includes coupling to a Klein-Gordon scalar field. Although convergence of the evolution code was not explicitly checked, high accuracy in the linearized regime with Schwarzschild background was demonstrated in the simulation of quasinormal ringdown of the scalar field and in the energy-momentum conservation of the scalar field.
4.2.5.3 Canberra code
The complexity of the algorithm and NQS gauge makes it problematic to establish accuracy by direct means. Exact solutions do not provide an effective convergence check, because the Schwarzschild solution is trivial in the NQS gauge and other known solutions in this gauge require dynamic inner boundary conditions which destabilize the present version of the code. Convergence to linearized solutions is a possible check but has not yet been performed. Instead indirect tests by means of geometric consistency and partial convergence tests are used to calibrate accuracy. The consistency tests were based on the constraint equations, which are not enforced during null evolution except at the inner boundary. The balance between mass loss and radiation flux through \({{\mathcal I}^ +}\) is a global consequence of these constraints. No appreciable growth of the constraints was noticeable until within 5 M of the final breakdown of the code. In weak field tests where angular resolution does not dominate the error, partial convergence tests based upon varying the radial grid size verify the 8th order convergence in the shear expected from the Runge-Kutta integration and splines. When the radial source of error is small, reduced error with smaller time step can also be discerned.
In practical runs, the major source of inaccuracy is the spherical harmonic resolution, which was restricted to ℓ ≤ 15 by hardware limitations. Truncation of the spherical harmonic expansion has the effect of modifying the equations to a system for which the constraints are no longer satisfied. The relative error in the constraints is 10−3 for strong field simulations [27].
4.2.6 Nonlinear scattering off a Schwarzschild black hole
A natural physical application of a characteristic evolution code is the nonlinear version of the classic problem of scattering off a Schwarzschild black hole, first solved perturbatively by Price [198]. Here the inner worldtube for the characteristic initial value problem consists of the ingoing branch of the r = 2m hypersurface (the past horizon), where Schwarzschild data are prescribed. The nonlinear problem of a gravitational wave scattering off a Schwarzschild black hole is then posed in terms of data on an outgoing null cone which describe an incoming pulse with compact support. Part of the energy of this pulse falls into the black hole and part is backscattered to \({{\mathcal I}^ +}\). This problem has been investigated using both the PITT and Canberra codes.
The Pittsburgh group studied the backscattered waveform (described by the Bondi news function) as a function of incoming pulse amplitude. The computational eth-module smoothly handled the complicated time dependent transformation between the non-inertial computational frame at \({{\mathcal I}^ +}\) and the inertial (Bondi) frame necessary to obtain the standard “plus” and “cross” polarization modes. In the perturbative regime, the news corresponds to the backscattering of the incoming pulse off the effective Schwarzschild potential. When the energy of the pulse is no larger than the central Schwarzschild mass, the backscattered waveform still depends roughly linearly on the amplitude of the incoming pulse. However, for very high amplitudes the waveform behaves quite differently. Its amplitude is greater than that predicted by linear scaling and its shape drastically changes and exhibits extra oscillations. In this very high amplitude case, the mass of the system is completely dominated by the incoming pulse, which essentially backscatters off itself in a nonlinear way.
The Canberra code was used to study the change in Bondi mass due to the radiation [27]. The Hawking mass MH(u, r) was calculated as a function of radius and retarded time, with the Bondi mass MB(u) then obtained by taking the limit r → ∞. The limit had good numerical behavior. For a strong initial pulse with ℓ = 4 angular dependence, in a run from u = 0 to u = 70 (in units where the interior Schwarzschild mass is 1), the Bondi mass dropped from 1.8 to 1.00002, showing that almost half of the initial energy of the system was backscattered and that a surprisingly negligible amount of energy fell into the black hole. A possible explanation is that the truncation of the spherical harmonic expansion cuts off wavelengths small enough to effectively penetrate the horizon. The Bondi mass decreased monotonically in time, as necessary theoretically, but its rate of change exhibited an interesting pulsing behavior whose time scale could not be obviously explained in terms of quasinormal oscillations. The Bondi mass loss formula was confirmed with relative error of less than 10−3. This is impressive accuracy considering the potential sources of numerical error introduced by taking the limit of the Hawking mass with limited resolution. The code was also used to study the appearance of logarithmic terms in the asymptotic expansion of the Weyl tensor [31]. In addition, the Canberra group studied the effect of the initial pulse amplitude on the waveform of the backscattered radiation, but did not extend their study to the very high amplitude regime in which qualitatively interesting nonlinear effects occur.
4.2.7 Black hole in a box
The PITT code has also been implemented to evolve along an advanced time foliation by ingoing null cones, with data given on a worldtube at their outer boundary and on the initial ingoing null cone. The code was used to evolve a black hole in the region interior to the worldtube by implementing a horizon finder to locate the marginally trapped surface (MTS) on the ingoing cones and excising its singular interior [119]. The code tracks the motion of the MTS and measures its area during the evolution. It was used to simulate a distorted “black hole in a box” [116]. Data at the outer worldtube was induced from a Schwarzschild or Kerr spacetime but the worldtube was allowed to move relative to the stationary trajectories; i.e. with respect to the grid the worldtube is fixed but the black hole moves inside it. The initial null data consisted of a pulse of radiation which subsequently travels outward to the worldtube where it reflects back toward the black hole. The approach of the system to equilibrium was monitored by the area of the MTS, which also equals its Hawking mass. When the worldtube is stationary (static or rotating in place), the distorted black hole inside evolved to equilibrium with the boundary. A boost or other motion of the worldtube with respect to the black hole did not affect this result. The marginally trapped surface always reached equilibrium with the outer boundary, confirming that the motion of the boundary was “pure gauge”.
This was the first code that ran “forever” in a dynamic black hole simulation, even when the worldtube wobbled with respect to the black hole to produce artificial periodic time dependence. An initially distorted, wobbling black hole was evolved for a time of 60,000 M, longer by orders of magnitude than permitted by the stability of other existing 3D black hole codes at the time. This exceptional performance opens a promising new approach to handle the inner boundary condition for Cauchy evolution of black holes by the matching methods reviewed in Section 5.
Note that setting the pulse to zero is equivalent to prescribing shear free data on the initial null cone. Combined with Schwarzschild boundary data on the outer worldtube, this would be complete data for a Schwarzschild space time. However, the evolution of such shear free null data combined with Kerr boundary data would have an initial transient phase before settling down to a Kerr black hole. This is because the twist of the shear-free Kerr null congruence implies that Kerr data specified on a null hypersurface are not generally shear free. The event horizon is an exception but Kerr null data on other null hypersurfaces have not been cast in explicit analytic form. This makes the Kerr spacetime an awkward testbed for characteristic codes. (Curiously, Kerr data on a null hypersurface with a conical type singularity do take a simple analytic form, although unsuitable for numerical evolution [90].) Using some intermediate analytic results of Israel and Pretorius [196], Venter and Bishop [50] have recently constructed a numerical algorithm for transforming the Kerr solution into Bondi coordinates and in that way provide the necessary null data numerically.
4.3 Characteristic treatment of binary black holes An important application of characteristic evolution is the calculation of the waveform emitted by binary black holes, which is possible during the very interesting nonlinear domain from merger to ringdown [165, 251]. The evolution is carried out along a family of ingoing null hypersurfaces which intersect the horizon in topological spheres. It is restricted to the period following the merger, for otherwise the ingoing null hypersurfaces would intersect the horizon in disjoint pieces corresponding to the individual black holes. The evolution proceeds backward in time on an ingoing null foliation to determine the exterior spacetime in the post-merger era. It is an example of the characteristic initial value problem posed on an intersecting pair of null hypersurfaces [212, 136], for which existence theorems apply in some neighborhood of the initial null hypersurfaces [176, 95, 94]. Here one of the null hypersurfaces is the event horizon \({{\mathcal H}^ +}\) of the binary black holes. The other is an ingoing null hypersurface J+ which intersects \({{\mathcal H}^ +}\) in a topologically spherical surface \({{\mathcal S}^ +}\) approximating the equilibrium of the final Kerr black hole, so that J+ approximates future null infinity \({{\mathcal I}^ +}\). The required data for the analytic problem consists of the degenerate conformal null metrics of \({{\mathcal H}^ +}\) and J+ and the metric and extrinsic curvature of their intersection \({{\mathcal S}^ +}\).
The conformal metric of \({{\mathcal H}^ +}\) is provided by the conformal horizon model for a binary black hole horizon [165, 150], which treats the horizon in stand-alone fashion as a three-dimensional manifold endowed with a degenerate metric γab and affine parameter t along its null rays. The metric is obtained from the conformal mapping \({\gamma _{ab}} = {\Omega ^2}{{\hat \gamma}_{ab}}\) of the intrinsic metric \({{\hat \gamma}_{ab}}\) of a flat space null hypersurface emanating from a convex surface \({{\mathcal S}_0}\) embedded at constant time in Minkowski space. The horizon is identified with the null hypersurface formed by the inner branch of the boundary of the past of \({{\mathcal S}_0}\), and its extension into the future. The flat space null hypersurface expands forever as its affine parameter \({\hat t}\) (Minkowski time) increases, but the conformal factor is chosen to stop the expansion so that the cross-sectional area of the black hole approaches a finite limit in the future. At the same time, the Raychaudhuri equation (which governs the growth of surface area) forces a nonlinear relation between the affine parameters t and \({\hat t}\). This is what produces the nontrivial topology of the affine t-slices of the black hole horizon. The relative distortion between the affine parameters t and \({\hat t}\), brought about by curved space focusing, gives rise to the trousers shape of a binary black hole horizon.
An embedding diagram of the horizon for an axisymmetric head-on collision, obtained by choosing \({{\mathcal S}_0}\) to be a prolate spheroid, is shown in Figure 3 [165]. The black hole event horizon associated with a triaxial ellipsoid reveals new features not seen in the degenerate case of the head-on collision [150], as depicted in Figure 4. If the degeneracy is slightly broken, the individual black holes form with spherical topology but as they approach, an effective tidal distortion produces two sharp pincers on each black hole just prior to merger. At merger, the two pincers join to form a single temporarily toroidal black hole. The inner hole of the torus subsequently closes up to produce first a peanut shaped black hole and finally a spherical black hole. No violation of topological censorship [93] occurs because the hole in the torus closes up superluminally. Consequently, a causal curve passing through the torus at a given time can be slipped below the bottom of a trouser leg to yield a causal curve lying entirely outside the hole [217]. In the degenerate axisymmetric limit, the pincers reduce to a point so that the individual holes have teardrop shape and they merge without a toroidal phase. Animations of this merger can be viewed at [166].
The conformal horizon model determines the data on \({{\mathcal H}^ +}\) and \({{\mathcal S}^ +}\). The remaining data necessary to evolve the exterior spacetime are given by the conformal geometry of J+, which constitutes the outgoing radiation waveform. The determination of the merger-ringdown waveform proceeds in two stages. In the first stage, this outgoing waveform is set to zero and the spacetime is evolved backward in time to calculate the incoming radiation entering from \({{\mathcal I}^ -}\). (This incoming radiation is eventually absorbed by the black hole.) From a time reversed point of view, this evolution describes the outgoing waveform emitted in the fission of a white hole, with the physically correct initial condition of no ingoing radiation. Preliminary calculations show that at late times the waveform is entirely quadrupolar (ℓ = 2) but that a strong octopole mode (ℓ = 4) exists just before fission. In the second stage of the calculation, this waveform could be used to generate the physically correct outgoing waveform for a black hole merger. The passage from the first stage to the second is the nonlinear equivalent of first determining an inhomogeneous solution to a linear problem and then adding the appropriate homogeneous solution to satisfy the boundary conditions. In this context, the first stage supplies an advanced solution and the second stage the homogeneous retarded minus advanced solution. When the evolution is carried out in the perturbative regime of a Kerr or Schwarzschild background, as in the close approximation [199], this superposition of solutions is simplified by the time reflection symmetry [251]. The second stage has been carried out in the perturbative regime of the close approximation using a characteristic code which solves the Teukolsky equation, as described in Section 4.4. More generally, beyond the perturbative regime, the merger-ringdown waveform must be obtained by a more complicated inverse scattering procedure, which has not yet been attempted.
There is a complication in applying the PITT code to this double null evolution because a dynamic horizon does not lie precisely on r-grid points. As a result, the r-derivative of the null data, i.e. the ingoing shear of \({\mathcal H}\), must also be provided in order to initiate the radial hypersurface integrations. The ingoing shear is part of the free data specified at \({{\mathcal S}^ +}\). Its value on \({\mathcal H}\) can be determined by integrating (backward in time) a sequence of propagation equations involving the horizon’s twist and ingoing divergence. A horizon code which carries out these integrations has been tested to give accurate data even beyond the merger [114].
The code has revealed new global properties of the head-on collision by studying a sequence of data for a family of colliding black holes which approaches a single Schwarzschild black hole. The resulting perturbed Schwarzschild horizon provides global insight into the close limit [199], in which the individual black holes have joined in the infinite past. A marginally anti-trapped surface divides the horizon into interior and exterior regions, analogous to the division of the Schwarzschild horizon by the r = 2M bifurcation sphere. In passing from the perturbative to the strongly nonlinear regime there is a rapid transition in which the individual black holes move into the exterior portion of the horizon. The data pave the way for the PITT code to calculate whether this dramatic time dependence of the horizon produces an equally dramatic waveform. See Section 4.4.2 for first stage results.
4.4 Perturbations of Schwarzschild
The nonlinear 3D PITT code has been calibrated in the regime of small perturbations of a Schwarzschild spacetime [255, 256] by measuring convergence with respect to independent solutions of the Teukolsky equation [238]. By decomposition into spherical harmonics, the Teukolsky equation reduces the problem of a perturbation of a stationary black hole to a 1D problem in the (t, r) subspace perturbations for a component of the Weyl tensor. Historically, the Teukolsky equation was first solved numerically by Cauchy evolution. Campanelli, Gómez, Husa, Winicour, and Zlochower [65, 151] have reformulated the Teukolsky formalism as a double-null characteristic evolution algorithm. The evolution proceeds on a family of outgoing null hypersurfaces with an ingoing null hypersurface as inner boundary and with the outer boundary compactified at future null infinity. It applies to either the Weyl component Ψ0 or Ψ4, as classified in the Newman-Penrose formalism. The Ψ0 component comprises constraint-free gravitational data on an outgoing null hypersurface and Ψ4 comprises the corresponding data on an ingoing null hypersurface. In the study of perturbations of a Schwarzschild black hole, Ψ0 is prescribed on an outgoing null hypersurface \({{\mathcal J}^ -}\), representing an early retarded time approximating past null infinity, and Ψ4 is prescribed on the inner white hole horizon \({{\mathcal H}^ -}\).
The physical setup is described in Figure 5. The outgoing null hypersurfaces extend to future null infinity \({{\mathcal I}^ +}\) on a compactified numerical grid. Consequently, there is no need for either an artificial outer boundary condition or an interior extraction worldtube. The outgoing radiation is computed in the coordinates of an observer in an inertial frame at infinity, thus avoiding any gauge ambiguity in the waveform.
The physical setup for the scattering problem. A star of mass M has undergone spherically symmetric collapse to form a black hole. The ingoing null worldtube \({\mathcal N}\) lies outside the collapsing matter. Inside \({\mathcal N}\) (but outside the matter) there is a vacuum Schwarzschild metric. Outside of \({\mathcal N}\), data for an ingoing pulse is specified on the initial outgoing null hypersurface \({{\mathcal J}^ -}\). As the pulse propagates to the black hole event horizon \({{\mathcal H}^ +}\), part of its energy is scattered to \({{\mathcal I}^ +}\).
The first calculations were carried out with nonzero data for Ψ4 on \({{\mathcal H}^ -}\) and zero data on \({{\mathcal J}^ -}\) [65] (so that no ingoing radiation entered the system). The resulting simulations were highly accurate and tracked the quasi-normal ringdown of a perturbation consisting of a compact pulse through 10 orders of magnitude and tracked the final power law decay through an additional 6 orders of magnitude. The measured exponent of the power law decay varied from ≈ 5.8, at the beginning of the tail, to ≈ 5.9 near the end, in good agreement with the predicted value of 2ℓ + 2 = 6 for a quadrupole wave [198].
The accuracy of the perturbative solutions provide a virtual exact solution for carrying out convergence tests of the nonlinear PITT null code. In this way, the error in the Bondi news function computed by the PITT code was calibrated for perturbative data consisting of either an outgoing pulse on \({{\mathcal H}^ -}\) or an ingoing pulse on \({{\mathcal J}^ -}\). For the outgoing pulse, clean second order convergence was confirmed until late times in the evolution, when small deviations from second order arise from accumulation of roundoff and truncation error. For the Bondi news produced by the scattering of an ingoing pulse, clean second order convergence was again confirmed until late times when the pulse approached the r = 2M black hole horizon. The late time error arises from loss of resolution of the pulse (in the radial direction) resulting from the properties of the compactified radial coordinate used in the code. This type of error could be eliminated by using characteristic the AMR techniques under development [197].
4.4.1 Close approximation white hole and black hole waveforms
The characteristic Teukolsky code has been used to study radiation from axisymmetric white holes and black holes in the close approximation. The radiation from an axisymmetric fissioning white hole [65] was computed using the Weyl data on \({{\mathcal H}^ -}\) supplied by the conformal horizon model described in Section 4.3, with the fission occurring along the axis of symmetry. The close approximation implies that the fission takes place far in the future, i.e. in the region of \({{\mathcal H}^ -}\) above the black hole horizon \({{\mathcal H}^ +}\). The data have a free parameter η which controls the energy yielded by the white hole fission. The radiation waveform reveals an interesting dependence on the parameter η. In the large η limit, the waveform consists of a single pulse, followed by ringdown and tail decay. The amplitude of the pulse scales quadratically with η and the width decreases with η. As η is reduced, the initial pulse broadens and develops more structure. In the small η limit, the amplitude scales linearly with η and the shape is independent of η.
Since there was no incoming radiation, the above model gave the physically appropriate boundary conditions for a white hole fission (in the close approximation). From a time reversed view point, the system corresponds to a black hole merger with no outgoing radiation at future null infinity, i.e. the analog of an advanced solution with only ingoing but no outgoing radiation. In the axisymmetric case studied, the merger corresponds to a head-on collision between two black holes. The physically appropriate boundary conditions for a black hole merger correspond to no ingoing radiation on \({{\mathcal J}^ -}\) and binary black hole data on \({{\mathcal H}^ +}\). Because \({{\mathcal J}^ -}\) and \({{\mathcal H}^ +}\) are disjoint, the corresponding data cannot be used directly to formulate a double null characteristic initial value problem. However, the ingoing radiation at \({{\mathcal J}^ -}\) supplied by the advanced solution for the black hole merger could be used as Stage I of a two stage approach to determine the corresponding retarded solution. In Stage II, this ingoing radiation is used to generate the analogue of an advanced minus retarded solution. A pure retarded solution (with no ingoing radiation but outgoing radiation at \({{\mathcal I}^ +}\) can then be constructed by superposition. The time reflection symmetry of the Schwarzschild background is key to carrying out this construction.
This two stage strategy has been carried out by Husa, Zlochower, Gómez, and Winicour [151]. The superposition of the Stage I and II solutions removes the ingoing radiation from \({{\mathcal J}^ -}\) while modifying the close approximation perturbation of \({{\mathcal H}^ +}\), essentially making it ring. The amplitude of the radiation waveform at \({{\mathcal I}^ +}\) has a linear dependence on the parameter η, which in this black hole scenario governs the energy lost in the inelastic merger process. Unlike the fission waveforms, there is very little η-dependence in their shape and the amplitude continues to scale linearly even for large η. It is not surprising that the retarded waveforms from a black hole merger differs markedly from the retarded waveforms from a white hole merger. The white hole process is directly visible at \({{\mathcal I}^ +}\) whereas the merger waveform results indirectly from the black holes through the preceding collapse of matter or gravitational energy that formed them. This explains why the fission waveform is more sensitive to the parameter η which controls the shape and timescale of the horizon data. However, the weakness of the dependence of the merger waveform on η is surprising and has potential importance for enabling the design of an efficient template for extracting a gravitational wave signal from noise.
4.4.2 Fissioning white hole
In the purely vacuum approach to the binary black hole problem, the stars which collapse to form the black holes are replaced either by imploding gravitational waves or some past singularity as in the Kruskal picture. This avoids hydrodynamic difficulties at the expense of a globally complicated initial value problem. The imploding waves either emanate from a past singularity, in which case the time-reversed application of cosmic censorship implies the existence of an anti-trapped surface; or they emanate from \({{\mathcal I}^ -}\), which complicates the issue of gravitational radiation content in the initial data and its effect on the outgoing waveform. These complications are avoided in the two stage approach adopted in the close approximation studies described in Section 4.4.1, where advanced and retarded solutions in a Schwarzschild background can be rigorously identified and superimposed. Computational experiments have been carried out to study the applicability of this approach in the nonlinear regime [113].
From a time reversed viewpoint, the first stage is equivalent to the determination of the outgoing radiation from a fission of a white hole in the absence of ingoing radiation, i.e. the physically appropriate “retarded” waveform from a white hole fission. This fission problem can be formulated in terms of data on the white hole horizon \({{\mathcal H}^ -}\) and data representing the absence of ingoing radiation on a null hypersurface J− which emanates from \({{\mathcal H}^ -}\) at an early time. The data on \({{\mathcal H}^ -}\) is provided by the conformal horizon model for a fissioning white hole. This allows study of a range of models extending from the perturbative close approximation regime, in which the fission occurs inside a black hole event horizon, to the nonlinear regime of a “bare” fission visible from \({{\mathcal I}^ +}\). The study concentrates on the axisymmetric spinless fission (corresponding in the time reversed view to the head-on collision of non-spinning black holes). In the perturbative regime, the news function agrees with the close approximation waveforms. In the highly nonlinear regime, a bare fission was found to produce a dramatically sharp radiation pulse, which then undergoes a damped oscillation. Because the black hole fission is visible from \({{\mathcal I}^ +}\), it is a more efficient source of gravitational waves than a black hole merger and can produce a higher fractional mass loss!
4.5 Nonlinear mode coupling
The PITT code has been used to model the nonlinear generation of waveforms by scattering off a Schwarzschild black hole [255, 256]. The physical setup is similar to the perturbative study in Section 4.4. A radially compact pulse is prescribed on an early time outgoing null hypersurface \({{\mathcal J}^ -}\) and Schwarzschild null data is given on the interior white hole horizon \({{\mathcal H}^ -}\), which is causally unaffected by the pulse. The input pulse is standardized to (ℓ = 2, m = 0) and (ℓ = 2, m = 2) quadrupole modes with amplitude A. The outgoing null hypersurfaces extend to future null infinity \({{\mathcal I}^ +}\) on a compactified numerical grid. Consequently, there is no need for an artificial outer boundary. The evolution code then provides the news function at \({{\mathcal I}^ +}\), in the coordinates of an observer in an inertial frame at infinity, thus avoiding any gauge ambiguity in the waveform. This provides a simple setting for how the nonlinearities generated by high amplitudes affect the waveform.
The study reveals several features of qualitative importance:
-
1.
The mode coupling amplitudes consistently scale as powers An of the input amplitude A corresponding to the nonlinear order of the terms in the evolution equations which produce the mode. This allows much economy in producing a waveform catalog: Given the order n associated with a given mode generation, the response to any input amplitude A can be obtained from the response to a single reference amplitude.
-
2.
The frequency response has similar behavior but in a less consistent way. The dominant frequencies produced by mode coupling are in the approximate range of the quasinormal frequency of the input mode and the expected sums and difference frequencies generated by the order of nonlinearity.
-
3.
Large phase shifts, ranging up 15% in a half cycle relative to the linearized waveform, are exhibited in the news function obtained by the superposition of all output modes, i.e. in the waveform of observational significance. These phase shifts, which are important for design of signal extraction templates, arise in an erratic way from superposing modes with different oscillation frequencies. This furnishes a strong argument for going beyond the linearized approximation in designing a waveform catalog for signal extraction.
-
4.
Besides the nonlinear generation of harmonic modes absent in the initial data, there is also a stronger than linear generation of gravitational wave output. This provides a potential mechanism for enhancing the strength of the gravitational radiation produced during, say, the merger phase of a binary inspiral above the strength predicted in linearized theory.
-
5.
In the non-axisymmetric m = 2 case, there is also considerable generation of radiation in polarization states not present in the linearized approximation. In the simulations, input amplitudes in the range A = 0.1 to A = 0.36 lead to nonlinear generation of the ⊕ polarization mode which is of the same order of magnitude as the ⊗ mode (which would be the sole polarization in the linearized regime). As a result, significant nonlinear amplification and phase shifting of the waveform would be observed by a gravitational wave detector, depending on its orientation.
These effects arise from the nonlinear modification of the Schwarzschild geometry identified by Papadopoulos in his prior work on axisymmetric mode coupling [183], reported in Section 3.3.2. Although Papadopoulos studied nonlinear mode generation produced by an outgoing pulse, as opposed to the case of an ingoing pulse studied in [255, 256], the same nonlinear factors were in play and gave rise to several common features. In both cases, the major effects arise in the region near r = 3M. Analogs of Features 1, 2, 3, and 4 above are all apparent in Papadopoulos’s work. At the finite difference level, both codes respect the reflection symmetry inherent in Einstein’s equations and exhibit the corresponding selection rules arising from parity considerations. In the axisymmetric case considered by Papadopoulos, this forbids the nonlinear generation of a ⊕ mode from a ⊗ mode, as described in Feature 5 above.
The evolution along ingoing null hypersurfaces in the axisymmetric work of Papadopoulos has complementary numerical features with the evolution along outgoing null hypersurfaces in the 3D work. The grid based upon ingoing null hypersurfaces avoids the difficulty in resolving effects close to r = 2M encountered with the grid based upon outgoing null hypersurfaces. The outgoing code would require AMR in order to resolve the quasinormal ringdown for as many cycles as achieved by Papadopoulos. However, the outgoing code avoids the late time caustic formation noted in Papadopoulos’ work, as well as the complications of gauge ambiguity and backscattering introduced by a finite outer boundary. One attractive option would be to combine the best features of these approaches by matching an interior evolution based upon ingoing null hypersurfaces to an exterior evolution based upon outgoing null hypersurfaces, as implemented in [164] for spherically symmetric Einstein-Klein-Gordon waves.
The waveform of relevance to gravitational wave astronomy is the superposition of modes with different frequency compositions and angular dependence. Although this waveform results from a complicated nonlinear processing of the input signal, which varies with choice of observation angle, the response of the individual modes to an input signal of arbitrary amplitude can be obtained by scaling the response to an input of standard reference amplitude. This offers an economical approach to preparing a waveform catalog.
4.6 3D Einstein-Klein-Gordon system
The Einstein-Klein-Gordon (EKG) system can be used to simulate many interesting physical phenomena. In 1D, characteristic EKG codes have been used to simulate critical phenomena and the perturbation of black holes (see Section 3.1), and a Cauchy EKG code has been used to study boson star dynamics [216]. Extending these codes to 3D would open up a new range of possibilities, e.g., the possibility to study radiation from a boson star orbiting a black hole. A first step in that direction has been achieved with the construction of a 3D characteristic code by incorporating a massless scalar field into the PITT code [22]. Since the scalar and gravitational evolution equations have the same basic form, the same evolution algorithm could be utilized. The code was tested to be second order convergent and stable. It was applied to the fully nonlinear simulation of an asymmetric pulse of ingoing scalar radiation propagating toward a Schwarzschild black hole. The resulting scalar radiation and gravitational news backscattered to \({{\mathcal I}^ +}\) was computed. The amplitudes of the scalar and gravitational radiation modes exhibited the expected power law scaling with respect to the initial pulse amplitude. In addition, the computed ringdown frequencies agreed with the results from perturbative quasinormal mode calculations.
The LEO code [111] developed by Gómez et al. has been applied to the characteristic evolution of the coupled Einstein-Klein-Gordon fields, using the cubed-sphere coordinates. The long term plan is to simulate a boson star orbiting a black hole. In simulations of a scalar pulse incident on a Schwarzschild black hole, they find the interesting result that scalar energy flow into the black hole reaches a maximum at spherical harmonic index ℓ = 2, and then decreases for larger ℓ due to the centrifugal barrier preventing the harmonics from effective penetration. The efficient parallelization allows them to perform large simulations with resolution never achieved before. Characteristic evolution of such systems of astrophysical interest have been limited in the past by resolution. They note that at the finest resolution considered in [48], it would take 1.5 months on the fastest current (single) processor to track a star in close orbit around a black hole. This is so even though the grid in question is only 81 × 123 points, which is moderate by today’s standards.
5 Cauchy-Characteristic Matching
Characteristic evolution has many advantages over Cauchy evolution. Its main disadvantage is the existence of either a caustic, where neighboring characteristics focus, or a milder version consisting of a crossover between two distinct characteristics. The vertex of a light cone is a highly symmetric caustic which already strongly limits the time step for characteristic evolution because of the CFL condition (11). It does not appear possible for a single characteristic coordinate system to cover the entire exterior region of a binary black hole spacetime without developing very complicated caustics and crossovers. This limits the waveform determined by a purely characteristic evolution to the post merger period.
CCM is a way to avoid this limitation by combining the strong points of characteristic and Cauchy evolution into a global evolution [39]. One of the prime goals of computational relativity is the simulation of the inspiral and merger of binary black holes. Given the appropriate data on a worldtube surrounding a binary system, characteristic evolution can supply the exterior spacetime and the radiated waveform. But determination of the worldtube data for a binary requires an interior Cauchy evolution. CCM is designed to solve such global problems. The potential advantages of CCM over traditional boundary conditions are
-
accurate waveform and polarization state at infinity,
-
computational efficiency for radiation problems in terms of both the grid domain and the computational algorithm,
-
elimination of an artificial outer boundary condition on the Cauchy problem, which eliminates contamination from back-reflection and clarifies the global initial value problem, and
-
a global picture of the spacetime exterior to the event horizon.
These advantages have been realized in model tests (see Sections 5.5–5.8), but CCM has not yet been achieved in fully nonlinear 3-dimensional general relativity. The early attempts to implement CCM in general relativity involved the Arnowitt-Deser-Misner (ADM) [12] formulation for the Cauchy evolution. The major problem was later traced to a pathology in the way boundary conditions have traditionally been applied in ADM codes. Exponentially growing instabilities introduced at boundaries have emerged as a major problem common to all ADM code development.
Linearized studies [234, 235, 15] of ADM evolution-boundary algorithms with prescribed values of lapse and shift show the following:
-
On analytic grounds, those ADM boundary algorithms which supply values for all components of the metric (or extrinsic curvature) are inconsistent.
-
A consistent boundary algorithm allows free specification of the transverse-traceless components of the metric with respect to the boundary.
-
Using such a boundary algorithm, linearized ADM evolution can be carried out in a bounded domain for thousands of crossing times without sign of an exponential growing instability but with error that grows secularly in time.
The linearized evolution satisfied the original criterion for robust stability that there be no exponential growth when the initial Cauchy data and free boundary data are prescribed as random numbers (in the linearized regime) [235]. However, it was subsequently shown that ADM is only weakly hyperbolic so that in the linear regime there are instabilities which grow as a power law in time. In the nonlinear regime, it is symptomatic of weakly hyperbolic systems that such secular instabilities become exponential. This has led to refined criteria for robust stability as a standardized test [15].
CCM cannot work unless the Cauchy and characteristic codes have robustly stable boundaries. This is necessarily so because interpolations continually introduce short wavelength noise into the neighborhood of the boundary. It has been demonstrated that the PITT characteristic code has a robustly stable boundary (see Section 4.2.4), but robustness of the Cauchy boundary has only recently been studied.
5.1 Computational boundaries
Boundary conditions are both the most important and the most difficult part of a theoretical treatment of most physical systems. Usually, that’s where all the physics is. And, in computational approaches, that’s usually where all the agony is. Computational boundaries for hyperbolic systems pose special difficulties. Even with an analytic form of the correct physical boundary condition in hand, there are seemingly infinitely more unstable numerical implementations than stable ones. In general, a stable problem places more boundary requirements on the finite difference equations than on the corresponding partial differential equations. Furthermore, the methods of linear stability analysis are often more unwieldy to apply to the boundary than to the interior evolution algorithm.
The von Neumann stability analysis of the interior algorithm linearizes the equations, while assuming a uniform grid with periodic boundary conditions, and checks that the discrete Fourier modes do not grow exponentially. There is an additional stability condition that a boundary introduces into this analysis. Consider the one-dimensional case. The mode ekx, with k real, is not included in the von Neumann analysis for periodic boundary conditions. However, for the half plane problem in the domain x ≤ 0, one can legitimately prescribe such a mode as initial data as long as k > 0 so that it has finite energy. Thus the stability of such boundary modes must be checked. In the case of an additional boundary, e.g. for a problem in the domain −1 ≤ x ≤ 1, the Godunov-Ryaben’kii theory gives as a necessary condition for stability the combined von Neumann stability of the interior and the stability of the allowed boundary modes [224]. The Kreiss condition [132] strengthens this result by providing a sufficient condition for stability.
The correct physical formulation of any Cauchy problem for an isolated system also involves asymptotic conditions at infinity. These conditions must ensure not only that the total energy and energy loss by radiation are both finite, but they must also ensure the proper 1/r asymptotic falloff of the radiation fields. However, when treating radiative systems computationally, an outer boundary is often established artificially at some large but finite distance in the wave zone, i.e. many wavelengths from the source. Imposing an appropriate radiation boundary condition at a finite distance is a difficult task even in the case of a simple radiative system evolving on a fixed geometric background. Gustaffson and Kreiss have shown in general that the construction of a nonreflecting boundary condition for an isolated system requires knowledge of the solution in a neighborhood of infinity [131].
When the system is nonlinear and not amenable to an exact solution, a finite outer boundary condition must necessarily introduce spurious physical effects into a Cauchy evolution. The domain of dependence of the initial Cauchy data in the region spanned by the computational grid would shrink in time along ingoing characteristics unless data on a worldtube traced out by the outer grid boundary is included as part of the problem. In order to maintain a causally sensible evolution, this worldtube data must correctly substitute for the missing Cauchy data which would have been supplied if the Cauchy hypersurface had extended to infinity. In a scattering problem, this missing exterior Cauchy data might, for instance, correspond to an incoming pulse initially outside the outer boundary. In a scalar wave problem with field Φ where the initial radiation is confined to a compact region inside the boundary, the missing Cauchy data outside the boundary would be Φ = Φ,t = 0 at the initial time t0. However, the determination of Cauchy data for general relativity is a global elliptic constraint problem so that there is no well defined scheme to confine it to a compact region. Furthermore, even in the scalar field case where Φ = Φ,t = 0 is appropriate Cauchy data outside the boundary at t0, it would still be a non-trivial evolution problem to correctly assign the associated boundary data for t ≥ t0.
It is common practice in computational physics to impose an artificial boundary condition (ABC), such as an outgoing radiation condition, in an attempt to approximate the proper data for the exterior region. This ABC may cause partial reflection of an outgoing wave back into the system [168, 154, 138, 202], which contaminates the accuracy of the interior evolution and the calculation of the radiated waveform. Furthermore, nonlinear waves intrinsically backscatter, which makes it incorrect to try to entirely eliminate incoming radiation from the outer region. The resulting error is of an analytic origin, essentially independent of computational discretization. In general, a systematic reduction of this error can only be achieved by moving the computational boundary to larger and larger radii. This is computationally very expensive, especially for 3-dimensional simulations.
A traditional ABC for the wave equation is the Sommerfeld condition. For a scalar field Φ satisfying the Minkowski space wave equation
with a smooth source S of compact support emitting outgoing radiation, the exterior retarded field has the form
where f, g and h and their derivatives are smooth bounded functions. The simplest case is the monopole radiation
which satisfies (∂t + ∂r)(rΦ) = 0. This motivates the use of the Sommerfeld condition
on a finite boundary r = R.
A homogeneous Sommerfeld condition, i.e. q = 0, is exact only in the spherically symmetric case. The Sommerfeld boundary data q in the general case (36) falls off as 1/R3, so that a homogeneous Sommerfeld condition introduces an error, which is small only for large R. As an example, for the dipole solution
we have
A homogeneous Sommerfeld condition at r = R would lead to a solution \({{\tilde \Phi}_{Dipole}}\) containing a reflected ingoing wave. For large R,
where ∂tf(t) = F(t) and the reflection coefficient has asymptotic behavior κ = O(1/R2). More precisely, the Fourier mode
satisfies the homogeneous boundary condition \(({\partial _t} + {\partial _r})(r{{\tilde \Phi}_{Dipole}}(\omega){\vert _R} = 0\) with reflection coefficient
Much work has been done on formulating boundary conditions, both exact and approximate, for linear problems in situations that are not spherically symmetric. These boundary conditions are given various names in the literature, e.g., absorbing or non-reflecting. A variety of ABCs have been reported for linear problems. See the articles [107, 202, 245, 209, 43] for general discussions.
Local ABCs have been extensively applied to linear problems with varying success [168, 89, 35, 244, 138, 52, 155]. Some of these conditions are local approximations to exact integral representations of the solution in the exterior of the computational domain [89], while others are based on approximating the dispersion relation of the so-called one-way wave equations [168, 244]. Higdon [138] showed that this last approach is essentially equivalent to specifying a finite number of angles of incidence for which the ABCs yield perfect transmission. Local ABCs have also been derived for the linear wave equation by considering the asymptotic behavior of outgoing solutions [35], thus generalizing the Sommerfeld outgoing radiation condition. Although this type of ABC is relatively simple to implement and has a low computational cost, the final accuracy is often limited because the assumptions made about the behavior of the waves are rarely met in practice [107, 245].
The disadvantages of local ABCs have led some workers to consider exact nonlocal boundary conditions based on integral representations of the infinite domain problem [243, 107, 245]. Even for problems where the Green’s function is known and easily computed, such approaches were initially dismissed as impractical [89]; however, the rapid increase in computer power has made it possible to implement exact nonlocal ABCs for the linear wave equation and Maxwell’s equations in 3D [80, 126]. If properly implemented, this method can yield numerical solutions to a linear problem which converge to the exact infinite domain problem in the continuum limit, while keeping the artificial boundary at a fixed distance. However, due to nonlocality, the computational cost per time step usually grows at a higher power with grid size \(({\mathcal O}({N^4})\) per time step in three dimensions) than in a local approach [107, 80, 245].
The extension of ABCs to nonlinear problems is much more difficult. The problem is normally treated by linearizing the region between the outer boundary and infinity, using either local or nonlocal linear ABCs [245, 209]. The neglect of the nonlinear terms in this region introduces an unavoidable error at the analytic level. But even larger errors are typically introduced in prescribing the outer boundary data. This is a subtle global problem because the correct boundary data must correspond to the continuity of fields and their normal derivatives when extended across the boundary into the linearized exterior. This is a clear requirement for any consistent boundary algorithm, since discontinuities in the field or its derivatives would otherwise act as a spurious sheet source on the boundary, which contaminates both the interior and the exterior evolutions. But the fields and their normal derivatives constitute an overdetermined set of data for the boundary problem. So it is necessary to solve a global linearized problem, not just an exterior one, in order to find the proper data. The designation “exact ABC” is given to an ABC for a nonlinear system whose only error is due to linearization of the exterior. An exact ABC requires the use of global techniques, such as the difference potentials method, to eliminate back reflection at the boundary [245].
There have been only a few applications of ABCs to strongly nonlinear problems [107]. Thompson [240] generalized a previous nonlinear ABC of Hedstrom [137] to treat 1D and 2D problems in gas dynamics. These boundary conditions performed poorly in some situations because of their difficulty in adequately modeling the field outside the computational domain [240, 107]. Hagstrom and Hariharan [133] have overcome these difficulties in 1D gas dynamics by a clever use of Riemann invariants. They proposed a heuristic generalization of their local ABC to 3D, but this approach has not yet been validated.
In order to reduce the level of approximation at the analytic level, an artificial boundary for a nonlinear problem must be placed sufficiently far from the strong-field region. This sharply increases the computational cost in multi-dimensional simulations [89]. There is no numerical method which converges (as the discretization is refined) to the infinite domain exact solution of a strongly nonlinear wave problem in multi-dimensions, while keeping the artificial boundary fixed. Attempts to use compactified Cauchy hypersurfaces which extend the domain to spatial infinity have failed because the phase of short wavelength radiation varies rapidly in spatial directions [154]. Characteristic evolution avoids this problem by approaching infinity along the phase fronts.
CCM is a strategy that eliminates this nonlinear source of error. In the simplest version of CCM, Cauchy and characteristic evolution algorithms are pasted together in the neighborhood of a worldtube to form a global evolution algorithm. The characteristic algorithm provides an outer boundary condition for the interior Cauchy evolution, while the Cauchy algorithm supplies an inner boundary condition for the characteristic evolution. The matching worldtube provides the geometric framework necessary to relate the two evolutions. The Cauchy foliation slices the worldtube into spherical cross-sections. The characteristic evolution is based upon the outgoing null hypersurfaces emanating from these slices, with the evolution proceeding from one hypersurface to the next by the outward radial march described in Section 3.1). There is no need to truncate spacetime at a finite distance from the source, since compactification of the radial null coordinate used in the characteristic evolution makes it possible to cover the infinite space with a finite computational grid. In this way, the true waveform may be computed up to discretization error by the finite difference algorithm.
5.2 The computational matching strategy
CCM evolves a mixed spacelike-null initial value problem in which Cauchy data is given in a spacelike hypersurface bounded by a spherical boundary \({\mathcal S}\) and characteristic data is given on a null hypersurface emanating from \({\mathcal S}\). The general idea is not entirely new. An early mathematical investigation combining spacelike and characteristic hypersurfaces appears in the work of Duff [88]. The three chief ingredients for computational implementation are: (i) a Cauchy evolution module, (ii) a characteristic evolution module and, (iii) a module for matching the Cauchy and characteristic regions across their interface. In the simplest scenario, the interface is the timelike worldtube which is traced out by the flow of \({\mathcal S}\) along the worldlines of the Cauchy evolution, as determined by the choice of lapse and shift. Matching provides the exchange of data across the worldtube to allow evolution without any further boundary conditions, as would be necessary in either a purely Cauchy or purely characteristic evolution. Other versions of CCM involve a finite overlap between the characteristic and Cauchy regions.
The most important application of CCM is anticipated to be the waveform and momentum recoil in the binary black hole inspiral and merger. The 3D Cauchy codes being applied to simulate this problem employ a single Cartesian coordinate patch. In principle, the application of CCM to this problem might seem routine, tantamount to translating into finite difference form the textbook construction of an atlas consisting of overlapping coordinate patches. In practice, it is a complicated project. The computational strategy has been outlined in [45]. The underlying algorithm consists of the following main submodules:
-
The boundary module which sets the grid structures. This defines masks identifying which points in the Cauchy grid are to be evolved by the Cauchy module and which points are to be interpolated from the characteristic grid, and vice versa. The reference structures for constructing the mask is the inner characteristic boundary, which in the Cartesian Cauchy coordinates is the “spherical” extraction worldtube \({x^2} + {y^2} + {z^2} = R_E^2\), and the outer Cauchy boundary \({x^2} + {y^2} + {z^2} = R_I^2\), where the Cauchy boundary data is injected. The choice of lapse and shift for the Cauchy evolution governs the dynamical and geometrical properties of these worldtubes.
-
The extraction module whose input is Cauchy grid data in the neighborhood of the extraction worldtube at RE and whose output is the inner boundary data for the exterior characteristic evolution. This module numerically implements the transformation from Cartesian {3 + 1} coordinates to spherical null coordinates. The algorithm makes no perturbative assumptions and is based upon interpolations of the Cauchy data to a set of prescribed grid points near RE. The metric information is then used to solve for the null geodesics normal to the slices of the extraction worldtube. This provides the Jacobian for the transformation to null coordinates in the neighborhood of the worldtube. The characteristic evolution module is then used to propagate the data from the worldtube to null infinity, where the waveform is calculated.
-
The injection module which completes the interface by using the exterior characteristic evolution to inject the outer boundary data for the Cauchy evolution at RI. This is the inverse of the extraction procedure but must be implemented with RI > RE to allow for overlap between the Cauchy and characteristic domains. The overlap region can be constructed either to have a fixed physical size or to shrink to zero in the continuum limit. In the latter case, the inverse Jacobian describing the transformation from null to Cauchy coordinates can be obtained to prescribed accuracy in terms of an affine parameter expansion along the null geodesics emanating from the worldtube. The numerical stability of this element of the scheme is not guaranteed.
The above strategy provides a model of how Cauchy and characteristic codes can be pieced together as modules to form a global evolution code.
The full advantage of CCM lies in the numerical treatment of nonlinear systems where its error converges to zero in the continuum limit of infinite grid resolution [38, 39, 76]. For high accuracy, CCM is also the most efficient method. For small target error ε, it has been shown that the relative amount of computation required for CCM (ACCM) compared to that required for a pure Cauchy calculation (AC) goes to zero, ACCM/AC → O as ε → O [49, 45]. An important factor here is the use of a compactified characteristic evolution, so that the whole spacetime is represented on a finite grid. From a numerical point of view this means that the only error made in a calculation of the radiation waveform at infinity is the controlled error due to the finite discretization. Accuracy of a Cauchy algorithm which uses an ABC requires a large grid domain in order to avoid error from nonlinear effects in its exterior. The computational demands of CCM are small because the interface problem involves one less dimension than the evolution problem. Because characteristic evolution algorithms are more efficient than Cauchy algorithms, the efficiency can be further enhanced by making the matching radius as small as possible consistent with the avoidance of caustics.
At present, the computational strategy of CCM is mainly the tool of numerical relativists, who are used to dealing with dynamical coordinate systems. The first discussion of its potential was given in [38] and its feasibility has been more fully explored in [76, 77, 87, 42, 236]. Recent work has been stimulated by the requirements of the binary black hole problem, where CCM is one of the strategies to provide boundary conditions and determine the radiation waveform. However, it also has inherent advantages in dealing with other hyperbolic systems in computational physics, particularly nonlinear 3-dimensional problems. A detailed study of the stability and accuracy of CCM for linear and nonlinear wave equations has been presented in [43], illustrating its potential for a wide range of problems.
5.3 The outer Cauchy boundary in numerical relativity
A special issue arising in general relativity is whether the boundary conditions on an outer world-tube preserve the constraints. It is typical of hyperbolic reductions of the Einstein equations that the Hamiltonian and momentum constraints propagate in a domain of dependence dictated by the characteristics. Unless the boundary conditions enforce these constraints, they will be violated outside the domain of dependence of the initial Cauchy hypersurface. This issue of a constraint-preserving initial boundary value problem has only recently been addressed [232]. The first fully nonlinear treatment of a well-posed constraint preserving formulation of the Einstein initial-boundary value problem (IBVP) has subsequently been given by Friedrich and Nagy [98]. Their treatment is based upon a frame formulation in which the evolution variables are the tetrad, connection coefficients and Weyl curvature. Although this system has not yet been implemented computationally, it has spurred the investigation of simpler treatments of Einstein equations which give rise to a constraint preserving IBVP under various restrictions [63, 236, 64, 100, 128, 207, 162]. See [213] for a review.
Well-posedness of the IBVP, in addition to constraint preservation, is a necessary condition for computational success. This is particularly cogent for dealing with waveform extraction in the simulation of black holes by BSSN or harmonic formulations. There is no well-posed outer boundary theory for the BSSN formulation and the strategy is to place the boundary out far enough so that it does no harm. The harmonic formulation has a simpler mathematical structure as a system of coupled quasilinear wave equations which is more amenable to an analytic treatment.
Standard harmonic coordinates satisfy the covariant wave equation
(This can easily be generalized to include gauge forcing [97], whereby Γα = fα(xβ, gβγ). For simplicity of discussion, I will set Γα = 0, although gauge forcing is an essential tool in simulating black holes [195].)
When Γα = 0, Einstein’s equations reduce to the 10 quasilinear wave equations
where Sαβ does not enter the principle part and vanishes in the linearized approximation. Straightforward techniques can be applied to formulate a well-posed IBVP for the system (45). The catch is that Einstein’s equations are not necessarily satisfied unless the constraints are also satisfied.
In the harmonic formalism, the constraints can be reduced to the harmonic coordinate conditions (44). For the resulting IBVP to be constraint preserving, these harmonic conditions must be built into the boundary condition. Numerous early attempts to accomplish this failed because (44) contains derivatives tangent to the boundary, which do not fit into the standard methods for obtaining the necessary energy estimates. The use of pseudo-differential techniques developed for similar problems in elasticity theory has led to the first well-posed formulation for the general IBVP for the harmonic Einstein equations [162]. Subsequently, these results were also obtained using standard energy estimates by means of a novel, non-conventional choice of the energy for the harmonic system [160]. Furthermore, the allowed boundary conditions include those of the Sommerfeld type which are nonreflecting in the sense that the boundary data for gμν falls off as O(1/R4) as the boundary radius R → ∞ of [161]
A Cauchy evolution code, the Abigel code, has been based upon a discretized of this well-posed harmonic IBVP [236]. The code was tested to be stable, convergent and constraint preserving in the nonlinear regime [16]. A linearized version of the Abigel code has been used to successfully carry out CCM (see Section 5.8).
In the present harmonic codes used to simulate the binary black holes, the best that can be done is to impose a constraint preserving boundary condition for which homogeneous boundary data, i.e. zero boundary values, is a good approximation. One proposal of this type [98] is a boundary condition that requires the Newman-Penrose [179] Weyl tensor component Ψ0 to vanish. In the limit that the outer boundary goes to infinity this outer boundary condition becomes exact. In the present state of the art of black hole simulations, this approach comes closest to a satisfactory treatment of the outer boundary [205].
5.4 Perturbative matching schemes
In numerous analytic studies outside of general relativity, matching techniques have successfully cured pathologies in perturbative expansions [178]. Matching is a strategy for obtaining a global solution by patching together solutions obtained using different coordinate systems for different regions. By adopting each coordinate system to a length scale appropriate to its domain, a globally convergent perturbation expansion is sometimes possible in cases where a single coordinate system would fail.
In general relativity, Burke showed that matching could be used to eliminate some of the divergences arising in perturbative calculations of gravitational radiation [59]. Kates and Kegles further showed that use of an exterior null coordinate system in the matching scheme could eliminate problems in the perturbative treatment of a scalar radiation field on a Schwarzschild background [156]. The Schwarzschild light cones have drastically different asymptotic behavior from the artificial Minkowski light cones used in perturbative expansions based upon a flat space Green function. Use of the Minkowski light cones leads to nonuniformities in the expansion of the radiation fields which are eliminated by the use of true null coordinates in the exterior. Kates, Anderson, Kegles, and Madonna extended this work to the fully general relativistic case and reached the same conclusion [10]. Anderson later applied this approach to the slow motion approximation of a binary system and obtained a derivation of the radiation reaction effect on the orbital period which avoided some objections to earlier approaches [6]. The use of the true light cones was also essential in formulating as a mathematical theorem that the Bondi news function satisfies the Einstein quadrupole formula to leading order in a Newtonian limit [250]. Although questions of mathematical consistency still remain in the perturbative treatment of gravitational radiation, it is clear that the use of characteristic methods pushes these problems to a higher perturbative order.
One of the first computational applications of characteristic matching was a hybrid numerical-analytical treatment by Anderson and Hobill of the test problem of nonlinear 1D scalar waves [7, 8, 9]. They matched an inner numerical solution to a far field solution which was obtained by a perturbation expansion. A key ingredient is that the far field is solved in retarded null coordinates (u,r). Because the transformation from null coordinates (u,r) to Cauchy coordinates (t,r) is known analytically for this problem, the matching between the null and Cauchy solutions is quite simple. Causality was enforced by requiring that the system be stationary prior to some fixed time. This eliminates extraneous incoming radiation in a physically correct way in a system which is stationary prior to a fixed time but it is nontrivial to generalize, say, to the problem of radiation from an orbiting binary.
Later, a global, characteristic, numerical study of the self-gravitating version of this problem confirmed that the use of the true null cones is essential in getting the correct radiated waveform [123]. For quasi-periodic radiation, the phase of the waveform is particular sensitive to the truncation of the outer region at a finite boundary. Although a perturbative estimate would indicate an \({\mathcal O}(M/R)\) error, this error accumulates over many cycles to produce an error of order π in the phase.
Anderson and Hobill proposed that their method be extended to general relativity by matching a numerical solution to an analytic 1/r expansion in null coordinates. Most perturbative-numerical matching schemes that have been implemented in general relativity have been based upon perturbations of a Schwarzschild background using the standard Schwarzschild time slicing [1, 4, 2, 3, 208, 204, 177]. It would be interesting to compare results with an analytic-numeric matching scheme based upon the true null cones. Although the full proposal by Anderson and Hobill has not been carried out, characteristic techniques have been used [170, 65, 151] to study the radiation content of numerical solutions by treating the far field as a perturbation of a Schwarzschild spacetime.
Most metric based treatments of gravitational radiation are based upon perturbations of the Schwarzschild metric and solve the underlying Regge-Wheeler [200] and Zerilli [254] equations using traditional spacelike Cauchy hypersurfaces. At one level, these approaches extract the radiation from a numerical solution in a region with outer boundary \({\mathcal B}\) by using data on an inner worldtube \({\mathcal W}\) to construct the perturbative solution. Ambiguities are avoided by use of Moncrief’s gauge invariant perturbation quantities [175]. For this to work, \({\mathcal W}\) must not only be located in the far field, i.e. many wavelengths from the source, but, because of the lack of proper outer boundary data, it is necessary that the boundary \({\mathcal B}\) be sufficiently far outside \({\mathcal W}\) so that the extracted radiation is not contaminated by back-reflection for some significant window of time. This poses extreme computational requirements in a 3D problem. This extraction strategy has also been carried out using characteristic evolution in the exterior of \({\mathcal W}\) instead of a perturbative solution, i.e. Cauchy-characteristic extraction [49] (see Section 6).
A study by Babiuc, Szilágyi, Hawke, and Zlochower carried out in the perturbative regime [13] show that CCE compares favorably with Zerilli extraction and has advantages at small extraction radii. When the extraction worldtube is sufficiently large, e.g. r = 200λ, where λ is the characteristic wavelength of the radiation, the Zerilli and CCE methods both give excellent results. However, the accuracy of CCE remains unchanged at small extraction radii, e.g. r = 10λ, whereas the Zerilli approach shows error associated with near zone effects.
The contamination of the extracted radiation by back-reflection can only be eliminated by matching to an exterior solution which injects the physically appropriate boundary data on \({\mathcal W}\). Cauchy-perturbative matching [208, 204] has been implemented using the same modular structure described for CCM in Section 5.2. Nagar and Rezzolla [177] have given a review of this approach. At present, perturbative matching and CCM share the common problem of long term stability of the outer Cauchy boundary in 3D applications.
5.5 Cauchy-characteristic matching for 1D gravitational systems
The first numerical implementations of CCM were 1D feasibility studies. These model problems provided a controlled environment for the development of CCM, in which either exact solutions or independent numerical solutions were known. In the following studies CCM worked like a charm in a variety of 1D applications, i.e. the matched evolutions were essentially transparent to the presence of the interface.
5.5.1 Cylindrical matching
The Southampton group chose cylindrically symmetric systems as their model problem for developing matching techniques. In preliminary work, they showed how CCM could be consistently carried out for a scalar wave evolving in Minkowski spacetime but expressed in a nontrivial cylindrical coordinate system [76].
They then tackled the gravitational problem. First they set up the analytic machinery necessary for investigating cylindrically symmetric vacuum spacetimes [77]. Although the problem involves only one spatial dimension, there are two independent modes of polarization. The Cauchy metric was treated in the Jordan-Ehlers-Kompaneets canonical form, using coordinates (t, r, ϕ, z) adapted to the (ϕ, z) cylindrical symmetry. The advantage here is that u = t − r is then a null coordinate which can be used for the characteristic evolution. They successfully recast the equations in a suitably regularized form for the compactification of \({{\mathcal I}^ +}\) in terms of the coordinate \(y = \sqrt {1/r}\). The simple analytic relationship between Cauchy coordinates (t, r) and characteristic coordinates (u, y) facilitated the translation between Cauchy and characteristic variables on the matching worldtube, given by r = const.
Next they implemented the scheme as a numerical code. The interior Cauchy evolution was carried out using an unconstrained leapfrog scheme. It is notable that they report no problems with instability, which have arisen in other attempts at unconstrained leapfrog evolution in general relativity. The characteristic evolution also used a leapfrog scheme for the evolution between retarded time levels u, while numerically integrating the hypersurface equations outward along the characteristics.
The matching interface was located at points common to both the Cauchy and characteristic grids. In order to update these points by Cauchy evolution, it was necessary to obtain field values at the Cauchy “ghost” points which lie outside the worldtube in the characteristic region. These values were obtained by interpolation from characteristic grid points (lying on three levels of null hypersurfaces in order to ensure second order accuracy). Similarly, the boundary data for starting up the characteristic integration was obtained by interpolation from Cauchy grid values inside the worldtube.
The matching code was first tested [87] using exact Weber-Wheeler cylindrical waves [247], which come in from \({{\mathcal I}^ -}\), pass through the symmetry axis and expand out to \({{\mathcal I}^ +}\). The numerical errors were oscillatory with low growth rate, and second order convergence was confirmed. Of special importance, little numerical noise was introduced by the interface. Comparisons of CCM were made with Cauchy evolutions using a standard outgoing radiation boundary condition [190]. At high amplitudes the standard condition developed a large error very quickly and was competitive only for weak waves with a large outer boundary. In contrast, the matching code performed well even with a small matching radius. Some interesting simulations were presented in which an outgoing wave in one polarization mode collided with an incoming wave in the other mode, a problem studied earlier by pure Cauchy evolution [192]. The simulations of the collision were qualitatively similar in these two studies.
The Weber-Wheeler waves contain only one gravitational degree of freedom. The code was next tested [84] using exact cylindrically symmetric solutions, due to Piran, Safier, and Katz [191], which contain both degrees of freedom. These solutions are singular at \({{\mathcal I}^ +}\) so that the code had to be suitably modified. Relative errors of the various metric quantities were in the range 10−4 to 10−2. The convergence rate of the numerical solution starts off as second order but diminishes to first order after long time evolution. This performance could perhaps be improved by incorporating subsequent improvements in the characteristic code made by Sperhake, Sjödin, and Vickers (see Section 3.1).
5.5.2 Spherical matching
A joint collaboration between groups at Pennsylvania State University and the University of Pittsburgh applied CCM to the EKG system with spherical symmetry [115]. This model problem allowed simulation of black hole formation as well as wave propagation.
The geometrical setup is analogous to the cylindrically symmetric problem. Initial data were specified on the union of a spacelike hypersurface and a null hypersurface. The evolution used a 3-level Cauchy scheme in the interior and a 2-level characteristic evolution in the compactified exterior. A constrained Cauchy evolution was adopted because of its earlier success in accurately simulating scalar wave collapse [68]. Characteristic evolution was based upon the null parallelogram algorithm (8). The matching between the Cauchy and characteristic foliations was achieved by imposing continuity conditions on the metric, extrinsic curvature and scalar field variables, ensuring smoothness of fields and their derivatives across the matching interface. The extensive analytical and numerical studies of this system in recent years aided the development of CCM in this non-trivial geometrical setting by providing basic knowledge of the expected physical and geometrical behavior, in the absence of exact solutions.
The CCM code accurately handled wave propagation and black hole formation for all values of M/R at the matching radius, with no symptoms of instability or back-reflection. Second order accuracy was established by checking energy conservation.
5.5.3 Excising 1D black holes
In further developmental work on the EKG model, the Pittsburgh group used CCM to formulate a new treatment of the inner Cauchy boundary for a black hole spacetime [119]. In the excision strategy, the inner boundary of the Cauchy evolution is located at an apparent horizon, which must lie inside (or on) the event horizon [246], so that truncation of the interior spacetime at the apparent horizon cannot causally affect the gravitational waves radiated to infinity. This is the physical rationale behind the apparent horizon boundary condition. However, instabilities reported in some early attempts at excision motivated an alternative treatment.
In the CCM excision strategy, illustrated in Figure 6, the interior black hole region is evolved using an ingoing null algorithm whose inner boundary is a marginally trapped surface, and whose outer boundary lies outside the black hole and forms the inner boundary of a region evolved by the Cauchy algorithm. In turn, the outer boundary of the Cauchy region is handled by matching to an outgoing null evolution extending to \({{\mathcal I}^ +}\). Data are passed between the inner characteristic and central Cauchy regions using a CCM procedure similar to that already described for an outer Cauchy boundary. The main difference is that, whereas the outer Cauchy boundary data is induced from the Bondi metric on an outgoing null hypersurface, the inner Cauchy boundary is now obtained from an ingoing null hypersurface which enters the event horizon and terminates at a marginally trapped surface.
Black hole excision by matching. A Cauchy evolution, with data at t0 is matched across worldtubes R0 and R1 to an ingoing null evolution, with data at υ0, and an outgoing null evolution, with data at u0. The ingoing null evolution extends to an inner trapped boundary Q, and the outgoing null evolution extends to \({{\mathcal I}^ +}\).
The translation from an outgoing to an incoming null evolution algorithm can be easily carried out. The substitution β → β + iπ/2 in the 3D version of the Bondi metric (3) provides a simple formal recipe for switching from an outgoing to an ingoing null formalism [119].
In order to ensure that trapped surfaces exist on the ingoing null hypersurfaces, initial data were chosen which guarantee black hole formation. Such data can be obtained from initial Cauchy data for a black hole. However, rather than extending the Cauchy hypersurface inward to an apparent horizon, it was truncated sufficiently far outside the apparent horizon to avoid computational problems with the Cauchy evolution. The initial Cauchy data were then extended into the black hole interior as initial null data until a marginally trapped surface was reached. Two ingredients were essential in order to arrange this. First, the inner matching surface must be chosen to be convex, in the sense that its outward null normals uniformly diverge and its inner null normals uniformly converge. (This is trivial to satisfy in the spherically symmetric case.) Given any physically reasonable matter source, the focusing theorem guarantees that the null rays emanating inward from the matching sphere continue to converge until reaching a caustic. Second, the initial null data must lead to a trapped surface before such a caustic is encountered. This is a relatively easy requirement to satisfy because the initial null data can be posed freely, without any elliptic or algebraic constraints other than continuity with the Cauchy data.
A code was developed which implemented CCM at both the inner and outer boundaries [119]. Its performance showed that CCM provides as good a solution to the black hole excision problem in spherical symmetry as any previous treatment [214, 215, 171, 11]. CCM is computationally more efficient than these pure Cauchy approaches (fewer variables) and much easier to implement. Depending upon the Cauchy formalism adopted, achieving stability with a pure Cauchy scheme in the region of an apparent horizon can be quite tricky, involving much trial and error in choosing finite difference schemes. There were no complications with stability of the null evolution at the marginally trapped surface.
The Cauchy evolution was carried out in ingoing Eddington-Finklestein (IEF) coordinates. The initial Cauchy data consisted of a Schwarzschild black hole with an ingoing Gaussian pulse of scalar radiation. Since IEF coordinates are based on ingoing null cones, it is possible to construct a simple transformation between the IEF Cauchy metric and the ingoing null metric. Initially there was no scalar field present on either the ingoing or outgoing null patches. The initial values for the Bondi variables β and V were determined by matching to the Cauchy data at the matching surfaces and integrating the hypersurface equations (5, 6).
As the evolution proceeds, the scalar field passes into the black hole, and the marginally trapped surface (MTS) grows outward. The MTS is easily located in the spherically symmetric case by an algebraic equation. In order to excise the singular region, the grid points inside the marginally trapped surface were identified and masked out of the evolution. The backscattered radiation propagated cleanly across the outer matching surface to \({{\mathcal I}^ +}\). The strategy worked smoothly, and second order accuracy of the approach was established by comparing it to an independent numerical solution obtained using a second order accurate, purely Cauchy code [171]. As discussed in Section 5.9, this inside-outside application of CCM has potential application to the binary black hole problem.
In a variant of this double CCM matching scheme, Lehner [164] has eliminated the middle Cauchy region between R0 and R1 in Figure 6. He constructed a 1D code matching the ingoing and outgoing characteristic evolutions directly across a single timelike worldtube. In this way, he was able to simulate the global problem of a scalar wave falling into a black hole by purely characteristic methods.
5.6 Axisymmetric Cauchy-characteristic matching
The Southampton CCM project is being carried out for spacetimes with (twisting) axial symmetry. The formal basis for the matching scheme was developed by d’Inverno and Vickers [85, 86]. Similar to the Pittsburgh 3D strategy (see Section 5.2), matching is based upon an extraction module, which supplies boundary data for the exterior characteristic evolution, and an injection module, which supplies boundary data for the interior Cauchy evolution. However, their use of spherical coordinates for the Cauchy evolution (as opposed to Cartesian coordinates in the 3D strategy) allows use of a matching worldtube r = Rm which lies simultaneously on Cauchy and characteristic gridpoints. This tremendously simplifies the necessary interpolations between the Cauchy and characteristic evolutions, at the expense of dealing with the r = 0 coordinate singularity in the Cauchy evolution. The characteristic code (see Section 3.3.4) is based upon a compactified Bondi-Sachs formalism. The use of a “radial” Cauchy gauge, in which the Cauchy coordinate r measures the surface area of spheres, simplifies the relation to the Bondi-Sachs coordinates. In the numerical scheme, the metric and its derivatives are passed between the Cauchy and characteristic evolutions exactly at r = Rm, thus eliminating the need of a matching interface encompassing a few grid zones, as in the 3D Pittsburgh scheme. This avoids a great deal of interpolation error and computational complexity.
Preliminary results in the development of the Southampton CCM code are described by Pollney in his thesis [194]. The Cauchy code was based upon the axisymmetric ADM code of Stark and Piran [228] and reproduces their vacuum results for a short time period, after which an instability at the origin becomes manifest. The characteristic code has been tested to reproduce accurately the Schwarzschild and boost-rotation symmetric solutions [37], with more thorough tests of stability and accuracy still to be carried out.
5.7 Cauchy-characteristic matching for 3D scalar waves
CCM has been successfully implemented in the fully 3D problem of nonlinear scalar waves evolving in a flat spacetime [43, 42]. This study demonstrated the feasibility of matching between Cartesian Cauchy coordinates and spherical null coordinates, the setup required to apply CCM to the binary black hole problem. Unlike spherically or cylindrically symmetric examples of matching, the Cauchy and characteristic patches do not share a common coordinate which can be used to define the matching interface. This introduces a major complication into the matching procedure, resulting in extensive use of intergrid interpolation. The accompanying short wavelength numerical noise presents a challenge in obtaining a stable algorithm.
The nonlinear waves were modeled by the equation
with self-coupling F(Φ) and external source S. The initial Cauchy data Φ(t0, x, y, z) and ∂tΦ(t0, x, y, z) are assigned in a spatial region bounded by a spherical matching surface of radius Rm.
The characteristic initial value problem (46) is expressed in standard spherical coordinates (r, θ, φ) and retarded time u = t − r + Rm:
where g = rΦ and L2 is the angular momentum operator
The initial null data consist of g(r, θ, φ, u0) on the outgoing characteristic cone u0 = t0 emanating at the initial Cauchy time from the matching worldtube at r = Rm.
CCM was implemented so that, in the continuum limit, Φ and its normal derivatives would be continuous across the matching interface. The use of a Cartesian discretization in the interior and a spherical discretization in the exterior complicated the treatment of the interface. In particular, the stability of the matching algorithm required careful attention to the details of the intergrid matching. Nevertheless, there was a reasonably broad range of discretization parameters for which CCM was stable.
Two different ways of handling the spherical coordinates were used. One was based upon two overlapping stereographic grid patches and the other upon a multiquadric approximation using a quasi-regular triangulation of the sphere. Both methods gave similar accuracy. The multiquadric method showed a slightly larger range of stability. Also, two separate tactics were used to implement matching, one based upon straightforward interpolations and the other upon maintaining continuity of derivatives in the outward null direction (a generalization of the Sommerfeld condition). Both methods were stable for a reasonable range of grid parameters. The solutions were second order accurate and the Richardson extrapolation technique could be used to accelerate convergence.
The performance of CCM was compared to traditional ABCs. As expected, the nonlocal ABCs yielded convergent results only in linear problems, and convergence was not observed for local ABCs, whose restrictive assumptions were violated in all of the numerical experiments. The computational cost of CCM was much lower than that of current nonlocal boundary conditions. In strongly nonlinear problems, CCM appears to be the only available method which is able to produce numerical solutions which converge to the exact solution with a fixed boundary.
5.8 Stable 3D linearized Cauchy-characteristic matching
Although the individual pieces of the CCM module have been calibrated to give a second order accurate interface between Cauchy and characteristic evolution modules in 3D general relativity, its stability has not yet been established [45]. However, a stable version of CCM for linearized gravitational theory has recently been demonstrated [236]. The Cauchy evolution is carried out using a harmonic formulation for which the reduced equations have a well-posed initial-boundary problem. Previous attempts at CCM were plagued by boundary induced instabilities of the Cauchy code. Although stable behavior of the Cauchy boundary is only a necessary and not a sufficient condition for CCM, the tests with the linearized harmonic code matched to a linearized characteristic code were successful.
The harmonic conditions consist of wave equations for the coordinates which can be used to propagate the gauge as four scalar waves using characteristic evolution. This allows the extraction worldtube to be placed at a finite distance from the injection worldtube without introducing a gauge ambiguity. Furthermore, the harmonic gauge conditions are the only constraints on the Cauchy formalism so that gauge propagation also insures constraint propagation. This allows the Cauchy data to be supplied in numerically benign Sommerfeld form, without introducing constraint violation. Using random initial data, robust stability of the CCM algorithm was confirmed for 2000 crossing times on a 453 Cauchy grid. Figure 7 shows a sequence of profiles of the metric component \({\gamma ^{xy}} = \sqrt {- g} {g^{xy}}\) linearized wave propagates cleanly through the spherical injection boundary and passes to the characteristic grid, where it is propagated to \({{\mathcal I}^ +}\).
5.9 The binary black hole inner boundary
CCM also offers a new approach to singularity excision in the binary black hole problem in the manner described in Section 5.5.3 for a single spherically symmetric black hole. In a binary system, there are computational advantages in posing the Cauchy evolution in a frame which is co-rotating with the orbiting black holes. In this co-orbiting description, the Cauchy evolution requires an inner boundary condition inside the black holes and also an outer boundary condition on a worldtube outside of which the grid rotation is likely to be superluminal. An outgoing characteristic code can routinely handle such superluminal gauge flows in the exterior [46]. Thus, successful implementation of CCM could solve the exterior boundary problem for this co-orbiting description.
CCM also has the potential to handle the two black holes inside the Cauchy region. As described earlier with respect to Figure 6, an ingoing characteristic code can evolve a moving black hole with long term stability [119, 116]. This means that CCM might also be able to provide the inner boundary condition for Cauchy evolution once stable matching has been accomplished. In this approach, the interior boundary of the Cauchy evolution is located outside the apparent horizon and matched to a characteristic evolution based upon ingoing null cones. The inner boundary for the characteristic evolution is a trapped or marginally trapped surface, whose interior is excised from the evolution.
In addition to restricting the Cauchy evolution to the region outside the black holes, this strategy offers several other advantages. Although finding a marginally trapped surface on the ingoing null hypersurfaces remains an elliptic problem, there is a natural radial coordinate system (r, θ, ϕ) to facilitate its solution. Motion of the black hole through the grid reduces to a one-dimensional radial problem, leaving the angular grid intact and thus reducing the computational complexity of excising the inner singular region. (The angular coordinates can even rotate relative to the Cauchy coordinates in order to accommodate spinning black holes.) The chief danger in this approach is that a caustic might be encountered on the ingoing null hypersurface before entering the trapped region. This is a gauge problem whose solution lies in choosing the right location and geometry of the surface across which the Cauchy and characteristic evolutions are matched. There is a great deal of flexibility here because the characteristic initial data can be posed without constraints.
This global strategy is tailor-made to treat two black holes in the co-orbiting gauge, as illustrated in Figure 8. Two disjoint characteristic evolutions based upon ingoing null cones are matched across worldtubes to a central Cauchy region. The interior boundaries of each of these interior characteristic regions border a trapped surface. At the outer boundary of the Cauchy region, a matched characteristic evolution based upon outgoing null hypersurfaces propagates the radiation to infinity.
CCM for binary black holes, portrayed in a co-rotating frame. The Cauchy evolution is matched across two inner worldtubes Γ1 and Γ2 to two ingoing null evolutions whose inner boundaries excise the individual black holes. The outer Cauchy boundary is matched across the worldtube Γ to an outgoing null evolution extending to \({{\mathcal I}^ +}\).
Present characteristic and Cauchy codes can handle the individual pieces of this problem. Their unification offers a new approach to simulating the inspiral and merger of two black holes. The individual pieces of the fully nonlinear CCM module, as outlined in Section 5.2, have been implemented and tested for accuracy. The missing ingredient is long term stability in the nonlinear gravitational case, which would open the way to future applications.
6 Cauchy-Characteristic Extraction of Waveforms
When an artificial finite outer boundary is introduced there are two broad sources of error:
-
The outer boundary condition
-
Waveform extraction at an inner worldtube.
CCM addresses both of these items. Cauchy-characteristic extraction (CCE), which is one of the pieces of the CCM strategy, offers a means to avoid the second source of error introduced by extraction at a finite worldtube. In current codes used to simulate black holes, the waveform is extracted at an interior worldtube which must be sufficiently far inside the outer boundary in order to isolate it from errors introduced by the boundary condition. There the waveform is extracted by a perturbative scheme based upon the introduction of a background Schwarzschild spacetime. This has been carried out using the Regge-Wheeler-Zerilli [200, 254] treatment of the perturbed metric, as reviewed in [177], and also by calculating the Newman-Penrose Weyl component Ψ4, as first done for the binary black hole problem in [17, 195, 66, 18]. In this approach, errors arise from the finite size of the extraction worldtube, from nonlinearities and from gauge ambiguities involved in the arbitrary introduction of a background metric. The gauge ambiguities might seem less severe in the case of Ψ4 (vs metric) extraction, but there are still delicate problems associated with the choices of a preferred null tetrad and preferred worldlines along which to measure the waveform (see [167] for an analysis).
CCE offers a means to avoid this error introduced by extraction at a finite worldtube. In CCE, the inner worldtube data supplied by the Cauchy evolution is used as boundary data for a characteristic evolution to future null infinity, where the waveform can be unambiguously computed in terms of the Bondi news function. By itself, CCE does not use the characteristic evolution to inject outer boundary data for the Cauchy evolution, which can be a source of instability in full CCM. A wide number of highly nonlinear tests involving black holes [46, 255, 256] have shown that CCE is a stable procedure which provides the gravitational waveform up to numerical error which is second order convergent. Nevertheless, in astrophysical applications which require high resolution, such as the inspiral of matter into a black hole [44], numerical error has been a troublesome factor in computing the news function. The CCE modules were developed in a past period when stability was the dominant issue and second order accuracy was considered sufficient. Only recently have they begun to be updated to include the more accurate techniques now standard in Cauchy codes. There are two distinct ways, geometric and numerical, that the accuracy of CCE might be improved. In the geometrical category, one option is to compute Ψ4 instead of the news function as the primary description of the waveform. In the numerical category, some standard methods for improving accuracy, such as higher order finite difference approximations, are straightforward to implement whereas others, such as adaptive mesh refinement, have only been tackled for 1D characteristic codes [197].
A major source of numerical error in characteristic evolution arises from the intergrid interpolations arising from the multiple patches necessary to coordinatize the spherical cross-sections of the outgoing null hypersurfaces. More accurate methods have been developed to reduce this interpolation error, as discussed in Section 4.1. In a test problem involving a scalar wave Φ, the accuracies of the circular-stereographic and cubed-sphere methods were compared [14]. For equivalent computational expense, the cubed-sphere error in the scalar field \({\mathcal E}(\Phi)\) was \(\approx {1 \over 3}\) the circular-stereographic error but the advantage was smaller for the higher ð-derivatives (angular derivatives) required in gravitational waveform extraction. The cubed-sphere error \({\mathcal E}({\bar \eth\eth^2}\Phi)\) was \(\approx {4 \over 5}\) the stereographic error.
In order to appreciate why waveforms are not easy to extract accurately it is worthwhile to review the calculation of the required asymptotic quantities. A simple approach to Penrose compactification is by introducing an inverse surface area coordinate ℓ = 1/r, so that future null infinity \({{\mathcal I}^ +}\) is given by ℓ = 0 [237]. In the resulting xμ = (u, ℓ, xA) Bondi coordinates, where u is the retarded time defined on the outgoing null hypersurfaces and xA are angular coordinates along the outgoing null rays, the physical space-time metric gμν has conformal compactification \({{\hat g}_{\mu \nu}} = {\ell ^2}{g_{\mu \nu}}\) of the form
where α, β, UA and hAB are smooth fields at \({{\mathcal I}^ +}\).
The news function and Weyl component Ψ4, which describe the radiation, are constructed from the leading coefficients in an expansion of \({{\hat g}_{\mu \nu}}\) in powers of ℓ. The requirement of asymptotic flatness imposes relations between these expansion coefficients. In terms of the Einstein tensor \({{\hat G}_{\mu \nu}}\) and covariant derivative \({{\hat \nabla}_\mu}\) associated with \({{\hat g}_{\mu \nu}}\), the vacuum Einstein equations become
Asymptotic flatness immediately implies that \({{\hat g}^{\ell \ell}} = ({{\hat \nabla}^\alpha}\ell){{\hat \nabla}_\alpha}\ell = O(\ell)\) so that \({{\mathcal I}^ +}\) is a null hypersurface with generators in the \({{\hat \nabla}^\mu}\ell\) direction. From (50) there also follows the existence of a smooth trace-free field \({{\hat \Sigma}_{\mu \nu}}\) defined on \({{\mathcal I}^ +}\) by
where \(\hat \Theta: = {{\hat \nabla}^\mu}{{\hat \nabla}_\mu}\ell\) is the expansion of \({{\mathcal I}^ +}\). The expansion \({\hat \Theta}\) depends upon the conformal factor used to compactify \({{\mathcal I}^ +}\). In an inertial conformal Bondi frame, tailored to a standard Minkowski metric at \({{\mathcal I}^ +},\hat \Theta = 0\). But this is not the case for the computational frame used in characteristic evolution, which is determined by conditions on the inner extraction worldtube.
The gravitational waveform depends on \({{\hat \Sigma}_{\mu \nu}}\), which in turn depends on the leading terms in the expansion of \({{\hat g}_{\mu \nu}}\):
In an inertial conformal Bondi frame, HAB = QAB (the unit sphere metric), H = LA = 0 and the Bondi news function reduces to the simple form
where QA is a complex polarization dyad on the unit sphere, i.e. \({Q^{AB}} = {Q^{(A}}{{\bar Q}^{B)}}\) The spin rotation freedom Qβ → e−iγQβ is fixed by parallel propagation along the generators of \({{\mathcal I}^ +}\), so that the real and imaginary parts of N correctly describe the ⊕ and ⊗ polarization modes of inertial observers at \({{\mathcal I}^ +}\).
However, in the computational frame the news function has the more complicated form
where ω is the conformal factor relating HAB to the unit sphere metric, i.e. QAB = ω2HAB. The conformal factor obeys the elliptic equation governing the conformal transformation relating the metric of the cross-sections of \({{\mathcal I}^ +}\) to the unit sphere metric,
where \({\mathcal R}\) is the curvature scalar and DA the covariant derivative associated with HAB. By first solving (55) at the initial retarded time, ω can then be determined at later times by evolving it according to the asymptotic relation
All of these procedures introduce numerical error which presents a a challenge for computational accuracy, especially because of the appearance of second angular derivatives of ω in the news function (54).
Similar complications appear in Ψ4 extraction. Asymptotic flatness implies that the Weyl tensor vanishes at \({{\mathcal I}^ +}\), i.e. Ĉμνρσ = O(ℓ). This is the conformal space statement of the peeling property [187]. Let \(({{\hat n}^\mu},{{\hat \ell}^\mu},{{\hat m}^\mu})\) be an orthonormal null tetrad such that \({{\hat n}^\mu} = {{\hat \nabla}^\mu}\ell\) and \({{\hat \ell}^\mu}{\partial _\mu} = {\partial _\ell}\) at \({{\mathcal I}^ +}\). Then the radiation is described by the limit
which corresponds in Newman-Penrose notation to \(- (1/2)\bar \psi _4^0\). The main calculational result in [14] is that
which is independent of the freedom \({{\hat m}^\mu} \rightarrow {{\hat m}^\mu} + \lambda {{\hat n}^\mu}\) in the choice of mμ. In inertial Bondi coordinates, this reduces to
which is related to the Bondi news function by
so that
with NΨ = N up to numerical error.
As in the case of the news function, the general expression (58) for \({\hat \Psi}\) must be used. This challenges numerical accuracy due to the large number of terms and the appearance of third angular derivatives. For instance, in the linearized approximation, the value of \({\hat \Psi}\) on \({{\mathcal I}^ +}\) is given by the fairly complicated expression
where J = QAQBhAB and L = QALA. In the same approximation, the news function is given by
(The relationship (60) still holds in the linearized approximation but in the nonlinear case, the derivative along the generators of \({{\mathcal I}^ +}\) is \({{\hat n}^\mu}{\partial _\mu} = {e^{- 2H}}({\partial _\mu} + {L^A}{\partial _A})\) and (60) must be modified accordingly.)
These linearized expressions provide a starting point to compare the advantages between computing the radiation via N or NΨ. The troublesome gauge terms involving L, H and ω all vanish in inertial Bondi coordinates (where ω = 1). One difference is that \({\hat \Psi}\) contains third order angular derivatives, e.g. \({\eth^3}\bar L\), as opposed to second angular derivatives for N. This means that the smoothness of the numerical error is more crucial in the \({\hat \Psi}\) approach. Balancing this, N contains the ð2ω term, which is a potential source of numerical error since ω must be evolved via (56).
The accuracy of waveform extraction via the Bondi news function N and its counterpart NΨ constructed from the Weyl curvature has been compared in a linearized gravitational wave test problem [14]. The results show that both methods are competitive, although the Ψ4 approach has an edge.
However, even though both methods were tested to be second order convergent, there was still considerable error, of the order of 5% for grids of practical size. This error reflects the intrinsic difficulty in extracting waveforms because of the delicate cancellation of leading order terms in the underlying metric and connection when computing the O(1/r) radiation field. It is somewhat analogous to the experimental task of isolating a transverse radiation field from the longitudinal fields representing the total mass, while in a very non-inertial laboratory. In the linearized wave test carried out in [14], the news consisted of the sum of three terms, N = A + B + C, where because of cancellations N ≈ A/24. The individual terms A, B and C had small fractional error but the cancellations magnified the fractional error in N.
The tests in [14] were carried out with a characteristic code using the circular-stereographic patches. The results are in qualitative agreement with tests of CCE using a cubed-sphere code [201], which in addition confirmed the expectation that fourth-order finite difference approximations for the ð-operator gives improved accuracy. As demonstrated recently [111], once all the necessary infrastructure for interpatch communication is in place, an advantage of the cubed-sphere approach is that its shared boundaries admit a highly scalable algorithm for parallel architectures.
Another alternative is to carry out a coordinate transformation in the neighborhood of \({{\mathcal I}^ +}\) to inertial Bondi coordinates, in which the news calculation is then quite clean numerically. This approach was implemented in [41] and shown to be second order convergent in Robinson-Trautman and Schwarzschild testbeds. However, it is clear that this coordinate transformation also involves the same difficult numerical problem of extracting a small radiation field in the presence of the large gauge effects that are present in the primary output data.
These underlying gauge effects which complicate CCE are introduced at the inner extraction worldtube and then propagate out to \({{\mathcal I}^ +}\). Perturbative waveform extraction suffers the same problem. Lehner and Moreschi [167] have shown that the delicate issues involved at \({{\mathcal I}^ +}\) have counterparts in Ψ4 extraction of radiation on a finite worldtube. They show that some of the techniques used at \({{\mathcal I}^ +}\) can also be used to reduce the effect of some of these ambiguities, in particular the ambiguity arising from the conformal factor ω. The analogue of ω on a finite worldtube can eliminate some of the non-inertial effects that might enter the radiation waveform. In addition, use of normalization conventions on the null tetrad defining Ψ4 analogous to the conventions at \({{\mathcal I}^ +}\) can avoid other spurious errors. This approach can also be used to correct gauge ambiguities in the calculation of momentum recoil in the merger of black holes [103].
7 Numerical Hydrodynamics on Null Cones
Numerical evolution of relativistic hydrodynamics has been traditionally carried out on spacelike Cauchy hypersurfaces. Although the Bondi-Sachs evolution algorithm can easily be extended to include matter [153], the advantage of a light cone approach for treating fluids is not as apparent as for a massless field whose physical characteristics lie on the light cone. However, results from recent studies of relativistic stars and of fluid sources moving in the vicinity of a black hole indicate that this approach can provide accurate simulations of astrophysical relevance such as supernova collapse to a black hole, mass accretion, and the production of gravitational waves.
7.1 Spherically symmetric hydrodynamic codes
The earliest fully general relativistic simulations of fluids were carried out in spherical symmetry. The first major work was a study of gravitational collapse by May and White [173]. Most of this early work was carried out using Cauchy evolution [91]. Miller and Mota [174] performed the first simulations of spherically symmetric gravitational collapse using a null foliation. Baumgarte, Shapiro and Teukolsky subsequently used a null slicing to study supernovae [33] and the collapse of neutron stars to form black holes [34]. The use of a null slicing allowed them to evolve the exterior spacetime while avoiding the region of singularity formation.
Barreto’s group in Venezuela applied characteristic methods to study the self-similar collapse of spherical matter and charge distributions [20, 24, 21]. The assumption of self-similarity reduces the problem to a system of ODE’s, subject to boundary conditions determined by matching to an exterior Reissner-Nordström-Vaidya solution. Heat flow in the internal fluid is balanced at the surface by the Vaidya radiation. Their simulations illustrate how a nonzero total charge can halt gravitational collapse and produce a final stable equilibrium [21]. It is interesting that the pressure vanishes in the final equilibrium state so that hydrostatic support is completely supplied by Coulomb repulsion.
Font and Papadopoulos [184] have given a state-of-the-art treatment of relativistic fluids which is applicable to either spacelike or null foliations. Their approach is based upon a high-resolution shock-capturing (HRSC) version of relativistic hydrodynamics in flux conservative form, which was developed by the Valencia group (for a review see [91]). In the HRSC scheme, the hydrodynamic equations are written in flux conservative, hyperbolic form. In each computational cell, the system of equations is diagonalized to determine the characteristic fields and velocities, and the local Riemann problem is solved to obtain a solution consistent with physical discontinuities. This allows a finite differencing scheme along the characteristics of the fluid that preserves the conserved physical quantities and leads to a stable and accurate treatment of shocks. Because the general relativistic system of hydrodynamical equations is formulated in covariant form, it can equally well be applied to spacelike or null foliations of the spacetime. The null formulation gave remarkable performance in the standard Riemann shock tube test carried out in a Minkowski background. The code was successfully implemented first in the case of spherical symmetry, using a version of the Bondi-Sachs formalism adapted to describe gravity coupled to matter with a worldtube boundary [237]. They verified second order convergence in curved space tests based upon Tolman-Oppenheimer-Volkoff equilibrium solutions for spherical fluids. In the dynamic self-gravitating case, simulations of spherical accretion of a fluid onto a black hole were stable and free of numerical problems. Accretion was successfully carried out in the regime where the mass of the black hole doubled. Subsequently the code was used to study how accretion modulates both the decay rates and oscillation frequencies of the quasi-normal modes of the interior black hole [185].
The characteristic hydrodynamic approach of Font and Papadopoulos was first applied to spherical symmetric problems of astrophysical interest. Linke, Font, Janka, Müller, and Papadopoulos [169] simulated the spherical collapse of supermassive stars, using an equation of state that included the effects due to radiation, electron-positron pair formation, and neutrino emission. They were able to follow the collapse from the onset of instability to black hole formation. The simulations showed that collapse of a star with mass greater than 5 × 105 solar masses does not produce enough radiation to account for the gamma ray bursts observed at cosmological redshifts.
Next, Siebel, Font, and Papadopoulos [222] studied the interaction of a massless scalar field with a neutron star by means of the coupled Klein-Gordon-Einstein-hydrodynamic equations. They analyzed the nonlinear scattering of a compact ingoing scalar pulse incident on a spherical neutron star in an initial equilibrium state obeying the null version of the Tolman-Oppenheimer-Volkoff equations. Depending upon the initial mass and radius of the star, the scalar field either excites radial pulsation modes or triggers collapse to a black hole. The transfer of scalar energy to the star was found to increase with the compactness of the star. The approach included a compactification of null infinity, where the scalar radiation was computed. The scalar waveform showed quasi-normal oscillations before settling down to a late time power law decay in good agreement with the t−3 dependence predicted by linear theory. Global energy balance between the star’s relativistic mass and the scalar energy radiated to infinity was confirmed.
7.2 Axisymmetric characteristic hydrodynamic simulations
The approach initiated by Font and Papadopoulos has been applied in axisymmetry to pioneering studies of gravitational waves from relativistic stars. The gravitational field is treated by the original Bondi formalism using the axisymmetric code developed by Papadopoulos [186, 120]. Because of the twist-free property of the axisymmetry in the original Bondi formalism, the fluid motion cannot have a rotational component about the axis of symmetry, i.e. the fluid velocity is constrained to the (r, θ) plane. In his thesis work, Siebel [219] extensively tested the combined hydrodynamic-gravity code in the nonlinear, relativistic regime and demonstrated that it accurately and stably maintained the equilibrium of a neutron star.
As a first application of the code, Siebel, Font, Müller, and Papadopoulos [220] studied axisymmetric pulsations of neutron stars, which were initiated by perturbing the density and θ-component of velocity of a spherically symmetric equilibrium configuration. The frequencies measured for the radial and non-radial oscillation modes of the star were found to be in good agreement with the results from linearized perturbation studies. The Bondi news function was computed and its amplitude found to be in rough agreement with the value given by the Einstein quadrupole formula. Both computations involve numerical subtleties: The computation of the news involves large terms which partially cancel to give a small result, and the quadrupole formula requires computing three time derivatives of the fluid variables. These sources of computational error, coupled with ambiguity in the radiation content in the initial data, prevented any definitive conclusions. The total radiated mass loss was approximately 10−9 of the total mass.
Next, the code was applied to the simulation of axisymmetric supernova core collapse [221]. A hybrid equation of state was used to mimic stiffening at collapse to nuclear densities and shock heating during the bounce. The initial equilibrium state of the core was modeled by a polytrope with index Γ = 4/3. Collapse was initiated by reducing the polytropic index to 1.3. In order to break spherical symmetry, small perturbations were introduced into the θ-component of the fluid velocity. During the collapse phase, the central density increased by 5 orders of magnitude. At this stage the inner core bounced at supra-nuclear densities, producing an expanding shock wave which heated the outer layers. The collapse phase was well approximated by spherical symmetry but non-spherical oscillations were generated by the bounce. The resulting gravitational waves at null infinity were computed by the compactified code. After the bounce, the Bondi news function went through an oscillatory build up and then decayed in an ℓ = 2 quadrupole mode. However, a comparison with the results predicted by the Einstein quadrupole formula no longer gave the decent agreement found in the case of neutron star pulsations. This discrepancy was speculated to be due to the relativistic velocities of ≈ 0.2c reached in the core collapse as opposed to 10−4c for the pulsations. However, gauge effects and numerical errors also make important contributions which cloud any definitive interpretation. This is the first study of gravitational wave production by the gravitational collapse of a relativistic star carried out with a characteristic code. It is clearly a remarkable piece of work which offers up a whole new approach to the study of gravitational waves from astrophysical sources.
7.3 Three-dimensional characteristic hydrodynamic simulations
The PITT code has been coupled with a rudimentary matter source to carry out three-dimensional characteristic simulations of a relativistic star orbiting a black hole. A naive numerical treatment of the Einstein-hydrodynamic system for a perfect fluid was incorporated into the code [47], but a more accurate HRSC hydrodynamic algorithm has not yet been implemented. The fully nonlinear matter-gravity null code was tested for stability and accuracy to verify that nothing breaks down as long as the fluid remains well behaved, e.g., hydrodynamic shocks do not form. The code was used to simulate a localized blob of matter falling into a black hole, verifying that the motion of the center of the blob approximates a geodesic and determining the waveform of the emitted gravitational radiation at \({{\mathcal I}^ +}\). This simulation was a prototype of a neutron star orbiting a black hole, although it would be unrealistic to expect that this naive treatment of the fluid could reliably evolve a compact star for several orbits. A 3D HRSC characteristic hydrodynamic code would open the way to explore this important astrophysical problem.
Short term issues were explored with the code in subsequent work [48]. The code was applied to the problem of determining realistic initial data for a star in circular orbit about a black hole. In either a Cauchy or characteristic approach to this initial data problem, a serious source of physical ambiguity is the presence of spurious gravitational radiation in the gravitational data. Because the characteristic approach is based upon a retarded time foliation, the resulting spurious outgoing waves can be computed by carrying out a short time evolution. Two very different methods were used to prescribe initial gravitational null data:
-
1.
a Newtonian correspondence method, which guarantees that the Einstein quadrupole formula is satisfied in the Newtonian limit [249], and
-
2.
setting the shear of the initial null hypersurface to zero.
Both methods are mathematically consistent but suffer from physical shortcomings. Method 1 has only approximate validity in the relativistic regime of a star in close orbit about a black hole while Method 2 completely ignores the gravitational lensing effect of the star. It was found that, independently of the choice of initial gravitational data, the spurious waves quickly radiate away, and that the system relaxes to a quasi-equilibrium state with an approximate helical symmetry corresponding to the circular orbit of the star. The results provide justification of recent approaches for initializing the Cauchy problem which are based on imposing an initial helical symmetry, as well as providing a relaxation scheme for obtaining realistic characteristic data.
7.3.1 Massive particle orbiting a black hole
One attractive way to avoid the computational expense of hydrodynamics in treating a star orbiting a massive black hole is to treat the star as a particle. This has been attempted using the PITT code to model a star of mass m orbiting a black hole of much larger mass, say 1000m [44]. The particle was described by the perfect fluid energy-momentum tensor of a rigid Newtonian polytrope in spherical equilibrium of a fixed size in its local proper rest frame, with its center following a geodesic. The validity of the model requires that the radius of the polytrope be large enough so that the assumption of Newtonian equilibrium is valid but small enough so that the assumption of rigidity is consistent with the tidal forces produced by the black hole. Characteristic initial gravitational data for a double null initial value problem were taken to be Schwarzschild data for the black hole. The system was then evolved using a fully nonlinear characteristic code. The evolution equations for the particle were arranged to take computational advantage of the energy and angular momentum conservation laws which would hold in the test body approximation.
The evolution was robust and could track the particle for two orbits as it spiraled into the black hole. Unfortunately, the computed rate of inspiral was much too large to be physically realistic: the energy loss was ≈ 103 greater than the value expected from perturbation theory. This discrepancy might have a physical origin, due to the choice of initial gravitational data that ignores the particle or due to a breakdown of the rigidity assumption, or a numerical origin due to improper resolution of the particle. It is a problem whose resolution would require the characteristic AMR techniques being developed [197].
These sources of error can be further aggravated by the introduction of matter fields, as encountered in trying to make definitive comparisons between the Bondi news and the Einstein quadrupole formula in the axisymmetric studies of supernova collapse [221] described in Section 7.2. In the three-dimensional characteristic simulations of a star orbiting a black hole [48, 44], the lack of resolution introduced by a localized star makes an accurate calculation of the news highly problematical. There exists no good testbed for validating the news calculation in the presence of a fluid source. A perturbation analysis in Bondi coordinates of the oscillations of an infinitesimal fluid shell in a Schwarzschild background [40] might prove useful for testing constraint propagation in the presence of a fluid. However, the underlying Fourier mode decomposition requires the gravitational field to be periodic so that the solution cannot be used to test computation of mass loss or radiation reaction effects.
References
Abrahams, A.M., and Evans, C.R., “Gauge-invariant treatment of gravitational radiation near the source: Analysis and numerical simulations”, Phys. Rev. D, 42, 2585–2594, (1990). [DOI], [ADS]. 1, 5.4
Abrahams, A.M., and Price, R.H., “Applying black hole perturbation theory to numerically generated spacetimes”, Phys. Rev. D, 53, 1963–1971, (1996). [DOI], [ADS]. 1, 5.4
Abrahams, A.M., Rezzolla, L., Rupright, M.E., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Cook, G.B., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Gómez, R., Haupt, T., Huq, M.F., Kidder, L.E., Klasky, S.A., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Saied, F., Saylor, P.E., Scheel, M.A., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Gravitational Wave Extraction and Outer Boundary Conditions by Perturbative Matching”, Phys. Rev. Lett., 80, 1812–1815, (1998). [DOI], [ADS]. 1, 5.4
Abrahams, A.M., Shapiro, S.L., and Teukolsky, S.A., “Calculation of gravitational waveforms from black hole collisions and disk collapse: Applying perturbation theory to numerical spacetimes”, Phys. Rev. D, 51, 4295–4301, (1995). [DOI], [ADS]. 1, 5.4
Alcubierre, M., Allen, G., Bona, C., Fiske, D., Goodale, T., Guzmán, F.S., Hawke, I., Hawley, S.H., Husa, S., Koppitz, M., Lechner, C., Pollney, D., Rideout, D., Salgado, M., Schnetter, E., Seidel, E., Shinkai, H.-a., Shoemaker, D., Szilágyi, B., Takahashi, R., and Winicour, J., “Towards standard testbeds for numerical relativity”, Class. Quantum Grav., 21, 589–613, (2004). [DOI], [ADS]. 4.2.4
Anderson, J.L., “Gravitational radiation damping in systems with compact components”, Phys. Rev. D, 36, 2301–2313, (1987). [DOI], [ADS]. 5.4
Anderson, J.L., and Hobill, D.W., “Matched analytic-numerical solutions of wave equations”, in J.M., Centrella., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of the Workshop held at Drexel University, October 7–11, 1985, pp. 389–410, (Cambridge University Press, Cambridge, New York, 1986). [ADS]. 5.4
Anderson, J.L., and Hobill, D.W., “Mixed analytic-numerical solutions for a simple radiating system”, Gen. Relativ. Gravit., 19, 563–580, (1987). [DOI], [ADS]. 5.4
Anderson, J.L., and Hobill, D.W., “A study of nonlinear radiation damping by matching analytic and numerical solutions”, J. Comput. Phys., 75, 283–299, (1988). [DOI], [ADS]. 5.4
Anderson, J.L., Kates, R.E., Kegeles, L.S., and Madonna, R.G., “Divergent integrals of post-Newtonian gravity: Nonanalytic terms in the near-zone expansion of a gravitationally radiating system found by matching”, Phys. Rev. D, 25, 2038–2048, (1982). [DOI], [ADS]. 5.4
Anninos, P., Daues, G., Massó, J., Seidel, E., and Suen, W.-M., “Horizon boundary conditions for black hole spacetimes”, Phys. Rev. D, 51, 5562–5578, (1995). [DOI], [ADS]. 5.5.3
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, pp. 227–265, (Wiley, New York, 1962). [DOI], [ADS]. 5
Babiuc, M., Szilágyi, B., Hawke, I., and Zlochower, Y., “Gravitational wave extraction based on Cauchy-characteristic extraction and characteristic evolution”, Class. Quantum Grav., 22, 5089–5107, (2005). [DOI], [ADS]. 5.4
Babiuc, M.C., Bishop, N.T., Szilágyi, B., and Winicour, J., “Strategies for the characteristic extraction of gravitational waveforms”, arXiv e-print, (2008). [arXiv:0808.0861]. 4.2.1, 6, 6, 6
Babiuc, M.C., Husa, S., Alic, D., Hinder, I., Lechner, C., Schnetter, E., Szilágyi, B., Zlochower, Y., Dorband, N., Pollney, D., and Winicour, J., “Implementation of standard testbeds for numerical relativity”, Class. Quantum Grav., 25, (125012), 1–38, (2008). [DOI], [ADS]. 5
Babiuc, M.C., Kreiss, H.-O., and Winicour, J., “Constraint-preserving Sommerfeld conditions for the harmonic Einstein equations”, Phys. Rev. D, 75, (044002), 1–13, (2007). [DOI], [ADS]. 5.3
Baker, J., Campanelli, M., Lousto, C.O., and Takahashi, R., “Modeling gravitational radiation from coalescing binary black holes”, Phys. Rev. D, 65, 124012, 23, (2002). [DOI], [ADS]. 6
Baker, J.G., Centrella, J., Choi, D.-I., Koppitz, M., and van Meter, J., “Binary black hole merger dynamics and waveforms”, Phys. Rev. D, 73, (104002), 1–11, (2006). [DOI], [ADS]. 6
Baker, J.G., Centrella, J., Choi, D.-I., Koppitz, M., and van Meter, J., “Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes”, Phys. Rev. Lett., 96, 111102, (2006). [DOI], [ADS]. 1
Barreto, W., and Da Silva, A., “Gravitational collapse of a charged and radiating fluid ball in the diffusion limit”, Gen. Relativ. Gravit., 28, 735–747, (1996). [DOI], [ADS]. 7.1
Barreto, W., and Da Silva, A., “Self-similar and charged spheres in the diffusion approximation”, Class. Quantum Grav., 16, 1783–1792, (1999). [DOI], [ADS]. 7.1
Barreto, W., Da Silva, A., Gómez, R., Lehner, L., Rosales, L., and Winicour, J., “Three-dimensional Einstein-Klein-Gordon system in characteristic numerical relativity”, Phys. Rev. D, 71, (064028), 1–12, (2005). [DOI], [ADS]. 4.6
Barreto, W., Gómez, R., Lehner, L., and Winicour, J., “Gravitational instability of a kink”, Phys. Rev. D, 54, 3834–3839, (1996). [DOI], [ADS]. 3.1
Barreto, W., Peralta, C., and Rosales, L., “Equation of state and transport processes in self-similar spheres”, Phys. Rev. D, 59, (024008), 1–4, (1998). [ADS]. 7.1
Bartnik, R., “Einstein equations in the null quasispherical gauge”, Class. Quantum Grav., 14, 2185–2194, (1997). [DOI], [ADS]. 4.2
Bartnik, R., “Shear-free null quasi-spherical space-times”, J. Math. Phys., 38, 5774–5791, (1997). [DOI], [ADS]. 4.2
Bartnik, R., “Interaction of gravitational waves with a black hole”, in De Wit, D., Bracken, A.J., Gould, M.D., and Pearce, P.A., eds., XIIth International Congress of Mathematical Physics (ICMP 1997), Proceedings of the Congress held at the University of Queensland, Brisbane, Australia, July 1997, p. 3, (International Press, Somerville, 1999). 3.4, 4.2.5, 4.2.6
Bartnik, R., “Assessing accuracy in a numerical Einstein solver”, in Weinstein, G., and Weikard, R., eds., Differential Equations and Mathematical Physics, Proceedings of an international conference held at the University of Alabama in Birmingham, March 16–20, 1999, AMS/IP Studies in Advanced Mathematics, vol. 16, p. 11, (American Mathematical Society; International Press, Providence, 2000). 4.2.4
Bartnik, R., and Norton, A.H., “Numerical solution of the Einstein equations”, in Noye, B.J., Teubner, M.D., and Gill, A.W., eds., Computational Techniques and Applications: CTAC97, p. 91, (World Scientific, Singapore, 1998). 4.2.4
Bartnik, R., and Norton, A.H., “Numerical Methods for the Einstein Equations in Null Quasi-Spherical Coordinates”, SIAM J. Sci. Comput., 22, 917–950, (2000). [DOI]. 3.4, 3.4, 4.1, 4.1.3, 4.2.4
Bartnik, R., and Norton, A.H., “Numerical Experiments at Null Infinity”, in Friedrich, H., and Frauendiener, J., eds., The Conformal Structure of Space-Time: Geometry, Analysis, Numerics, Proceedings of the international workshop, Tübingen, Germany, 2–4 April 2001, Lecture Notes in Physics, vol. 604, pp. 313–326, (Springer, Berlin; New York, 2002). [ADS]. 4.2.6
Baumgarte, T.W., and Shapiro, S.L., “Numerical integration of Einstein’s field equations”, Phys. Rev. D, 59, (024007), 1–7, (1998). [DOI], [ADS]. 1
Baumgarte, T.W., Shapiro, S.L., and Teukolsky, S.A., “Computing Supernova Collapse to Neutron Stars and Black Holes”, Astrophys. J., 443, 717–734, (1995). [DOI], [ADS]. 7.1
Baumgarte, T.W., Shapiro, S.L., and Teukolsky, S.A., “Computing the Delayed Collapse of Hot Neutron Stars to Black Holes”, Astrophys. J., 458, 680–691, (1996). [DOI], [ADS]. 7.1
Bayliss, A., and Turkel, E., “Radiation boundary conditions for wavelike equations”, Commun. Pure Appl. Math., 33, 707–725, (1980). [DOI], [ADS]. 5.1
Berger, B.K., “Numerical Approaches to Spacetime Singularities”, Living Rev. Relativity, 5, lrr-2002-1, (2002). URL (cited on 20 July 2005): http://www.livingreviews.org/lrr-2002-1. 3.1
Bičák, J., Reilly, P., and Winicour, J., “Boost-rotation symmetric gravitational null cone data”, Gen. Relativ. Gravit., 20, 171–181, (1988). [DOI], [ADS]. 4.2.5, 5.6
Bishop, N.T., “Some aspects of the characteristic initial value problem in numerical relativity”, in d’Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, pp. 20–33, (Cambridge University Press, Cambridge; New York, 1992). [ADS]. 5.2
Bishop, N.T., “Numerical relativity: combining the Cauchy and characteristic initial value problems”, Class. Quantum Grav., 10, 333–341, (1993). [DOI], [ADS]. 5, 5.2
Bishop, N.T., “Linearized solutions of the Einstein equations within a Bondi-Sachs framework, and implications for boundary conditions in numerical simulations”, Class. Quantum Grav., 22, 2393–2406, (2005). [DOI], [ADS]. 4.2.5, 7.3.1
Bishop, N.T., and Deshingkar, S.S., “New approach to calculating the news”, Phys. Rev. D, 68, (024031), 1–6, (2003). [DOI], [ADS]. 6
Bishop, N.T., Gómez, R., Holvorcem, P.R., Matzner, R.A., Papadopoulos, P., and Winicour, J., “Cauchy-Characteristic Matching: A New Approach to Radiation Boundary Conditions”, Phys. Rev. Lett., 76, 4303–4306, (1996). [DOI], [ADS]. 5.2, 5.7
Bishop, N.T., Gómez, R., Holvorcem, P.R., Matzner, R.A., Papadopoulos, P., and Winicour, J., “Cauchy-Characteristic Evolution and Waveforms”, J. Comput. Phys., 136, 140–167, (1997). [DOI], [ADS]. Erratum J. Comput. Phys., 148, 299–301, (1997), DOI:10.1006/jcph.1998.6139. 5.1, 5.2, 5.7
Bishop, N.T., Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Numerical relativistic model of a massive particle in orbit near a Schwarzschild black hole”, Phys. Rev. D, 68, (084015), 1–12, (2003). [DOI], [ADS]. 6, 7.3.1
Bishop, N.T., Gómez, R., Isaacson, R.A., Lehner, L., Szilágyi, B., and Winicour, J., “Cauchy-characteristic matching”, in Bhawal, B., and Iyer, B.R., eds., Black Holes, Gravitational Radiation and the Universe: Essays in Honour of C. V. Vishveshwara, Fundamental Theories of Physics, pp. 383–408, (Kluwer, Dordrecht; Boston, 1999). [ADS]. 5.2, 5.8
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “High-powered gravitational news”, Phys. Rev. D, 56, 6298–6309, (1997). [DOI], [ADS]. 4, 4.2.4, 4.2.5, 5.9, 6
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “The incorporation of matter into characteristic numerical relativity”, Phys. Rev. D, 60, (024005), 1–11, (1999). [DOI], [ADS]. 7.3
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “Characteristic initial data for a star orbiting a black hole”, Phys. Rev. D, 72, (024002), 1–16, (2005). [DOI], [ADS]. 4.6, 7.3, 7.3.1
Bishop, N.T., Gómez, R., Lehner, L., and Winicour, J., “Cauchy-characteristic extraction in numerical relativity”, Phys. Rev. D, 54, 6153–6165, (1996). [DOI], [ADS]. 4, 4.2, 4.2.4, 4.2.5, 5.2, 5.4
Bishop, N.T., and Venter, L.R., “Kerr metric in Bondi-Sachs form”, Phys. Rev. D, 73, (084023), 1–6, (2006). [DOI], [ADS]. 4.2.7
Bizoń, P., “Equivariant Self-Similar Wave Maps from Minkowski Spacetime into 3-Sphere”, Commun. Math. Phys., 215, 45–56, (2000). [DOI], [ADS]. 3.1
Blaschak, J.G., and Kriegsmann, G.A., “A comparative study of absorbing boundary conditions”, J. Comput. Phys., 77, 109–139, (1988). [DOI], [ADS]. 5.1
Bondi, H., “Gravitational waves in general relativity”, Nature, 186, 535–535, (1960). [DOI], [ADS]. 1, 2
Bondi, H., van derBurg, M.G.J., and Metzner, A.W.K., “Gravitational Waves in General Relativity. VII. Waves from Axi-Symmetric Isolated Systems”, Proc. R. Soc. London, Ser. A, 269, 21–52, (1962). [DOI], [ADS]. 1, 2, 3.3, 3.3
Brady, P.R., Chambers, C.M., and Gonçalves, S.M.C.V., “Phases of massive scalar field collapse”, Phys. Rev. D, 56, R6057–R6061, (1997). [DOI], [ADS]. 3.1
Brady, P.R., Chambers, C.M., Krivan, W., and Laguna, P., “Telling tails in the presence of a cosmological constant”, Phys. Rev. D, 55, 7538–7545, (1997). [DOI], [ADS]. 3.1
Brady, P.R., and Smith, J.D., “Black Hole Singularities: A Numerical Approach”, Phys. Rev. Lett., 75, 1256–1259, (1995). [DOI], [ADS]. 3.1
Browning, G.L., Hack, J.J., and Swarztrauber, P.N., “A Comparison of Three Numerical Methods for Solving Differential Equations on the Sphere”, Mon. Weather Rev., 117, 1058–1075, (1989). [DOI], [ADS]. 4.1, 4.1.1
Burke, W.L., “Gravitational Radiation Damping of Slowly Moving Systems Calculated Using Matched Asymptotic Expansions”, J. Math. Phys., 12, 401–418, (1971). [DOI], [ADS]. 5.4
Burko, L.M., “Structure of the Black Hole’s Cauchy-Horizon Singularity”, Phys. Rev. Lett., 79, 4958–4961, (1997). [DOI], [ADS]. 3.1, 3.1.1
Burko, L.M., and Ori, A., “Late-time evolution of nonlinear gravitational collapse”, Phys. Rev. D, 56, 7820–7832, (1997). [DOI], [ADS]. 3.1
Butler, D.S., “The Numerical Solution of Hyperbolic Systems of Partial Differential Equations in Three Independent Variables”, Proc. R. Soc. London, Ser. A, 255, 232–252, (1960). [DOI], [ADS]. 3.2
Calabrese, G., Lehner, L., and Tiglio, M., “Constraint-preserving boundary conditions in numerical relativity”, Phys. Rev. D, 65, (104031), 1–13, (2002). [DOI], [ADS]. 5.3
Calabrese, G., Pullin, J., Reula, O., Sarbach, O., and Tiglio, M., “Well Posed Constraint-Preserving Boundary Conditions for the Linearized Einstein Equations”, Commun. Math. Phys., 240, 377–395, (2003). [DOI], [ADS]. 5.3
Campanelli, M., Gómez, R., Husa, S., Winicour, J., and Zlochower, Y., “Close limit from a null point of view: The advanced solution”, Phys. Rev. D, 63, (124013), 1–15, (2001). [DOI], [ADS]. 4.4, 4.4, 4.4.1, 5.4
Campanelli, M., Lousto, C.O., Marronetti, P., and Zlochower, Y., “Accurate Evolutions of Orbiting Black-Hole Binaries without Excision”, Phys. Rev. Lett., 96, 111101, (2006). [DOI], [ADS]. 1, 6
Choptuik, M.W., “‘Critical’ behavior in massless scalar field collapse”, in d’Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, p. 202, (Cambridge University Press, Cambridge; New York, 1992). [ADS]. 3.1
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70, 9–12, (1993). [DOI], [ADS]. 3.1, 5.5.2
Christodoulou, D., “A mathematical theory of gravitational collapse”, Commun. Math. Phys., 109, 613–647, (1987). [DOI], [ADS]. 3.1
Christodoulou, D., “The formation of black holes and singularities in spherically symmetric gravitational collapse”, Commun. Pure Appl. Math., 44, 339–373, (1991). [DOI]. 3.1
Christodoulou, D., “Bounded Variation Solutions of the Spherically Symmetric Einstein-Scalar Field Equations”, Commun. Pure Appl. Math., 46, 1131–1220, (1993). [DOI]. 3.1
Christodoulou, D., “Examples of Naked Singularity Formation in the Gravitational Collapse of a Scalar Field”, Ann. Math. (2), 140, 607–653, (1994). 3.1
Christodoulou, D., “The Instability of Naked Singularities in the Gravitational Collapse of a Scalar Field”, Ann. Math. (2), 149, 183–217, (1999). 3.1
Christodoulou, D., “On the global initial value problem and the issue of singularities”, Class. Quantum Grav., 16, A23–A35, (1999). [DOI], [ADS]. 3.1
Christodoulou, D., and Klainerman, S., The Global Nonlinear Stability of the Minkowski Space, Princeton Mathematical Series, vol. 41, (Princeton University Press, Princeton, 1993). 3.3
Clarke, C.J.S., and d’Inverno, R.A., “Combining Cauchy and characteristic numerical evolutions in curved coordinates”, Class. Quantum Grav., 11, 1463–1448, (1994). [DOI], [ADS]. 5.2, 5.5.1
Clarke, C.J.S., d’Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. I. The vacuum cylindrically symmetric problem”, Phys. Rev. D, 52, 6863–6867, (1995). [DOI], [ADS]. 3.1, 5.2, 5.5.1
Cook, G.B., Huq, M.F., Klasky, S.A., Scheel, M.A., Abrahams, A.M., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Gómez, R., Haupt, T., Kidder, L.E., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Rezzolla, L., Rupright, M.E., Saied, F., Saylor, P.E., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Suen, W-M., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (Binary Black Hole Grand Challenge Alliance), “Boosted Three-Dimensional Black-Hole Evolutions with Singularity Excision”, Phys. Rev. Lett., 80, 2512–2516, (1998). [DOI], [ADS]. 3.3
Corkill, R.W., and Stewart, J.M., “Numerical Relativity. II. Numerical Methods for the Characteristic Initial Value Problem and the Evolution of the Vacuum Field Equations for Space-Times with Two Killing Vectors”, Proc. R. Soc. London, Ser. A, 386, 373–391, (1983). [DOI], [ADS]. 2, 3.1
de Moerloose, J., and de Zutter, D., “Surface integral representation radiation boundary condition for the FDTD method”, IEEE Trans. Ant. Prop., 41, 890–896, (1993). [DOI], [ADS]. 5.1
de Oliveira, H.P., and Rodrigues, E.L., “A Galerkin approach for the Bondi problem”, arXiv e-print, (2008). [arXiv:0809.2837]. 3.3.3
Derry, L., Isaacson, R.A., and Winicour, J., “Shear-Free Gravitational Radiation”, Phys. Rev., 185, 1647–1655, (1969). [DOI], [ADS]. 4.2
d’Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, (Cambridge University Press, Cambridge; New York, 1992). 2
d’Inverno, R.A., Dubal, M.R., and Sarkies, E.A., “Cauchy-characteristic matching for a family of cylindrical solutions possessing both gravitational degrees of freedom”, Class. Quantum Grav., 17, 3157–3170, (2000). [DOI], [ADS]. 5.5.1
d’Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. III. The interface problem in axial symmetry”, Phys. Rev. D, 54, 4919–4928, (1996). [DOI], [ADS]. 3.3.4, 5.6
d’Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. IV. The characteristic field equations in axial symmetry”, Phys. Rev. D, 56, 772–784, (1997). [DOI], [ADS]. 3.3.4, 5.6
Dubal, M.R., d’Inverno, R.A., and Clarke, C.J.S., “Combining Cauchy and characteristic codes. II. The interface problem for vacuum cylindrical symmetry”, Phys. Rev. D, 52, 6868–6881, (1995). [DOI], [ADS]. 3.1, 5.2, 5.5.1
Duff, G.F.D., “Mixed problems for linear systems of first order equations”, Can. J. Math., 10, 127–160, (1958). 4.2.2, 5.2
Engquist, B., and Majda, A., “Absorbing Boundary Conditions for the Numerical Simulation of Waves”, Math. Comput., 31(139), 629–651, (1977). [ADS]. 5.1
Fletcher, S.J., and Lun, A.W.C., “The Kerr spacetime in generalized Bondi-Sachs coordinates”, Class. Quantum Grav., 20, 4153–4167, (2003). [DOI], [ADS]. 4.2.7
Font, J.A., “Numerical Hydrodynamics in General Relativity”, Living Rev. Relativity, 11, lrr-2008-7, (2008). URL (cited on 03 October 2008): http://www.livingreviews.org/lrr-2008-7. 1, 7.1
Frauendiener, J., “Conformal Infinity”, Living Rev. Relativity, 7, lrr-2004-1, (2004). URL (cited on 20 October 2005): http://www.livingreviews.org/lrr-2004-1. 2
Friedman, J.L., Schleich, K., and Witt, D.M., “Topological Censorship”, Phys. Rev. Lett. 71, 1486–1489, (1993). [DOI], [ADS]. 4.3
Friedrich, H., “The Asymptotic Characteristic Initial Value Problem for Einstein’s Vacuum Field Equations as an Initial Value Problem for a First-Order Quasilinear Symmetric Hyperbolic System”, Proc. R. Soc. London, Ser. A, 378, 401–421, (1981). [DOI], [ADS]. 3.3.1, 4.3
Friedrich, H., “On the regular and the asymptotic characteristic initial value problem for Einstein’s vacuum field equations”, Proc. R. Soc. London, Ser. A, 375, 169–184, (1981). [ADS]. 4.3
Friedrich, H., “Cauchy problems for the conformal vacuum field equations in general relativity”, Commun. Math. Phys., 91, 445–472, (1983). [DOI], [ADS]. 2
Friedrich, H., “Hyperbolic reductions for Einstein’s equations”, Class. Quantum Grav., 13, 1451–1469, (1996). [DOI], [ADS]. 5.3
Friedrich, H., and Nagy, G., “The Initial Boundary Value Problem for Einstein’s Vacuum Field Equation”, Commun. Math. Phys., 201, 619–655, (1999). [DOI], [ADS]. 5.3, 5.3
Friedrich, H., and Stewart, J.M., “Characteristic Initial Data and Wavefront Singularities in General Relativity”, Proc. R. Soc. London, Ser. A, 385, 345–371, (1983). [DOI], [ADS]. 1, 3.3.1
Frittelli, S., and Gómez, R., “Einstein boundary conditions for the 3+1 Einstein equations”, Phys. Rev. D, 68, (044014), 1–6, (2003). [DOI], [ADS]. 5.3
Frittelli, S., and Gómez, R., “Initial-boundary-value problem of the self-gravitating scalar field in the Bondi-Sachs gauge”, Phys. Rev. D, 75, (044021), 1–15, (2007). [DOI], [ADS]. 3.1
Frittelli, S., and Lehner, L., “Existence and uniqueness of solutions to characteristic evolution in Bondi-Sachs coordinates in general relativity”, Phys. Rev. D, 59, (084012), 1–9, (1999). [DOI], [ADS]. 4.2.2
Gallo, E., Lehner, L., and Moreschi, O.M., “Estimating total momentum at finite distances”, Phys. Rev. D, 78, (084027), 1–11, (2008). [DOI], [ADS]. 6
Garfinkle, D., “Choptuik scaling in null coordinates”, Phys. Rev. D, 51, 5558–5561, (1995). [DOI], [ADS]. 3.1, 3.1.1
Garfinkle, D., Cutler, C., and Duncan, G.C., “Choptuik scaling in six dimensions”, Phys. Rev. D, 60, (104007), 1–5, (1999). [DOI], [ADS]. 3.1
Geroch, R., “A Method for Generating Solutions of Einstein’s Equations”, J. Math. Phys., 12, 918–924, (1971). [DOI]. 3.1
Givoli, D., “Non-reflecting boundary conditions”, J. Comput. Phys., 94, 1–29, (1991). [DOI], [ADS]. 5.1
Gnedin, M.L., and Gnedin, N.Y., “Destruction of the Cauchy horizon in the Reissner-Nordström black hole”, Class. Quantum Grav., 10, 1083–1102, (1993). [DOI], [ADS]. 3.1
Goldwirth, D.S., and Piran, T., “Gravitational collapse of massless scalar field and cosmic censorship”, Phys. Rev. D, 36, 3575–3581, (1987). [DOI], [ADS]. 3.1, 4.2.3
Gómez, R., “Gravitational waveforms with controlled accuracy”, Phys. Rev. D, 64, (024007), 1–8, (2001). [DOI], [ADS]. 4.2.2
Gómez, R., Barreto, W., and Frittelli, S., “Framework for large-scale relativistic simulations in the characteristic approach”, Phys. Rev. D, 76, (124029), 1–22, (2007). [DOI], [ADS]. 4, 4.1.2, 4.2.3, 4.2.4, 4.6, 6
Gómez, R., and Frittelli, S., “First-order quasilinear canonical representation of the characteristic formulation of the Einstein equations”, Phys. Rev. D, 68, (084013), 1–6, (2003). [DOI], [ADS]. 4.2.2
Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Gravitational waves from a fissioning white hole”, Phys. Rev. D, 66, (064019), 1–8, (2002). [DOI], [ADS]. 4.2.2, 4.4.2
Gómez, R., Husa, S., and Winicour, J., “Complete null data for a black hole collision”, Phys. Rev. D, 64, (024010), 1–20, (2001). [DOI], [ADS]. 4.3
Gómez, R., Laguna, P., Papadopoulos, P., and Winicour, J., “Cauchy-characteristic evolution of Einstein-Klein-Gordon systems”, Phys. Rev. D, 54, 4719–4727, (1996). [DOI], [ADS]. 5.5.2
Gómez, R., Lehner, L., Marsa, R.L., and Winicour, J., “Moving black holes in 3D”, Phys. Rev. D, 57, 4778–4788, (1998). [DOI], [ADS]. 2, 4, 4.2.4, 4.2.5, 4.2.7, 5.9
Gómez, R., Lehner, L., Marsa, R.L., Winicour, J., Abrahams, A.M., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Cook, G.B., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Haupt, T., Huq, M.F., Kidder, L.E., Klasky, S.A., Laguna, P., Landry, W., Lenaghan, J., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Rezzolla, L., Rupright, M.E., Saied, F., Saylor, P.E., Scheel, M.A., Seidel, E., Shapiro, S.L., Shoemaker, D., Smarr, L.L., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Stable characteristic evolution of generic three-dimensional single-black-hole spacetimes”, Phys. Rev. Lett., 80, 3915–3918, (1998). [DOI], [ADS]. 4.2.4
Gómez, R., Lehner, L., Papadopoulos, P., and Winicour, J., “The eth formalism in numerical relativity”, Class. Quantum Grav., 14, 977–990, (1997). [DOI], [ADS]. 4.1.1
Gómez, R., Marsa, R.L., and Winicour, J., “Black hole excision with matching”, Phys. Rev. D, 56, 6310–6319, (1997). [DOI], [ADS]. 4, 4.2.7, 5.5.3, 5.5.3, 5.9
Gómez, R., Papadopoulos, P., and Winicour, J., “Null cone evolution of axisymmetric vacuum space-times”, J. Math. Phys., 35, 4184–4204, (1994). [DOI], [ADS]. 1, 3.3, 4.2.4, 7.2
Gómez, R., Reilly, P., Winicour, J., and Isaacson, R.A., “Post-Newtonian behavior of the Bondi mass”, Phys. Rev. D, 47, 3292–3302, (1993). [DOI], [ADS]. 3.4
Gómez, R., and Winicour, J., “Asymptotics of gravitational collapse of scalar waves”, J. Math. Phys., 33, 1445–1457, (1992). [DOI], [ADS]. 3.1, 3.1
Gómez, R., and Winicour, J., “Gravitational wave forms at finite distances and at null infinity”, Phys. Rev. D, 45, 2776–2782, (1992). [DOI], [ADS]. 5.4
Gómez, R., Winicour, J., and Isaacson, R.A., “Evolution of scalar fields from characteristic data”, J. Comput. Phys., 98, 11–25, (1992). [DOI], [ADS]. 1
Gómez, R., Winicour, J., and Schmidt, B.G., “Newman-Penrose constants and the tails of self-gravitating waves”, Phys. Rev. D, 49, 2828–2836, (1994). [DOI], [ADS]. 3.1
Grote, M.J., and Keller, J.B., “Nonreflecting Boundary Conditions for Maxwell’s Equations”, J. Comput. Phys., 139, 327–342, (1998). [DOI]. 5.1
Gundlach, C., and Martín-García, J.M., “Critical Phenomena in Gravitational Collapse”, Living Rev. Relativity, 10, lrr-2007-5, (1999). URL (cited on 03 October 2008): http://www.livingreviews.org/lrr-2007-5. 3.1
Gundlach, C., and Martín-García, J.M., “Symmetric hyperbolicity and consistent boundary conditions for second-order Einstein equations”, Phys. Rev. D, 70, (044032), 1–16, (2004). [DOI], [ADS]. 5.3
Gundlach, C., Price, R.H., and Pullin, J., “Late-time behavior of stellar collapse and explosions. I. Linearized perturbations”, Phys. Rev. D, 49, 883–889, (1994). [DOI], [ADS]. 3.1
Gundlach, C., Price, R.H., and Pullin, J., “Late-time behavior of stellar collapse and explosions. II. Nonlinear evolution”, Phys. Rev. D, 49, 890–899, (1994). [DOI], [ADS]. 3.1
Gustafsson, B., and Kreiss, H.-O., “Boundary conditions for time dependent problems with an artificial boundary”, J. Comput. Phys., 30, 331–351, (1979). [DOI], [ADS]. 5.1
Gustafsson, B., Kreiss, H.-O., and Oliger, J., Time Dependent Problems and Difference Methods, (Wiley, New York, 1995). 5.1
Hagstrom, T., and Hariharan, S.I., “Accurate Boundary Conditions for Exterior Problems in Gas Dynamics”, Math. Comput., 51, 581–597, (1988). [ADS]. 5.1
Hamadé, R.S., Horne, J.H., and Stewart, J.M., “Continuous self-similarity and S-duality”, Class. Quantum Grav., 13, 2241–2253, (1996). [DOI], [ADS]. 3.1
Hamadé, R.S., and Stewart, J.M., “The spherically symmetric collapse of a massless scalar field”, Class. Quantum Grav., 13, 497–512, (1996). [DOI], [ADS]. 3.1, 3.1.1
Hayward, S.A., “Dual-null dynamics of the Einstein field”, Class. Quantum Grav., 10, 779–790, (1993). [DOI], [ADS]. 4.3
Hedstrom, G.W., “Nonreflecting boundary conditions for nonlinear hyperbolic systems”, J. Comput. Phys., 30, 222–237, (1979). [DOI], [ADS]. 5.1
Higdon, R.L., “Absorbing Boundary Conditions for Difference Approximations to the Multi-Dimensional Wave Equation”, Math. Comput., 47, 437–459, (1986). 5.1, 5.1
Hod, S., “High-order contamination in the tail gravitational collapse”, Phys. Rev. D, 60, (104053), 1–4, (1999). [DOI], [ADS]. 3.1
Hod, S., “Wave tails in non-trivial backgrounds”, Class. Quantum Grav., 18, 1311–1318, (2001). [DOI], [ADS]. 3.1
Hod, S., “Wave tails in time-dependent backgrounds”, Phys. Rev. D, 66, (024001), 1–4, (2002). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Critical behavior and universality in gravitational collapse of a charged scalar field”, Phys. Rev. D, 55, 3485–3496, (1997). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Late-time evolution of charged gravitational collapse and decay of charged scalar hair. I”, Phys. Rev. D, 58, (024017), 1–6, (1998). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Late-time evolution of charged gravitational collapse and decay of charged scalar hair. II”, Phys. Rev. D, 58, (024018), 1–6, (1998). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Late-time evolution of charged gravitational collapse and decay of charged scalar hair. III. Nonlinear analysis”, Phys. Rev. D, 58, (024019), 1–6, (1998). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Late-time tails in gravitational collapse of a self-interacting (massive) scalar-field and decay of a self-interacting scalar hair”, Phys. Rev. D, 58, (044018), 1–6, (1998). [DOI], [ADS]. 3.1
Hod, S., and Piran, T., “Mass Inflation in Dynamical Gravitational Collapse of a Charged Scalar Field”, Phys. Rev. Lett., 81, 1554–1557, (1998). [DOI], [ADS]. 3.1
Husa, S., “Numerical relativity with the conformal field equations”, in Fernádez-Jambrina, L., and González-Romero, L.M., eds., Current Trends in Relativistic Astrophysics: Theoretical, Numerical, Observational, Proceedings of the 24th Spanish Relativity Meeting on Relativistic Astrophysics, Madrid, 2001, Lecture Notes in Physics, vol. 617, pp. 159–192, (Springer, Berlin; New York, 2003). [ADS]. 2
Husa, S., Lechner, C., Pürrer, M., Thornburg, J., and Aichelburg, P.C., “Type II critical collapse of a self-gravitating nonlinear σ model”, Phys. Rev. D, 62, (104007), 1–11, (2000). [DOI], [ADS]. 3.1
Husa, S., and Winicour, J., “Asymmetric merger of black holes”, Phys. Rev. D, 60, (084019), 1–13, (1999). [DOI], [ADS]. 2, 4.3, 4.3
Husa, S., Zlochower, Y., Gómez, R., and Winicour, J., “Retarded radiation from colliding black holes in the close limit”, Phys. Rev. D, 65, (084034), 1–14, (2002). [DOI], [ADS]. 4.4, 4.4.1, 5.4
Ipser, J.R., and Horwitz, G., “The Problem of Maximizing Functionals in Newtonian Stellar Dynamics, and its Relation to Thermodynamic and Dynamical Stability”, Astrophys. J., 232(3), 863–873, (1979). [DOI], [ADS]. 3.1
Isaacson, R.A., Welling, J.S., and Winicour, J., “Null cone computation of gravitational radiation”, J. Math. Phys., 24, 1824–1834, (1983). [DOI], [ADS]. 3.3, 3.3, 3.4, 7
Israeli, M., and Orszag, S.A., “Approximation of radiation boundary conditions”, J. Comput. Phys., 41, 115–135, (1981). [DOI], [ADS]. 5.1, 5.1
Jiang, H., and Wong, Y.S., “Absorbing boundary conditions for second-order hyperbolic equations”, J. Comput. Phys., 88, 205–231, (1990). [DOI], [ADS]. 5.1
Kates, R.E., and Kegeles, L.S., “Nonanalytic terms in the slow-motion expansion of a radiating scalar field on a Schwarzschild background”, Phys. Rev. D, 25, 2030–2037, (1982). [DOI], [ADS]. 5.4
Khan, K.A., and Penrose, R., “Scattering of Two Impulsive Gravitational Plane Waves”, Nature, 229, 185–186, (1971). [DOI], [ADS]. 3.1
Kreiss, H.-O., and Oliger, J., Methods for the approximate solution of time dependent problems, GARP Publications Series, 10, (World Meteorological Organization (WMO), International Council of Scientific Unions (ICSU), Geneva, 1973). Global Atmospheric Research Programme. 4.2.1
Kreiss, H.-O., and Ortiz, O.E., “Some Mathematical and Numerical Questions Connected with First and Second Order Time-Dependent Systems of Partial Differential Equations”, in Frauendiener, J., and Friedrich, H., eds., The Conformal Structure of Space-Time: Geometry, Analysis, Numerics, Proceedings of the international workshop, Tübingen, Germany, 2–4 April 2001, Lecture Notes in Physics, vol. 604, pp. 359–370, (Springer, Berlin; New York, 2002). [DOI], [ADS]. 1, 4.2.2
Kreiss, H.-O., Reula, O., Sarbach, O., and Winicour, J., “Well-posed initial-boundary value problem for the harmonic Einstein equations using energy estimates”, Class. Quantum Grav., 24, 5973–5984, (2007). [DOI], [ADS]. 5.3
Kreiss, H.-O., Reula, O., Sarbach, O., and Winicour, J., “Boundary conditions for coupled quasilinear wave equations with application to isolated systems”, arXiv e-print, (2008). [arXiv:0807.3207]. 5.3
Kreiss, H.-O., and Winicour, J., “Problems which are well posed in a generalized sense with applications to the Einstein equations”, Class. Quantum Grav., 23, S405–S420, (2006). [DOI], [ADS]. 1, 5.3, 5.3
Lehner, L., “A Dissipative Algorithm for Wave-like Equations in the Characteristic Formulation”, J. Comput. Phys., 149, 59–74, (1999). [DOI], [ADS]. 4.2.1, 4.2.2, 4.2.4
Lehner, L., “Matching characteristic codes: exploiting two directions”, Int. J. Mod. Phys. D, 9(4), 459–473, (2000). [DOI], [ADS]. 4.5, 5.5.3
Lehner, L., Bishop, N.T., Gómez, R., Szilágyi, B., and Winicour, J., “Exact solutions for the intrinsic geometry of black hole coalescence”, Phys. Rev. D, 60, (044005), 1–10, (1999). [DOI], [ADS]. 2, 4.3, 4.3
Lehner, L., Gómez, R., Husa, S., Szilágyi, B., Bishop, N.T., and Winicour, J., “Bagels Form When Black Holes Collide”, institutional homepage, Pittsburgh Supercomputing Center. URL (cited on 30 July 2005): http://www.psc.edu/research/graphics/gallery/winicour.html. 4.3
Lehner, L., and Moreschi, O.M., “Dealing with delicate issues in waveform calculations”, Phys. Rev. D, 76, (124040), 1–12, (2007). [DOI], [ADS]. 6, 6
Lindman, E.L., “‘Free-space’ boundary conditions for the time dependent wave equation”, J. Comput. Phys., 18, 66–78, (1975). [DOI], [ADS]. 5.1, 5.1
Linke, F., Font, J.A., Janka, H.-T., Müller, E., and Papadopoulos, P., “Spherical collapse of supermassive stars: Neutrino emission and gamma-ray bursts”, Astron. Astrophys., 376, 568–579, (2001). [DOI], [ADS]. 7.1
Lousto, C.O., and Price, R.H., “Understanding initial data for black hole collisions”, Phys. Rev. D, 56, 6439–6457, (1997). [DOI], [ADS]. 5.4
Marsa, R.L., and Choptuik, M.W., “Black-hole-scalar-field interactions in spherical symmetry”, Phys. Rev. D, 54, 4929–4943, (1996). [DOI], [ADS]. 3.1, 5.5.3
Matzner, R.A., Seidel, E., Shapiro, S.L., Smarr, L.L., Suen, W.-M., Teukolsky, S.A., and Winicour, J., “Geometry of a Black Hole Collision”, Science, 270, 941–947, (1995). [DOI], [ADS]. 2
May, M.M., and White, R.H., “Hydrodynamic Calculations of General-Relativistic Collapse”, Phys. Rev., 141, 1232–1241, (1966). [DOI], [ADS]. 7.1
Miller, J.C., and Motta, S., “Computations of spherical gravitational collapse using null slicing”, Class. Quantum Grav., 6, 185–193, (1989). [DOI], [ADS]. 7.1
Moncrief, V., “Gravitational perturbations of spherically symmetric systems. I The exterior problem”, Ann. Phys. (N.Y.), 88, 323–342, (1974). [DOI], [ADS]. 5.4
Müller Zum Hagen, H., and Seifert, H.-J., “On characteristic initial-value and mixed problems”, Gen. Relativ. Gravit., 8(4), 259–301, (1977). [DOI], [ADS]. 4.3
Nagar, A., and Rezzolla, L., “Gauge-invariant non-spherical metric perturbations of Schwarzschild black-hole spacetime”, Class. Quantum Grav., 22, R167–R192, (2005). [DOI], [ADS]. Corrigendum Class. Quantum Grav., 23, 4297, (2006), DOI:10.1088/0264-9381/23/12/C01. 1, 5.4, 6
Nayfeh, A., Perturbation Methods, (Wiley, New York, 1973). 5.4
Newman, E.T., and Penrose, R., “An Approach to Gravitational Radiation by a Method of Spin Coefficients”, J. Math. Phys., 3, 566–578, (1962). [DOI], [ADS]. Errata: J. Math. Phys., 4, 998, (1963), DOI:10.1063/1.1704025. 2, 5.3
Newman, E.T., and Penrose, R., “Note on the Bondi-Metzner-Sachs Group”, J. Math. Phys., 7, 863, (1966). [DOI], [ADS]. 4.1, 4.1.1
Newman, E.T., and Penrose, R., “New Conservation Laws for Zero Rest-Mass Fields in Asymptotically Flat Space-Time”, Proc. R. Soc. London, Ser. A, 305, 175–204, (1968). [DOI], [ADS]. 3.1
Oren, Y., and Piran, T., “Collapse of charged scalar fields”, Phys. Rev. D, 68, (044013), 1–12, (2003). [DOI], [ADS]. 3.1
Papadopoulos, P., “Nonlinear harmonic generation in finite amplitude black hole oscillations”, Phys. Rev. D, 65, (084016), 1–11, (2002). [DOI], [ADS]. 3.3.2, 4.5
Papadopoulos, P., and Font, J.A., “Relativistic hydrodynamics on spacelike and null surfaces: Formalism and computations of spherically symmetric spacetimes”, Phys. Rev. D, 61, (024015), 1–15, (2000). [DOI], [ADS]. 7.1
Papadopoulos, P., and Font, J.A., “Imprints of accretion on gravitational waves from black holes”, Phys. Rev. D, 63, (044016), 1–5, (2001). [DOI], [ADS]. 7.1
Papadopoulos, P.O., Algorithms for the gravitational characteristic initial value problem, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, 1994). [ADS]. 3.3, 7.2
Penrose, R., “Asymptotic Properties of Fields and Space-Times”, Phys. Rev. Lett., 10, 66–68, (1963). [DOI], [ADS]. 1, 2, 6
Penrose, R., “Gravitational Collapse: The Role of General Relativity”, Riv. Nuovo Cimento, 1, 252–276, (1969). [ADS]. 3.1
Phillips, N.A., “A map projection system suitable for large-scale numerical weather prediction”, in Syono, S., ed., 75th Anniversary Volume, J. Meteorol. Soc. Japan, pp. 262–267, (Meteorological Society of Japan, Tokyo, 1957). 1
Piran, T., “Numerical Codes for Cylindrical General Relativistic Systems”, J. Comput. Phys., 35, 254–283, (1980). [DOI], [ADS]. 5.5.1
Piran, T., Safier, P.N., and Katz, J., “Cylindrical gravitational waves with two degrees of freedom: An exact solution”, Phys. Rev. D, 34(2), 331–332, (1986). [DOI], [ADS]. 5.5.1
Piran, T., Safier, P.N., and Stark, R.F., “General numerical solution of cylindrical gravitational waves”, Phys. Rev. D, 32, 3101–3107, (1985). [DOI], [ADS]. 5.5.1
Poisson, E., and Israel, W., “Internal structure of black holes”, Phys. Rev. D, 41, 1796–1809, (1990). [DOI], [ADS]. 3.1
Pollney, D., Algebraic and numerical techniques in general relativity, Ph.D. Thesis, (University of Southampton, Southampton, 2000). 3.3.4, 5.6
Pretorius, F., “Evolution of Binary Black-Hole Spacetimes”, Phys. Rev. Lett., 95, 121101, (2005). [DOI], [ADS]. 1, 5.3, 6
Pretorius, F., and Israel, W., “Quasi-spherical light cones of the Kerr geometry”, Class. Quantum Grav., 15, 2289–2301, (1998). [DOI], [ADS]. 4.2.7
Pretorius, F., and Lehner, L., “Adaptive mesh refinement for characteristic codes”, J. Comput. Phys., 198, 10–34, (2004). [DOI], [ADS]. 3.1.1, 4.4, 6, 7.3.1
Price, R.H., “Nonspherical Perturbations of Relativistic Gravitational Collapse. I. Scalar and Gravitational Perturbations”, Phys. Rev. D, 5, 2419–2438, (1972). [DOI], [ADS]. 3.1, 4.2.6, 4.4
Price, R.H., and Pullin, J., “Colliding black holes: The close limit”, Phys. Rev. Lett., 72, 3297–3300, (1994). [DOI], [ADS]. 3.1, 4.3
Regge, T., and Wheeler, J.A., “Stability of a Schwarzschild Singularity”, Phys. Rev., 108, 1063–1069, (1957). [DOI], [ADS]. 5.4, 6
Reisswig, C., Bishop, N.T., Lai, C.W., Thornburg, J., and Szilágyi, B., “Characteristic evolutions in numerical relativity using six angular patches”, Class. Quantum Grav., 24, S237–S339, (2007). [DOI], [ADS]. 4, 4.1.2, 4.2.3, 4.2.4, 4.2.5, 6
Renaut, R.A., “Absorbing boundary conditions, difference operators, and stability”, J. Comput. Phys., 102, 236–251, (1992). [DOI], [ADS]. 5.1, 5.1
Rendall, A.D., “Local and Global Existence Theorems for the Einstein Equations”, Living Rev. Relativity, 8, lrr-2005-6, (2000). URL (cited on 03 October 2008): http://www.livingreviews.org/lrr-2005-6. 2
Rezzolla, L., Abrahams, A.M., Matzner, R.A., Rupright, M.E., and Shapiro, S.L., “Cauchy-perturbative matching and outer boundary conditions: Computational studies”, Phys. Rev. D, 59, (064001), 1–17, (1999). [DOI], [ADS]. 1, 5.4
Rinne, O., Lindblom, L., and Scheel, M.A., “Testing outer boundary treatments for the Einstein equations”, Class. Quantum Grav., 24, 4053–4078, (2007). [DOI], [ADS]. 5.3
Ronchi, C., Iacono, R., and Paolucci, P.S., “The ‘Cubed Sphere’: A New Method for the Solution of Partial Differential Equations in Spherical Geometry”, J. Comput. Phys., 124, 93–114, (1996). [DOI]. 4.1, 4.1.2
Ruiz, M., Rinne, O., and Sarbach, O., “Outer boundary conditions for Einstein’s field equations in harmonic coordinates”, Class. Quantum Grav., 24, 6349–6377, (2007). [DOI], [ADS]. 5.3
Rupright, M.E., Abrahams, A.M., and Rezzolla, L., “Cauchy-perturbative matching and outer boundary conditions: Methods and tests”, Phys. Rev. D, 58, (044005), 1–9, (1998). [DOI], [ADS]. 1, 5.4
Ryaben’kii, V., and Tsynkov, S.V., “An application of the difference potentials method to solving external problems in CFD”, in Hafez, M., and Oshima, K., eds., Computational Fluid Dynamics Review 1998, vol. 2, (World Scientific, Singapore; River Edge, 1998). 5.1
Sachs, R.K., “Asymptotic Symmetries in Gravitational Theory”, Phys. Rev., 128, 2851–2864, (1962). [DOI], [ADS]. 3.4
Sachs, R.K., “Gravitational Waves in General Relativity. VIII. Waves in Asymptotically Flat Space-Time”, Proc. R. Soc. London, Ser. A, 270, 103–126, (1962). [DOI], [ADS]. 2, 3.3.4
Sachs, R.K., “On the Characteristic Initial Value Problem in Gravitational Theory”, J. Math. Phys., 3, 908–914, (1962). [DOI], [ADS]. 2, 4.3
Sarbach, O., “Absorbing boundary conditions for Einstein’s field equations”, J. Phys.: Conf. Ser., 91, 012005, (2007). [DOI], [ADS]. 1, 5.3
Scheel, M.A., Shapiro, S.L., and Teukolsky, S.A., “Collapse to black holes in Brans-Dicke theory. I. Horizon boundary conditions for dynamical spacetimes”, Phys. Rev. D, 51(8), 4208–4235, (1995). [DOI], [ADS]. 5.5.3
Scheel, M.A., Shapiro, S.L., and Teukolsky, S.A., “Collapse to black holes in Brans-Dicke theory. II. Comparison with general relativity”, Phys. Rev. D, 51, 4236–4249, (1995). [DOI], [ADS]. 5.5.3
Seidel, E., and Suen, W.-M., “Dynamical evolution of boson stars: Perturbing the ground state”, Phys. Rev. D, 42, 384–403, (1990). [DOI], [ADS]. 3.1, 4.6
Shapiro, S.L., Teukolsky, S.A., and Winicour, J., “Toroidal Black Holes and Topological Censorship”, Phys. Rev. D, 52, 6982–6987, (1995). [DOI], [ADS]. 2, 4.3
Shibata, M., and Nakamura, T., “Evolution of three-dimensional gravitational waves: Harmonic slicing case”, Phys. Rev. D, 52, 5428–5444, (1995). [DOI], [ADS]. 1
Siebel, F., Simulation of axisymmetric flows in the characteristic formulation of general relativity, Ph.D. Thesis, (Technische Universität München, München, 2002). Related online version (cited on 14 April 2009): http://tumb1.biblio.tu-muenchen.de/publ/diss/ph/2002/siebel.html. 1,7.2
Siebel, F., Font, J.A., Müller, E., and Papadopoulos, P., “Simulating the dynamics of relativistic stars via a light-cone approach”, Phys. Rev. D, 65, (064038), 1–15, (2002). [DOI], [ADS]. 4.2.2, 7.2
Siebel, F., Font, J.A., Müller, E., and Papadopoulos, P., “Axisymmetric core collapse simulations using characteristic numerical relativity”, Phys. Rev. D, 67, (124018), 1–16, (2003). [DOI], [ADS]. 7.2, 7.3.1
Siebel, F., Font, J.A., and Papadopoulos, P., “Scalar field induced oscillations of relativistic stars and gravitational collapse”, Phys. Rev. D, 65, (024021), 1–10, (2001). [DOI], [ADS]. 7.1
Sjödin, K.R.P., Sperhake, U., and Vickers, J.A., “Dynamic cosmic strings. I”, Phys. Rev. D, 63, (024011), 1–14, (2001). [DOI], [ADS]. 3.1
Sod, G.A., Numerical Methods in Fluid Dynamics: Initial and Initial Boundary-Value Problems, (Cambridge University Press, Cambridge; New York, 1985). 5.1
Sorkin, E., and Piran, T., “Effects of pair creation on charged gravitational collapse”, Phys. Rev. D, 63, (084006), 1–12, (2001). [DOI], [ADS]. 3.1
Sorkin, R.D., “A Criterion for the Onset of Instability at a Turning Point”, Astrophys. J., 249, 254–257, (1981). [DOI], [ADS]. 3.1
Sperhake, U., Sjödin, K.R.P., and Vickers, J.A., “Dynamic cosmic strings. II. Numerical evolution of excited strings”, Phys. Rev. D, 63, (024012), 1–15, (2001). [DOI], [ADS]. 3.1
Stark, R.F., and Piran, T., “A general relativistic code for rotating axisymmetric configurations and gravitational radiation: Numerical methods and tests”, Comput. Phys. Rep., 5, 221–264, (1987). [DOI]. 5.6
Stewart, J.M., “Numerical relativity”, in Bonnor, W.B., Islam, J.N., and MacCallum, M.A.H., eds., Classical General Relativity, Proceedings of the Conference on Classical (Non-Quantum) General Relativity, City University, London, 21–22 December 1983, pp. 231–262, (Cambridge University Press, Cambridge; New York, 1984). [ADS]. 3.1
Stewart, J.M., “The characteristic initial value problem in general relativity”, in Winkler, K.-H.A., and Norman, M.L., eds., Astrophysical Radiation Hydrodynamics, Proceedings of the NATO Advanced Research Workshop on Astrophysical Radiation Hydrodynamics, Garching, Germany, August 2–13, 1982, NATO ASI Series. Series C, vol. 188, p. 531, (Reidel, Dordrecht; Boston, 1986). [ADS]. 2
Stewart, J.M., “Numerical Relativity III. The Bondi Mass Revisited”, Proc. R. Soc. London, Ser. A, 424, 211–222, (1989). [DOI], [ADS]. 3.3.1, 3.4
Stewart, J.M., “The Cauchy problem and the initial boundary value problem in numerical relativity”, Class. Quantum Grav., 15, 2865–2889, (1998). [DOI], [ADS]. 5.3
Stewart, J.M., and Friedrich, H., “Numerical Relativity. I. The Characteristic Initial Value Problem”, Proc. R. Soc. London, Ser. A, 384, 427–454, (1982). [DOI], [ADS]. 1, 3.3.1
Szilágyi, B., Cauchy-characteristic matching in general relativity, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, 2000). [ADS]. 5
Szilágyi, B., Gómez, R., Bishop, N.T., and Winicour, J., “Cauchy boundaries in linearized gravitational theory”, Phys. Rev. D, 62, (104006), 1–10, (2000). [DOI], [ADS]. 5
Szilágyi, B., and Winicour, J., “Well-posed initial-boundary evolution in general relativity”, Phys. Rev. D, 68, (041501), 1–5, (2003). [DOI], [ADS]. 1, 5.2, 5.3, 5.3, 5.8
Tamburino, L.A., and Winicour, J., “Gravitational Fields in Finite and Conformal Bondi Frames”, Phys. Rev., 150, 1039–1053, (1966). [DOI], [ADS]. 2, 3.4, 6, 7.1
Teukolsky, S.A., “Perturbations of a Rotating Black Hole. I. Fundamental Equations for Gravitational, Electromagnetic, and Neutrino-Field Perturbations”, Astrophys. J., 185, 635–647, (1973). [DOI], [ADS]. 4.4
Teukolsky, S.A., “Linearized quadrupole waves in general relativity and the motion of test particles”, Phys. Rev. D, 26, 745–750, (1982). [DOI], [ADS]. 3.3
Thompson, K.W., “Time dependent boundary conditions for hyperbolic systems”, J. Comput. Phys., 68, 1–24, (1987). [DOI], [ADS]. 5.1
Thornburg, J., “Black-hole excision with multiple grid patches”, Class. Quantum Grav., 21, 3665–3691, (2004). [DOI], [ADS]. 4.1, 4.2.3
Thornburg, J., “A fast apparent horizon finder for three-dimensional Cartesian grids in numerical relativity”, Class. Quantum Grav., 21, 743–766, (2004). [DOI], [ADS]. 4.1, 4.2.3
Ting, L., and Miksis, M.J., “Exact boundary conditions for scattering problems”, J. Acoust. Soc. Am., 80, 1825–1827, (1986). [DOI], [ADS]. 5.1
Trefethen, L.N., and Halpern, L., “Well-Posedness of One-Way Wave Equations and Absorbing Boundary Conditions”, Math. Comput., 47, 421–435, (1986). 5.1
Tsynkov, S.V., Artificial Boundary Conditions Based on the Difference Potentials Method, NASA Technical Memorandum, 110265, (NASA Langley Research Center, Hampton, 1996). Related online version (cited on 04 February 2009): http://hdl.handle.net/2060/19960045440. 5.1
Wald, R.M., General Relativity, (University of Chicago Press, Chicago, 1984). 5.5.3
Weber, J., and Wheeler, J.A., “Reality of the Cylindrical Gravitational Waves of Einstein and Rosen”, Rev. Mod. Phys., 29, 509–515, (1957). [DOI]. 3.1, 5.5.1
Winicour, J., “Newtonian gravity on the null cone”, J. Math. Phys., 24, 1193–1198, (1983). [DOI], [ADS]. 4.2
Winicour, J., “Null infinity from a quasi-Newtonian view”, J. Math. Phys., 25, 2506–2514, (1984). [DOI], [ADS]. 1
Winicour, J., “The quadrupole radiation formula”, Gen. Relativ. Gravit., 19, 281–287, (1987). [DOI], [ADS]. 5.4
Winicour, J., “The Characteristic Treatment of Black Holes”, Prog. Theor. Phys. Suppl., 136, 57–71, (1999). [ADS]. 4.3, 4.3
Xanthopoulos, B.C., “Cylindrical waves and cosmic strings of Petrov type D”, Phys. Rev. D, 34(12), 3608–3616, (1986). [DOI], [ADS]. 3.1
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24–August 4, 1978, pp. 83–126, (Cambridge University Press, Cambridge; New York, 1979). [ADS]. 1
Zerilli, F.J., “Gravitational Field of a Particle Falling in a Schwarzschild Geometry Analyzed in Tensor Harmonics”, Phys. Rev. D, 2, 2141–2160, (1970). [DOI], [ADS]. 5.4, 6
Zlochower, Y., Waveforms from colliding black holes, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, 2002). [ADS]. 1, 4.2.5, 4.4, 4.5, 4.5, 6
Zlochower, Y., Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Mode coupling in the nonlinear response of black holes”, Phys. Rev. D, 68, (084014), 1–16, (2003). [DOI], [ADS]. 1, 3.3.2, 4.2.5, 4.4, 4.5, 4.5, 6
Acknowledgements
This work was supported by National Science Foundation grant PH-0553597 to the University of Pittsburgh. I want to thank the many people who have supplied me with material. Please keep me updated.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Winicour, J. Characteristic Evolution and Matching. Living Rev. Relativ. 12, 3 (2009). https://doi.org/10.12942/lrr-2009-3
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2009-3
Keywords
Article history
Latest
Characteristic Evolution and Matching- Published:
- 25 January 2012
- Accepted:
- 04 January 2012
DOI: https://doi.org/10.12942/lrr-2012-2
- Characteristic Evolution and Matching
- Published:
- 16 April 2009
- Accepted:
- 09 April 2009
DOI: https://doi.org/10.12942/lrr-2009-3
- Characteristic Evolution and Matching
- Published:
- 08 December 2005
- Accepted:
- 19 October 2005
DOI: https://doi.org/10.12942/lrr-2005-10
Original
Characteristic Evolution and Matching- Published:
- 01 December 1998
DOI: https://doi.org/10.12942/lrr-1998-5