1 Introduction

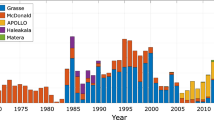
On July 20, 1969, humans landed on the Moon for the first time. The following day, the Apollo 11 astronauts deployed the first Laser Ranging Retroreflector (LRRR or LR3). Within a month, return photons were successfully detected at several observatories [7]. Two more retroreflector arrays were placed on the Moon during the Apollo 14 and 15 missions. In addition, two French arrays were on Russian Lunokhod rovers carried on Luna landers. These five retroreflector arrays remain visible today and the laser ranging data collected over the past 40 years has dramatically and continually increased our understanding of gravitational physics along with Earth and Moon geophysics, geodesy, and dynamics. They remain the only operating lunar experiment from the Apollo era, and more incredibly, only recently has the ground station technology advanced to the point where uncertainties associated with the lunar arrays are limiting the range measurement precision.

The Apollo 11 and 14 arrays consist of 100 fused silica ‘circular opening’ cubes (3.8 cm diameter each) with a total estimated lidar cross section (based on the intensity of the diffraction pattern of the array at the position of the receiver in the far field) of 0.5 billion square meters. Apollo 15 has 300 of these cubes and therefore about 3 times the lidar cross section and is the lunar array with the highest response. The diffraction pattern of the Apollo arrays has a bright central lobe at the center with six surrounding lobes with an effective tophat function 8 arcsec in diameter for small incidence angles [3, 40]. They produce an approximately 20 km diameter spot on Earth [24]. This spread is sufficient to cover the velocity aberration due to the Moon’s motion, so the cube’s reflective face angles were not intentionally spoiled (made different from 90 degrees).

Figure 1
figure 1

From left to right, the Apollo 11, 14, and 15 retroreflector arrays. (Image credits: NASA.)

Full size image

The two Lunokhod arrays consist of 14 triangular shaped cubes, each side 11 cm. Shortly after landing, the Lunokhod 1 array ceased to be a viable target. However, in March 2010, it was located by NASA’s Lunar Reconnaissance Observer. Lunokhod 1 has now become a strong target for laser ranging, contrary to Lunokhod 2, which is very difficult to get returns from during the lunar day [44]. The silver rear coating and larger size of the Lunokhod cubes makes them less thermally stable, which dramatically reduces the optical performance when sunlit.

Lunar laser ranging (LLR) is performed by measuring the round-trip light travel time between a ground transmitter and the retroreflector. Early LLR measurements had a precision of about 20 cm. Since 1969, multiple stations have successfully ranged to the lunar retroreflectors. However, two stations have dominated LLR data generation: McDonald Laser Ranging System (MLRS) in Texas (since 1969) [65] and Observatoire de la Côte d’Azur (OCA) in Grasse, France (since 1985) [59]. The vast majority of their lunar data comes from the array with the highest lidar cross section: Apollo 15. These stations have increased the range precision by a factor of 10 over the years to the level of about two centimeters. Recently, the Apache Point Observatory Lunar Laser-ranging Operation (APOLLO) has begun contributing high-quality data at the millimeter level [6, 42, 43].

Figure 2
figure 2

The Russian Lunokhod 1 lander with the French built retroreflector array sticking out the left side. (Image credits: Lavochkin Association / NASA.)

Full size image

Poor detection rates are a major limiting factor in past LLR. Taking into account velocity aberrations, optical performance of the ground station, and other systematic effects, the overall round-trip loss is typically of order 10−21, mostly due to the r4 loss from the Earth-Moon distance. Because of this heavy loss of light, not every laser pulse sent to the Moon results in a detected return photon, leading to poor measurement statistics. MLRS typically collects less than 100 photons per range measurement with a scatter of about 2 cm. However, the new APOLLO instrument at Apache Point has overcome this limitation.

The large collecting area of the Apache Point 3.5 m diameter telescope and the efficient avalanche photodiode arrays used in APOLLO result in thousands of detections (even multiple detections per pulse) leading to a statistical uncertainty of about 1 mm. The dominant random uncertainty per photon in APOLLO stems from the orientation of the reflector array and the associated spread of pulse return times [6]. Additionally, systematic errors associated with lunar arrays, such as regolith motion and thermal expansion of the array, start to become significant at the millimeter level of precision.

Each ground station records the single-photon reflection events, which are then combined into ‘normal points’ that are adjusted for station-specific corrections. A typical normal point is generated from 5 to 20 minutes of ranging. The normal points are then submitted to a central archive with the International Laser Ranging Service [58], which makes them available to the public. Auxiliary measurements, such as environmental conditions (temperature, pressure, etc.) are also recorded, as these are required to further correct the data for atmospheric effects. A detailed model of the solar system ephemeris is then used to perform a least-squares analysis to estimate various model parameters from the measured data [80].

Arguably, the most fruitful analysis of LLR data is for tests of General Relativity (GR). Relativistic effects typically show up at particular frequencies (such as the synodic frequency) making them separable from most other parameters. These frequency signatures make the analysis possible given the plethora of other effects with large uncertainties. In the following sections, we summarize the main tests of GR performed with LLR. These include tests of the Equivalence Principle, the variation of the gravitational constant, the inverse square law, and a preferred-frame. We then discuss the current state of LLR data analysis. Finally, we describe the next generation of lunar laser ranging instruments and discuss the possibilities that the future of lunar and planetary laser ranging may hold.

Figure 3
figure 3

Improvements in the ground station technology over the past 40 years have increased the range precision by 2 orders of magnitude. Uncertainties associated with the existing retroreflectors are now becoming a limitation. (Image credits: Thomas Murphy.)

Full size image

2 Equivalence Principle

The gravitational acceleration of massive bodies toward other bodies is dependent on the nonlinear properties of gravity within metric theories of gravity [48]. Tracking this acceleration provides a measurement of how gravity pulls on the gravitational binding energy and how gravitational binding energy affects inertia. This probe of nonlinear gravity is explicitly singled out in measurements of the Parameterized Post-Newtonian parameter β discussed below, but it is also implicitly contained within the Einstein Equivalence Principle.

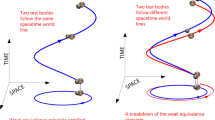
The Equivalence Principle (EP), which states the equality of gravitational and inertial mass, is central to the theory of GR. The EP comes in two flavors: the weak (WEP) and the strong (SEP). The WEP pertains to nongravitational contributions to mass: namely, Standard Model contributions of nuclear and electromagnetic energy, gluons, plus quark masses and their kinetic energies. Nucleons of differing fractional electro-weak and nuclear binding energies might exhibit different couplings to gravity in the case of a WEP violation. The SEP extends the WEP to include gravitational self-energy of a body, addressing the question of how gravity pulls on itself and, therefore, accessing the nonlinear aspect of gravity.

While the EP must hold true in GR, nearly all alternative theories of gravity predict a violation of the EP at some level. Efforts to formulate a quantum description of gravity generally introduce new scalar or vector fields that violate the EP [13, 14]. These violations manifest themselves in the equations of motion for massive self-gravitating bodies, as well as preferred frame and preferred-location effects on the gravitational constant. GR may be the only metric theory of gravity that is dependent on the SEP holding true [72], distinguishing it from all other theories of gravity. Therefore, probing the validity of the EP is one of the strongest ways of testing GR. This test is often considered one of the most powerful ways to search for new physics beyond the standard model [12].

Precision tests of the EP generally test the Universality of Free Fall (UFF): all test bodies have the same gravitational acceleration in a uniform gravitational field. Tests of the UFF are performed by comparing the gravitational accelerations a1 and a2 of different test bodies:

$$\frac{{\Delta a}}{a} = \frac{{{a_1} - {a_2}}}{{\tfrac{1}{2}({a_1} + {a_2})}} = {\left( {\frac{{{M_G}}}{{{M_I}}}} \right)_1} - {\left( {\frac{{{M_G}}}{{{M_I}}}} \right)_2},$$
(1)

where MG is the gravitational mass and MI is the inertial mass of each test body. Laboratory masses lack measurable gravitational self-energy, so the classical Eötvös type experiments, which compare the acceleration of test bodies with different compositions only probe the WEP [60].

In the late 1960s, Nordtvedt recognized that the SEP could be tested by comparing the gravitational acceleration of two massive bodies [48, 47]. For each body, the gravitational to inertial mass ratio can be written as:

$${{{M_G}} \over {{M_I}}} = 1 + \eta {U \over {M{c^2}}},$$
(2)

where U is the gravitational self-energy of the test body:

$$U = {G \over 2}\int {{{\rho (r)\rho (r^{\prime})} \over {\vert r - r^{\prime}\vert}}} {d^3}{\bf{r}}{d^3}{\bf{r}}^{\prime},$$
(3)

Mc2 is the body’s total mass energy, and η is a dimensionless constant that is identically zero if the EP holds true.

For a uniform sphere of radius R, U/Mc2 = −3 GM/5 Rc2. However, due to their complex interior structure, the gravitational self-energy for astronomical bodies is generally computed numerically. An Earth model based on the model described in [25] yields a self-energy of [78]:

$${\left({{U \over {M{c^2}}}} \right)_{{\rm{Earth}}}} = - 4.64 \times {10^{- 10}},$$
(4)

while a Moon with a 20% iron core yields [75]:

$${\left({{U \over {M{c^2}}}} \right)_{{\rm{Moon}}}} = - 1.90 \times {10^{- 11}}.$$
(5)

Nordtvedt realized that a violation of the EP would cause the Earth and Moon to fall at different rates toward the Sun resulting in a polarization of the lunar orbit [49]. This polarization shows up in LLR as a displacement along the Earth-Sun line with a 29.53 day synodic period. Detailed solutions to the equations of motion for the Earth-Moon-Sun system [54, 15] find that the radial perturbation of the Earth-Moon distance due to an EP violation is

$$\delta r = - 2.9427 \times {10^{10}}\left[ {{{\left({{{{M_G}} \over {{M_I}}}} \right)}_{{\rm{Earth}}}} - {{\left({{{{M_G}} \over {{M_I}}}} \right)}_{{\rm{Moon}}}}} \right]\cos \;D\;\;[{\rm{m}}],$$
(6)

where D is the angle between the mean longitude of the Moon and the mean longitude of the Sun as observed from the Earth (synodic period). Combining Equation (2) with the estimated self-energy for the Earth and Moon, we find that Equation (6) becomes:

$$\delta r = 13.1\eta \cos \;D\;\;[{\rm{m}}].$$
(7)

Recent solutions using LLR data yield an EP test numerically comparable with present laboratory limits, at a part in 1013 [79, 60]. Since the Earth and Moon not only have different gravitational self-energy, but also have different compositions the LLR measurements alone do not provide a pure test of SEP [52]. To separate the WEP and SEP effects and eliminate the possibility of a conspiratorial cancellation, the Eöt-Wash group at the University of Washington performed a torsion balance experiment using test masses of similar composition to the Earth and Moon [4]. Combining the torsion balance results with the latest LLR analyses produced the best test of the SEP to date [79, 80]:

$$\Delta {\left({{{{M_G}} \over {{M_I}}}} \right)_{{\rm{SEP}}}} = (- 2.0 \pm 2.0) \times {10^{- 13}},$$
(8)
$$\eta = (4.4 \pm 4.5) \times {10^{- 4}}.$$
(9)

Because Earth’s self-energy contributes 4.5 × 10−10 of its total mass, this translates to a SEP test of 0.04%.

3 Variation of the Strength of Gravity

In GR the coupling strength of gravity is taken as a constant: G. However, not all theories require such a constraint. Within scalar-tensor theories the gravitational coupling can become a function of a dynamical scalar field. The variation of the gravitational constant then depends on the cosmological evolution of the scalar field. The exact form of the variation will depend on the specific cosmological scenario being proposed [71, 27, 46]. It has also been shown that dark energy is compatible with a wide range of models derived from the compactification of higher-dimensional theories if the gravitational constant varies with time [68].

A time variation of G will show up as an anomalous evolution of the orbital periods of astronomical bodies. This is easily seen from Kepler’s third law:

$${P^2} = {{4{\pi ^2}{r^3}} \over {Gm}}.$$
(10)

Taking the time derivative and rearranging we find:

$${{\dot G} \over G} = 3{{\dot r} \over r} - 2{{\dot P} \over P} - {{\dot m} \over m}.$$
(11)

for solar system bodies, we can safely ignore the mass term, except for a small rate of mass loss by the Sun (for compact objects like neutron stars this term becomes important [53]). Both tidalfriction and a changing G influence the semimajor axis. However, one can separate the effects by taking into account their different proportional contributions to the orbital period.

This evolving range, linear with time, was used for analysis of the initial years of LLR data. However, a changing G affects both the monthly lunar orbit and the annual Earth-Moon orbit around the Sun. Solar perturbations on the lunar orbit are also large. Secular change in the annual orbital period from a varying G accumulates as an orbital longitude perturbation evolving quadratically with time [55]. This t2 effect on the phase of the solar perturbations provides a strong limit when measured over decades.

Recent analysis of LLR data by the JPL group sets a limit on Ġ/G = (6 ± 7) × 10−13 year [69]. Similarly, Müller et al. find Ġ/G = (2 ± 7) ± 10−13 year and \(\ddot G/G = (4 \pm 5) \times {10^{- 15}}{\rm{yea}}{{\rm{r}}^2}\) [35]. These limits translate to less than a 1% variation of G over the 13.7 billion year age of the universe. Because the dominant effect for a variation in G is quadratic in time, continued LLR measurements will significantly improve this limit. Additionally, a more optimal measurement schedule throughout the lunar month, now possible with APOLLO, will also put better constraints on a possible time variation of G [56].

4 Inverse Square Law

The inverse square law (ISL) of gravity has been meaningfully tested over length scales spanning 20 orders of magnitude, eliminating Yukawa-like couplings competitive with the strength of gravity from 10−4 to 10−16 meter length scales. The deepest probe of the ISL is from LLR at a scale of ∼ 108 meters, where any new force must be weaker than gravity by more than ten orders-of-magnitude [38]. Short-range tests of the ISL have recently been prompted by the energy scale of the cosmological acceleration, which suggest new-physics below 1 mm [1].

Modern tests of Newton’s inverse-square law of gravity often search for an additional Yukawa contribution to the gravitational potential:

$$V(r) = - G{{{m_1}{m_2}} \over r}\left({1 + \alpha {e^{- r/\lambda}}} \right),$$
(12)

where α is the dimensionless strength and λ is the length scale. Such a potential would generate a precession of the Moon’s perigee with frequency δω [1]:

$${{\delta \omega} \over \omega} = {\alpha \over 2}{\left({{a \over \lambda}} \right)^2}{e^{- a/\lambda}},$$
(13)

where a is the mean radius of the Moon’s orbit. The agreement of geodetic precession with GR described below leads to a limit on an anomalous precession of δω/ω < 1.6 × 10−11. This translates into a limit on the strength of a new Yukawa potential of α < 5.9 × 10−11 at λ = a/2 where the lunar test is most sensitive.

Recent analysis of LLR data includes specifically fitting for Yukawa perturbation terms in the equations of motion leading to a measurement of a = (3 ± 2) × 10−11 at λ = 4 × 105 km. While intriguing, this possible non-null result has yet to be thoroughly investigated [38].

5 The Nature of Spacetime

The recent and unexpected measurement of the accelerating expansion of the universe has provided new motivation for exploring the nature of spacetime. Models that predict modification of gravity at large distances, such as brane-world models, have recently become of interest [18]. These theories exhibit a strong coupling phenomenon that makes the gravitational force source-dependent. These theories become testable at shorter distances, where the coupling sets in for lighter sources [19]. The Earth-Moon system provides a testbed for investigating the nature of spacetime at solarsystem scales. For example, GR predicts that a gyroscope moving through curved spacetime will precess with respect to a rest frame. This is referred to as geodetic or de Sitter precession. The Earth-Moon system behaves as a gyroscope with a predicted geodetic precession of 19.2 msec/year. This is observed using LLR by measuring the lunar perigee precession [8]. The current limit on the deviation of the geodetic procession from the GR prediction is: Kgp = (1.9 ± 6.4) × 10−3 [79]. This measurement can also be used to set a limit on a possible cosmological constant: Λ < 10−26 km−2 [61], which has implications for our understanding of dark energy.

It is also useful to look at violations of GR in the context of metric theories of gravity. Parameterized Post-Newtonian (PPN) formalism provides a convenient way to describe a class of deviations from GR [50]. The most often considered PPN parameters are γ and β: γ indicates how much space curvature is produced per unit mass, while β indicates how nonlinear gravity is (self-interaction). γ and β are identically one in GR. Also of interest are the preferred-frame parameters α1 and α2, which are identically zero in GR [73, 57].

Limits on γ can be set from geodetic precession measurements [50], but the best limits presently come from measurements of the gravitational time delay of light, i.e., the Shapiro effect [62]. Doppler measurements to the Cassini spacecraft set the current limit on γ: (γ − 1) = (2.1 ± 2.3) × 10−5 [9].

The Equivalence Principle parameter η depends on the PPN parameters β and γ:

$$\eta = 4\beta - \gamma - 3.$$
(14)

Combining the Cassini value for γ with the LLR value for η provides the best limit on β: (β − 1) = (1.2 ± 1.1) × 10−4 [79]. Scalar tensor theories with’ attractors’ for the cosmic background scalar-field dynamics predict a residual γ − 1 and perhaps β − 1 of order 10−7 -10−5 today [14], within reach of advanced LLR and spacecraft time-delay measurements.

A nonzero preferred frame would show up as an oscillation of the lunar range at the sum and the difference of the anomalistic frequency and the annual period [16, 37]. Recent analysis of LLR data sets the current limit on the PPN parameter α1 = (−7 ± 9) × 10−5 [38]. LLR has also been used to set a limit on α2 = (1.8 ± 2.5) × 10−5 [38]. However, the close solar spin axis alignment with the total solar system angular momentum produces a much tighter constraint on α2 of order 10−7 [51].

Lunar laser ranging also places limits on the gravitomagnetic interaction, the same physical interaction that leads to the Lense-Thirring and Schiff precession phenomena as tested by precession of the Laser Geodynamics Satellites (LAGEOS) orbital plane and by the precession of a gyroscope in Gravity Probe B respectively [41]. In the case of the lunar orbit, rotation is not involved, but rather translation of the Earth and Moon point-masses in the solar system barycenter frame that produce 6 meter amplitude range signatures at both the synodic frequency and twice the synodic frequency. The amplitudes of these signatures are frame-dependent, reflecting the deep connection gravitomagnetism has with the covariant property of relativistic dynamics. Soffel et al. showed the need for the gravitomagnetic term in the LLR equations of motion at the level of 0.15%, whether confined to a PPN context or allowed to vary independently [67]. If another experiment claimed a gravitomagnetic, or “frame-dragging” departure from GR at even the 1% level, LLR data would stand in conflict [39].

6 Modeling and Analysis

The analysis of LLR data requires a sophisticated model of the solar system ephemeris that also includes all the significant effects that contribute to the range between the Earth stations and the lunar retroreflectors. These models compute a range prediction and the partial derivatives of range with respect to each model parameter at the epoch of each normal point. The model predictions take into account orbital parameters, attraction to the Sun and planets, relativistic corrections, as well as tidal distortions, plate motion, and other phenomena that affect the position of the retroreflector and ground station relative to the centers of mass of the Earth and Moon [80]. Some of these parameters are measured by other means, but most are estimated from the LLR data. The range measurements are corrected for atmospheric delay and a weighted least square analysis is performed to estimate the ∼ 170 parameters in the model [38, 36], most of which are initial conditions and masses of solar system bodies. LLR data is often combined with other spacecraft and planetary tracking data to further constrain the estimates or remove degeneracies.

A number of models have been developed over the past 40 years. The model developed at the Jet Propulsion Laboratory (JPL) was one of the first programs for LLR analysis [83] and continues to be updated. It was recently used to produce limits on the SEP violation, time variation of the gravitational constant, and interior structure of the Moon [80, 81]. The open-source Planetary Ephemeris Program (PEP) is undergoing a major upgrade for LLR analysis at the Harvard-Smithsonian Center for Astrophysics (CfA). It was also used for one of the first LLR analyses to test the SEP [63] and was recently used to test for Lorentz violation using LLR data [5]. A model developed at the University of Hannover was also recently used to produce limits on the relativity parameters, including the preferred frame PPN parameters [36, 38].

With the now routine operation of APOLLO at Apache Point, millimeter level data is being produced [6]. Unfortunately, none of the ephemeris models is currently capable of handling millimeter class data to maximum advantage [82]. New effects and error reduction techniques that become important at the millimeter level need to be added to the analysis tools. To take advantage of the next generation of LLR instruments, these codes will need to be further modified and rigorous theoretical work will need to be performed to permit tests of new ideas in physics. Substantial effort is also required to address the multitude of effects that will contribute at that level.

Many of these effects will be scientifically interesting in their own right. In particular, the lunar interior models require significant improvement. There are also additional Earth effects that need further model development, such as the loading of the lithosphere by the atmosphere and ocean, which causes the observing station to move vertically (and horizontally) with the tides and weather. Models of these effects are available that are deemed accurate to better than 0.1 mm and tested in VLBI analysis software at CfA [64], but need to be incorporated into the analysis programs. As ranging precision is further improved, more sophisticated atmospheric models and auxiliary measurements will need to be developed. Other important effects for advanced LLR analysis include solar radiation pressure, thermal cycling of the reflectors, solar tides on the moon, and solar mass changes [82].

7 Next Generation Lunar Laser Ranging

The lunar retroreflectors used in past analysis (excluding Lunokhod 1 as it was only recently rediscovered) all lie within 26 degrees latitude of the lunar equator, and the most useful ones within 24 degrees longitude of the sub-Earth meridian [77, 17] as shown in Figure 4 and Table 1. This clustering is sub-optimal, particularly with respect to measuring the lunar librations. In addition, the active LLR ground stations do not cover a large range of latitudes, further weakening the geometric strength of the observations. Additional observatories could improve the situation somewhat, but Mt. Stromlo in Australia is the only station capable of ranging to the Moon not situated at similar northern latitudes. Unfortunately, Mt. Stromlo has not been active in ranging to the Moon.

Figure 4
figure 4

Location of the lunar retroreflector arrays. The three Apollo arrays are labeled AP and the two Luna arrays are labeled LUN. ORI and SHK show the potential location of two additional sites that would aid in strengthening the geometric coverage.

Full size image
Table 1 Location of the lunar retroreflector arrays in the DE421 Principal-Axis Frame and their orientation sensitivity (sine of the offset angle from the line connecting the ranging station to the center of the moon) [44, 74, 17].
Full size table

The frequency and quality of observations also varies greatly with the power of the laser employed and other characteristics of the facility. Most ranging over the recent past has occurred between three ground stations (MLRS, OCA, and Apache Point) and one reflector (Apollo 15). The solar noise background and other issues make ranging to some reflectors possible only around the quarter-moon phase for most stations other than Apache Point, which has very good distribution among the reflectors. APOLLO is capable of ranging during all lunar phases, but it must share time on its 3.5 meter telescope with other programs.

Improvements in the geometric coverage, both on Earth and on the Moon, will have a direct impact on the science gained through LLR. Studies of the structure and composition of the interior require measurements of the lunar librations, while tests of GR require the position of the lunar center of mass. In all, six degrees of freedom are required to constrain the geometry of the Earth-Moon system (in addition to Earth orientation). A single ranging station and reflector is insufficient to accurately determine all six degrees of freedom, even given the rotation of the Earth with respect to the Moon. The addition of one or more reflectors and one or more additional ranging stations in the Earth’s southern hemisphere would strengthen the geometric coverage and increase the sensitivity to lunar motion by as much as a factor of 4 in some degrees of freedom at the same level of ranging precision [34]. The rediscovery of Lunokhod 1 will also greatly improve the geometric coverage, and consequently, the science return.

Satellite Laser Ranging (SLR) began in 1964 at NASA’s Goddard Space Flight Center. Since then it has grown into a global effort, represented by the International Laser Ranging Service (ILRS) [58]. The ILRS includes ranging to Earth-orbiting artificial satellites, ranging to the lunar reflectors, and is actively working toward supporting asynchronous planetary transponder ranging. The current SLR network consists of over 40 stations worldwide, funded and operated by research organizations, universities, and foreign governments (see Figure 5). It varies widely in its designs for tracking mounts, telescopes, receivers, timing electronics, and laser transmitters.

Figure 5
figure 5

Worldwide distribution of satellite laser ranging stations participating in the International Laser Ranging Service [58]. (Image credits: ILRS.)

Full size image

The development of NASA’s Next Generation Satellite Laser Ranging (NGSLR) system has moved system operation from the regime of high laser energy/low repetition rate to high repetition rate single photon detection [21, 33]. This technique uses receive photons more efficiently and because of the higher return rate, minimizes acquisition time and enables closed loop tracking. The current laser in use (300 picosecond pulsewidth) limits single shot measurement accuracy to 2 to 3 cm but, because of the high return rate, normal point data can be reduced to the millimeter level. As many as 12 NGSLR stations are expected to be built and deployed around the world under NASA’s Earth Science Program in the coming decade. The first of these systems is now operational on the 40 cm telescope at NASA’s Goddard Space Flight Center. It is currently ranging to targets at altitudes ranging from Low Earth Orbiting (LEO) satellites to LAGEOS, as well as up-link ranging to the Lunar Reconnaissance Orbiter (LRO) [33].

The development of this new network of SLR stations provides a potential opportunity to expand the number of LLR stations. To be lunar capable, the SLR stations would need to be upgraded with higher power lasers or, alternatively, new high cross section retroreflectors and/or laser transponders would need to be put on the Moon. Taking advantage of the existing SLR infrastructure is a very compelling way to increase both the spatial and temporal LLR coverage at minimal cost, and would ensure continuous availability of LLR data through the indefinite future as it would not rely on unique facilities and individual investigators continuing operations.

8 Next Generation Lunar Retroreflectors

Remarkably, the five lunar retroreflector arrays are still visible and producing useful data after 40 years of exposure to the lunar environment. During that time, the precision of the range measurements has improved each time the ground stations were upgraded to the most advanced ranging technology at the time. This is despite the fact that the efficiency of the arrays appears to have degraded by a factor of 10 [45]. Incredibly, it has taken nearly 40 years for the ground stations to catch up with the potential capability of the retroreflector arrays.

The first LLR measurements had a precision of about 20 cm. Since 1969, several stations have successfully ranged to the lunar retroreflectors and have increased the range accuracy by a factor of 10 to the level of a few centimeters. Poor detection rates have historically limited LLR precision (not every laser pulse sent to the Moon results in a detected return photon). However, the relatively new APOLLO system uses the large collecting area of the Apache Point telescope, a tightly collimated beam, good atmospheric image quality, and has very efficient avalanche photodiode arrays such that thousands of detections are recorded (even multiple detections per pulse) leading to a statistical uncertainty of about 1 mm for timescales of less than 10 minutes [6, 43].

The dominant random uncertainty per photon received by APOLLO stems from the physical size of the arrays and their changing orientation due to the lunar librations. The incoming pulse from APOLLO will illuminate an entire array, but only one (sometimes a few) of the photons will be detected upon return. APOLLO cannot determine what area of the array contributed most of the returned light, so the tilt of the array with respect to the Earth spreads out the distribution of laser pulses. The typical array dimension (Apollo 11 and 14) of 0.5 m and a typical libration angle of 6 degrees translates to a full-width pulse-spread of about 330 ps in the round-trip time. As the Moon librates, the amount of spreading changes since the array is also changing its orientation with respect to the ground station.

Modest improvements in the ranging technology will not significantly improve the range precision as the array tilt will continue to dominate the error budget for the foreseeable future. In addition, new arrays with more (or less) cubes of the same size would result in no gain: doubling the physical dimension doubles the random uncertainty requiring four times as many photons, exactly what doubling the linear array dimension provides. Likewise, the reduction in return photons would eliminate any benefit of going with a smaller array.

To maintain the advantage that multiple cubes provide in response, but eliminate the issues with orientation, one can separate the cubes far enough that their responses do not overlap when seen by the Earth stations. A range separation of about 10 cm between the cubes should be sufficient to distinguish them in the data. Since the typical (for APOLLO) 5 microradian laser beam covers a 2 km spot on the moon, any reasonable spacing will result in illumination of the entire set of reflectors at once. The cubes could be coarsely surveyed individually to provide enough information to be acquired by the lower energy Earth laser stations, or the initial acquisition from the ground could be performed with the higher laser energy / larger telescope lunar laser ranging Earth stations, which will have good signal-to-noise ratios.

Large single cube corners can also be made to provide similar return rates as the Apollo arrays without significant pulse spreading. The response from a 7.6 cm cube would be 16 times larger than that of the Apollo 3.8 cm cubes. However, simply making solid cubes larger increases their weight by the ratio of the diameters cubed. The additional size also adds to thermal distortion effects and decreases the return beam divergence: a very narrow divergence can cause the return spot to completely miss the station due to velocity aberration. Spoiling (making the dihedral angles of the cube different from 90 degrees) can compensate for the velocity aberration but reduces the effective cross section.

Solid cube corner retroreflectors (up to 11 cm) have flown on over a hundred missions, for both satellites and lunar laser ranging. Recent tests of the 10 cm cube shown in Figure 7 has demonstrated it meets relevant requirements for the lunar environment [11]. Designs for the housing are still in development [23].

Figure 6
figure 6

Example data from APOLLO from the Apollo 15 array on November 19, 2007, in which 6624 photons were collected in a 5000 shot run. The raw time events are shown in the top plot (with the initial predicted round trip time subtracted). The bottom plot shows the distribution of the outgoing pulses, which when convoluted with the retroreflector tilt is consistent with the measured returns shown in the central plot. The trapezoidal overplot represents the temporal spread due to the orientation of the retroreflector at the time of the observation [43]. (Image credits: Thomas Murphy.)

Full size image
Figure 7
figure 7

A 10 cm solid cube corner reflector was recently qualified for the lunar environment. Also shown for comparison is a 3.8 cm Apollo engineering model cube corner [11]. (Image credits: Douglas Currie.)

Full size image

The main disadvantage of large solid cubes is that the thermal requirements become very challenging because of the temperature dependence of the cube material’s index of refraction. A promising alternative is to use hollow (open) cube corners. Since hollow cubes are reflective, the index of refraction problem goes away. They also potentially weigh less, have smaller thermal distortions, and do not introduce significant polarization effects. Therefore, they can be made larger without sacrificing as much in optical performance. Hollow cubes have flown on a few missions, but are generally not used on satellites for laser ranging because of a lack of test data and some indications of instabilities at high temperatures. A recent program at NASA Goddard Space Flight Center is looking at applying advanced bonding techniques for space optics that have the potential for mitigating these problems.

Isolation from ground motion and thermal changes are also key for going beyond the Apollo array capabilities. Each reflector should be rigidly grounded to directly sense lunar body motion and be located far enough away from normal human activity to prevent vibration and contamination (dust) from affecting the cubes. To provide thermal stability, the retroreflectors could be thermally coupled to the ground below the surface layer. As shown in Figure 8, measurements from the Apollo 15 and 17 heat flow probes indicate that the large diurnal temperature fluctuations are negligibly small at depths below 0.8 meters [32, 28]. To take advantage of this stability, one could drill a hole about a meter deep and insert a rod with high conductivity and a low coefficient of thermal expansion to stabilize the retroreflector temperature. The retroreflector package would be mounted to the exposed end of the rod. A thermal blanket positioned over the lunar surface around and below the retroreflector would also reduce the thermal fluctuations induced from the surrounding regolith.

Figure 8
figure 8

Temperature fluctuations in the lunar regolith as a function of depth from Apollo 15 and 17 measurements. Hatched areas show day-night temperature fluctuations. Below about 80 cm there was no observable temperature fluctuation due to the lunar day-night temperature cycles [32].

Full size image

9 Laser Transponders

Laser transponders are currently being developed for satellite laser ranging, but they can also be deployed on the lunar surface as an alternative to retroreflectors [20]. Transponders are devices that both send and receive predictable signals and can be used for ranging and time transfer. They have an approximately r2 link advantage over direct ranging loss of 1/r4, as the signal is propagating in only one direction before being received. With the development and inclusion of laser communications for spaceflight missions, it is logical to include an optical transponder that uses the same opto-mechanical infrastructure with minimal impact on the mission resources. These instruments could be used to support the relativistic and lunar science in addition to providing communications support to astronauts and/or other scientific instruments. These lunar instruments would also provide a pathfinder for applications on Mars and other planetary bodies where the use of passive retroreflectors is not practical.

Asynchronous Laser Transponders (ALT) are relatively simple devises that have good potential for space applications. The ground and remote stations of ALT fire their lasers independently (as opposed to an echo transponder, which works by sending back a timing signal with a fixed delay from the receipt of the base-station signal). This allows the use of free-running lasers on the space-based terminal to operate at their most efficient repetition rates. It is also simpler and potentially more reliable than other types of laser transponders. However, it does require a clock on both ends.

Several interplanetary laser transponder experiments were successfully performed from the NASA Goddard Space Flight Center satellite laser ranging facility. The first (two-way, 24 × 106 km link) utilized the Mercury Laser Altimeter on the Messenger spacecraft [66] and the second (oneway, 80 × 106 km link) utilized the Mars Orbiting Laser Altimeter on the Mars Orbiter spacecraft [84]. More recently, two-way ranging was successfully performed using the Lunar Obiter Laser Altimeter (LOLA) on the Lunar Reconnaissance Orbiter (LRO) orbiting the Moon [33]. These experiments have proven the concept of being able to point both transceivers, detect the photons, and retrieve useful parameters at low-link margins over interplanetary distances.

An ALT, shown in Figure 9, is currently under development at NASA Goddard Space Flight Center that uses technology derived from the Next Generation Satellite Laser Ranging (NGSLR) system [22]. Other efforts at Goddard and other institutions are currently underway that combine laser ranging and laser communications. The robust link budget combined with the potential compatibility with NGSLR would open up to the possibility of using a large number of existing ground stations, which would not only increase the scientific potential, but also significantly reduce the ground station and operational costs.

Figure 9
figure 9

An Asynchronous Laser Transponder is under development at NASA Goddard Space Flight Center that is compatible with the Next Generation Satellite Laser Ranging (NGSLR) system [22].

Full size image
Figure 10
figure 10

NASA’s NGSLR system is being used to laser range to the Lunar Reconnaissance Orbiter (LRO) orbiting the moon [33]. (Image credits: Tom Zagwodzki / GSFC.)

Full size image

10 Outlook

In addition to the tests of gravity, new LLR instruments would be of great benefit to studies of the interior structure of the Moon. Tighter constraints resulting from more complete tracking could aid in the search for a solid inner core. The second-degree tidal lunar Love numbers are detected by LLR, as well as their phase shifts. From past measurements, a fluid core of ∼ 20% of the Moon’s radius is indicated. A lunar tidal dissipation of Q = 30 ± 4 has been reported to have a weak dependence on tidal frequency [76]. Evidence for the oblateness of the lunar fluid-core/solid-mantle boundary may be reflected in a century-scale polar wobble frequency. The lunar vertical and horizontal elastic tidal displacement Love numbers h2 and l2 are known to be no better than 25% of their values, and the lunar dissipation factor Q and the gravitational potential tidal Love number k2 no better than 11%. These values have been inverted jointly for structure and density of the core [30, 29], implying a liquid core and regions of partial melt in the lunar mantle.

Lunar interior studies have arguably suffered the most from the clustering of the Apollo arrays on the central portion of the moon. The rediscovery of the Lunokhod 1 array should greatly improve the situation. In addition, placing retroreflectors far from the Apollo arrays, at a pole or a limb, would improve the measurements by up to a factor of 4 at the same level of ranging precision as is currently performed [34].

The advancement of active laser ranging systems also opens up the possibility of precision ranging beyond the Moon. Laser ranging to Mars can be used to measure the gravitational time delay as Mars passes behind the Sun relative to the Earth. With 1 cm precision ranging, the PPN parameter γ can be measured to about 10−6, ten times better than the Cassini result [70]. The Strong Equivalence Principle polarization effect is about 100 times larger for Earth-Mars orbits than for the lunar orbit. With 1 cm precision ranging, the Nordtvedt parameter, η = 4β − γ − 3, can be measured to between 6 × 10−6 and 2 × 10−6 for observations over ten years [2]. Combined with the time delay measurements this leads to a measurement of PPN parameter β to the 10−6 level. Mars ranging can also be used in combination with lunar ranging to get more accurate limits on the time variation of the gravitational constant.

The ephemeris of Mars itself is known to meters in plane, but hundreds of meters out-of-plane [31]. Laser ranging would get an order of magnitude better estimate, significant for interplanetary navigation. Better measurements of Mars’ rotational dynamics could provide estimates of the size of its core [26]. Mars’ elastic tidal Love number is predicted to be less than 10 cm, within reach of laser ranging. There is also an unexplained low value of Q, inferred from the secular decay of Phobos’ orbit that is a constraint to the present thermal state of the Mars interior [10]. Laser ranging to Phobos would help solve this mystery.

LLR remains one of the best tests of gravity in the weak field and promises to continue to be a key tool for many years to come. The five lunar retroreflectors remain visible today and continue to produce valuable data. Advances in ranging technology have finally reached the point where the precision of the data is being limited by the physical characteristics of the lunar arrays. The natural next step in LLR is to place new retroreflectors and/or laser transponders on the Moon at sites far from the Apollo arrays that have a high enough return rate to take advantage of the SLR network of ground stations. With the retroreflectors and transponder technology available today, these new instruments could easily support laser ranging and advances in ground station technology for another productive 40 years of LLR.