Abstract
We review the current status of general relativistic studies for the coalescence of black hole-neutron star (BH-NS) binaries. First, procedures for a solution of BH-NS binaries in quasi-equilibrium circular orbits and the numerical results, such as quasi-equilibrium sequence and mass-shedding limit, of the high-precision computation, are summarized. Then, the current status of numerical-relativity simulations for the merger of BH-NS binaries is described. We summarize our understanding for the merger and/or tidal disruption processes, the criterion for tidal disruption, the properties of the remnant formed after the tidal disruption, gravitational waveform, and gravitational-wave spectrum.
Similar content being viewed by others
1 Introduction
1.1 Overview of BH-NS binaries
Black hole-neutron star (BH-NS) binaries are believed to be formed as a result of two supernovae in a massive binary system (see [125] for an alternative possibility). After their formation, the orbital separation decreases gradually due to the longterm gravitational radiation reaction (i.e., two objects are in an adiabatic inspiral motion), and eventually, two objects merge to be a black hole system. The lifetime of a binary in quasi-circular orbit is approximately written by (see [156, 155] or Chapter 16 of [186])
where r, MBH, and MNS are the orbital separation, masses of the BH and NS, respectively, and m0 = MBH + MNS. G is the gravitational constant and c the speed of light, respectively. The lifetime for a binary of elliptic orbits with the semi-major axis r is shorter than τGw [156, 155]. Thus, if the initial semi-major axis is smaller than ∼ 107 km, the BH and NS merge within the Hubble time scale after a substantial emission of gravitational waves [155]. In most of the inspiral phase during which the binary separation gradually decreases due to the gravitational radiation reaction, two compact objects are well approximated by two point masses in an adiabatic orbit, because their radii are much smaller than the orbital separation (finite-size effects, such as tidal deformation, are negligible) and also the gravitational-radiation-reaction time scale is much longer than the orbital period (cf. Equation (2) with r ≫ Gm0/c2). The evolution through the inspiral phase is well understood within the post-Newtonian (PN) approximation [25]. On the other hand, throughout the late inspiral to the merger phases, the orbital evolution process depends significantly on their finite-size effects and the resulting modification on the interaction between the two objects. In addition, the adiabatic approximation for the orbital evolution becomes worse, because the gravitational-radiation-reaction time scale is as short as the orbital period; the ratio of τGW to the orbital period, Porb, is approximately written as
and thus, for the orbit close to the last one with r ∼ 6 Gm0/c2, τGW is comparable to Porb. In particular, in the merger phase and subsequent remnant-formation phase, the dynamics of the system depends strongly on the structure of the NS (the radius and density profile, or its equation of state; hereafter EOS) and the BH spin, as well as on general relativistic gravity. This implies that a numerical study in the framework of general relativity is required for precisely understanding the final evolution phase of BH-NS binaries.
BH-NS binaries have not been observed yet even in our galaxy in contrast to NS-NS binaries [205, 131]. However, many of statistical studies based on the stellar evolution synthesis suggest that the coalescence will occur by 1–10% as frequently as that of NS-NS binaries in our galaxy and hence in the normal spiral galaxies [144, 160, 223, 98, 97, 20, 21, 148] (every ∼ 106–107 years). In addition, coalescence in elliptic galaxies could contribute to the total coalescence rate of the universe by a significant fraction [147]. This implies that coalescence is likely to occur frequently in the Hubble volume, and therefore, the evolution process and the final fate of BH-NS binaries deserve a detailed theoretical study. In particular, the following two facts have recently enhanced the motivation for the study of BH-NS binaries: First, BH-NS binaries in close orbits are among the most promising sources for the large laser-interferometric gravitational-wave detectors, such as LIGO [126, 2, 1], VIRGO [222, 4, 3], LCGT [120], and Einstein Telescope [91, 92]: The frequency and amplitude of gravitational waves near the last orbit are estimated to give
where μ is the reduced mass of the binary defined by MBHMNS/m0, and D is the distance to the source. The frequency for the late inspiral orbits is just within the frequency-band sensitivity for the advanced gravitational-wave detectors, ∼ 10–3000 kHz, and the amplitude of ∼ 10−22 is high enough that the signal of gravitational waves may be detected. The detection rate of BH-NS binaries will be ∼ 0.5–50 events per year for the advanced detectors such as advanced-LIGO [126]. To detect gravitational waves and to extract physical information from the gravitational-wave signal, theoretical templates must be prepared. This has motivated PN and numerical-relativity studies as well as two-body approximate general relativistic studies (e.g., [37, 50, 11, 12]) for the coalescing compact binaries. The second fact is that BH-NS binaries may be some of the progenitors of the central engine of gamma-ray bursts with short time duration ≲2s (SGRB) [142], for which the source is still unknown. To elucidate whether the merger of BH-NS binaries could be a promising source for the progenitor of the central engine, numerical-relativity simulations are required (see also Section 1.3).
The final fate of BH-NS binaries is classified into two categories; a NS is tidally disrupted by its companion BH before it is swallowed by the BH or a NS is simply swallowed by its companion BH in the final phase. There is a third possibility, in which stable mass transfer occurs after the onset of mass shedding of the NS by the BH tidal field. Although this may be possible, numerical simulations performed so far have not shown this to be the case, as will be mentioned in Section 1.6.
The final fate of a NS depends primarily on the mass of its companion BH and the compactness of the NS. When the BH mass is small enough or the NS radius is large enough, the NS will be tidally disrupted before it is swallowed by the BH. A necessary (not sufficient) condition for this is semi-quantitatively derived from the following analysis. Mass shedding of a non-spinning NS occurs when the tidal force of its companion BH at the surface of the NS is stronger than the self-gravity of the NS. This condition is approximately (assuming Newtonian gravity) written as
where RNS is the circumferential radius of the NS at r → ∞. cr is a function of r and an EOS-dependent parameter, which is larger than unity and denotes a degree of tidal deformation of the NS, i.e., the semi-major axis is assumed to be elongated as cRRNS. The left-hand side denotes the tidal force by the BH at the surface of the NS and the right-hand side is the self-gravitational force of the NS at the inner edge of its surface.
We emphasize here that Equation (5) is the necessary condition for the onset of mass shedding, strictly speaking. Tidal disruption occurs after substantial mass is stripped from the surface of the NS, during the decrease of the orbital separation due to gravitational-wave emission. Thus, tidal disruption should occur for a smaller orbital separation (larger orbital angular velocity) than that derived from Equation (5). We also note that the NS radius is assumed to depend weakly on the NS mass. If the radius quickly increases with mass loss, tidal disruption may occur soon after the onset of mass shedding.
Assuming that the binary is in a circular orbit with the Keplerian angular velocity, Equation (5) may be written in terms of the angular velocity \(\Omega (= \sqrt {G{m_0}/{r^3}})\) as
where Q denotes the mass ratio defined by MBH/MNS. The latest general-relativistic numerical study for quasi-equilibrium states of BH-NS binaries derives a more quantitative result [209, 210] (see Section 2),
where the value of the constant, CΩ, is ≲ 0.3 for a system composed of a NS of irrotational velocity field and a non-spinning BH. The small value of CΩ (\({C_\Omega}(< \sqrt {0.5})\)) indicates that mass shedding is enhanced by significant tidal deformation (i.e., cR > 1) and/or possibly by general relativistic gravity of the NS. Equation (7) indicates that the frequency of gravitational waves at mass shedding is
Thus, tidal disruption is likely to occur for a high frequency f ≳ 1 (0.7) kHz for a NS of MNS = 1.4 M⊙ and RNS = 12 (15) km, irrespective of the BH mass.
Up to now, we implicitly assume that orbits with arbitrary orbital separations may be possible for the binary system. However, BH-NS binaries always have the innermost stable circular orbit (ISCO) determined by the general relativistic effect, and hence, we should impose the condition that mass shedding (and tidal disruption) has to occur before the binary orbit reaches the ISCO in this analysis. According to PN analysis [25], a non-dimensional orbital compactness parameter, Gm0Ω/c3, at the ISCO, is ∼ 0.10 for 1 ≤ Q ≤ 5 for a system composed of a non-spinning BH and a NS. (The tidal-deformation effect reduces this value by ∼ 10–20% [209, 210]). In the presence of the ISCO, the condition for the onset of mass shedding is written by
where ΩISCO is the angular velocity at the ISCO, and \({{\mathcal C}_{{\rm{ISCO}}}} \sim 0.1\) for a system composed of non-spinning BH (for a spinning BH, this could be much larger than 0.1; see Section 1.2). Equation (9) is rewritten to give
where \({\mathcal C}\) denotes the compactness of the NS, which will be, according to nuclear physics theories for high-density matter, in the range between ∼ 0.12 and ∼ 0.25 [115, 116] for the typical NS of mass 1.2–1.5 M⊙. This estimate suggests that tidal disruption by a non-spinning BH could occur for a binary of a relatively low mass ratio of Q ≲ 5. Equation (10) also shows that the conditions for the onset of mass shedding and for tidal disruption depend strongly on the compactness of the NS.
In the above simple estimate, the tidal-deformation effect of the NS to the orbital motion is not taken into account. As a result of the tidal deformation, the gravitational force between two stars is modified, so are the orbital evolution and the criterion for tidal disruption. Lai, Rasio, and Shapiro [111, 113, 112] thoroughly investigated the effects associated with tidal deformation in the Newtonian framework with the ellipsoidal approximation. They found that the two-body attractive force is strengthen by the effect of the tidal deformation and, by this, the orbital separation of the ISCO is increased (see [165, 166, 114, 190] for related issues) and that gravitational waveforms in the late inspiral phase are modified (see [66, 68, 67, 72] for related issues). Uryū and Eriguchi confirmed the fact that the tidal force modifies the orbital motion of BH-NS binaries by numerically computing equilibrium states of a binary composed of a point mass and a fluid star. The essence is that in addition to the Newtonian potential, which has the form ∝ r−1, the correction term of the form ∝ r−6 appears when a NS is tidally deformed. The magnitude of this correction increases steeply with the decrease of the orbital separation, and modifies the location of the ISCO. Also, the tidal effect accelerates the orbital evolution, because the orbital velocity (and the centrifugal force) has to be increased to maintain circular orbits in an enhanced attractive force, and then, the emissivity of gravitational waves is enhanced, leading to a shorter inspiral time.
1.2 Tidal problem around a BH: Effects of BH spin and the NS EOS
As shown by a simple estimate in the previous Section 1.1, the final fate of BH-NS binaries depends primarily on the mass ratio, Q, and the compactness of the NS, \({\mathcal C}\). However, a detailed analysis has shown that the BH spin and the NS EOS also play an important role in determining the final fate. In particular, the effect of the BH spin can be significant.
A general relativistic study for the criterion of mass shedding (note again that this is not the criterion of tidal disruption) was first performed using an analysis of the tidal interaction between a fluid star and a Kerr BH in circular orbit [71, 137, 135, 191, 225, 94, 69, 70, 154]. In this class of analysis, one handles a fluid star orbiting a Kerr BH in a circular orbit (the center of the fluid star has a geodesic motion around the Kerr BH), and analyzes the structure of the star taking into account the tidal field of the Kerr BH located at the center. Specifically, one analyzes the Euler equation in the following form
where τ is the affine parameter of a geodesic around the BH, xi is a coordinate orthogonal to the geodesic, u i denotes the internal velocity of the fluid star, ρ is the rest-mass density, P is the pressure, ϕ is the Newtonian potential, which obeys Δϕ = 4πGρ, and C ij determines the lowest-order tidal field [135]. Higher-order corrections of the tidal potential based on the Manasse-Misner formalism [134] are also given in [94].
The gravitational effect of the fluid star on the orbital motion, the gravitational radiation reaction, and the relativistic effect on the self-gravity of the star are in general neglected (see [69] for a more detailed phenomenological analysis). Thus, this analysis is valid only for the case in which the BH mass is much larger than the NS mass and t the radius of the NS is relatively large: For the case of BH-NS binaries of mass ratio ≲ 10, this analysis can provide only a qualitative or semi-quantitative nature of the tidal effect and orbital evolution. However, by this analysis, several important qualitative properties of the criterion of mass shedding have been found. One of the most important findings is that the criteria for the onset of mass shedding (and/or for tidal disruption) depend sensitively on the BH spin, a. The reason for this is that the angular velocity at the ISCO depends sensitively on the BH spin; GΩISCOMBH/c3 = 1/63/2 for the non-spinning BH whereas it is 1/2 for the BH of maximum possible spin, a = 1 [16, 186]. Here, the spin is non-dimensional and defined by \(a \equiv c{J_{{\rm{BH}}}}/GM_{{\rm{BH}}}^2\) where JBH is the angular momentum of the BH. As Equation (10) indicates, the increase of ΩISCO results in the increase of the critical value of Q for mass shedding (tidal disruption). Indeed, analyses [191, 225] indicate that the critical value for Q (or BH mass) increases by a factor of ∼ 15 if the spin is changed from zero to the maximum value (a = 1); e.g., for an incompressible fluid star, the maximum possible mass of a BH, which can cause mass shedding, was derived as
where C M ≈ 4.6 for a = 0, 7.8 for a = 0.5, 12 for a = 0.75, 19 for a = 0.9, and 68 for a = 1.
Another important finding is that the criteria for mass shedding (and tidal disruption) depend on the NS EOS even if the mass and radius of the NS are identical [225, 94]: NSs with stiffer EOS, (i.e., with high adiabatic index) have a relatively uniform density profile and are susceptible to tidal deformation, mass shedding, and tidal disruption by the BH tidal field. Consequently, condition (12) is modified by the EOS. In the calculation with compressible models [225, 94], the maximum possible mass of a BH, which can cause mass shedding, may be reduced by 10–20% for soft EOS (with the relatively small adiabatic index). This implies that not only the compactness of the NS but also its EOS, which is still unknown, is reflected in the tidal disruption event. General relativistic studies for quasi-equilibria of BH-NS binaries in addition show that the self-gravity of the NS significantly reduces the maximum mass of the BH for the onset of mass shedding (see Section 1.4 and Figure 22).
1.3 Why is the merger of BH-NS binaries important?
The merger of BH-NS binaries (more specifically, tidal disruption of a NS by a BH) is physically and astrophysically an important phenomenon, and deserves a detailed study, because of at least three reasons as follows.
-
Gravitational waves emitted during tidal disruption of a NS will bring us invaluable information about the radius and the EOS of the NS, because the orbital frequency at tidal disruption depends strongly on the compactness of the NS (GMNS/RNSc2), e.g., [107, 109]. The masses of the NS and the BH will be determined by the data analysis for gravitational waves emitted in the inspiral phase (see, e.g., [49] and also references cited in [96, 180]). If the NS radius could be determined or constrained from the observation of gravitational waves emitted during tidal disruption, the resultant relation between the mass and the radius of the observed NS may be used for constraining the EOS of the high-density nuclear matter [127, 220, 70]. Therefore, the gravitational-wave observation for BH-NS binaries will provide a new tool for exploring high-density nuclear matter, which is totally independent of standard nuclear experiments. The issue here is to theoretically clarify the dependence of gravitational waveforms on the NS EOS quantitatively; theoretical templates for a variety of possible EOS have to be prepared.
-
A tidally-disrupted NS may form a disk or torus of mass larger than 0.01 M⊙ with the density ≳ 1011 g/cm3 and the temperature ≳ 10 MeV around the remnant BH, if tidal disruption occurs outside the ISCO. A system consisting of a spinning BH surrounded by a massive, hot, and dense torus has been proposed as one of the likely sources for the central engine of a GRB [143, 232, 161, 142]. For the merger of BH-NS binaries, the resulting disk is likely to be compact and its mass is relatively small, of order 0.1 M⊙. Since the lifetime of such a disk is likely to be short (≲ 1 s), BH-NS binaries are proposed to be the progenitor of SGRB. Specifically, the merger of a low-mass BH and/or a rapidly-spinning BH, and its companion NS can be a candidate for the source of the central engine. According to the observational results by the Swift and HETE-2 satellites [142], the total energy of the SGRB is larger than ∼ 1048 ergs, and typically 1049–1050 ergs. This value may be explained if 1–10% of the thermal energy generated in a compact disk around a BH is converted to SGRB:
$$L = {\eta _{{\rm{eff}}}}{{G{M_{{\rm{BH}}}}\dot M} \over {{r_d}}} \approx 2 \times {10^{49}}{\rm{ergs/s}}\left({{{{\eta _{{\rm{eff}}}}} \over {{{10}^{- 2}}}}} \right)\left({{{10 \; G{M_{{\rm{BH}}}}} \over {r_{d}{c^2}}}} \right)\left({{{\dot M} \over {{{10}^{- 2}}{M_ \odot}/s}}} \right).$$(13)Here, ηeff is the efficiency, r d is the typical inner radius of the disk, and Ṁ is the mass accretion rate. The issue to be resolved is whether or not the mass and thermal energy of the torus formed after the merger are large enough for driving an SGRB of such huge total luminosity. The latest observations have also discovered that a longterm X-ray flare of duration ∼ 103–104 s is often associated with an SGRB [142]. Another more challenging issue is whether or not such an activity may be explained in the BH-NS merger scenario.
-
Material ejected from a tidally-disrupted NS may be important for understanding the observed abundances of the heavy elements that are formed by rapid neutron capture in the r-process [118]. One crucial question is whether it is possible for a fraction of material to escape from the system, because the situation is not well prepared for the mass ejection. Tidal disruption of a NS occurs typically at an orbital separation of ∼ 10GMBH/c2. For a test particle of mass m in a circular orbit around the BH with r = 10 GMBH/c2, the total energy is approximately GMBHm/2r = 0.05 mc2. For a free nucleon, 0.05 mc2 ≈ 50 MeV. Thus, the issues are, specifically, to answer whether it is possible to give about 50 MeV energy to each nucleon and, if possible, to clarify what the relevant process is.
1.4 General relativistic study of BH-NS binaries in quasi-equilibrium states
There are two computational tasks necessary to deeply understand the nature of the final coalescence phase of BH-NS binaries. One of the important tasks is to quantitatively determine the tidal-deformation effect on the orbital evolution in the late inspiral phase and the criterion for the onset of mass shedding (which is a necessary condition for tidal disruption). Determining the degree of the tidal deformation in close orbits is a crucial task for deriving phenomenological two-body equations of motion including the tidal-deformation effect (e.g., [50]).
In the framework of Newtonian gravity, a lot of effort was devoted to qualitatively determining the degree of the tidal deformation, its effects on the orbital motion, and the criterion of mass shedding [71, 111, 114, 213, 191, 217, 225, 94] as reviewed in Section 1.1. Although those approximate analyses are valuable for understanding the qualitative nature of coalescing close binaries, they cannot be appropriate for a quantitatively strict understanding, because coalescing BH-NS binaries in close orbits are in a highly relativistic state. A fully general-relativistic study is obviously required.
Motivated by this fact, numerical computations of quasi-equilibrium states in general relativity have been performed in the past 5 years by several groups, after early attempts, which were done in an approximate formulation of extreme mass ratios [19, 207] or in a preliminary formulation [138]. The first results in general relativity were published in 2006 by three groups: Taniguchi and collaborators [208], Grandclément [82, 83], and Shibata and Uryū [202, 203]. All these works solved the Hamiltonian and momentum constraint equations, and some components of Einstein’s equation (see Section 2 in detail). The first two groups employed the excision formulation (in which the region inside the BH apparent horizon is excised from the computational domain) and the last one employed the moving-puncture formulation. However, those early-stage results were unsatisfactory for accurately studying quasi-equilibrium sequences. Taniguchi and collaborators treated only mildly-relativistic NS and the numerical computation was not very accurate. The numerical code by Grandclément included some mistakes and the results were not correct. Shibata and Uryū constructed BH-NS binaries only including the corotating motion for the internal velocity field of the NS. However, in subsequent work, this situation was soon improved. Taniguchi and collaborators succeeded in accurately computing BH-NS binaries in quasi-equilibrium [209] and investigated their nature in detail [210]; Grandclément corrected his numerical code [83], and derived results as accurate as those of Taniguchi et al.; Kyutoku et al. succeeded in constructing BH-NS binaries with the irrotational velocity field for the NS [197, 106] developing a formulation originally proposed by Shibata and Uryū [202, 203]. All these groups computed sequences of quasi-equilibrium states and studied the nature of BH-NS binaries in close circular orbits (see Section 2).
Except for the early work of Shibata and Uryū [202, 203], all the computations have been done based on the spectral methods library, LORENE [79], because this enables high-precision computation, e.g., [27, 28, 84, 85]. (Note also that Grandclément and Taniguchi are two of the main developers of the LORENE library).
The Cornell-Caltech group also developed a numerical code, based on a spectral method for the precise computation of BH-NS binaries in quasi-equilibrium states [75], extending their original code to BH-BH binaries [158, 47, 40]. Up to now, this group has published quasi-equilibrium sequences only for the equal-mass case, which is not very realistic for BH-NS binaries, although their results for a variety of BH-NS binaries have been used as initial conditions for numerical-relativity simulations [58, 57, 74].
There are also two additional works on BH-BH/BH-NS binaries in quasi-equilibrium [216, 8]. However, these works primarily discuss a numerical method for computing BH binaries in quasi-equilibrium, and do not shown any computational results for BH-NS binaries. Hence, we do not review them in this article.
1.5 Non-relativistic simulation for the merger
The other important task is to clarify the evolution process in the last inspiral and merger phases. For this purpose, the numerical simulation is the unique approach because (at least) non-linear hydrodynamics including related physics has to be solved. The merger process of BH-NS binaries was first studied in the framework of Newtonian or pseudo-Newtonian gravity by several groups [95, 124, 123, 121, 122, 171, 169, 174]. These works have qualitatively clarified the tidal disruption process, the subsequent formation process of a BH-disk system, properties of the remnant accretion disk, gravitational waveforms emitted during the merger, and a fraction of matter ejected from the system. Earlier work [95, 124, 123, 121, 122, 171] was performed modeling BH by a point mass of Newtonian gravity. Because of the absence of the ISCO around the point mass in Newtonian gravity, the gravity in the vicinity of the BH was even qualitatively different from that in reality. They conclude that the NS might be tidally disrupted even in an orbit very close to the BH (well inside a radius of 6 GMBH/c2, which is unrealistic), and consequently, a massive remnant disk with mass larger than 0.1 M⊙ might be formed around the BH, irrespective of the mass ratio and the internal velocity field of the NS. In subsequent work [169, 174], the general-relativistic gravity of the BH was partly mimicked employing the Paczyński-Wiita potential for the point mass [152]. In this work, it was found that massive disk formation with mass larger than 0.1 M⊙ was possible only for a binary system composed of a low-mass BH or of a spinning BH for the case that the BH mass is not low [174]. These properties are qualitatively in agreement with those derived in recent fully general-relativistic simulations, and thus, for qualitatively or semi-qualitatively understanding the nature of the BH-NS merger, the pseudo-Newtonian simulation is shown to be helpful. In recent years, approximately general relativistic simulations were also performed by two groups [64, 65, 164]. The derived qualitative features in the merger of BH-NS binaries agree with those from pseudo-Newtonian studies as well as by the general relativistic studies described in Section 3.
Simulations in [95] were carried out incorporating detailed microphysical processes such as finite-temperature EOS and neutrino emission employing a neutrino leakage scheme. The neutrino luminosity from the BH-disk system formed in their simulations was found to be 1053–1054 ergs/s for the first 10–20 ms after the formation of the disks. This was the result for the case in which a hot and massive disk (of temperature ≳ 10 MeV and mass 0.2–0.7 M⊙) is formed. The high neutrino luminosity is encouraging for driving a SGRB via neutrino-antineutrino pair annihilation process. As remarked upon above, the massive disk formation in their model parameters would unlikely if general relativistic effects had been correctly taken into account. The high temperature also does not agree with a latest fully general relativistic result in which the simulation was performed with a similar EOS [57]. However, the results of [95] suggested for the first time that if such a massive disk was indeed formed, the resulting BH-disk system was a promising candidate for the central engine of SGRB. Also, their technique for handling the neutrino emission process becomes a useful guideline for detailed numerical studies in full general relativity (e.g., [183, 185]).
1.6 Stable mass transfer occurs or not
One interesting question for the final phase of BH-NS binaries is whether the stable mass transfer occurs in a close orbit; specifically, the question is whether the mass accretion from a NS to its companion BH proceeds for a time scale longer than the orbital period while escaping tidal disruption or merger. This could occur if the orbital separation does not decrease due to the presence of mass accretion. As discussed in several works and also indicated in the following, the answer is not trivial at all.
Clark and Eardley originally guessed that stable mass transfer could occur for a binary of mass ratio larger than a critical value (but smaller than a value determined by the presence of the ISCO; cf. Section 1.1), based on their analytic PN analysis [43]. In their analysis, the decrease of the orbital separation associated with gravitational-wave emission, which is one of the important processes in compact binaries of close orbits (see Equation (2)), was not taken into account. Cameron and Iben showed the importance of the gravitational radiation reaction for the onset of the stable mass transfer even in the close binary of white dwarfs [38, 22]. In addition, Benz et al. [22] show that if the stripped mass of a mass-shedding star forms a disk around the companion primary star (or contributes to the spin-up of the companion), the condition for the onset of the stable mass transfer is further restricted (see below).
The condition for the onset of stable mass transfer is roughly derived applying the analysis method of [38, 22] to BH-NS binaries. Here we will derive the approximate condition, briefly showing the essence of their analysis method. In the following, the analysis is performed in the Newtonian-gravity framework (except for the incorporation of the gravitational radiation reaction), and we assume that the mass element is not lost from the system nor forms a common envelope for simplicity; the material stripped from a mass-shedding NS is assumed to fall into the companion BH or to form the disk surrounding the BH, because this is indeed the case as found in general relativistic simulations. We also assume that the NS radius does not change, because it indeed depends only weakly on the NS mass as long as the mass is larger than ∼ 0.4 M⊙ (e.g., [116, 186] and Figure 10). For a very low-mass NS, the radius steeply increases with decreasing NS mass. We do not consider such a low-mass NS here.
In the Newtonian framework, the total angular momentum of the system is written as
where the mass of the disk around the BH is included in MBH. The time evolution of the angular momentum obeys the equation
where \({{\dot J}_{{\rm{GW}}}}\) is the loss rate of the angular momentum by the gravitational-wave emission, written assuming that the system is composed of point masses, as 6.4m0(μ/m0)2(Gm0/c2r)7/2, and Ṡ (≥ 0) denotes the total increase rate of the angular momentum of the BH and a disk of the BH. Ṡ is totally unknown; to determine it, a numerical simulation is necessary. Because it should be approximately proportional to ṀNS (the mass-shedding rate of the NS) and MBH, we write Ṡ = αsGc−1 ṀBHMBH, where we use ṀBH = −ṀNS. αs is a constant of order unity if all the stripped mass elements contribute to spin-up of the BH or to forming a disk; on the other hand, αs = 0 if the stripped mass element does not contribute to the spin-up and the formation of a disk. The assumption αs = 0 corresponds to the case in which we simply assume that the orbital momentum of the accreting material is simply added to the companion BH (the orbital angular momentum of the BH is increased).
Using Equation (14) with ṀBH = − ṀNS > 0, \({{\dot J}_{{\rm{orb}}}}\) is written as
and then, we obtain
for stable mass transfer to occur, ṙ has to satisfy ṙ ≥ 0. After a short calculation, the condition is written as
Here, the first and second terms on the right-hand side denote the effects of the gravitational radiation reaction, and of the spin-up or disk formation of the BH, respectively.
Mass shedding sets in when Condition (7) is satisfied. Thus, Equation (18) may be rewritten in the form
First, we consider the case of αs = 0. Then the condition can be written in the form
The left-hand side denotes the fraction of mass shedding in one orbital period. For stable mass transfer to occur, it should be much smaller than unity; at least smaller than unity. Here, 3.6 ≲ Q7/6(Q + 1)1/2/(Q − 1) ≲ 5.4 for 2 ≤ Q ≤ 10, and CΩ is likely to be ≲ 0.3. Thus, for a realistic value of \({\mathcal C} = 0.13 - 0.21\), the right-hand side of Equation (20) is ≲ 0.1. This suggests that stable mass transfer may occur in principle with a short time scale (in ∼ 10 orbits). However, we note that for a too large value of Q, mass shedding is unlikely to occur outside the ISCO, as illustrated in Section 1.1 (but for a high-spin BH, this may be avoided).
Next, we consider the case of αs = O(1). Then, the condition for stable mass transfer becomes
Here, 2.3 ≲ Q5/6(Q + 1)1/2/(Q − 1) ≲ 3.1 for 2 ≤ Q ≤ 10, and \(C_\Omega ^{1/3} \lesssim 0.7\). Thus, the term [⋯]−1 is likely to be much larger than unity for αs = O(1), and because of this presence of the term associated with αs = O(1), stable mass transfer is more strongly restricted. This indicates that the possibility for the occurrence of stable mass transfer depends strongly on the accretion process of the mass-shedding fluid elements, e.g., if the accreting material contributes mainly to the spin-up of the companion BH with αs = 1, the last term (the term [⋯]−1) is ≳ 3, and thus, the mass accretion rate has to be quite high for stable mass transfer to occur. However, with such a high mass-shedding rate, stable mass transfer would only for a short time scale, if at all. One interesting point is that to realize the onset of the stable mass transfer, the formation of the disk surrounding the BH or the spin-up of the BH has to be significantly suppressed.
Many Newtonian simulations, even when including the gravitational radiation reaction by the quadrupole formula, have found that stable mass transfer occurs (e.g., the works by Janka et al. and Rosswog et al. [95, 171]). Their results agree in a sense with that in early predictions such as in [43]. Janka et al. [95] show that the presence of the gravitational radiation reaction slightly prevents stable mass transfer, but this is not a very strong effect. However, their subsequent work [169, 174] shows that the discovery of stable mass transfer seems to be due to the lack of correct general relativistic physics. They performed an improved simulation in which general relativistic corrections to the gravity of the BH were phenomenologically taken into account via a pseudo-Newtonian prescription and showed that stable mass transfer was unlikely to occur, at least for the parameter space they considered. This shows that the gravitational radiation reaction alone does not prevent stable mass transfer, but this plus the strong two-body gravitational force in general relativity does. Remember that in the presence of general relativistic two-body effects, the onset of mass shedding outside the ISCO is possible only for a small value of Q, although for the stable mass transfer, a high value of Q is required. This conclusion agrees with the results in fully general relativistic simulations (see Section 3). General relativistic simulations, in which the mass accretion process to a BH is accurately followed, also show that the accretion of the stripped mass is used to spin up the BH. This is also an important property for preventing the onset of stable mass transfer (see Section 3).
It is worth noting that numerical simulations for BH-NS binaries with both a high BH spin with a > 0.9 and a high mass ratio with Q ≥ 10 have not been performed yet. For such a case, a strong repulsive force associated with spin-orbit coupling is likely to decrease the orbital radius of the ISCO and also to increase the inspiral time scale in a close orbit. This effect may help the onset of stable mass transfer, and thus, further studies are still required on this topic.
1.7 General relativistic study of late inspiral and merger
As illustrated above, general relativistic effects (the general relativistic attractive force between two bodies and resulting presence of the ISCO, spin-orbit coupling effect, and the general relativistic self-gravity in the NS) play a crucial role in the dynamics of a close binary system of a BH and a NS. Up to merger, the dynamics are primarily determined by the strong general relativistic gravity, and thus, the orbital evolution in a close binary, the merger and tidal disruption processes, the criterion of tidal disruption, and the evolution of the tidally-disrupted NS material depend strongly on general relativistic effects. Numerical computation in a fully general relativistic framework is obviously required for accurately and quantitatively understanding the nature of orbital evolution and the merger of BH-NS binaries; although non-general-relativistic works have provided a qualitative insight for these systems. Fortunately, the simulation in full general relativity is not a difficult task any longer, as reviewed in this paper. Now there is no reason to employ approximate frameworks for the study of this system.
Since 2005, which was the break-through year in the field of numerical relativity, the simulation of binaries composed of BHs has been feasible. Soon after the first success for the simulation of BH-BH binaries [162], work on the merger of BH-NS binaries was published [202, 203, 197, 62, 58, 63, 194, 57, 107, 108, 41, 74, 154, 109]. Shibata and his collaborators (hereafter the Kyoto/Tokyo (KT) group) performed a fully general relativistic simulation for a BH-NS binary merger for the first time, extending their earlier works for NS-NS binaries [193, 200, 201, 198, 199, 196]. Soon after the success of the KT group, the University of Illinois at Urbana-Champaign (UIUC) and Caltech/Cornell/CITA/Washington State University (CCCW) groups also performed simulations for BH-NS binary merger. The UIUC group extended their earlier work on NS-NS binaries [59], and the CCCW group extended their work for BH-BH binaries [30, 31, 181] incorporating the hydrodynamics equation solvers [57]. Subsequently, several scientific results have been derived recently by these groups. In addition, in 2010, the Louisiana State University/Brigham Young University/Perimeter Institute/Long Island University/Indiana University (LBPLI) and Albert Einstein Institute (AEI) groups published their first results for the BH-NS binary merger [41, 154]. All these groups will report with more sophisticated physics incorporating nuclear-theory-based EOS, microphysical processes, and magnetic-field effects in the near future. Thus, in the following sections, we focus only on reviewing the current status of the general relativistic studies (see also [56] for a review of the latest status of this field in 2010).
1.8 Outline and notation
This review is organized as follows. In Section 2, we review the current status of the study of quasi-equilibrium states of BH-NS binaries in general relativity. First, the formalisms for a solution of quasi-equilibrium states are described and then the resulting solution, its sequence, and implications are summarized. In Section 3, we review the current status of the numerical-relativity study of BH-NS binaries. In Section 3.1, we summarize the formulations, procedures, and numerical implementations employed in numerical simulations. In Section 3.2, the parameter space (composed of masses of BH and NS, BH spin, and the EOS of NS) investigated so far is summarized. In Sections 3.3–3.7, the numerical results for the evolution process throughout the late inspiral to the merger, tidal disruption processes, properties of the remnant formed after the merger, and features of gravitational waveforms and gravitational-wave spectra are summarized. We recommend that readers who are interested only in these simulation results read Section 3.3–3.7.
In this article, we adopt the following notations: Latin and Greek indices denote spatial and spacetime components, respectively. t denotes the coordinate time. In Section 2 and the Appendix A, the geometrical units of c = G = 1 are used, whereas in other sections, c and G are recovered.
2 Quasi-Equilibrium States
In this section, we first review formulations to construct BH-NS binaries in quasi-equilibrium, and then the representative numerical results derived so far.
2.1 Formulation
For a solution of BH-NS binaries in quasi-equilibrium, it is at least necessary to solve Einstein’s constraint equations and relativistic hydrostationary equations, supplemented by NS EOS. To derive a better model of quasi-equilibrium states, a part of Einstein’s evolution equation is also solved with an additional assumption. Until now, two approaches have been proposed to constructing BH-NS binaries in quasi-equilibrium. The main difference in those approaches comes from the method for handling the BH singularity. In one approach the BH singularity is eliminated from the computational domain by excising a coordinate sphere and by imposing equilibrium BH boundary conditions [47] (see also [10, 81] for a related isolated-horizon formalism). In the other approach, a BH is handled as a puncture [32]. In this approach, the metric quantities are decomposed into a singular part, which is written analytically and denotes contributions from a BH and a regular part, which is obtained by numerically solving the corresponding basic equations.
These two methods are separately explained below because they give different formulas. We refer to [208, 209, 210] for the excision approach and to [202, 203, 106] for the puncture one. For a more detailed discussion of the decomposition of Einstein’s equation and the formalism, we refer to [29, 231, 44], and for the hydrostatics [80, 214, 219].
2.1.1 Formulation in the excision approach
In the excision approach, Einstein’s equations in the conformal thin-sandwich formalism are solved for constructing quasi-equilibrium configurations [231]. The line element in the 3+1 form is written as
where \(\beta _{{\rm{com}}}^i\) is the shift vector seen by a comoving observer. We note that the coordinates in the comoving observer frame are usually chosen for convenience in this field (e.g., [80, 78]).
The spatial metric γ ij is further decomposed into a conformal factor ψ and a background spatial metric \({{\tilde \gamma}_{ij}}\) as
Here, the condition, \(\det ({{\tilde \gamma}_{ij}}) = 1\), is not always imposed. The shift vector seen by a comoving observer, \(\beta _{{\rm{com}}}^i\), can be decomposed as
where βi is the shift vector seen by an inertial observer and \(\beta _{{\rm{rot}}}^i\) is a rotating shift. The rotating shift is written as \(\beta _{{\rm{rot}}}^i = {(\Omega \times R)^i}\), where Ω is the orbital angular velocity vector of the binary system measured at infinity, and R a coordinate vector for which the origin is located at the center of mass of the binary system.
The extrinsic curvature is defined by
where ℒ n is the Lie derivative along the unit normal to the hypersurface Σ t . Following [229, 145], it is split into the trace K and the traceless part A ij as
The traceless part is rewritten as
where \({{\hat A}_{ij}} = {{\tilde \gamma}_{ik}}{{\tilde \gamma}_{jl}}{{\hat A}^{kl}}\). The Hamiltonian constraint then takes the form
where \({\tilde \Delta}\) denotes \({{\tilde \gamma}^{ij}}{{\tilde D}_i}{{\tilde D}_j}\), \({{\tilde D}_i}\) the covariant derivative with respect to \({{\tilde \gamma}_{ij}}\), and \({\tilde R}\) the scalar curvature with respect to \({{\tilde \gamma}_{ij}}\).
Equations (25), (26), and (27) yield
Inserting Equation (29) into the momentum constraint gives
In addition to the Hamiltonian and momentum constraints, the trace of the evolution equation of the extrinsic curvature is often employed as one of the field equations:
for a given condition for K and ∂ t K, this equation reduces to an elliptic-type equation for α, which possesses primary information of gravitational potential for an equilibrium or quasi-equilibrium configuration.
The matter terms in the right-hand side of Equations (28), (30), and (31) are derived from the projections of the stress-energy tensor T μν into the spatial hypersurface Σ t , defined by
for an ideal fluid for which
the following relation holds:
The set of Equations (28)–(31) has four functions that can be chosen freely; \({\partial _t}{{\tilde \gamma}^{ij}}\), ∂ t K, \({{\tilde \gamma}_{ij}}\), and K. For computing quasi-equilibrium states, one usually assumes the presence of a helical Killing vector, ξμ, and the absence of gravitational waves in the wave zone. Under these assumptions, it is natural to choose the time direction so as to satisfy ξμ = (∂/∂t)μ (in the comoving frame), and to set \({\partial _t}{{\tilde \gamma}^{ij}}\) and ∂ t K = 0. For the choice of K and \({{\tilde \gamma}_{ij}}\), two ways have been proposed. The first one is to choose a maximal slicing K = 0 and to adopt a flat metric \({{\tilde \gamma}_{ij}} = {f_{ij}}\), for simplicity. The other choice is to use the Kerr-Schild metric for \({{\tilde \gamma}_{ij}}\) and K in the vicinity of the BH or in the whole computational space. One of the advantages of choosing maximal slicing and the flat metric background is that the source term becomes simple and falls off rapidly for r → ∞ enough to obtain accurate results. The disadvantage is that it is not possible to construct the Kerr BH even with a distant orbit, and moreover, the set of Equations (28)–(31) may have non-unique solutions [159, 17, 224]. In particular, the spin of a BH has two values for the same spin parameter Ω r (see Equation (49) for the definition) [132]. The lower branch of the spin as a function of Ω r , which should be physically reasonable because it approaches to the Schwarzschild BH as Ω r → 0, can reach only a ≈ 0.85, much less than the maximum spin of a Kerr BH. The advantage of using the Kerr-Schild metric for \({{\tilde \gamma}_{ij}}\) and K is that one can calculate a spinning BH with nearly maximum spin, a ≃ 1. The disadvantage is that the source term becomes complicated and falls off slowly for r → ∞. Because of this situation, it is not easy to derive the results as accurately as those with the conformal three metric, if one adopts this background metric in the whole computational space [208]. To recover the accuracy, a modification of the Kerr-Schild metric seems to be necessary; the metric is chosen to be nearly the Kerr-Schild one in the vicinity of the BH, whereas away from the BH, the metric should approach exponentially a conformally-flat metric and a maximal slicing [75, 132].
In the following, we restrict ourselves to the case of maximal slicing and flat spatial background metric for simplicity. Then, Equations (28), (30), and (31) can be written as
where \(\underline \Delta\) and ∂ i denote the flat Laplace operator and the partial derivative, and Φ ≡ αψ. Note here that the shift vector \(\beta _{{\rm{com}}}^i\) was replaced by βi in Equation (41), because the rotating shift \(\beta _{{\rm{rot}}}^i\) does not contribute to the equation in the conformally-flat case. Equation (29) becomes
where we have replaced \(\beta _{{\rm{com}}}^i\) by βi for the same reason as above.
To solve the gravitational field equations (40), (41), and (42), it is necessary to impose appropriate boundary conditions on two different boundaries in the excision approach: outer boundaries at spatial infinity and inner boundaries on the BH horizons. Assuming asymptotic flatness, the boundary conditions at spatial infinity are written as
Inner boundary conditions arise from the excision of the BH interior. The assumption that the BH is in equilibrium leads to a set of boundary conditions for the conformal factor and the shift vector [47] (see also [40, 45] as well as the related isolated horizon formalism, e.g., [10, 81]). The boundary condition for the conformal factor is
where \({{\mathcal S}^i} \equiv {\psi ^{- 2}}{{\tilde {\mathcal S}}^i}\) is the outward pointing unit vector normal to the excision surface and h ij is the induced metric on the excision surface, \({h_{ij}} \equiv {\psi ^4}{{\tilde h}_{ij}} = {\gamma _{ij}} - {{\mathcal S}_i}{{\mathcal S}_j}\). The quantity L is computed from the projection of the extrinsic curvature K ij as L ≡ hij K ij . The boundary condition on the normal component of the shift vector is
Note that the quantity β⊥ is the the normal component of the shift vector in the comoving frame, \(\beta _{{\rm{com}}}^i\). The tangential component must form a conformal Killing vector of the conformal metric \({{\tilde h}_{ij}}\) on the excision surface. This can be achieved by choosing them to be Killing vectors of a 2-sphere,
where Ω r is an arbitrary parameter related to the spin of the BH, and \({{\tilde \xi}^i}\) is derived by solving the conformal Killing equation on \({{\tilde h}_{ij}}\). Because we choose a conformally-flat spatial background, Equation (49) can be rewritten as
Here \(\Omega _\tau ^j\) is a freely specifiable vector, related to the BH spin, and xk is a Cartesian coordinate centered on the 2-sphere. The quasi-local spin angular momentum associated with an approximate Killing vector of h ij is defined by
where ξi is the approximate Killing vector that is found by solving the Killing transport equations as described in [55, 40] ([55] described the original formulation and [40] reported a numerical result for BH-BH binaries based on the formulation of [55, 47]), or by a new alternative method for finding approximate Killing vectors of closed 2-spheres [48, 132]. \(\Omega _\tau ^j\) is iteratively determined until the quasi-local spin angular momentum of BH relaxes to a required value [40].
According to [47], the boundary condition on the lapse function can be chosen freely. For example, we can choose a Neumann boundary condition
on the excision surface.
2.1.2 Formulation in the puncture approach
A “puncture” method [32] was proposed by Brandt and Brügmann to describe multiple BH with arbitrary linear momenta and spin angular momenta, extending the original work by Brill and Lindquist [33]. A “moving-puncture approach” [39, 15] was revealed to be quite useful in dynamic simulations. Here, we describe the puncture approach for quasi-equilibrium in the context of BH-NS binaries, which was originally developed by Shibata and Uryū [202, 203] and subsequently modified by Kyutoku et al. [106]. The puncture approach employs a mixture of the conformal thin-sandwich decomposition and the conformal transverse-traceless decomposition of Einstein’s equations. The trace part of the extrinsic curvature is set to zero (maximal slicing) and the three metric is assumed to be conformally flat in the work so far.
The basic equations for the gravitational field are Equations. (40), (41), and (42) as in the excision approach. In the puncture approach, the metric quantities, which appear in Equations (40) and (42), ψ and Φ, are decomposed into an analytic singular part and a regular part. The former part denotes the contribution from a BH and the latter one is obtained by numerically solving the basic equations. Assuming that the puncture is located at \({r_{\rm{P}}} = x_{\rm{P}}^k\), ψ and Φ are given by
where MP and MΦ are positive constants of mass dimension, and \({r_{{\rm{BH}}}} = \vert {x^k} - x_{\rm{P}}^k\vert\) is a coordinate distance from the puncture. ϕ and η denote the regular parts of ψ and Φ, respectively, and are determined by solving elliptic equations (see Equations (59) and (61) shown below). The quantity MP is an arbitrarily-chosen parameter called the puncture mass, while MΦ is determined by the condition that the ADM mass (MADM) and the Komar mass agree,
Also, Â ij is decomposed into singular and regular parts as
Here \(K_{ij}^{\rm{P}}\) is the singular part, which denotes a weighted extrinsic curvature associated with the linear momentum, \(P_j^{{\rm{BH}}}\), and spin, \(S_j^{{\rm{BH}}}\), of the BH written by
\({l^k} = x_{\rm{P}}^k/{r_{{\rm{BH}}}}\) and ϵ ijk is the completely anti-symmetric tensor on Σ t .
W i denotes an auxiliary three-dimensional function and Wi = fijW j . The equation for W i is derived by substituting Equation (56) into the momentum constraint equation. Because the total linear momentum of the binary system should vanish1, the linear momentum of the BH, \(P_i^{{\rm{BH}}}\), is related to that of the companion NS as
where the right-hand side denotes the (minus) linear momentum of the NS.
The field equations to be solved are summarized as follows:
We note that in the puncture approach  ij is determined by solving Equation (56), not Equation (43), because  ij is not straightforwardly defined for the location with α = 0 when adopting Equation (43). In this approach, the elliptic equation for βi still has to be solved because βi is needed in solving hydrostatic equations.
Equations (59)–(62) are elliptic in type, and hence, appropriate boundary conditions have to be imposed at spatial infinity. Because of the asymptotic flatness, the boundary conditions at spatial infinity are written as
Here it is assumed that the equations are solved in the inertial frame.
In contrast to the case in which the excision approach is adopted, the inner boundary conditions do not have to be imposed in the puncture approach. This could be a drawback in this approach, because one cannot impose physical boundary conditions (e.g., Killing horizon boundary conditions) for the BH. However, this could also be an advantage, because we do not have to impose a special condition for the geometric variables, and as a result, flexibility for adjusting a quasi-equilibrium state to a desired state is preserved.
2.1.3 Hydrostatic equations
The hydrostatic equations governing quasi-equilibrium states are the Euler and continuity equations. The matter in the NS interior needs to satisfy those equations. There are several versions for deriving the hydrostatic equations [26, 9, 192, 215, 80, 204]. In this section, we review the version in [204, 219].
The equation of motion is written as
Assuming a perfect fluid, Equation (36), the term in the left-hand side of the equation of motion is written as
where T is the temperature, and s is the entropy per baryon mass. To derive the second line of Equation (65), we use an equation of local thermodynamic equilibrium,
Assuming that the entropy per baryon is constant everywhere inside the NS and using Equation (65), Equation. (64) yields
where we use the equation of rest-mass conservation,
Equation (67) can be further modified. Defining a spatial velocity υμ in the comoving frame, the 4-velocity is written as
where ξμ is a helical Killing vector, and we have a relation, υμn μ = 0. ut denotes the time component of uμ and is calculated through the normalization condition of uμ, uμu μ = −1. Substituting Equation (69) into Equation (67) and using the relation,
we obtain
if the fluid motion in a NS is synchronized with the orbital motion, i.e., the corotating case, we have υμ = 0. Thus, Equation (71) can be integrated once to yield
If the fluid motion in a NS is irrotational, we need to consider the vorticity of the fluid. The relativistic vorticity tensor is defined by
for the irrotational flow, ω μν = 0, there exists a scalar potential Ψ by which the term hu μ is expressed as
Inserting Equation (74) into Equation (71), we have
and thus,
or, in another form,
It is interesting to note that if we use the Cartan identity,
another form of the integrated Euler equation, e.g., Equation (33) in [80], is obtained. Because of the helical symmetry \({{\mathcal L}_\xi}(h{u_\nu}) = 0\) and the irrotational flow ω μ ν = 0, the Cartan identity yields
and thus,
This equation is equivalent to Equation (77).
The next task is to derive an equation for the velocity potential Ψ. The term in the left-hand side of the equation of continuity (68) is rewritten as
Using Equations (69), (74), and the expression for the helical Killing vector,
the equation of continuity (68) is rewritten as
where Equation (81) is used.
Finally, we comment on the prescription for determining the constant in the right-hand side of Equation (77). For this task, the central value of the quantities in the left-hand side is usually used. Here the center of the NS is defined as the location of the maximum baryon rest-mass density. Equation (77) includes one more constant, which should be determined for each quasi-equilibrium figure; the orbital angular velocity as found from Equations (24), (69), (74), and (82). The method for calculating it will be explained in the next Section 2.1.4.
2.1.4 Orbital angular velocity
The first integral of the Euler equation (77) includes information of the orbital angular velocity, Ω, through Equations. (24), (69), (74), and (82). Ω should be determined from the condition that a binary system is in a quasi-equilibrium circular orbit. In the following, we describe two typical methods referring to the rotation axis of the binary system as the Z-axis and to the axis connecting the BH’s and NS’s centers as the X-axis.
In one of two typical methods, a force balance along the X-axis is required. The force balance equation is derived from the condition that the central value of the enthalpy gradient for the NS is zero,
where \({{\mathcal O}_{{\rm{NS}}}}\) denotes the NS’s center at which the pressure gradient and self-gravitational force of the NS are absent. Thus, Equation (84) may be regarded as the condition that the gravitational force from the BH at the NS’s center is equal to the centrifugal force associated with the orbital motion, and hence, can be used to determine Ω for a given set of gravitational field variables.
In the other method, Ω is determined by requiring the enthalpy at two points on the NS’s surface along the X-axis to be equal to h = 1 on the surface. At these two points, the pressure is absent. Namely, the sum of the gravitational force from the BH, self-gravitational force from the NS, and the centrifugal force associated with the orbital motion is balanced. These two conditions may be regarded as the conditions that determine CE and Ω, and thus, Ω can be determined for a given set of gravitational field variables. The work by Taniguchi et al. [208, 209, 210, 214] confirmed that in both methods, an accurate numerical result can be computed with a reasonable number of iterations, and that the results by these two methods coincide within the convergence level of the enthalpy. Therefore, both methods work well.
2.1.5 Center of mass of a binary system
Equation (84) also depends on the location of the center of mass, because the rotating shift \(\beta _{{\rm{rot}}}^i\) includes R, which is the radial coordinate measured from the center of mass of the binary system. To determine the location of the center of mass of a binary system, in the framework of the excision approach, Taniguchi et al. [208, 209, 210, 214] and Grandclément [82, 83] require that the linear momentum of the system vanishes
where the maximal slicing condition, K = 0, is assumed. The essence of this condition is as follows: for a hypothetical orbital angular velocity, Ω, the total linear momentum of the system depends on the location of the center of mass, and hence, its location is determined by Condition (85). Once the location of the center of mass is determined in an iteration step, the positions of the BH and NS are moved, keeping the separation, in order for the center of mass of the binary system to locate on the Z-axis.
In the puncture approach, the situation is totally different from the above, because Condition (85) has already been used to calculate the linear momentum of the BH; see Equation (58) in Section 2.1.2. In this framework, there is no known natural, physical condition for determining the center of mass of the system. Until now, three methods have been employed to determine the center of mass. In the first method, the dipole part of ψ at spatial infinity is required to be zero [202, 203]. However, it was found that in this condition, the angular momentum derived for a close orbit of Ωm0 ≥ 0.03 is ∼ 2% smaller than that derived by the 3PN approximation for Q = 3. Because the 3PN approximation should be an excellent approximation of general relativity for a fairly distant orbit, as such Ωm0 ≈ 0.03, the obtained initial data deviates from the true quasi-circular state, and hence, the initial orbit would be eccentric.
In the second method, the azimuthal component of the shift vector βϕ at the location of the puncture is required to be equal to −Ω; a corotating gauge condition at the location of the puncture is imposed [197]. This method gives a slightly better result than that of the first method. However, the angular momentum derived for a close orbit of Ωm0 ≥ 0.03 is also ∼ 2% smaller than that derived by the 3PN relation for a larger mass ratio Q ≥ 2. The disagreement is larger for the larger mass ratio. Such initial conditions are likely to deviate from the true quasi-circular state and hence the orbital eccentricity is large as well.
In the last method, the center of mass is determined in a phenomenological manner: One imposes a condition that the total angular momentum of the binary system for a given value of Ωm0 agrees with that derived by the 3PN approximation [106]. This condition can be achieved by appropriately choosing the position of the center of mass. With this method, the drawback in the previous two methods, i.e., the angular momentum becoming smaller than the expected value, is overcome. Recent numerical simulations by the KT group have been performed employing initial conditions obtained by this method, and showed that the binary orbit is not very eccentric with these initial conditions (cf. Section 3.1.1).
2.1.6 Equations of state
A wide variety of EOS has been adopted for the study of quasi-equilibrium states of BH-NS binaries, which are employed as initial conditions of numerical simulations (see Section 3). However, the only EOS used for the study of quasi-equilibrium sequences has been the polytrope,
where κ is a polytropic constant and Γ is the adiabatic index. Hereafter, we review only the numerical results in this EOS.
For the polytropic EOS, we have the following natural units, i.e., polytropic units, to normalize the length, mass, and time scales:
Because the geometric units with G = c = 1 are adopted, the polytropic units Rpoly normalize all of the length, mass, and time scales.
Even though the EOS used for constructing sequences is only the polytrope, a lot of quasi-equilibria with several EOS have been derived as initial data for the merger simulations. We will summarize those initial data in Section 3.1.1.
2.1.7 Physical quantities
The several key quantities that are necessary in the quantitative analysis of quasi-equilibrium sequences are summarized in this section; the irreducible mass and spin of BH, the baryon rest mass of NS, the ADM mass, the Komar mass, and the total angular momentum of the system. It is reasonable to consider that the irreducible mass and spin of the BH and the baryon rest mass of the NS are conserved during the inspiral of BH-NS binaries. In addition, temperature and entropy of the NS may be assumed to be approximately zero because the thermal effects of not-young NS are negligible to their structure, i.e., it is reasonable to use a fixed cold EOS throughout the sequence. For such a sequence, the ADM mass, the Komar mass, and the total angular momentum of the system vary with the decrease of the orbital separation. These global quantities characterize the quasi-equilibrium sequence.
We classify the study by seven parameters and summarize in Table 1:
2.1.7.1 The irreducible mass of the BH
This is defined by [42]
where AEH is the proper area of the BH event horizon. Because it is not possible to numerically calculate AEH for a study of quasi-equilibrium configuration, people in the numerical relativity community approximate this area with that of the apparent horizon, AEH, which is computed from an integral on the apparent horizon S,
In the presence of a helical Killing vector, it is reasonable to consider that AEH agrees with Aeh (at least approximately).
In the framework of the excision approach, \({\mathcal S}\) corresponds to the excision surface. On the other hand, it is necessary to determine the apparent horizon in the framework of the puncture approach (although it is not a difficult task).
2.1.7.2 The spin of the BH
The spin is determined by the quasi-local spin angular momentum of the BH, which is given in Equation (51), i.e.,
2.1.7.3 The rest mass of the NS
This is defined by
where g is the determinant of g μν . Assuming the absence of mass loss, this should be conserved.
2.1.7.4 The ADM mass of the system
The ADM mass in isotropic Cartesian coordinates may be computed from
2.1.7.5 The Komar mass of the system
In the conformal thin-sandwich formalism [231] employed so far, the Komar mass is written as
where the shift vector is assumed to fall off sufficiently rapidly.
2.1.7.6 The total angular momentum of the system
York [230] defined this quantity by
where Xi is a spatial Cartesian coordinate relative to the center of mass of the binary system.
In addition, the definition of the linear momentum (which is usually set to be zero) is the same as Equation (85),
where the maximal slicing condition, K = 0, is assumed.
Then, the binding energy of the binary system is often defined by
where m0 is the ADM mass of the binary system at infinite orbital separation, m0 ≡ MBH + MNS (see Section 1.8 for the definition). For a non-spinning BH, Mbh coincides with the irreducible mass Mirr. For a spinning BH, the relation among MBH, Mirr, and a is given by [42]
In order to measure a global error in the numerical results, the virial error is often defined as the fractional difference between the ADM and Komar masses,
Here, we note the presence of a theorem, which states that for the helical symmetric spacetime, the ADM mass and Komar mass are equal (e.g., [76, 204]).
2.1.8 A mass-shedding indicator
To determine the orbit at the onset of mass shedding of a NS, Gourgoulhon et al. [80, 211, 212] defined a “sensitive mass-shedding indicator” (in the context of NS-NS binaries) as
Here, the numerator of Equation (99), (∂(ln h)/∂r)eq is the radial derivative of the enthalpy in the equatorial plane at the surface along the direction toward the companion, and the denominator, (∂(lnh)/∂r)pole, is that at the surface of the pole. The radial coordinate r is measured from the center of the NS. For a spherical NS at infinite separation, χ = 1, while χ = 0 indicates the formation of a cusp, and hence, the onset of mass shedding. Taniguchi et al. [208, 209, 210] analyze this parameter for identifying the mass-shedding limit of BH-NS binaries.
2.2 Current parameter space surveyed
Only a small parameter space has been surveyed for the study of quasi-equilibrium sequences. We classify the study by seven parameters in Table 1:
-
(1)
The EOS of the NS
-
(2)
The spatial background metric \({{\tilde \gamma}_{ij}}\) and the extrinsic curvature K
The notation of “CF” means the conformally-flat condition \({{\tilde \gamma}_{ij}} = {f_{ij}}\), and that of “M” denotes the maximal slicing K = 0.
The notation of “KS” means the Kerr-Schild metric. In this case, the extrinsic curvature K is also set to that derived from the Kerr-Schild metric.
-
(3)
The state of the fluid flow in the NS
The notation of “Co” means a corotating NS, and that of “Ir” denotes an irrotational NS.
-
(4)
The method to handle the BH, i.e., the excision or the puncture
The notation of “Pu” means the puncture approach, and that of “Ex” denotes the excision approach.
-
(5)
The BH spin a
-
(6)
The compactness of the NS \({\mathcal S}\)
-
(7)
The mass ratio Q
Because all the papers published so far employed the Γ = 2 polytrope for the EOS, we do not include the EOS in Table 1.
As found in Table 1, the surveyed parameter space is quite narrow, in particular for the EOS of the NS and the BH spin; complete sequences with a ≠ 0 have not yet been derived, and moreover, BH-NS binaries in quasi-equilibrium in which the BH spin takes a high value > 0.9 or the BH spin and orbital angular momentum vector misalign have not been studied yet. These are issues left for the future. For the initial data of the merger simulation, a slightly wider parameter space has been employed. We will summarize this in Section 3.1.1.
2.3 Numerical results
Several works, summarized in Table 1, have been done to calculate quasi-equilibrium sequences. In this section, we focus on the results reported in [210] because a systematic survey for a wider parameter space was done only there.
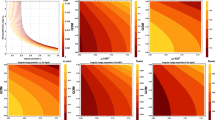
Figure 1 displays contours of the conformal factor ψ for a BH-NS binary with mass ratio Q = 3 and NS compactness \((J/m_0^2)\). This contour plot shows the configuration at the smallest orbital separation, for which Taniguchi’s code can achieve a converged solution. The thick solid circle on the left-hand side denotes the position of the excised surface (the apparent horizon), while that on the right-hand side denotes the position of the NS surface. A saddle point presents between the BH and NS, and for this close orbit, it is located in the vicinity of the NS surface, suggesting that the orbit of the binary is close to the mass-shedding limit. The value of ψ on the excised surface is not constant because a Neumann boundary condition (47) is imposed.
Contours of the conformal factor ψ in the equatorial plane for the innermost configuration with Q = 3 and \({\mathcal C} = 0.145\) shown in [210]. The cross “×” indicates the position of the rotation axis.
2.3.1 Binding energy and total angular momentum
Figure 2 shows the binding energy (Eb/m0) and the total angular momentum (\({{\bar M}_B} = 0.15({\mathcal C} = 0.145)\)) as functions of the orbital angular velocity (Ωm0) for a NS with baryon rest mass \({\mathcal C}\) and for mass ratio Q = 3. All the quantities shown are normalized to be dimensionless. The solid curves with the filled circles denote the numerical results, and the dashed curves, the results in the 3PN approximation [25]. The numerical sequences terminate at an orbit of cusp formation (i.e., at an orbit of the mass-shedding limit) before the ISCO is encountered, i.e., before a turning point (minimum) of the binding energy appears.
Binding energy Eb/m0 (left panel) and total angular momentum \(J/m_0^2\) (right panel) as functions of Ωm0 for binaries of mass ratio Q = 3 and NS mass \({{\bar M}_{\rm{B}}} = {(}0.15{)}({\mathcal C} = {(}0.145{)})\) [210]. The solid curve with filled circles show numerical results, and the dashed curve denotes the results in the 3PN approximation [25].
From the qualitative argument described in Section 1.1, the binary separation dms at the onset of mass shedding of a NS can be approximately derived as (see Equation (5))
If dms is greater by a sufficient amount than the ISCO separation dISCO, we may expect the NS to start shedding mass and to be tidally disrupted before being swallowed by the BH. Relation (100) suggests that the mass-shedding separation decreases with increasing mass ratio, Q, and compactness of the NS, \((J/m_0^2)\). It is natural to expect to encounter minima in the binding energy and total angular momentum for binaries with sufficiently large mass ratio and NS compactness. Figure 3 shows the binding energy (Eb/m0) and the total angular momentum \({{\bar M}_{\rm{B}}} = {(}0.15{)}({\mathcal C} = {(}0.145{)})\) as functions of the orbital angular velocity (Ωm0) for a NS with baryon rest mass \({\mathcal C} = 0.120\) and for Q = 5. The NS compactness is the same as, but the mass ratio is larger than, that shown in Figure 2. In this model, the binary encounters an ISCO before the onset of mass shedding, i.e., we see minima in the binding energy and angular momentum just before the end of the sequence.
Figure 3 shows that the turning points in the binding energy and the total angular momentum appear simultaneously to within numerical accuracy. This fact is more clearly seen in Figure 4 in which the binding energy versus total angular momentum for sequences of mass ratio Q = 5 but with different NS compactness is plotted. A simultaneous turning point in the binding energy and total angular momentum leads to a cusp in these curves. As suggested by Equation (100), turning points are not found for small compactness (e.g., the case of \({\mathcal C} = 0.145\)), since the sequences terminate at mass shedding before encountering an ISCO. However, for larger compactness, these curves indeed form a cusp. Note that 3PN sequences cannot identify mass shedding and therefore always exhibit turning points.
2.4 Endpoint of sequences
One of the most important questions in the context of BH-NS binaries is whether the coalescence leads to mass shedding of the NS before reaching an ISCO, or whether the NS is swallowed by the BH before the onset of mass shedding. This question arises from the perspective of gravitational-wave observations and from the relation with SGRB. Gravitational waveforms in the final inspiral phase depend strongly on this issue, and hence, a precise understanding of this is necessary to predict gravitational waveforms theoretically. For launching a SGRB, the formation of an accretion disk surrounding the BH is one of the most promising models, and can occur only if the NS is disrupted prior to reaching an ISCO.
Exploring this issue quantitatively requires dynamic simulations, and the results of such simulations are reviewed in Section 3. However, the study of quasi-equilibrium sequences can also provide a guide to where separation mass shedding or dynamic merger occurs. In the following, we summarize the quantitative insights obtained from the study of quasi-equilibrium sequences. Specifically, we will review qualitative expressions that may be used to predict whether a BH-NS binary of arbitrary mass ratio and NS compactness encounters an ISCO before shedding mass or not.
2.4.1 Mass-shedding limit
First, we summarize the results for the binary separation and the orbital angular velocity at which mass shedding from the NS surface occurs. In Newtonian gravity and semi-relativistic approaches, simple equations may be introduced to fit the effective radius of a Roche lobe [225, 94, 151, 60]. In [202, 203] a fitting equation is introduced for binaries composed of a non-spinning BH and a corotating NS in general relativity. In this section, we review how to derive a fitting equation from data in [210] for a non-spinning BH and an irrotational NS.
To derive a fitting formula, we need to determine the orbital angular velocity at the mass-shedding limit. However, it is not possible to construct cusp-like configurations by the numerical code used in [210], which is based on a spectral method and accompanied by the Gibbs phenomena. This is also the case for a configuration with smaller values of χ ≤ 0.5, even though a cusp-like configuration does not appear (here χ is a mass-shedding indicator defined by Equation (99)). Thus, the data points for such close orbits have to be determined by extrapolation. For this purpose, Taniguchi et al. [210] tabulated χ as a function of the orbital angular velocity and extrapolated the sequence to χ = 0 by using fitting polynomial functions to find the orbits at the onset of mass shedding. Figure 5 shows an example of such extrapolations for sequences of NS compactness \({\mathcal C}\) with mass ratios Q = 1, 2, 3, and 5 [210]. From the extrapolated results toward χ = 0, the orbital angular velocity at the mass-shedding limit is approximately determined for each set of \({\mathcal C}\) and Q.
Extrapolation of sequences for NS compactness \({\mathcal C} = 0.145\) to the mass-shedding limit (χ = 0). The thick curves are sequences constructed using numerical data, and the thin curves are extrapolated sequences [210]. Note that the horizontal axis is the orbital angular velocity in polytropic units, \(\bar \Omega = \Omega {R_{{\rm{poly}}}}\).
To derive a fitting formula for the orbital angular velocities at the mass-shedding limit for all the values of \({\mathcal C}\) and Q, the qualitative Newtonian expression of Equation (7) is useful. By fitting sequence data to this expression, Taniguchi et al. [210] determined the value of CΩ for Γ = 2 polytropic EOS as 0.270, i.e.,
or equivalently
Figure 6 shows the results of the fitting for the mass-shedding limit. The solid curve denotes Equation (101) and the points are the numerical results. The agreement is not perfect, but fairly good for Q ≥ 2.
It may be interesting to note that the value of CΩ = 0.270 is the same as that found for quasi-equilibrium sequences of NS-NS binaries in general relativity in [214] and of BH-NS binaries in general relativity where the NS is corotating in [202, 203]. The value of CΩ = 0.270 could be widely used for an estimation of the orbital angular velocity at the mass-shedding limit of NS in a relativistic binary system with Γ = 2.
2.4.2 Innermost stable circular orbit
One of the most important pieces of information for relativistic close binaries is the binary separation (or the orbital angular velocity) at which the minimum of the binding energy appears, corresponding to the ISCO. The minimum point is located by fitting three nearby points of the sequence to a second-order polynomial, because the numerical data is discrete and does not necessarily give the exact minimum.
A simple empirical fitting that predicts the angular velocity ΩISCO at the ISCO for an arbitrary companion orbiting a BH may be derived in the manner of [210]. In their approach, one searches for an expression with three free parameters that express ΩISCO as a function of the mass ratio Q and the compactness \({\mathcal C} = 0.5\) of the companion. Then the three parameters are determined by matching to three known values of ΩISCO, namely, (1) that of a test particle orbiting a Schwarzschild BH, ΩISCOm0 = 6−3/2 (for Q = ∞), (2) that of an equal-mass BH-BH system as computed in [40], ΩISCOm0 = 0.1227 (for Q = 1 and \({\mathcal C} = 0.1452\)), and finally (3) that of a BH-NS configuration as computed in [210], ΩISCOm0 = 0.0854 (for Q = 5 and \({\mathcal C}\)). A further requirement arises from the fact that for a test particle (with Q = ∞), the expression should be independent of the companion’s compactness. A good fit to the numerical data is found in [210] with the expression
as demonstrated in Figure 7. The exponents of Q and \({\mathcal C} = 0.145\) in Equation (103) are empirically determined by requiring that the fitted curves lie near the data points for all the models. The agreement is not perfect, but sufficient for finding the orbital angular velocity at the ISCO within ∼ 10% error.
2.4.3 Critical mass ratio
Combining Equations (102) and (103), we can identify the critical binary parameters that separate the final fates. The binary encounters an ISCO before reaching mass shedding or the NS reaches the mass-shedding limit. Figure 8 illustrates the final fate of BH-NS binaries for \({\bar \Omega}\). The solid curve denotes the orbital angular velocity at the mass-shedding limit, and the long-dashed one denotes it at the ISCO. As seen from Equations (102) and (103), both of these curves depend on the mass ratio Q, but in different ways, which leads to the intersection of the two curves. An inspiraling binary evolves along horizontal lines towards increasing \({{\tilde \gamma}_{ij}}\), starting at the left and moving toward the right, until reaching either the ISCO or the mass-shedding limit. After the binary reaches the ISCO for sufficiently large mass ratio, we cannot predict the fate of the NS, because it is in a dynamic plunge phase (see Section 3), but nevertheless the mass-shedding limit for unstable quasi-equilibrium sequences is included as the dotted curve in Figure 8. As shown in Figure 8, the model with mass ratio Q = 6 (dotted-dashed line) encounters the ISCO, while that of Q = 3 (dot-dot-dashed line) ends up at the mass-shedding limit. The intersection between the mass-shedding and ISCO curves marks a critical point that separates the two distinct fates of the binary inspiral.
An example of the boundary between the mass-shedding limit and the ISCO [210]. The selected model is the case of \({\mathcal C} = 0.145\). The solid curve denotes the mass-shedding limit, and the long-dashed one the ISCO for each mass ratio as a function of the orbital angular velocity in polytropic units. The dotted curve denotes the mass-shedding limit for unstable quasi-equilibrium sequences.
When we eliminate Ωm0 from Equations (102) and (103), we can draw a curve of the critical mass ratio, which separates BH-NS binaries that encounter an ISCO before reaching mass shedding, and vice versa, as a function of the compactness of the NS. The equation, which gives the critical curve is expressed as
and the curve that separates those two regions is shown in Figure 9. The solid curve denotes the critical mass ratio for each compactness. If the mass ratio of a BH-NS binary is larger than the critical one, the quasi-equilibrium sequence terminates by encountering the ISCO, while if smaller, it ends at the mass-shedding limit of the NS.
Critical mass ratio, which separates BH-NS binaries that encounter an ISCO before reaching mass shedding and undergoing tidal disruption, as a function of the compactness of NS. This figure is drawn for the model of Γ = 2 polytropic EOS [210].
2.5 Summary: quasi-equilibrium states
In this section, we have given an overview of the current status of the study of quasi-equilibrium BH-NS binary sequences in general relativity. Broadly speaking, two formulations have been proposed to construct quasi-equilibrium BH-NS binaries. The difference in these formulations comes primarily from the difference in the method for handling the BH singularity, the excision approach or the puncture approach. In these formulations, only five of ten components of Einstein’s equation are solved: constraint equations and the slicing condition. Deriving an improved formulation, in which full components of Einstein’s equation are solved, is left for the future (but see [204, 46] for proposed formulations and [218, 219] for a study of NS-NS binaries).
For the quasi-equilibrium sequences numerically derived so far, we mainly review those in [210], because it is the only systematic study. In particular, we highlight a curve of the critical mass ratio, which separates BH-NS binaries that encounter an ISCO before reaching mass shedding, and vice versa, as a function of the compactness of the NS. The result is shown in Equation (104) and in Figure 9. Such a critical curve clearly classifies the possible final fate of BH-NS binaries, which depends on the ratio and the compactness of the NS for a given EOS of NS and BH spin.
As seen in Table 1, the parameter space surveyed so far is quite narrow. A systematic study of quasi-equilibrium sequences has been done only for binaries composed of a non-spinning BH and an irrotational NS with Γ = 2 polytropic EOS. It is desirable that the remaining parameter space is systematically surveyed near the future. Systematic numerical results for such a study will be quite helpful for predicting the final fate of BH-NS binaries and for checking the results derived in numerical simulations. Specifically, it is necessary to study in detail quasi-equilibrium sequences of binaries composed of a spinning BH and a NS with an EOS other than single polytrope.
3 Numerical Simulations
By the year 2010, five groups — AEI, CCCW, KT, LBPLI, and UIUC groups — have succeeded in fully general-relativistic simulations for BH-NS binaries and provided a variety of the numerical results. The results of these groups agree qualitatively with each other and have clarified the basic picture for the merger and tidal disruption processes, although quantitatively, minor differences (e.g., on the remnant disk mass) have been reported. They have provided the criteria for tidal disruption, the final mass and spin of the BH left after the merger, the remnant disk mass, gravitational waveforms, and gravitational-wave spectrum. In the following sections, we review the methods of numerical relativity employed in these groups, the basic picture of the merger and tidal disruption processes clarified to date, and the resulting gravitational waveforms and spectra, separately.
3.1 Numerical method
3.1.1 Initial condition
As shown in Table 1, the studies of quasi-equilibrium and its sequences for BH-NS binaries have been performed by several groups. In the numerical simulations, quasi-equilibrium is employed as the initial condition (besides a minor modification of the quasi-equilibrium state, reviewed below). The five simulation groups, AEI, CCCW, KT, LBPLI, and UIUC, employ the quasi-equilibrium states derived by different groups as summarized in Table 2. Depending on the implementations on which each group relies, the type of the initial condition is different. Table 3 classifies the type of the initial data by the following six parameters:
-
(1)
The EOS of the NS
The notation of “Γ = 2” or “Γ = 2.75” means the single polytropic EOS with an adiabatic index of Γ = 2 or Γ = 2.75.
The notations of “PwPoly” and “SH” mean the piecewise polytropic EOS and the Shen’s EOS, respectively.
-
(2)
The spatial background metric \({{\tilde \gamma}_{ij}} = {f_{ij}}\) and the extrinsic curvature K
The notation of “CF” means the conformally-flat condition \({{\tilde \gamma}_{ij}}\), and that of “M” means the maximal slicing K = 0.
The notation of “KS” indicates the Kerr-Schild metric. In this case, the extrinsic curvature K is also set to that derived from the Kerr-Schild metric.
-
(3)
The state of the fluid flow in the NS
The notation of “Co” means a corotating NS, and that of “Ir” an irrotational NS.
-
(4)
The method to treat the BH, i.e., the moving puncture or the excision
The notations of “Pu” and “Ex” mean that the moving-puncture and the excision approaches are used in the numerical simulation, respectively. “ExPu” means that the initial condition is prepared in the excision approach, but the simulation is done in the moving-puncture formulation (see below).
-
(5)
Presence or absence of the BH spin a and misalignment angle θ between the spin axis and orbital angular momentum vector.
-
(6)
The mass ratio Q
When a quasi-equilibrium configuration constructed by the excision approach is used as initial data for a simulation code based on the moving-puncture approach, one more step is needed before starting the simulations because the data inside the BH excision surface does not exist, and thus, one needs to fill the BH interior by extrapolating all field values radially from the excision surface toward the BH center. In the extrapolation procedure, one has to employ a method in which any constraint violation introduced inside the BH is not allowed to affect the exterior spacetime. Two groups proposed such a procedure [34, 61], and the UIUC group used the method they developed in their simulations [61].
Strictly speaking, the quasi-equilibrium derived in the framework of Section 2 is not realistic because an approaching radial velocity driven by gravitational radiation reaction is not taken into account. If we adopt such quasi-equilibrium data as the initial condition, the trajectories obtained in the numerical simulation usually result in a slightly eccentric orbit. One prescription to suppress this error is to choose an initial condition in which the binary separation is large enough that the effect of the radial velocity is not serious. Another method to reduce the eccentricity was proposed by the CCCW group [157, 75] as described in the following.
(1) At the beginning of their procedure, they prepare a quasi-equilibrium data, which has zero approaching velocity υ r = ȧ0r = 0 and orbital angular velocity Ω0. (2) The second step is to evolve the quasi-equilibrium initial data for at least one and a half orbits. Then one records the time derivative of the measured coordinate separation between the center of the compact objects, ḋ(t) and fits ḋ(t) to a function of the form
where the parameters A0, A1, B, ω, and ϕ are all determined by the fitting. The A0 + A1t part denotes the smooth inspiral, while the B sin(ωt + ϕ) part denotes the unwanted oscillations due to the eccentricity of the orbit. For a nearly circular Newtonian orbit, the eccentricity e of the orbit can be written as
where d0 = d(t = 0). This implies that reducing the orbital eccentricity is equivalent to reducing B. (3) The final step is to add the corrections to the approaching velocity ȧ0 and the orbital angular velocity Ω using the parameters, which appear in Equation (105). Such corrections should be chosen so that the eccentricity-induced initial radial velocity and radial acceleration can be removed. Namely, the initial radial velocity is changed as
and the initial orbital angular velocity as
Using the corrected approaching radial velocity and the orbital angular velocity for the initial step (1), they iterated the procedure and obtained a better initial data. They showed that going twice through the iterative method described above, the orbital eccentricity is reduced by about an order of magnitude.
3.1.2 Evolving metric
There are currently two formalisms for evolving the spacetime metric. One is the Baumgarte-Shapiro-Shibata-Nakamura (BSSN) formalism [140, 195, 18] together with the moving-puncture gauge condition [39, 15, 35, 136], and the other is the generalized harmonic (GH) formalism [129] (see also [77, 86, 162, 163]). The AEI, KT, and UIUC groups employ the BSSN formalism, while the CCCW and LBPLI [6] groups use the GH formalism. These two formalisms are different from the standard 3+1 formalism [230], which was found to be inappropriate in numerical relativity because stable and longterm numerical simulations are not feasible due to the presence of an unphysical growth mode excited even by a tiny numerical truncation error.
The BSSN formalism, the original version of which was first proposed by Nakamura in 1987 [140], is in a sense a modified version of the 3+1 formalism [230]. The essence in this formalism is to adopt not only the three metric (γ ij ) and the extrinsic curvature (K ij ) but also a conformal factor of the three metric (ψ or ϕ = log(ψ) or W = ψ−2 or χ = ψ−4), the trace part of the extrinsic curvature (K), and the first spatial derivative of the three metric (\({F_i} = {{\tilde \gamma}_{ij,j}}\) or \({{\tilde \Gamma}^i} = - {{\tilde \gamma}^{ij}}_{,j}\) where \({{\tilde \gamma}_{ij}}\) is the conformal three metric) as new independent variables, and then, to appropriately rewrite the basic equations using these new variables. With this prescription, the evolution equations for the conformal three metric, \({{\tilde \Gamma}^i}\), and the conformal traceless extrinsic curvature, Ã ij ≡ γ−1/3(K ij − K γij /3), are written in the form of simple wave equations. This prescription leads to avoiding the spurious growth of unphysical modes by numerical truncation errors and enables one to perform a stable and longterm evolution for a variety of systems. Typical basic equations are described in Appendix A.
The basic equations of the GH formalism are similar to those employed in the PN approximation [25]. Using the harmonic or generalized harmonic gauge condition,
where Hν is the arbitrary function, Einstein’s equation is written in a hyperbolic form of the spacetime metric g μν . The main modification, analogous to the introduction of F i or \({F_i} - {{\tilde \gamma}_{ij,j}} = 0\) in the BSSN formalism, is treating H ν as independent functions. These may be either the functions themselves or determined by evolution equations. This is essential for the stable and longterm evolution of the system. The other modification is to introduce the first spatial derivative of the metric components as new independent variables D iμν = ∂ igμν to make the GH formulation first-order [129].
In both formalisms, the number of constraint equations is increased as a result of defining the new variables, in addition to the Hamiltonian and momentum constraints. For the BSSN formalism, \({\rm det}({{\tilde \gamma}_{ij}}) = 1,{{\tilde \gamma}^{ij}}{{\tilde A}_{ij}} = 0\), and \({{\tilde \Gamma}^i} + {{\tilde \gamma}^{ij}}_{,j} = 0\) or \({\kappa _i}\rho _i^{{\Gamma _i}} = {\kappa _i}_{+ 1}\rho _i^{{\Gamma _{i + 1}}}\) are new constraints. For the GH formalism, D iμν − ∂ i g μν = 0 is a new constraint.
3.1.3 Evolving a black hole
For handling a BH, the original BSSN formalism was not satisfactory. Re-defining a spatial con-formal factor [39], adopting more than fourth-order finite-differencing schemes, and employing an appropriate moving-puncture gauge condition [39, 15, 221, 35] are required for evolving BHs accurately and stably. In such a BSSN-puncture formulation, we choose a BH spacetime, which is free of the true singularity [32]. Although a coordinate singularity may appear in the center of the BH, this can be effectively (and, in a sense, fortunately) excised in the moving-puncture gauge condition [88]. Consequently, one can evolve the whole computational region without artificially excising inside the BH horizon (i.e., without special numerical treatments for the inside of the BH horizon).
On the other hand, in the code of the CCCW and LBPLI groups using GH formalism, the gauge, similar to the moving-puncture gauge, has not yet been developed. These groups employ the excision technique, i.e., a region inside the apparent horizon is cut out of the computation domain and replaced with an inner boundary. Pretorius has successfully simulated orbiting BH-BH binaries using the GH formalism with excision for the first time [162, 163]. Subsequently, the CCCW group has successfully simulated a longterm inspiral and merger of BH-BH binaries using a high-accuracy spectral method [181, 206], verifying that this technique is also robust for handling BH spacetimes.
3.1.4 Hydrodynamics
For the evolution of orbiting NS and a disk surrounding BHs formed after the merger, hydrodynamics (or magnetohydrodynamics) equations have to be solved. For a hydrodynamic simulation specifically, one has to solve the continuity equation for the rest-mass density ρ, the relativistic Euler and energy equations for the four velocity ¾ and internal energy ε (or h), i.e.,
where Tμν is the stress-energy tensor. For the perfect fluid, it is written as
for a magnetohydrodynamics simulation, we have to solve Maxwell’s equation as well. In ideal magnetohydrodynamics, only the induction equation for magnetic-field components should be solved [73].
If one needs to follow the evolution of the lepton number densities, the following additional continuity equations for the leptons (the electron number density and/or the total lepton number density) have to be solved
where Y a denotes a lepton number fraction per baryon and S a is the corresponding production/annihilation rates of the lepton in the baryon rest frame, which is associated with neutrino emission and absorption (e.g., [175, 176, 172, 173, 170, 146, 183, 184, 185]).
The hydrodynamic equation is schematically written in the form
where U represents the set of the evolved variables and Fi are the associated transport fluxes. The third term of Equation (115) denotes the source term, which is usually the coupling term between the hydrodynamic variables and geometric quantities or the first derivative of the metric. The third term is evaluated in a straightforward manner, which usually does not cause numerical instabilities in a straightforward evaluation (as long as an appropriate time step is chosen). A careful treatment is required in handling the transport term [73]. The numerical scheme for the transport term employed in all the groups is similar. The CCCW, LBPLI, and UIUC groups employ the scheme of Harten, Lax, and van Leer (HLL) [89], the AEI group employs several schemes prepared in their Whisky library [13, 14, 11, 12], and the KT group employs the scheme of Kurganov and Tadmor [105]. In handling the transport term, one further needs to determine the method of the interpolation by which the values of hydrodynamic quantities at the cell surfaces are specified. All these groups currently employ the third-order piecewise parabolic interpolation.
3.1.5 Equations of state
Employing realistic EOS for modeling NS is a key ingredient in accurately determining the final fate after the onset of the merger and in deriving realistic gravitational waveforms in the merger phase. However, the EOS of the nuclear matter beyond the normal nuclear density is still uncertain due to the lack of strong constraints obtained from experiments and observations (e.g., [115, 116, 117] and see [51] for a recent devlopment). Hence, we do not know exactly the detailed physical state of NS such as density and composition profiles as functions of radius for a given mass and the relation between the mass and the radius.
Gravitational waveforms emitted in the tidal-disruption phase as well as properties of the remnant BH-disk system such as the mass and the typical density of the disk depend strongly on the EOS, as shown in the following. The primary reason for this is that these depend strongly on the relation between the mass and the radius of the NS, the sensitivity of a NS to the tidal force by its companion BH depends primarily on its radius, e.g., a NS of larger radii (with a stiffer EOS) will be disrupted at a larger orbital separation (or a lower orbital frequency; see equations in Section 1); if the tidal disruption of a NS occurs at a larger distance, more material will be widely spread around its companion BH, and consequently, a high-mass remnant disk is likely to be formed; also, the gravitational-wave frequency at tidal disruption, which will be one of the characteristic frequencies, is lower for a NS of larger radius.
In the study of binaries composed of NS, rather than require one to prepare a “realistic” EOS, we should consider exploring the possibility of determining the NS EOS by gravitational-wave observation, as discussed in [127, 220, 168, 70]. For this purpose, we need to prepare theoretical templates of gravitational waves employing a wide variety of possible EOS for the NS matter, and systematically perform a wide variety of simulations employing a large number of plausible EOS. Then, the next task is to determine what kinds of EOS should be employed in their theoretical work.
Thermal energy per baryon inside NS, except for newly-born ones, is believed to be much lower than the Fermi energy of the constituent particles, because a young NS is quickly cooled down by neutrino emission (e.g., [116, 99]). This implies that we can safely neglect thermal effects on the NS in the inspiral and early merger phases, and can employ a cold EOS, for which the pressure, P, the specific internal energy, ε, and other thermodynamic quantities are written as functions of the rest-mass density ρ. In particular, employing the cold EOS is appropriate for the case in which the merger does not result in the formation of a disk surrounding the remnant BH, i.e., for the case in which the NS is simply swallowed by the companion BH, because a heating process, such as shock heating, never plays a role. By contrast, to follow a longterm evolution of tidally disrupted material, which forms a disk around the remnant BH, the finite-temperature effects of the EOS and the neutrino cooling have to be taken into account. This is because the temperature of the disk material is likely to be increased significantly by shock or a longterm viscous heating, while the density of the disk is lower than that of the NS, and as a result, the Fermi energy is lowered, resulting in a situation where the roles of the pressures by degenerate electrons and thermal gas become less important and increasingly important, respectively.
Because the simulation for BH-NS binaries in general relativity is still in an early phase (by 2010), much work has been done with a rather simple (not very realistic) EOS. The often-used EOS in the early phase of this study within the numerical-relativity community is the Γ-law EOS,
with Γ = 2. In this EOS, the initial condition for the NS is determined by the polytropic EOS, P = κρΓ (see Section 2). However, this EOS is known to disagree with typical nuclear-theory-based EOS for a small value of Γ ∼ 2 (e.g., [107] and Figure 10).
The relation between the mass and the circumferential radius of a spherical NS with piecewise polytropic EOS for which parameters are described in Table 4. For comparison, the curve for the Γ = 2 polytropic EOS with κ/c2 = 2 × 10−16 in cgs units is also plotted (dotted curve). The figure is taken from [107]. Note that if the observational result of [51] (if the presence of an ≈ 1.97 M⊙ NS) is confirmed by 100%, some of the soft EOS displayed here will be ruled out.
A better choice is to employ a piecewise polytropic EOS. This is a phenomenologic ally parameterized EOS, which approximately reproduces cold nuclear-theory-based EOS at a high density (above the nuclear density) only with a small number of polytropic constants and indices [167, 168, 150] (see also [87, 128]), i.e.,
where n is the number of the pieces used to parameterize an EOS and ρ i denote boundary densities for which appropriate characteristic values are assigned. Here, ρ0 = 0 and ρ n → ∞. κ i are the polytropic constants and Γ i the adiabatic indices for each piece.
At each boundary density, ρ = ρ i (i = 1, ⋯, n − 1), the pressure is required to be continuous, i.e., \({\mathcal C} = {M_{{\rm{NS}}}}/{R_{{\rm{NS}}}}\). Thus, if one gives k1, Γ i , and ρ i (i = 1, ⋯, n), the EOS is totally determined. For the zero-temperature EOS, the first law of thermodynamics (dε = −Pd(1/ρ) or dh = dP/ρ) holds, and thus, ε and h are also determined except for the choice of the integration constants, which are fixed by the continuity condition of ε (hence equivalently h) at each ρ i .
Recently, it has been shown that the piecewise polytropic EOS composed of one piece in the crust region and three pieces in the core region approximately reproduces most of nuclear-theory-based EOS at a high density [167]. Here, three pieces in the core region are required to reproduce a high-mass NS for which inner and outer cores could have different stiffness due to the variation of the properties of the high-density nuclear matter (ρ ≳ 2 × 1014 g/cm3). Thus, if one focuses on a NS of relatively low mass, a smaller number of pieces is acceptable; see [168, 107] for the two-pieces case. Table 4 lists the parameters employed in [168, 107], and Figure 10 shows the relation between the mass and the radius of a spherical NS for these piecewise polytropic EOS. We note that using a single polytrope for the low-density EOS is justified to the extent that the radius and deformability of the NS as well as resulting gravitational waveforms in the merger phase are insensitive to the low-density EOS.
In the presence of shocks during the merger phase, the assumption of zero-temperature breaks down. Thus, in addition to the piecewise polytropic part, a correction term has to be added. An often-used minimum prescription is to simply add the following term to the pressure [199, 168, 107]
where Γth is an adiabatic index for the thermal part, and εth = ε − εcold with εcold being determined by the piecewise polytropic EOS. This type of the piecewise polytropic EOS is employed by the KT group for a wide variety of parameters [107, 109].
To self-consistently take into account thermal effects, which play an important role in the evolution of a disk formed after tidal disruption occurs, the best way is probably to employ a finite-temperature EOS, which is derived by a detailed model based on nuclear physics. This type of EOS is usually described in table form, e.g., as
where T and Y e are the temperature and the electron fraction [119, 188, 189]. Here, approximately speaking, ρ is determined by the continuity equation (110), and T by the internal energy, which is essentially determined by the energy equation (112) in general relativity. Y e is determined by the continuity equation for the electron fraction (114). To solve this equation correctly, we have to take into account neutrino emission/absorption, by which the electron fraction is varied. Multidimensional numerical-relativity simulations have reached a level of incorporating the effects of neutrino emission/absorption only quite recently [183, 185]. Rather, most multidimensional numerical-relativity simulations have been performed without solving neutrino transfer equations and the equation for Ye [146, 53, 54, 74, 149], but an a priori assumption for Ye as a function of other variables such as ρ and T is imposed. Along this line (under the assumption that Ye is unchanged in the fluid rest frame or Ye is determined by the β-equilibrium), the CCCW group performed the first simulation taking into account the finite-temperature effect [57]. Recently, Sekiguchi has developed a leakage scheme of neutrinos in general relativistic simulation [183, 184, 185] and solves the equation for Ye taking into account neutrino emission for the first time. This technique will be applied to the simulation of BH-NS binaries in the near future.
3.1.6 Adaptive mesh refinement
There are two important length scales in the problem of compact binary coalescence. One is the scale associated with the size of compact objects, which is ∼ GMBH/c2 for BH and RNS ∼ 5–8GMNS/c2 for NS. The other is the wavelength of gravitational waves, λ. For a binary in a circular orbit of angular velocity Ω, the wavelength for the dominant quadrupole mode (l = |m| = 2 mode) is
where m0 = MBH + MNS. A longterm numerical-relativity simulation is typically performed with initial angular velocity Gc−3Ωm0 ≈ 0.02 for NS-NS binaries, and ∼ 0.03 for BH-NS binaries. Thus, λ is larger than Gm0/c2 by a factor of ≳ 100.
To accurately compute the evolution of an orbiting BH and NS resolving the structure of each object, the grid spacing should be smaller than Δ0 ∼ GMBH/20c2 and ∼ RNS/40, respectively. In addition, the outer boundary along each axis of the computation domain should be larger than the wavelength of gravitational waves to accurately take into account gravitational radiation reaction and to accurately extract gravitational waves in the wave zone. Then, if one adopts a uniform grid with grid spacing Δ0, the total grid number in one direction should be larger than
In three spatial dimensions, the required grid number is more than (2λ/Δ0)3. Thus, more than 10003 in the grid number is necessary. For such a simulation, a quite high computational cost is required even in the present computational resources. It should also be pointed out that in such studies, a survey for a large parameter space composed of the mass and the spin of the BH, and the mass and EOS of the NS is necessary (see Section 3.2). For this purpose, it is very important to make every effort to save computational costs for each run.
Therefore, to efficiently perform a large number of numerical simulations with the finite-differencing method, adaptive mesh refinement (AMR), such as that proposed by Berger and Oliger [23], is an indispensable technique. In this technique, one prepares several refinement levels of Cartesian boxes (or other geometrical domains) with different grid resolutions; usually in the smaller boxes, the grid resolution is higher. At such a fine refinement level, the BH and the NS are evolved with sufficiently high resolution with grid spacing ≲ Δ0. On the other hand, the propagation of gravitational waves, which have a wavelength much longer than the size of the compact objects, is followed in large-size boxes (in the coarser levels) with a large grid spacing, which is still much smaller than the gravitational wavelength (say, ∼ λ/10).
Mesh refinement techniques in numerical relativity have been developed by several groups (e.g., [93, 182, 35, 228]). The AEI and UIUC groups use the <monospace>Carpet</monospace> module of the <monospace>Cactus</monospace> code [182] developed primarily by Schnetter, the KT group the <monospace>SACRA</monospace> code [228] developed by Yamamoto, and the <monospace>LBPLI</monospace> group the <monospace>HAD</monospace> code [7]. Recently, two independent codes (<monospace>Whisky</monospace>, which employs <monospace>Carpet</monospace>, and <monospace>SACRA</monospace>) were compared, performing simulations of NS-NS binaries [14], and it was illustrated that the AMR scheme in <monospace>Carpet</monospace> and <monospace>SACRA</monospace> work well at the same level. The CCCW group employs a two-grid technique, which was originally proposed by the Meudon-Valencia-MPA team [52]. In this approach, geometric-field quantities are evolved with the multi-patch pseudo-spectral method and the hydrodynamic equations are solved using a standard finite-volume scheme on a second grid [58]. In solving the equations for the geometric field, the computational domain encompassing the local wave zone is prepared, while the hydrodynamic equations are solved in the region where the matter presents.
3.2 Current parameter space surveyed
There are many free parameters that specify a BH-NS binary; the mass and spin of the BH, and the mass of the NS. Furthermore, the EOS of the NS is still unknown, and thus, it should also be regarded as one of the free parameters. Here, the internal motion of the NS is believed to be close to an irrotational velocity field [24, 104] because the viscosity of the NS matter is too small to realize a corotational velocity field, and, in addition, the typical spin angular momentum of the NS (Prot =0.1–1 s) is slow enough that we can safely assume that the NS spin is zero (because an orbital period of ≲ 10 ms for m0 ≲ 10 M⊙ is much shorter than Prot). However, we have to accept a wide possible range for other parameters and EOS of NS. In particular, the mass and spin of a BH in a realistic binary system are totally unknown, and hence, a survey for a wide parameter space is required to fully understand the nature of BH-NS coalescence and to derive a complete catalog of possible gravitational waveforms.
In the first phase, all groups employed the Γ-law EOS in the form P = (Γ − 1)ρε with the special value of Γ = 2, for which the initial condition is prepared by using the polytropic EOS P = κρΓ. In this EOS, physical parameters are non-dimensional quantities such as mass ratio, Q = MBH/MNS, and compactness of the NS, \({\mathcal C}\), because κ can be freely chosen. Since 2009, several more plausible EOS have been employed by the KT and CCCW groups.
The early work of the KT group was done with the Γ-law EOS for a = 0 and for a wide range of Q and \(0.145 \leq {\mathcal C} \leq 0.178\); 1.5 ≤ Q ≤ 5 and \((Q,a,{\mathcal C})\). Since 2009, the KT group has employed a piecewise polytropic EOS [167, 150] with a wide variety of EOS parameters (see Table 4). Simulations have been systematically performed employing this EOS for a wide range of (\(0.12 \lesssim {\mathcal C} \lesssim 0.19\)) [107, 109]; 2 ≤ Q ≤ 5, −0.5 ≤ a ≤ 0.75, and \((Q,a,{\mathcal C})\). (Here, the negative value of the spin implies that the BH spin and orbital angular momentum vector are anti-parallel.)
The simulations of the UIUC group were performed employing the Γ-law EOS with Γ = 2. The UIUC group has chosen in total nine parameter sets for (\({\mathcal C} = 0.088\)) as follows; Q = 1, 2, 3, and 5, a = 0, −0.5, and 0.75, and \((Q,a,{\mathcal C})\) and 0.145. Simulations were performed for the relatively small value of NS compactness.
The CCCW group performed simulations employing two types of EOS; Γ-law EOS with Γ = 2 and 2.75, and Shen’s EOS, which is a tabulated EOS derived in a relativistic mean field theory [188, 189]. They focused on special parameter sets of (\({\mathcal C} \approx 0.145\)) as Q = 1 and 3, a = 0 and 0.5, and \((Q,a,{\mathcal C}) = (5,0.5,0.1)\) and 0.174. In their latest work, they focused on the case Q = 3 and a = 0.5, paying particular attention to the dependence of the merger process on the EOS and on the misalignment angle of the BH spin and orbital angular momentum axes.
The LBPLI group has performed one simulation to date, using the Γ-law EOS with Γ = 2, and with (\({\mathcal C} = 0.1 - 0.17\)) = (5, 0.5, 0.1) [41]. In their first work, the compactness was chosen to be small and not very realistic. In this simulation, magnetic fields in the ideal magnetohydrodynamics MHD approximation were incorporated, but they did not play an important role. The AEI group has performed simulations using Γ-law EOS with Γ = 2, and with Q = 5, a = 0, and \({\mathcal C}\) [154].
To summarize, the total number of simulations is still small, although a systematic survey is required to fully understand the complete picture of the coalescence of BH-NS binaries. In particular, many simulations were performed in a not very realistic setting using a simple Γ-law EOS and small values of \({\mathcal C} = 0.145\). As mentioned in Section 1, tidal disruption is more subject to the less compact NS, and hence, it should be in particular cautioned that a simulation with unphysically-small values of compactness may lead to an incorrect conclusion that tidal disruption and subsequent disk formation are easily achieved.
Nevertheless, the simulations performed so far have clarified a basic picture for the merger process of BH-NS binaries, the properties for the remnant, gravitational waveforms, and gravitational-wave spectrum. In the following, we summarize our current understanding of these topics based on work to date.
3.3 Merger process
3.3.1 Zero BH spin
As mentioned in Section 1, broadly speaking, the final fates of BH-NS binaries are divided into two classes. One in which the NS is tidally disrupted before it is swallowed by the companion BH and the other is that the NS is simply swallowed by the BH. Figures 11 and 12 display snapshots of the rest-mass density profiles and the location of the apparent horizon on the equatorial plane at selected time slices for two typical cases [107]. For these results, the NS are modeled by the piecewise polytropic EOS described in Table 4. Figure 11 illustrates the process in which the NS is tidally disrupted before the binary reaches the ISCO and then a disk is formed surrounding the companion BH. For this model, MBH = 2.7 M⊙, a = 0, MNS = 1.35 M⊙, and RNS = 15.2 km (EOS 2H); the mass ratio (Q = 2) is small and the NS radius is large. For this setting, the NS is significantly tidally deformed in close orbits, and eventually, mass shedding from an inner cusp of the NS sets in far outside the ISCO. After a substantial fluid element is removed from the inner cusp, the NS is tidally disrupted outside the ISCO. It should be emphasized that tidal disruption does not occur immediately after the onset of mass shedding in this case. Tidal disruption occurs for an orbital separation smaller than that for the onset of mass shedding.
Evolution of the rest-mass density profile in units of g/cm3 and the location of the apparent horizon on the equatorial plane for a model with MBH = 2.7 M⊙, a = 0, MNS = 1.35 M⊙, and RNS = 15.2 km (EOS 2H). This simulation was performed by the KT group. The filled circle denotes the region inside the apparent horizon of the BH. The colored panel on the right-hand side of each figure shows log10(ρ). This figure is taken from [107].
The same as Figure 11 but for a model with MBH = 4.05 M⊙, a = 0, MNS = 1.35 M⊙, and RNS = 11.0 km (EOS B).
After tidal disruption occurs, the material of the NS forms a one-armed spiral. As a result of angular momentum transport in the arm, a large amount of material spreads outward, and after the spiral arm is wound from the differential rotation, a disk of approximately axisymmetric configuration is formed around the BH located approximately at the center. However, because of the presence of a non-axisymmetric structure at its formation, however, the disk does not completely relax to an axisymmetric state in the rotational period ∼ 10 ms. Rather, a one-armed spiral of small amplitude is present for a long time, and helps gradually transporting angular momentum outward, resulting in a gradual mass infall into the BH. However, the mass accretion time scale is much longer than the rotational period, and hence, the disk remains quasi-stationary for;≫ 10 ms. This evolution process agrees qualitatively with that found in the study of the longterm evolution of BH-disk systems [90, 103].
The tidal disruption process as illustrated in Figure 11 is qualitatively common for the model with a low-mass BH or a large-radius NS or a high-spin BH. However, quantitative details depend on the parameters of the binary. For a small mass ratio (Q ∼ 2) with a = 0, the typical size of the disk (the region with ρ > 1010 g/cm3) is 50–100 km with maximum density ≳ 1012 g/cm3 for a disk of mass ∼ 0.1 M⊙ as shown in Figure 11. Thus, the disk is rather compact. The disk relaxes to a nearly axisymmetric configuration in a short time duration, approximately equal to the rotational period around the BH. We note that these properties depend on the parameter of the binary. For example, for a large mass ratio with a high BH spin (e.g., Q = 5 and a = 0.75), the typical size is also ∼ 100 km, but the maximum density is smaller than those for the smaller value of Q; the time scale until the disk relaxes to an axisymmetric configuration is relatively long. A remarkable point is that the tidal debris of relatively low density ∼ 1010 g/cm3 could be ejected to a distance of ≫ 100 km [63, 57, 41, 109], i.e., a wider but less dense disk is formed (see also Section 3.3.3).
Figure 12 illustrates the case in which the NS is not tidally disrupted before it is swallowed by the BH. For this model, MBH = 4.05 M⊙, a = 0, MNS = 1.35 M⊙, and RNS = 11.0 km (EOS B in Table 4). In this case, the NS is tidally deformed only in a close orbit. Then, mass shedding sets in for a too close orbit to induce subsequent tidal disruption outside the ISCO. As a result, most of the NS material falls into the BH approximately simultaneously. Also, the infall occurs from a narrow region of the BH horizon. These processes help exciting a non-axisymmetric fundamental quasi-normal mode (QNM) of the remnant BH. The mass of the disk formed after the onset of the merger is negligible (much smaller than 0.01 M⊙), because the BH simply engulfs the NS.
Generally speaking, the final fate depends on the location where mass shedding of the NS sets in. If the location is in the vicinity of or inside the ISCO, most of the NS material falls into the companion BH, and a BH with negligible surrounding material is the outcome. With the increase of the orbital separation at the onset of mass shedding, the mass of the material surrounding the BH increases. Note again that the mass shedding has to set in sufficiently outside the ISCO to induce tidal disruption, because tidal disruption occurs only after substantial mass is removed from the NS.
3.3.2 Nonzero BH spin
The effect of the BH spin significantly modifies the orbital evolution process in the late inspiral phase and merger dynamics, as first demonstrated by the UIUC group [63]. Figure 13 shows the trajectories of the BH and NS for models with Q = 3, \({\mathcal C} = 0.145\), and a = 0 (left) and a = 0.75 (right) [63]. The NS is modeled by the Γ-law EOS with Γ = 2. The initial orbital angular velocity is the same for two models. For the binary composed of a non-spinning (a = 0) BH and NS, the merger occurs after about 4 orbits, whereas for the case with a spinning BH (a = 0.75), it occurs after about 6 orbits. For the case with a spinning BH, the decreased rate of the orbital separation appears to be small. Qualitatively, these differences may be explained primarily by the presence of a spin-orbit coupling effect, which is accompanied by an additional repulsive force for a > 0 (and attractive force for a < 0), and thus, reduces the attractive force between two objects (see the equations of motion for two-body systems in the context of the PN approximation [102, 226, 100]). In the presence of this additional repulsive force, centrifugal forces should be reduced for a given orbital separation. This slows down the orbital velocity, and therefore, the luminosity of gravitational waves is decreased and orbital evolution due to gravitational radiation reaction is delayed (the lifetime of the binary becomes longer). In addition, the orbital radius at the ISCO around the BH is decreased (and the absolute value of the binding energy at the ISCO around the BH is increased) due to the spin-orbit coupling effect (e.g., [16]). This further helps to increase the lifetime of the binary because it evolves as a result of gravitational radiation reaction and hence has to emit more gravitational waves to reach the ISCO.
Trajectories of the BH and NS coordinate centroids for models with Q = 3, \({\mathcal C} = 0.145\), and a = 0 (left) and a = 0.75 (right). This simulation was performed by the UIUC group. The NS is modeled by the Γ-law EOS with Γ = 2. The BH coordinate centroid corresponds to the centroid of the BH, and the NS coordinate centroid denotes a mass center. This figure is taken from [63].
This longer lifetime for a binary with a spinning BH enhances the possibility of tidal disruption, and the final outcome is modified. Figure 14 displays the contour curves and the location of the remnant BH for the same models as in Figure 13. For both models, the NS is tidally disrupted outside the ISCO and a disk is formed. For the spinning BH case (a = 0.75), a more extended, more massive, and denser disk is the outcome. For the non-spinning case (a = 0), the disk mass is only ≈ 4% of the total rest mass whereas for a = 0.75, it is ≈ 13% (see Section 3.4 for details of the remnant disk). This is probably due to the effect that the physical radius of the ISCO (or specific angular momentum of a particle orbiting the ISCO) around the spinning BH is smaller than that for the non-spinning BH and also that the radial approaching velocity at tidal disruption is smaller for a spinning BH because of the repulsive nature of the spin-orbit coupling effect.
The CCCW group subsequently studied the effects of BH spin on the final remnant with several EOS [57]. They reached a similar conclusion about the orbital evolution and final outcome to that of the UIUC group even for the case in which BH spin is slightly smaller, a = 0.5. This conclusion was reconfirmed also by the KT group [109] for a wide variety of piecewise polytropic EOS and mass ratios. Therefore, a moderately large BH spin, a = 0.5, is substantial enough for modifying the merger process and enhancing the disk formation. The CCCW group also performed a simulation with a = 0.9 and \({\mathcal C} \lesssim 0.18\) [74] and found that tidal disruption occurs far outside the ISCO and the resulting disk mass is very high, ∼ 36% of the total rest mass (see Section 3.4).
The KT group also found that [109] for binaries composed of a high-spin BH (a = 0.75) and NS, tidal disruption may occur for a large value of mass ratio, Q ∼ 5, for a wide variety of NS EOS as far as it gives \({\mathcal C} = {(}0.144{)} - 0.173\). This implies that tidal disruption of a NS may be possible for a large BH mass over a wide area. In such case, the material of the tidally-elongated NS is swallowed from a relatively narrow region of the BH surface. As will be discussed in Section 3.6, this helps excite a non-axisymmetric fundamental QNM of the remnant BH. On the other hand, for the non-spinning BH case for which tidal disruption occurs only for a small BH, the material of a tidally-elongated NS is always swallowed by a wide region of the BH surface. This suppresses the excitation of non-axisymmetric QNM. This difference is reflected in gravitational waveforms and spectra, as predicted in [177, 178] (in which a BH perturbation study was performed).
To clarify the fact described above, Kyutoku et al. [109] generated Figures 15–17, which show the evolution of the rest-mass density profile for Q = 3, Mns = 1.35 M⊙, and EOS HB (cf. Table 4) with a = 0.75, 0.5, and −0.5, respectively. The evolution processes shown in Figures 15 and 17 are similar to those in Figures 11 and 12, respectively. Figure 15 shows the case in which mass shedding of the NS occurs at an orbit sufficiently far from the BH. Subsequently, the NS is extensively elongated, a one-armed spiral is formed, and then the spiral arm composed of dense material is wound around the BH. The material located in the outer region of the spiral arm forms a disk, while that in the inner region falls into the BH. The infall of the dense material proceeds from a wide region of the BH surface as seen in the fourth panel of Figure 11. By contrast, for a = −0.5 (see Figure 17), tidal disruption does not occur and more than 99.99% of the NS matter falls into the BH from a narrow region of the BH horizon and in a short time scale.
The type of merger process for a = 0.5 shown in Figure 16 is qualitatively new. Tidal disruption occurs in a relatively close orbit (in the vicinity of the BH ISCO). The subsequent evolution process is similar to that for a = 0.75, but the infall of dense NS material to the BH occurs from a relatively narrow region (see the second to fourth panels of Figure 16). Eventually, the infall proceeds from a wide region of the BH surface, but the density of the infalling material seems to be too low to enhance a QNM oscillation of the BH significantly (see the fifth panel of Figure 16). This feature is often found for a binary of high-mass ratio and high BH spin.
To date, three types of merger process have been found. Type-I: the BH mass is low or the BH spin is high, and the NS is tidally disrupted for an orbit far from the BH ISCO; Type-II: the BH mass is not low, the BH spin is small (or a < 0), and the NS is not tidally disrupted; Type-III: the BH mass is not low, the BH spin (a > 0) is high, and the NS is tidally disrupted for an orbit close to the BH ISCO. Their merger processes are schematically described in Figure 18. These differences in the infall process are well reflected in gravitational waveforms and spectra.
Schematic pictures for the three types of merger process that have been found to date. Left (type-I): the NS is tidally-disrupted and the extent of the tidally disrupted material is as large as or larger than the BH surface area. Middle (type-II): the NS is not tidally disrupted and simply swallowed by the BH. Right (type-III): the NS is tidally disrupted and the extent of the tidally disrupted material in the vicinity of the BH horizon is smaller than the BH surface area. The solid black sphere is the BH, the blue distorted ellipsoid is the NS, the solid red circle is the location of the BH ISCO, and the dashed circle is the location of the tidal-disruption limit. This figure is taken from [109].
In the latest work of the CCCW group [74], the effect of spin orientation, which is misaligned with that of the orbit rotation axis, was studied for the first time. They performed simulations for a = 0, 0.5, and 0.9, and Q = 3 with Γ-law EOS (Γ = 2), and found that the remnant disk mass decreases sensitively with increase of the inclination (misalignment) angle for given values of a and Q (see Figure 20). This is quite natural because the spin-orbit coupling force is proportional to S·L, where S and L denote BH spin and orbital angular momentum vectors, respectively, and the radius of the ISCO around the BH approaches that for a = 0 with increasing of the inclination angle. Thus, the BH spin effect becomes less important with the increase of the inclination angle. They also found that the inclination angle is significantly decreased after a substantial mass of the NS falls into the companion BH, implying that the angular momentum vector of the remnant disk misaligns only modestly with the BH spin vector (by ≲ 20°). This is also quite natural because the orbital angular momentum is as large as or larger than the spin angular momentum of the BH for small mass ratios like Q = 3. However, for a high value of Q for which the fraction of the BH spin angular momentum in the total angular momentum is large, this conclusion will be modified. The initial inclination angle will not be significantly modified and an inclined disk, which subsequently precesses around the spinning BH, may be the outcome.
3.3.3 Extent of remnant disk
A tail of a one-armed spiral formed at tidal disruption often extends far away from the BH, in particular for the case in which the BH spin is high. The CCCW group reported that for Q = 3, a = 0.5, and \(\sqrt {{l^3}/G{m_0}}\) (i.e., for realistic values of the compactness), a tidal tail of mass 0.01–0.1 M⊙ goes to a distance l = 200–2000 km away from the BH before falling back to the central region [57]. They also reported that the fall-back time scale was ∼ 200 ms for l = 2000 km assuming that the material obeys geodesic motion. Here, 200 ms agrees roughly with the dynamic infall time scale \(\sqrt {{l^3}/G{m_0}}\). This indicates that the time scale of mass accretion from the disk onto the BH is much longer than the rotational period of the disk in the vicinity of the BH ∼ 10 ms. The typical duration of SGRB is 0.1–1 s [142]. Such a time scale may be explained by the time scale of the fall-back motion.
The LBPLI group also estimated the fall-back time for their simulation with Q = 5, a = 0.5, and \({\mathcal C} = 0.16 - 0.18\) [41]. In their simulation, the compactness of the NS was assumed to be smaller than that for a realistic NS, and thus, the formation of the tidal tail can be significantly enhanced. They reported that for a large fraction of the material ∼ 0.05 M⊙, the fall-back time may be longer than 1 s. However, they followed the motion of the tidal tail only for a short time duration (16.3 ms; i.e., they did not show that the material really went far away, l ≳ 104 km), and in addition, did not describe the detail of the method for estimating the fall-back time. (Note that a fall-back time longer than 1 s is realized only for an element, which reaches a distance from the BH of l ≳ 104 km.) Hence, their conclusion should be confirmed by a longer-term simulation in the future. Their finding in the framework of numerical relativity that the disk can extend to a large distance ≫ 10 GM0/c2 for a high BH spin was qualitatively new.
The KT group performed simulations for MNS = 1.35 M⊙, Q = 2–5, a = 0.75 with several piecewise polytropic EOS [109]. They found that even for a binary with a NS of realistic compactness \({\mathcal C} \approx 0.145\), the disk can extend to ≳ 500 km (which is approximately the location of the outer boundary of the computational domain in their simulations). This conclusion agrees qualitatively with the previous results by CCCW and LBPLI. Thus, for the merger of a rapidly-spinning BH and a NS, it may be concluded that a widely-spread disk is formed, and the lifetime of the accretion disk will be fairly long ≳ 0.1 s. The KT groups also found that the density of the disk decreases with increase of Q (or the BH mass); for a high-mass BH, a widely spread but less dense disk is formed.
3.3.4 Effects of EOS
The dependence of the merger process on the NS EOS comes primarily from the fact that the NS radius depends sensitively on the EOS. For a NS with a large radius, tidal disruption (and subsequent disk formation) is more likely. This fact was clearly shown in the works by the KT group [107, 109], performed employing a variety of the piecewise polytropic EOS.
The EOS also determines the density profile of a NS. Even if the radius is the same for a given mass, the density profiles for two NS may be different if the hypothetical EOS is different. The KT group showed that a NS with a small adiabatic index for the core region, with which the density is concentrated in the central region, is less subject to tidal disruption than that with a larger adiabatic index (with relatively uniform density profile), even if the radius and mass are identical; e.g., for the piecewise polytropic EOS listed in Table 4, a NS with a smaller value of Γ2 is less subject to tidal disruption. The reason for this is that the star with a high degree of central density concentration is less subject to tidal deformation, as reviewed in Section 1.2.
The CCCW group performed a simulation incorporating a tabulated finite-temperature EOS for the first time [57]. The advantage of this approach is that one can determine the temperature and composition, such as electron fraction in the disk formed after tidal disruption occurs. This will be useful for discussing the possibility that the remnant BH-disk system could be a central engine of an SGRB. To avoid taking into account the effects of neutrino emission, they assumed that the system is in β-equilibrium or that the electron fraction is unchanged in the fluid-moving frame. In the former and latter, they assumed that the system is in either of the following two limiting cases; the weak interaction time scale is either much shorter or much longer than the dynamic time scale, respectively. They performed simulations focusing on the case a = 0.5 and Q = 3. Irrespective of the EOS, they found that the remnant disk is neutron rich with Y e ∼ 0.1−0.2 and the temperature is only moderately high (maximum is ∼ 10 MeV with the average ∼ 3 MeV) with the maximum density ∼ 1012 g/cm3 and disk mass ∼ 0.1 M⊙. Perhaps, because of the relatively low mass and density of the disk, the temperature is not as high as that found in a Newtonian simulation with detailed microphysics [95].
3.4 Properties of the remnant black hole and disk
During merger, NS material falls into its companion BH, and then, the mass and spin of the BH vary. Because a large fraction of the NS material falls into the BH for most of the numerical experiments performed so far and the total energy of gravitational waves emitted (EGW) is much smaller than the total mass energy of the system, the final BH mass becomes roughly MBH + MNS − Mdisk − EGW ≲ MBH + MNS = m0. (The disk mass Mdisk and EGW are less than 10% of the initial total mass m0.) Numerical results indeed show that the final BH mass is larger than 0.9m0.
The final BH spin depends sensitively on the mass ratio and initial BH spin. This can be understood by the following simple analysis. In Newtonian gravity, the total orbital angular momentum for two point masses in a circular orbit with an angular velocity Ω is
Thus, the non-dimensional spin parameter of the system is approximately written as
where we assume that the BH spin aligns with the orbital angular momentum vector. If the mass and angular momentum of the remnant disk, and loss by gravitational waves may be neglected, a f will be equal to the spin of the remnant BH. At the onset of the merger or at tidal disruption, the angular velocity becomes Gc−3Ωm0 ∼ 0.05−0.1, and thus, (Gc−3Ωm0)−1/3 is in a narrow range of ∼ 2.1–2.7. This implies that a f is primarily determined by Q and a.
Equation (123) gives rather qualitative estimate for the spin of the remnant BH. Nevertheless, it still gives a good approximate value of the final spin with the choice of (Gc−3Ωm0)−1/3 = 3 as large as the remnant disk mass is small. With this choice, a f = 0.67, 0.56, 0.48, and 0.42 for Q = 2, 3, 4, and 5 and for a = 0. These values agree with the results derived by the CCCW [74], KT [194, 107, 108], and UIUC [63] groups within the error of Δa = 0.01−0.02.
For a large BH spin with a ≳ 0.5, a disk of a large mass (≳ 0.1 M⊙) is often formed even for Q ∼ 3 − 5 (see below). In such cases, Equation (123) overestimates the final BH spin. However, this equation still captures the qualitative tendency of the final spin; e.g., for small BH spin, the final spin is determined by the value of Q and the larger values of Q results in smaller final BH spin; for larger values of Q with a large BH spin a ≳ 0.5, the final BH spin is primarily determined by the initial BH spin.
The mass and characteristic density of the remnant disk surrounding the BH depend sensitively on the mass ratio (Q), the BH spin (a), and the EOS (or the compactness) of the NS. Figures 19–21 illustrate this fact. Figure 19 displays a result of the disk mass as a function of the NS compactness for Q = 2 (left) and Q = 3 (right) for various piecewise polytropic EOS and for various values of a, reported by the KT group [109]. This shows that the disk mass decreases steeply and systematically with the increase of the compactness irrespective of a and Q.
Left: Disk mass at 10 ms after the onset of merger as a function of NS compactness \({\mathcal C}\) with various piecewise polytropic EOS and with various values of a for Q = 2. Right: The same as the left panel but for Q = 3. The simulations were performed by the KT group and the figure is taken from [109].
Left: Summary of the remnant disk mass as a function of the BH spin for a fixed EOS (Γ = 2 EOS), NS compactness \({\mathcal C} = 0.145\), and mass ratio (Q = 3), computed by the UIUC, CCCW, and KT groups. The vertical axis shows the fraction of the disk mass Mr>rAH/M B where MB is the baryon rest mass of the NS. “CCCWin” shows the results by the CCCW group with inclination angle of the BH spin, 40, 60, and 80 degrees (from upper to lower points). Right: The same as the left panel but for the disk mass in the solar mass unit for more compact NS \(({\mathcal C} \approx 0.172)\) with a piecewise polytropic EOS (HB). The simulation was performed by the KT group [109]. For both panels, the disk mass is measured at t ≈ 10 ms after the onset of the merger (for the Γ-law EOS, MNS is assumed to be 1.4 M∩).
Left: Disk mass as a function of NS compactness for various values of Q with a = 0.75. Right: The same as the left panel but for a = 0.5. These simulations were performed by the KT group and this figure is taken from [109].
The left panel of Figure 20 plots together the results obtained by the UIUC, CCCW, and KT groups for Γ = 2 EOS with \({\mathcal C}\) and Q = 3 (the revised result by the KT group is plotted here; results in early work by the KT group do not agree with the result shown here [228, 194]; see below for the reason). This shows that the disk mass increases steeply with BH spin (a) for given values of \({\mathcal C} \sim 0.17\) and Q. The results by these three groups agree approximately with each other for a = 0. The CCCW group showed for the first time that the disk mass decreases with the increase of the inclination angle of the BH spin, and toward the limit to 90 degree, the disk mass approaches to that of a = 0. The right panel of Figure 20 plots the results by the KT group for different compactness (using EOS HB with MNS = 1.35 M⊙; see Table 4). This shows again that the disk mass increases with the increase of the BH spin, and also that for high BH spin (e.g., a = 0.75), the disk mass is larger than 0.1 M⊙ even for Q = 5 with \(({\mathcal C} \approx 0.145)\).
Figure 21 shows disk mass as a function of NS compactness for a = 0.75 and a = 0.5 as performed by the KT group [109]. A steep decrease in disk mass with increasing compactness is found irrespective of the values of a and Q. Simulations for BH-NS binaries with a spinning BH for particular values of the compactness or mass ratio were also performed by the CCCW and UIUC groups for a = 0.5 and 0.75, respectively. The results of the CCCW group for a = 0.5 and Q = 3 with various EOS agree with those of Figure 21 within ∼ 10–20%. We note that the disk mass may be different in the different EOS even with the same compactness of the NS, because the density profile of the NS, and the resulting susceptibility to the BH tidal force is different. Thus, this disagreement is reasonable. Also, the results of the UIUC group for a = 0.75, Q = 3, and \({\mathcal C} = 0.145\) = 0.145 with the Γ-law EOS (the disk mass ∼ 0.15 MB) agree with the relation expected from Figure 21 within ∼ 20% error.
To clarify the dependence of the disk mass on relevant parameters, we consider three types of comparisons. First, we consider the case in which a, \({\mathcal C}\), and the EOS are fixed, but Q is varied. In this case, the disk mass monotonically decreases with the increase of Q for many cases. For example, for a = 0 and \({\mathcal C} = 0.145\) with Γ = 2 EOS, the disk mass is larger (smaller) than 0.01 MB for Q ≲ 4 (Q ≳ 4) [63, 74, 154]. However, we should point out the exception to this rule, because for the case in which a large-mass disk is formed, this rule may not hold. For example, the comparison between the left and right panels of Figure 19 shows that for relatively small compactness \({\mathcal C} \lesssim 0.16\), a large-mass disk is formed for high BH spins and the disk mass depends only weakly on the value of Q for given values of a and \({\mathcal C}\).
Second, we consider the case in which Q and \({\mathcal C}\) are fixed, but a is varied. The UIUC group compared the results for a = −0.5, 0, and 0.75 for Q = 3 and \({\mathcal C} = 0.145\) with the Γ-law EOS (Γ = 2), and the resulting disk mass at ∼ 10 ms after the onset of the merger is 0.008, 0.039, and 0.15 MB for a = −0.5, 0, and 0.75, respectively [63]. The CCCW group performed a similar study for a = 0, 0.5, and 0.9 for Q = 3 and \({\mathcal C} = 0.144\) with the Γ-law EOS (Γ = 2), and found that the disk mass at 10 ms after the onset of the merger is 0.034, 0.126, and 0.360 Mb for a = 0, 0.5, and 0.9, respectively [74]. Both groups found the systematic steep increase of the disk mass with the increase of the BH spin (cf. the left panel of Figure 20). This was also reconfirmed by the KT group [109] (see the right panel of Figure 19 and Figure 21).
Third, we consider the case in which a and Q are fixed, but the compactness, C, is varied. Systematic work was recently performed by the KT group [107, 108, 109], employing a piecewise polytropic EOS. Figures 19 and 21 show that the disk mass decreases monotonically with the increase of \({\mathcal C}\) for given values of a and Q. For producing a disk of mass larger than 0.01 M⊙ for \(a = 0,\,{\mathcal C}\) should be smaller than ∼ 0.18 for Q = 2 and ∼ 0.16 for Q = 3 according to their results. For a = 0.75, the condition is significantly relaxed.
Finally, the KT group [107, 108] found that the disk mass depends not only on the compactness but weakly on the density profile. For the NS with a more centrally concentrated density profile, the disk mass is smaller. The reason for this is that if the degree of the central mass concentration is smaller, tidal deformation is enhanced and it encourages earlier tidal disruption after the onset of mass shedding.
It is interesting to note that for a = 0.75 and MNS ∼ 1.4 M⊙, the mass of a disk surrounding a BH can be larger than 0.1 M⊙ for Q ≲ 4 with \({\mathcal C} = 0.18\) and for Q ≲ 5 with \({\mathcal C} = 0.17\). For Q = 2, the disk mass will be ≳ 0.1 M⊙ for any realistic NS with \({\mathcal C} \lesssim 0.20\). For a BH of higher spin, the disk mass will be even larger (cf. the left panel of Figure 20). In addition, the disk mass does not decrease steeply with the increase of Q for such a high spin. In particular, for a small value of \({\mathcal C}\), the disk mass depends very weakly on Q. All these results indicate that the disk mass is likely to be large even for a higher value of Q(≥ 5) with a high BH spin (a ≥ 0.75). The maximum density of the disk increases monotonically with the disk mass. For a disk mass larger than 0.1 M⊙, the maximum density is larger than 1012 g/cm3 for Q ≲ 4 and ∼ 1011 g/cm3 for Q = 5 [109]. Hence, a high-mass disk with a relatively small value of Q ≲ 4 is likely to be universally opaque against thermal neutrinos for the typical geometrical thickness of the disk; a neutrino-dominated accretion disk is the outcome and this is favorable for copious neutrino emission. This leads to the conclusion that the coalescence of BH-NS binaries with a high-spin BH with a ≳ 0.75 and Q ≲ 4 is a promising progenitor for forming a BH plus a massive disk system; that is the candidate for a central-engine of SGRB.
Before closing this subsection, we should note that different groups have reported different quantitative results for the disk mass in their earlier work, which has been improved upon. For example, the earlier work of the KT group presented a small disk mass [228, 194]. This is mainly due to an unsuitable choice of computational domain and partly due to a spurious numerical effect associated with insufficient resolution and an unsuitable choice of AMR grid. The first work of the UIUC group also underestimated the disk mass [62]. This is due to an unsuitable prescription for handling the atmosphere. However, these have been subsequently fixed.
Generally speaking, the quantitative disagreement is due to the numerics. First, the fluid elements in the disk have to acquire a sufficiently large specific angular momentum which is larger than that at the ISCO of the remnant BH. The material that forms a disk obtains angular momentum by a hydrodynamic angular momentum transport process from the inner part of the material. This implies that such a transport process has to be accurately computed in a numerical simulation. However, it is well known that this is one of the challenging tasks in computational astrophysics. Second, to avoid spurious loss and transport of the angular momentum, a high-resolution computation is required. However, the disk material is located in a relatively distant orbit around the central BH. In the AMR scheme, which is employed in all the groups, the resolution in this region is usually poorer than that in the central region. This might induce a spurious loss of angular momentum and resulting decrease of disk mass, even by a factor of ∼ 2. However, these issues are being resolved with the improvement of computational resources, the efficiency of the numerical code, and the skill for computation with the AMR algorithm. The left panel of Figure 20 shows as much.
3.5 Criteria for tidal disruption
As mentioned in Section 1, tidal disruption occurs after the onset of mass shedding and after a substantial fraction of the NS material is removed from the inner cusp by the BH tidal field. It is important to emphasize again that the condition of tidal disruption is in general different from that of mass shedding for BH-NS binaries and that tidal disruption could occur in a more restricted condition than that for mass shedding, as mentioned in Sections 1 and 2. To determine the condition of tidal disruption, a dynamic simulation (not a study of quasi-equilibrium or equilibrium) is necessary.
It is not easy to strictly determine the condition of tidal disruption, because its concept is not as clear as that of mass shedding. One way to determine the condition is to use the property of gravitational waveforms in the merger phase; if the “cutoff” frequency is smaller than the frequency of a quasi-normal mode (QNM) of the remnant BH, we may conclude that tidal disruption occurs (see Section 3.6 for details of the cutoff frequency). Another way is to use the property of the merger remnant; we may recognize that tidal disruption occurs if the mass of a remnant disk surrounding a BH is substantial, say larger than 1% of the total rest mass at t ∼ 10 ms after the onset of mass shedding. We employ both criteria here to determine whether tidal disruption occurs or not.
First, we summarize the criterion for the case in which the BH spin is zero (a = 0). In this case, the condition of tidal disruption depends strongly on the mass ratio and compactness of the NS. According to the criterion associated with a gravitational-wave spectrum (see Figure 28, as an example), the condition of tidal disruption is \({\mathcal C} \lesssim 0.19\) for Q = 2 and \({\mathcal C} \lesssim 0.16\) for Q = 3.
Figure 19, which displays the result of the disk mass for a = 0 with several piecewise polytropic EOS, also illustrates that the condition of tidal disruption depends strongly on the values of Q and \({\mathcal C}\): the approximate condition for a = 0 is \({\mathcal C} \lesssim 0.18 - 0.19\) for Q = 2 and \({\mathcal C} \lesssim 0.16\) for Q = 3. We note that for Q = 3, this conclusion is consistent with those of the CCCW [57] and UIUC [63] groups. These criteria agree approximately with those derived from the gravitational-wave spectrum. The AEI group studied the case of Q = 5 with Γ-law EOS (Γ = 2) and showed that the condition is \({\mathcal C} \lesssim 0.13 - 0.14\) for Q = 5 [154].
For a spinning BH, in particular for the case in which the spin vector aligns with the orbital angular momentum vector, the condition for tidal disruption is highly relaxed. Here, we focus only on the case in which the BH spin vector is aligned with the orbital angular momentum vector. From the disk mass as a function of compactness shown in Figure 21 derived by the KT group, we can read the criteria as follows. For Q = 2, tidal disruption occurs irrespective of the value of \({\mathcal C}(\lesssim 0.2)\) for a ≥ 0.5. However, for a counter-rotating spin (a = −0.5), the criterion for tidal disruption is significantly restricted (\(({\mathcal C} \lesssim {(}0.16{)})\)). For a = 0.75, tidal disruption occurs irrespective of the value of \({\mathcal C}(\lesssim 0.2)\) as far as Q ≲ 4.
Finally, we compare the conditions for tidal disruption and mass shedding for a = 0. Figure 22 plots threshold curves of tidal disruption, mass shedding in general relativity, and mass shedding in a tidal approximation in the plane of (\({\mathcal C}\), Q). If the value of Q or \({\mathcal C}\) is smaller than that of the threshold curves, tidal disruption or mass shedding occurs. The points with error bar approximately denote the numerical results for the criterion of tidal disruption, based on the results by the KT group for Q = 2, by the CCCW, KT, and UIUC groups for Q = 3, and by the AEI group for Q = 5. The solid and dashed curves denote the critical curves for the onset of mass shedding for Γ = 2 EOS in general relativity [209, 210], and for the incompressible fluid in a tidal approximation (see Equation (12)), respectively. This shows that, for a realistically compact NS, \(0.13 \lesssim {\mathcal C} \lesssim 0.21\), the condition for tidal disruption is more restricted than that for mass shedding. The primary reason for this is that for such large compactness with a = 0, tidal disruption occurs only for a small value of Q. For such a system, the time scale for gravitational radiation reaction is as short as the orbital period in close orbits. This indicates that at the onset of mass shedding, the radial approaching velocity induced by gravitational radiation reaction is high enough to significantly decrease (increase) the orbital radius (angular frequency) during the subsequent mass-shedding phase up to final tidal disruption. If the fraction of this decrease in the orbital radius is large enough to enforce the orbit inside the ISCO, tidal disruption is prohibited. This mechanism makes the condition of tidal disruption for BH-NS binaries more restricted than that of mass shedding.
A summary for the conditions of tidal disruption and mass shedding for a = 0 in the plane of \(({\mathcal C},Q)\). If the value of Q or \({\mathcal C}\) is smaller than that of the threshold curves shown here, they occur. The points with error bars (and the dotted curve) approximately denote the numerical results for tidal disruption, based on results by the KT group for Q = 2, by the CCCW, KT, and UIUC groups for Q = 3, and by the AEI group for Q = 5. The solid and dashed curves denote the critical curves for the onset of mass shedding for Γ = 2 EOS in general relativity [209, 210], and for the incompressible fluid in a tidal approximation (see Equation (12)), respectively.
On the other hand, if the value of \({\mathcal C}\) is small, tidal disruption may occur even for a large value of Q. With increase of Q, the ratio of the time scale of gravitational radiation reaction to the orbital period at the ISCO increases (e.g., Equation (2)). For such a high-Q case, the effect of orbital decrease by gravitational radiation reaction after the onset of mass shedding becomes relatively minor, and therefore, the critical curves of tidal disruption and mass shedding approach each other.
For a BH-NS binary with high BH spin, mass shedding may occur even for high mass ratio (say Q = 10 for a ≳ 0.9, e.g., Equation (12)). For such a case, the conditions for tidal disruption and mass shedding may approximately agree with each other. This point should be clarified through future study. If this is the case, the quasi-equilibrium study plays an important role in determining the condition of mass shedding, because this also gives the (approximate) condition of tidal disruption.
3.6 Gravitational waveforms In this section, the features of gravitational waveforms emitted by BH-NS binaries, found from numerical simulations to date, are summarized, showing the numerical results by the KT group [107, 109]. Waveforms of qualitatively similar features have been also derived by the UIUC [63] and CCCW groups [58].
3.6.1 Zero BH spin
Figure 23 displays the typical gravitational waveforms for a = 0, which clearly reflect the features of the orbital evolution and subsequent merger processes (tidal disruption or not) as described in the following. In the early inspiral phase in which r ≫ RNS and r ≫ GMBH/c2, two objects behave like point masses. In addition, general relativistic effects to the orbital motion are not extremely strong. For such a phase, the signal of gravitational waves is the chirp signal that can be well reproduced by the PN approximation for the two-body problem [25].
Gravitational waveforms observed along the axis perpendicular to the orbital plane for Q = 3 and a = 0 with very stiff (2H), stiff (H), moderate (HB), and soft (B) EOS. The simulation was performed by the KT group. The solid and dashed curves denote the numerical results and results derived by the Taylor-T4 formula. D is the distance from the source and m0 = MBH + MNS. The left and right axes show the normalized amplitude (c2Dh/Gm0) and physical amplitude for D = 100 Mpc, respectively. This figure is taken from [107].
For a close orbit in which the finite-size effect is still negligible but general relativistic gravity between two objects plays a role, it is known that the simple PN analysis fails to provide a precise waveform. Comparisons of the waveforms derived through PN analysis and through numerical computation for BH-BH binaries [36, 30, 31, 5, 179] propose that a better waveform is phenomenologically derived using the Taylor-T4 formula. This method requires a special summation method of PN high-order terms in the equations of motion, which include gravitational radiation reaction effects in an adiabatic approximation. First, one needs to calculate the evolution of the orbital angular velocity Ω(t) through X(t) = [Gc−3Ω(t)m0]2/3 up to 3.5PN order by solving the following ordinary differential equations [36]
where F(X) is a polynomial of X as \(1 + \Sigma _{i = 2}^7{a_i}{X^{i/2}}\) and a i denote coefficients (functions of mass and spin of compact objects). ν is the ratio of the reduced mass to the total mass m0, ν = Q/(1 + Q)2. For a solution of X(t), then, the orbital phase Θ(t) is derived by integrating the following equation
After X(t) and Θ(t) are obtained, the complex gravitational-wave amplitude h22 of (l, m) = (2, 2) mode is calculated up to 3PN order using the formula of [101].
Figure 23 shows that gravitational waveforms in the late inspiral phase before the onset of the merger (or tidal disruption) indeed agree with the result derived by the Taylor-T4 formula for the BH-NS binaries, as in the case of BH-BH binaries. This is natural because of the equivalence principle for general relativity [227]. (Note that in the first few wave cycles, the agreement is not very good. This is because the initial condition given for their simulation was not in an exact quasi-circular orbit.)
The waveforms may deviate from the prediction by the Taylor-T4 formula before the onset of the merger for a small value of Q or for a large NS radius. The reason for this is that the NS is tidally deformed by the BH, and, as a result, the pure Taylor-T4 formula, in which the tidal-deformation effect is not taken into account, is not a good formula for such a phase. The features of gravitational waveforms in the final inspiral phase are summarized later.
By contrast, for a sufficiently large value of Q or for a sufficiently compact NS, the tidal-deformation effect is negligible, and hence, the waveforms are quite similar to those for a BH-BH binary as mentioned above. For a small degree of tidal deformation and mass shedding, most of the NS material falls into the BH simultaneously (this case corresponds to type-II according to the definition of Figure 18). In such a case, a fundamental QNM of a BH is excited (see the waveform for the soft EOS in Figure 23), and the highest frequency of gravitational waves is determined by the QNM.
The degree of the QNM excitation depends strongly on the degree of tidal deformation and mass shedding. The primary reason for this is that a phase cancellation is concerned in the excitation; here, the phase cancellation is the amount that the gravitational waves emitted in a non-coherent manner (with different phases) interfere with each other to suppress the amplitude of gravitational waves [141, 187, 139]. With increasing degree of mass shedding, the phase cancellation effect plays an increasingly important role and the amplitude of the QNM-ringdown gravitational waves decreases. For the case in which a NS is tidally disrupted far outside the ISCO, this effect is significantly enhanced because the NS material does not simultaneously fall into the BH. Rather, a widely spread material, for which the density is much smaller than the typical NS’s density, falls into the BH from a wide region of the BH surface spending a relatively long time duration (this case corresponds to type-I according to the definition of Figure 18). Here, it is appropriate to point out why infall occurs from a wide region of the BH surface; the BH mass is small for the case in which mass shedding occurs for a = 0, and thus, the areal radius of the BH is smaller than or as small as the NS radius. All these effects are discouraging for efficiently exciting a QNM, and therefore, the amplitude of the QNM-ringdown gravitational waves is strongly suppressed for the case in which tidal disruption occurs (see the waveform for EOS 2H in Figure 23). For the case in which tidal disruption occurs, the highest frequency of gravitational waves is approximately determined by the orbital frequency at tidal disruption, not by the frequency of a QNM.
One important remark here is that this highest, characteristic frequency is not in general determined by the frequency at the onset of mass shedding. Even after the onset of mass shedding, the NS continues to be a self-gravitating star for a while and gravitational waves associated with an approximately-inspiral motion are emitted. After a substantial fraction of gravitational waves is emitted and thus, the orbital separation becomes sufficiently small, tidal disruption occurs. At such a moment, the amplitude of the gravitational waves damps steeply, and hence, the highest frequency of gravitational waves should be determined by the tidal-disruption event.
The qualitative features summarized above depend on the BH spin; for binaries composed of a BH of high spin, tidal disruption may occur for a high mass ratio, and hence, the infall process of the tidally-disrupted material into the BH may be qualitatively modified. This is well reflected in gravitational waveforms, as described in the next Section 3.6.2.
3.6.2 Nonzero BH spin
Gravitational waveforms are significantly modified in the presence of BH spin. Figure 24 plots gravitational waveforms for Q = 3 with the same stiff EOS (HB EOS) and with the same initial angular velocity (Gc−3Ωm0 = 0.030) but with different values of the BH spin. This obviously shows that with increasing the BH spin, the lifetime of the binary system increases and hence the number of wave cycles increases. This is explained primarily by the spin-orbit coupling effect (see also Section 3.3), which brings a repulsive force into the BH-NS binary for the prograde spin of the BH. Due to the presence of this repulsive force, the orbital separation of the ISCO (the absolute value of the binding energy there) can be smaller (larger) than that for the non-spinning BH. This effect increases the lifetime of the binary, and furthermore, enhances the chance for tidal disruption of the NS because a circular orbit with a closer orbital separation is allowed. Second, the repulsive force reduces the orbital velocity for a given separation, because the centrifugal force may be weaker for a given separation to maintain a quasi-circular orbit. The decrease of the orbital velocity results in the decrease of the gravitational-wave luminosity, and this decelerates the orbital evolution as a result of gravitational radiation reaction, making the lifetime of the binary longer and increasing the number of cycles of gravitational waves. We note that all these effects are also clearly reflected in the gravitational-wave spectrum, as is shown in Section 3.7.
Figure 24 shows that for a ≤ 0, a ringdown waveform associated with a QNM of the BH is clearly seen, whereas for a = 0.75, such a feature is absent. This reflects the fact that tidal disruption of the NS occurs for a = 0.75 far outside the ISCO, whereas it does not for a ≤ 0. For a = 0.5, tidal disruption occurs but a ringdown waveform associated with a QNM is seen. This is a new type of gravitational waveform. In this case, tidal disruption occurs near the ISCO and a large fraction of the NS material falls into the BH. The infall occurs approximately simultaneously and proceeds from a narrow region of the BH surface. This new type appears for the case in which the BH mass (or mass ratio Q) is large enough that the surface of the event horizon is wider than the extent of the infalling material, as explained in Section 3.3.2 (see Figure 18).
The inspiral waveform matches well to that of the Taylor-T4 formula for binaries composed of a spinning BH as well as for a non-spinning BH. Figure 24 also shows that matching is achieved as well as for a = 0, irrespective of the spin, except for the final phase just before the onset of the merger. As in the case of a = 0, the deviation of gravitational waveforms from the prediction by the Taylor-T4 formula is enhanced with increasing degree of tidal deformation, and with subsequent mass shedding and tidal disruption.
3.7 The Fourier spectrum of gravitational waves
3.7.1 Zero BH-spin case
The final fate of the NS in BH-NS binaries is clearly reflected in the spectrum of gravitational waves. General qualitative features of the gravitational-wave spectrum for BH-NS binaries composed of non-spinning BH are summarized as follows. For the early stage of the inspiral phase, during which the orbital frequency is ≲ 1 kHz (R/12 km)−3/2 and the PN point-particle approximation works well, the gravitational-wave spectrum is approximately reproduced by the Taylor-T4 formula. For this phase, the spectrum amplitude of \({h_{{\rm{eff}}}} \equiv f\tilde h(f)\) decreases as \({f^{- {n_i}}}\) where n i ≈ 1/6 for f ≪ 1 kHz and the value of n i increases with f for f ≲ 1 kHz (R/12 km)−3/2. As the orbital separation decreases, both the non-linear effect of general relativity and the finite-sized effect of the NS come into play, and thus, the PN point-particle approximation breaks down. When tidal disruption (not mass shedding) occurs for a relatively large separation (e.g., for a NS of stiff EOS or for a small value of Q), the amplitude of the gravitational-wave spectra damps above a “cutoff” frequency fcut. The cutoff frequency is equal to a frequency in the middle of the inspiral phase with fcut ∼ 1−2 kHz for this case (it is lower than the frequency at the ISCO). The cutoff frequency depends on the binary parameters as well as on the EOS of the NS. A more strict definition of fcut was given by the KT group and will be reviewed below.
By contrast, if tidal disruption does not occur or occurs at a close orbit near the ISCO, the spectrum amplitude for a high frequency region (f ≳ 1 kHz) is larger than that predicted by the Taylor-T4 formula (i.e., the value of ni decreases and can even become negative). In this case, an inspiral-like motion may continue even inside the ISCO for a dynamic time scale and gravitational waves with a high amplitude are emitted. (This property holds even in the presence of mass shedding.) This is reflected in the fact that \(f\tilde h(f)\) becomes a slowly varying function of f for 1 kHz ≲ f ≲ fcut, where fcut ∼2−3 kHz.
A steep damping of the spectra for f ≳ fcut is universally observed, and for softer EOS with smaller NS radius, the frequency of fcut is higher for a given mass of BH and NS. This cutoff frequency is determined by the frequency of gravitational waves emitted when the NS is tidally disrupted for the stiff EOS or by the frequency of a QNM of the remnant BH for the soft EOS. Therefore, the cutoff frequency provides potential information for a EOS through the tidal-disruption event of the NS, in particular for the stiff EOS.
Figure 25, plotted by the UIUC group [63], clearly illustrates the facts described above. The top panel (case E) plots the spectrum for Q = 1, in which the NS is tidally disrupted far outside the ISCO. In this case, the spectrum damps at f ∼ 1 kHz at which the tidal disruption occurs. The bottom panel (case D) plots the spectrum for Q = 5, in which the NS is not tidally disrupted. In this case, the steep damping of the spectrum at f ∼ 2 kHz is determined by the swallowing of the NS by the companion BH, and thus, the cutoff frequency is characterized by ringdown gravitational waves associated with the QNM of the remnant BH. Because the finite-sized effect of the NS is not very important in this case, the gravitational-wave spectrum is similar to that of the BH-BH binary merger with the same mass ratio (Q = 5; see the dashed curve). In the middle panel (case A), the cutoff frequency, at which the steep damping of heff sets in, is different from that for the BH-BH binary with the same mass ratio. This implies that tidal deformation and disruption play an important role in the merger process and in determining the gravitational waveform.
The gravitational-wave spectrum for Q = 1 (Case E), 3 (Case A), and 5 (Case D) with a = 0 and Γ-law EOS with Γ = 2. This simulation was performed by the UIUC group. The solid curve shows the spectrum of a 2.5PN and numerical waveforms, while the dotted curve shows the contribution from the numerical waveform only. The dashed curve is the analytic fit derived in [5] from analysis of BH-BH binaries composed of a non-spinning BH with the same values of Q as the BH-NS. The heavy solid curve is the effective strain of Advanced LIGO. To set physical units, a rest mass is assumed to be MB = 1.4 M⊙ (R ≈ 13 km) for the NS and a source distance of D = 100 Mpc. This figure is taken from [63].
As described above, the cutoff frequency at which the steep damping of the spectrum occurs will bring us the information for the degree of tidal deformation and where tidal disruption occurs in a close orbit just before the merger. The degree of tidal deformation and the frequency at which tidal disruption occurs depend on the EOS of the NS. This suggests that the cutoff frequency should have the information of the EOS. Motivated by this idea, the KT group performed a wide variety of simulations, changing the mass ratio, EOS, and BH spin, and systematically analyzed the resulting gravitational waveforms. Figure 26 plots the spectrum as a function of the frequency for Q = 2, MNS = 1.35 M⊙, and with a variety of EOS for a = 0. Irrespective of the EOS, the spectrum has the universal feature mentioned above. However, the cutoff frequency, at which the steep damping sets in, depends strongly on the EOS.
Spectra of gravitational waves from BH-NS binaries for Q = 2, a = 0, and MNS = 1.35 M⊙ with various EOS. The bottom axis denotes the normalized dimensionless frequency fm0(= Gfm0/c3) and the left axis the normalized amplitude c2 \({c^2}f\tilde h(f)D/G{m_0}\). The top axis denotes the physical frequency f in Hz and the right axis the effective amplitude \(f\tilde h(f)\) observed at a distance of 100 Mpc from the binaries. The short-dashed sloped line plotted in the upper left region denotes a planned noise curve of Advanced-LIGO [2] optimized for 1.4 M⊙ NS-NS inspiral detection (“Standard”), the long-dashed slope line denotes a noise curve optimized for burst detection (“Broadband”) and the dot-dashed slope line plotted in the lower right region denotes a planned noise curve of the Einstein Telescope (“ET”) [91, 92]. The upper transverse dashed line is the spectrum derived by the quadrupole formula and the lower one is the spectrum derived by the Taylor-T4 formula, respectively. This figure is taken from [107].
The features of gravitational-wave spectra for a = 0 are schematically summarized in Figure 27. Here, three curves are plotted assuming that the masses of the BH and the NS are all the same with a = 0 and with a relatively small value of Q, but the NS EOS is different. The curves (i)-a, (i)-b, and (ii) schematically denote the gravitational-wave spectra for the stiff, moderately stiff, and soft EOS. For (i)-a and (i)-b, the damping of the spectrum is determined by tidal disruption. In this case, the spectrum is characterized simply by exponential damping for f ≳ fcut. We refer to a spectrum of this type as type-I. For the case (ii), on the other hand, tidal disruption does not occur, and the cutoff frequency is determined by the QNM of the remnant BH. In this case, for a frequency slightly smaller than fcut, the amplitude of the spectrum slightly increases with the frequency, that is a characteristic feature seen for the spectrum of BH-BH binaries (e.g., [36]). We refer to a spectrum of this type as type-II.
Schematic figure for the gravitational-wave spectrum for the same masses of BH and NS with different EOS of NS for a = 0. For (i)-a, tidal disruption occurs far outside the ISCO. For (i)-b, tidal disruption occurs near the ISCO. For (ii), tidal disruption does not occur and the NS is simply swallowed by the BH. We refer to the spectra (i)-a and (i)-b as type-I and the spectrum (ii) as type-II. For a = 0 and \(0.13 \lesssim {\mathcal C} \lesssim 0.2\), the type-I spectrum is seen only for small values of the mass ratio with Q ≲ 3. The filled and open circles denote the cutoff frequencies associated with tidal disruption and QNM, respectively.
To quantitatively analyze the cutoff frequency and to strictly study its dependence on the EOS, the KT group [194, 107, 109] fits all the spectra by a function with seven free parameters
where \({{\tilde h}_{3{\rm{PN}}}}(f)\) is the Fourier spectrum calculated by the Taylor-T4 formula and f ins , fins2, fcut, σins, σins2, σcut, and A are free parameters. The first and second terms on the right-hand side of Equation (126) denote spectrum models for the inspiral and merger phases, respectively. These free parameters are determined by searching the minimum for a weighted norm defined by
where i denotes the data point for the spectrum.
Among these seven free parameters, they focus on fcut because it depends most strongly on the compactness \({\mathcal C}\) and the NS EOS. Figure 28 plots fcutm0, obtained in this fitting procedure, as a function of \({\mathcal C}\) for a = 0. Also the typical QNM frequencies, fQNM, of the remnant BH for Q = 2 and 3 are plotted by the two horizontal lines, which show that the values of fcutm0 for compact models (\({\mathcal C}\)) with Q = 3 agree approximately with fqnm and indicates that fcut for these models are irrelevant to tidal disruption. For Q = 3, fcutm0 depends on the EOS only for \(({\mathcal C} \lesssim 0.16)\). By contrast, fcutm0 for Q = 2 depends strongly on NS compactness, \({\mathcal C} \lesssim 0.16\), irrespective of MNS for a wide range of \({\mathcal C}\).
Gc−3fcut m0 as a function of \({\mathcal C} \lesssim 0.19\) in logarithmic scales. The solid line is obtained by a linear fitting of the data for Q = 2 and Γ2 = 3. The short-dashed and long-dashed lines show approximate frequencies of the QNM of the remnant BH for Q = 2 and Q = 3, respectively. This figure is taken from [107].
An interesting finding in [107] is that the following relation approximately holds for the identical value of Q,
Namely, fcutm0 is approximately proportional to \({{\mathcal C}^{3.9}}\). This is a note-worthy point because the power of \({\mathcal C}\) is much larger than a well-known factor 1.5, which is expected from the relation for the mass-shedding limit presented in Section 1 (cf. Equation (7)). (For binaries composed of spinning BH, this power is smaller than 3.9, but it is still much larger than 1.5 [109].) This difference indicates that the cutoff frequency is not determined simply by mass shedding. Qualitatively, this increase in the power is natural because the duration of a NS for the survival against tidal disruption after the onset of mass shedding is in general longer for a more compact NS due to a stronger central condensation of the density profile.
Figure 26 illustrates that fcut is rather high, ≳ 2 kHz, for a variety of EOS, and thus, the dependence of fcut on the EOS for a = 0 appears only for a high frequency. The reason for this is that for a = 0, tidal disruption can occur only for a small mass ratio (and thus for a small total mass) with a typical NS mass of 1.3−1.4 M⊙; see Equation (8). The effective amplitude of gravitational waves at f = 2 kHz is ∼ 2 × 10−22 for a hypothetical distance to the source of 100 Mpc. The amplitude is smaller than the noise level of advanced gravitational-wave detectors, but such a signal will be detectable to next-generation detectors such as Einstein Telescope [91, 92].
3.7.2 Non-zero BH-spin case
The gravitational-wave spectrum is qualitatively and quantitatively modified by the BH spin. In the following, we focus only on the case in which the BH spin and orbital angular momentum vectors align, because gravitational waves for the misaligned case have not yet been studied in detail. Figure 29 shows the same relation as in Figure 26 but for Q = 3, MNS = 1.35 M⊙ and a = 0.75, 0.5, 0, and −0.5 with HB EOS (cf. Table 4; left) and for Q = 4, a = 0.75, and MNS = 1.35 M⊙ with various EOS (right). The left panel of Figure 29 shows that the spectrum shapes for a ≤ 0, a = 0.5, and a = 0.75 are qualitatively different; for a ≤ 0, the exponential damping above a cutoff frequency, which is determined by the fundamental QNM of the remnant BH, is seen. In this case, tidal disruption does not occur. This is the type-II spectrum according to the classification in Figure 27. On the other hand, for a = 0.75, the cutoff frequency (fcut ∼ 1.5 kHz) is determined by the frequency at which tidal disruption occurs. This is the type-I spectrum according to the classification in Figure 27. The spectrum for a = 0.5 is neither type-I nor type-II. In this case, there are two typical frequencies. One is at f ∼ 2 kHz, above which the spectrum amplitude sinks, and the other is at f ∼ 3 kHz, above which the spectrum amplitude steeply damps. The first frequency is determined primarily by the frequency at which tidal disruption occurs, and the second one is the QNM frequency of the remnant BH. We call this new type of spectrum type-III (according to the definition of Figure 18). In the right panel of Figure 30, we summarize three types of gravitational-wave spectrum.
Left: The same as Figure 26 but for Q = 3, MNS = 1.35 M⊙, and a = 0.75, 0.5, 0, and −0.5 with a moderately stiff EOS (EOS HB). Right: The same as the left panel but for Q = 4, a = 0.75, and MNS = 1.35 M⊙ with various EOS. The thin dashed curves show the noise curves for LCGT, advanced LIGO, broadband-designed advanced LIGO, and Einstein telescope (from upper to lower). The figures are taken from [109].
Left: Schematic figure of the type-I gravitational-wave spectrum for a high-frequency side with different values of the BH spin but for the same masses of BH and NS, and NS EOS. With increase of the BH spin, the cutoff frequency decreases and the amplitude below the cutoff frequency increases. Right: Three types of the gravitational-wave spectrum. Type-I (i) and type-II (ii) are the same as those shown in Figure 27. Type-III (iii) is shown for the case in which the BH spin is high and the mass ratio (and thus the area of the BH horizon) is large. The filled and open circles denote the cutoff frequencies associated with tidal disruption and with a QNM, respectively.
For the type-III spectrum, we refer to the first (lower) typical frequency as the cutoff frequency in the following. In this definition, with increasing BH spin, the cutoff frequency decreases and the amplitude of the gravitational-wave spectrum for f ≲ fcut increases. These two effects are preferable for gravitational-wave detection by planned advanced laser-interferometric detectors, because their sensitivity is better for smaller frequencies around f = fcut. These quantitative changes come again from the spin-orbit coupling effect (see also Sections 3.3 and 3.6), as explained in the following.
Due to the spin-orbit coupling effect, which brings a repulsive force into BH-NS binaries (for the prograde spin), the orbital velocity for a given separation is reduced, because the centrifugal force may be weaker for a given separation to maintain a quasi-circular orbit. Due to the decrease of the orbital velocity (a) the orbital angular velocity at a given separation is decreased and (b) the luminosity of gravitational waves is decreased. Effect (a) results in the decrease of the cutoff frequency at which tidal disruption occurs. Effect (b) decelerates the orbital evolution as a result of gravitational radiation reaction, resulting in a longer lifetime of the binary system and in increase in the number of the gravitational-wave cycle. This effect increases the amplitude of the gravitational-wave spectrum of f < fcut for a > 0. These two effects are schematically described in the left panel of Figure 30.
A more quantitative explanation follows. From the relation of the luminosity of gravitational waves, the power spectrum of gravitational waves is written as
In the 1.5 PN approximation, dE/df in the inspiral phase is written as
where we write only the terms associated with the lowest-order spin-orbit coupling term assuming that the NS spin is zero, and omit other terms. Ŝ and \({{\bf{\hat L}}}\) are unit vectors of the BH spin and orbital angular momentum, respectively. Thus, for a given frequency f, |dE/df| is larger in the presence of the prograde spin (\(({\bf{\hat S}} \cdot {\bf{\hat L}} > 0)\)) than for a = 0. The binary evolves due to gravitational-wave emission, and hence, the binary with \({\bf{\hat S}} \cdot {\bf{\hat L}} > 0\) has to emit more gravitational waves than for a = 0 to increase the frequency (to decrease the orbital separation). This agrees with the explanation given above. In addition, Equation (129) shows that dE/df is proportional to the square of the effective amplitude \((f\tilde h(f))\). Therefore, the effective amplitude for a given frequency with Ŝ· > 0 should be larger than that for a = 0. This agrees completely with the numerical results.
For binaries composed of a high-spin BH, tidal disruption can occur outside the ISCO even for a high-mass BH for a variety of EOS. Thus, the dependence of fcut on the EOS is clearly seen even for a high value of Q. The right panel of Figure 29 shows the spectrum for Q = 4, MNS = 1.35 M⊙, and a = 0.75 with four different EOS. For all the EOS, tidal disruption occurs, and the value of fcut depends strongly on the EOS. For EOS 2H and H, the spectra are type-I, but for EOS HB and B (stiff EOS), they are type-III. Thus, for a high BH spin, a type-I or type-III spectrum is often seen even for a high value of Q.
With the increase of Q (for a canonical mass of a NS ∼ 1.4 M⊙), the value of fcut decreases (cf. Equation (7)), and the effective amplitude at f = fcut increases as the total mass increases. These are also favorable properties for gravitational-wave detection. The right panel of Figure 29 indeed illustrates that fcut is smaller than 2 kHz irrespective of the EOS, and also, that the effective amplitude at f ≲ 2 kHz is as large as the noise curve of the advanced detector for a hypothetical distance of D = 100 Mpc. For an even higher spin, say a ≳ 0.9, tidal disruption is likely to occur for a higher BH mass with Q ∼ 10. For such a case, the amplitude of gravitational waves at tidal disruption is likely to be high enough to be observable irrespective of EOS for D = 100 Mpc. This indicates that a BH-NS binary with a high BH spin will be a promising experimental field for constraining the EOS of high-density nuclear matter, when advanced gravitational-wave detectors are in operation.
3.8 Summary and issues for the near future
The inspiral and merger of BH-NS binaries are among promising sources for kilometer size laser-interferometric gravitational-waves detectors. The merger remnant is also a possible candidate for the progenitor of the central engine of SGRB. BH-NS binaries are also invaluable experimental fields for studying high-density nuclear matter through astronomical observations. To derive accurate gravitational waveforms in the late inspiral and merger phases, and to explore the compact-binary-merger hypothesis for the central engine of SGRB, the numerical simulation in full general relativity, taking into account realistic physics, is the unique approach. We review the progress and current status of numerical simulations for BH-NS binaries, and summarize the current understanding obtained from numerical results. The following is a summary as of June 2011:
-
In the final phase of BH-NS binaries, the NS is either tidally disrupted or swallowed by the companion BH. For a typical compactness of the NS, \({\mathcal C} = 0.14 - 0.20\), with zero BH spin, tidal disruption occurs outside the ISCO only for a small mass ratio of Q ≲ 3. For the case in which tidal disruption occurs, the final remnant is a BH surrounded by a disk of relatively small mass (say ≲ 0.1 M⊙).
-
The effects associated with BH spin enhance the possibilities for tidal disruption and for disk formation. Even for a moderately large spin a = 0.5, the criterion of tidal disruption for the mass ratio is relaxed to Q ≲ 5, for, e.g., \({\mathcal C} = 0.17\). In addition the effects of BH spin increase the mass of a remnant disk surrounding a BH to ∼ 0.1−0.3 M⊙ for a typical NS of mass MNS = 1.35 M⊙ with a = 0.75 and Q ∼ 5 [109]. For a favorable condition, such as \({\mathcal C} = 0.145\) and a = 0.9, the disk mass may be ≳ 0.5 M⊙ [74].
-
For a binary composed of a high-spin BH with high mass ratio, the disk, if it is formed, has a spread structure. However, the simulations so far (in which detailed microphysical effects such as neutrino wind are not taken into account) have not shown any evidence that a fraction of NS material escapes from the system.
-
The final merger process is well reflected in gravitational waveforms. Up to now, it has been found that there are at least three types of gravitational waveform. (i) For the case in which tidal disruption occurs far outside the ISCO, the amplitude of gravitational waves steeply damps in the middle of the late inspiral phase, and ringdown gravitational waves associated with a QNM of the remnant BH are not seen clearly. This type is referred to as type-I. For the case in which tidal disruption does not occur outside the ISCO, ringdown gravitational waves associated with a QNM of the remnant BH are clearly seen in the final phase of the gravitational-wave signal. This type is referred to as type-II. For the case in which tidal disruption occurs near the ISCO, there are two possibilities. One is that the amplitude of the gravitational waves steeply damps and the ringdown signal of a QNM is not seen clearly. This is the case that the mass ratio Q (and thus BH mass) is small, and the resulting type of the gravitational waveform is type-I. For a large value of Q (for a high BH mass), the disrupted material falls into the BH from a narrow region of the BH surface. In such cases, both the feature of steep damping associated with tidal disruption and ringdown gravitational waves associated with a QNM are seen. This type is referred to as type-III.
-
Reflecting that there are three types of gravitational waveforms, the gravitational-wave spectrum is also classified into three types. For type-I and type-III, the gravitational-wave spectrum is characterized by the cutoff frequency associated with tidal disruption. For a given set of masses of BH and NS, and BH spin, the cutoff frequency is determined by the EOS of the NS. Thus, if the cutoff frequencies are determined for a detected signal of gravitational waves, the EOS of the NS will be constrained. The cutoff frequency is higher than ∼ 1 kHz (e.g., Equation (8)). The frequency is lower for a NS of larger radii or for a rapidly spinning BH with a large BH mass. In particular, for a binary composed of a high-spin BH, the effective amplitude at f = fcut is enhanced by the spin-orbit coupling effect. This effect is favorable for detecting a gravitational-wave signal at the cutoff frequency by advanced detectors.
There are several issues to be solved for the near future. First, more realistic modeling of NS is required because numerical studies have been performed with quite simple EOS and microphysics up till now. For more realistic modeling of BH-NS binaries (in particular for modeling formation and evolution processes of a disk surrounding a BH), more physical EOS should be taken into account; we have to take into account finite-temperature EOS, neutrino process, and magnetic fields (accurately evolving magnetic field configurations). Second, there is still a wide range of the parameter space that has not been studied. In particular, binaries of high BH spin (a > 0.9) have not been studied yet. For the case in which BH spin is close to unity, the NS may be tidally disrupted even for a high mass ratio Q ∼ 20; cf. Equation (12). This possibility has not been explored yet. For such a high-mass binary, tidal disruption occurs at a relatively-low gravitational-wave frequency ∼ 1 kHz. This is favorable for observing the tidal-disruption event by gravitational-wave detectors, and thus, this deserves intense study. Recent work by Liu et al. [130] indicated it feasible to perform a simulation with a high spin a ∼ 0.99 using a simple prescription (see also [133]). A simulation with such a high spin will be done in a few years. Third, only one study has been done for the merger process of the binaries in which the BH spin and orbital angular momentum vectors misalign. In particular, any study of gravitational waveforms has not been done for this case. This is also an issue to be explored. Finally, it is necessary to optimize simulation codes to efficiently and accurately perform a large number of longterm simulations for a wide range of parameter space. This is required for preparing template sets of gravitational waves that are used for gravitational-wave data analysis. Work along this line has recently begun in 2010 [153, 110], and in the next several years, it will be encouraged because the preparation of theoretical templates is an urgent task for advanced gravitational-wave detectors.
References
Abadie, J. et al. (LIGO Scientific Collaboration), “Calibration of the LIGO Gravitational Wave Detectors in the Fifth Science Run”, Nucl. Instrum. Methods A, 624, 223–240, (2010). [DOI], [arXiv: 1007.3973]. (Cited on page 6.)
Abbott, B.P. et al. (LIGO Scientific Collaboration), “LIGO: the Laser Interferometer Gravitational-Wave Observatory”, Rep. Prog. Phys., 72, 076901, (2009). [DOI]. (Cited on pages 6 and 66.)
Accadia, T. et al. (Virgo Collaboration), “Calibration and sensitivity of the Virgo dector during its second science run”, Class. Quantum Grav., 28, 025005, (2011). [DOI], [arXiv:1009.5190]. (Cited on page 6.)
Acernese, F. et al. (Virgo Collaboration), “Status of VIRGO”, Class. Quantum Grav., 25, 114045, (2008). [DOI]. (Cited on page 6.)
Ajith, P. et al., “Template bank for gravitational waveforms from coalescing binary black holes: Nonspinning binaries”, Phys. Rev. D, 77, 104017, (2008). [DOI], [arXiv:0710.2335]. (Cited on pages 60 and 65.)
Anderson, M., Hirschmann, E.W., Lehner, L., Liebling, S.L., Motl, P.M., Neilsen, D., Palenzuela, C. and Tohline, J.E., “Simulating binary neutron stars: Dynamics and gravitational waves”, Phys. Rev. D, 77, 024006, (2008). [DOI], [ADS]. (Cited on pages 39 and 74.)
Anderson, M., Hirschmann, E.W., Liebling, S.L. and Neilsen, D., “Relativistic MHD with adaptive mesh refinement”, Class. Quantum Grav., 23, 6503–6524, (2006). [DOI]. (Cited on page 44.)
Ansorg, M., “A multi-domain spectral method for initial data of arbitrary binaries in general relativity”, Class. Quantum Grav., 24, S1–S14, (2007). [DOI], [ADS]. (Cited on page 11.)
Asada, H., “Formulation for the internal motion of quasiequilibrium configurations in general relativity”, Phys. Rev. D, 57, 7292–7298, (1998). [DOI]. (Cited on page 22.)
Ashtekar, A. and Krishnan, B., “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, lrr-2004-10, (2004). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2004-10. (Cited on pages 17 and 20.)
Baiotti, L., Damour, T., Giacomazzo, B., Nagar, A. and Rezzolla, L., “Analytic modelling of tidal effects in the relativistic inspiral of binary neutron stars”, arXiv, e-print, (2010). [arXiv: 1009.0521 [gr-qc]]. (Cited on pages 6 and 40.)
Baiotti, L., Damour, T., Giacomazzo, B., Nagar, A. and Rezzolla, L., “Accurate numerical simulations of inspiralling binary neutron stars and their comparison with effective-one-body analytical models”, arXiv, e-print, (2011). [arXiv:1103.3874 [gr-qc]]. (Cited on pages 6 and 40.)
Baiotti, L., Giacomazzo, B. and Rezzolla, L., “Accurate evolutions of inspiraling neutron-star binaries: Prompt and delayed collapse to a black hole”, Phys. Rev. D, 78, 084033, (2008). [DOI], [arXiv:0804.0594]. (Cited on page 40.)
Baiotti, L., Shibata, M. and Yamamoto, T., “Binary neutron-star mergers with Whisly and SACRA: First quantitative comparison of results from independent general-relativistic hydrodynamics codes”, Phys. Rev. D, 82, 064015, (2010). [DOI]. (Cited on pages 40 and 44.)
Baker, J.G., Centrella, J., Choi, D.-I., Koppitz, M. and van Meter, J., “Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes”, Phys. Rev. Lett., 96, 111102, (2006). [DOI]. (Cited on pages 20 and 39.)
Bardeen, J.M., Press, W.H. and Teukolsky, S.A., “Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation”, Astrophys. J., 178, 347–369, (1972). [DOI], [ADS]. (Cited on pages 8 and 49.)
Baumgarte, T.W., Ó Murchadha, N. and Pfeiffer, H.P., “Einstein constraints: uniqueness and nonuniqueness in the conformal thin sandwich approach”, Phys. Rev. D, 75, 044009, (2007). [DOI]. (Cited on page 19.)
Baumgarte, T.W. and Shapiro, S.L., “Numerical integration of Einstein’s field equation”, Phys. Rev. D, 59, 024007, (1998). [DOI], [ADS], [gr-qc/9810065]. (Cited on page 39.)
Baumgarte, T.W., Skoge, M.L. and Shapiro, S.L., “Black hole-neutron star binaries in general relativity: quasiequilibrium formulation”, Phys. Rev. D, 70, 064040, (2004). [DOI]. (Cited on page 10.)
Belczynski, K., Taam, R.E., Kalogera, V., Rasio, F.A. and Bulik, T., “On the rarity of double black hole binaries: consequences for gravitational wave detection”, Astrophys. J., 662, 504, (2007). [DOI]. (Cited on page 5.)
Belczynski, K., Taam, R.E., Rantsiou, E. and van der Sluys, M., “Black hole spin evolution: implications on short-hard gamma-ray bursts and gravitational wave detection”, Astrophys. J., 682, 474, (2008). [DOI]. (Cited on page 5.)
Benz, W., Bowers, R.L., Cameron, A.G.W. and Press, W.H., “Dynamic mass exchange in doubly degenerate binaries”, Astrophys. J., 348, 647, (1990). [DOI]. (Cited on page 12.)
Berger, M. and Oliger, J., “Adaptive Mesh Refinement for Hyperbolic Partial Differential Equations”, J. Comput. Phys., 53, 484, (1984). [DOI]. (Cited on page 44.)
Bildsten, L. and Cutler, C., “Tidal interactions of inspiraling compact binaries”, Astrophys. J., 400, 175–180, (1992). [DOI]. (Cited on page 45.)
Blanchet, L., “Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries”, Living Rev. Relativity, 9, lrr-2006-4, (2006). [gr-qc/0202016]. URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2006-4. (Cited on pages 5, 7, 29, 30, 31, 39, and 60.)
Bonazzola, S., Gourgoulhon, E. and Marck, J.-A., “Relativistic formalism to compute quasiequilibrium configurations of nonsynchronized neutron star binaries”, Phys. Rev. D, 56, 7740–7749, (1997). [DOI]. (Cited on page 22.)
Bonazzola, S., Gourgoulhon, E. and Marck, J.-A., “Numerical approach for high presicion 3D relativistic star models”, Phys. Rev. D, 58, 104020, (1998). [DOI], [ADS]. (Cited on page 11.)
Bonazzola, S., Gourgoulhon, E. and Marck, J.-A., “Spectral methods in general astrophysics”, J. Comput. Appl. Math., 109, 433–473, (1999). [DOI], [ADS]. (Cited on page 11.)
Bowen, J.M. and York Jr, J.W., “Time-asymmetric initial data for black holes and black-hole collisions”, Phys. Rev. D, 21, 2047–2056, (1980). [DOI]. (Cited on page 17.)
Boyle, M., Brown, D.A., Kidder, L.E., Mroué, A.H., Pfeiffer, H.P., Scheel, M.A., Cook, G.B. and Teukolsky, S.A., “High-accuracy comparison of numerical relativity simulations with post-Newtonian expansions”, Phys. Rev. D, 76, 124038, (2007). [DOI], [arXiv:0710.0158]. (Cited on pages 15 and 60.)
Boyle, M., Buonanno, A., Kidder, L.E., Mroué, A.H., Pan, Y., Pfeiffer, H.P. and Scheel, M.A., “High-accuracy numerical simulation of black-hole binaries: computation of gravitational-wave energy flux and comparisons with post-Newtonian approximants”, Phys. Rev. D, 78, 104020, (2008). [DOI]. (Cited on pages 15 and 60.)
Brandt, S. and Brügmann, B., “A simple construction of initial data for multiple black holes”, Phys. Rev. Lett., 78, 3606–3609, (1997). [DOI]. (Cited on pages 17, 20, and 39.)
Brill, D.R. and Lindquist, R.W., “Interaction Energy in Geometrostatics”, Phys. Rev., 131, 471–476, (1963). [DOI], [ADS]. (Cited on page 20.)
Brown, D., Sarbach, O., Schnetter, E., Tiglio, M., Diener, P., Hawke, I. and Pollney, D., “Excision without excision”, Phys. Rev. D, 76, 081503, (2007). [DOI]. (Cited on page 37.)
Brügmann, B., González, J.A., Hannam, M., Husa, S., Sperhake, U. and Tichy, W., “Calibration of moving puncture simulations”, Phys. Rev. D, 77, 024027, (2008). (Cited on pages 39 and 44.)
Buonanno, A., Cook, G.B. and Pretorius, F., “Inspiral, merger, and ring-down of equal-mass black-hole binaries”, Phys. Rev. D, 75, 124018, (2007). [DOI]. (Cited on pages 60 and 66.)
Buonanno, A. and Damour, T., “Effective one-body approach to general relativistic two-body dynamics”, Phys. Rev. D, 59, 084006, (1999). [DOI], [gr-qc/9811091]. (Cited on page 6.)
Cameron, A.G.W. and Iben Jr, I., “On the behavior of double degenerate binaries associated with Type I supernovae”, Astrophys. J., 305, 228, (1986). [DOI]. (Cited on page 12.)
Campanelli, M., Lousto, C.O., Marronetti, P. and Zlochower, Y., “Accurate evolutions of orbiting black-hole binaries without excision”, Phys. Rev. Lett., 96, 111101, (2006). [DOI], [ADS]. (Cited on pages 20 and 39.)
Caudill, M., Cook, G.B., Grigsby, J.D. and Pfeiffer, H.P., “Circular orbits and spin in black-hole initial data”, Phys. Rev. D, 74, 064011, (2006). [DOI], [ADS]. (Cited on pages 11, 20, and 33.)
Chawla, S., Anderson, M., Besselman, M., Lehner, L., Liebling, S.L., Motl, P.M. and Neilsen, D., “Mergers of Magnetized Neutron Stars with Spinning Black Holes: Disruption, Accretion and Fallback”, Phys. Rev. Lett., 105, 111101, (2010). [DOI]. (Cited on pages 15, 38, 45, 46, and 53.)
Christodoulou, D., “Reversible and irreversible transformations in black-hole physics”, Phys. Rev. Lett., 25, 1596, (1970). [DOI]. (Cited on pages 26 and 27.)
Clark, J.P.A. and Eardley, D.M., “Evolution of close neutron star binaries”, Astrophys. J., 215, 311–322, (1977). [DOI]. (Cited on pages 12 and 14.)
Cook, G.B., “Initial Data for Numerical Relativity”, Living Rev. Relativity, 3, lrr-2000-5, (2000). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2000-5. (Cited on page 17.)
Cook, G.B., “Corotating and irrotational binary black holes in quasicircular orbits”, Phys. Rev. D, 65, 084003, (2002). [DOI], [ADS]. (Cited on page 20.)
Cook, G.B. and Baumgarte, T.W., “Excision boundary conditions for the conformal metric”, Phys. Rev. D, 78, 104016, (2008). [DOI]. (Cited on page 36.)
Cook, G.B. and Pfeiffer, H.P., “Excision boundary conditions for black hole initial data”, Phys. Rev. D, 70, 104016, (2004). [DOI], [ADS]. (Cited on pages 11, 17, and 20.)
Cook, G.B. and Whiting, B.F., “Approximate Killing vectors on S2”, Phys. Rev. D, 76, 041501, (2007). [DOI], [arXiv:0706.0199]. (Cited on page 20.)
Cutler, C. and Flanagan, É.É., “Gravitational waves from merging compact binaries: How accurately can one extract the binary’s parameters from the inspiral waveform?”, Phys. Rev. D, 49, 2658–2697, (1994). [DOI], [gr-qc/9402014]. (Cited on page 9.)
Damour, T. and Nagar, A., “Effective one body description of tidal effects in inspiralling compact binaries”, Phys. Rev. D, 81, 084016, (2010). [DOI]. (Cited on pages 6 and 10.)
Demorest, P.B., Pennucci, T., Ransom, S.M., Roberts, M.S.E. and Hessels, J.W.T., “Shapiro delay measurement of a two solar mass neutron star”, Nature, 467, 1081, (2010). [DOI]. (Cited on pages 41 and 43.)
Dimmelmeier, H., Novak, J., Font, J.A., Ibáñez, J.M. and Müller, E., “Combining spectral and shock-capturing methods: A new numerical approach for 3D relativistic core collapse simulations”, Phys. Rev. D, 71, 064023, (2005). [DOI], [ADS], [arXiv:astro-ph/0407174]. (Cited on page 44.)
Dimmelmeier, H., Ott, C.D., Janka, H.-T., Marek, A. and Müller, E., “Generic gravitational-wave signals from the collapse of rotating stellar cores”, Phys. Rev. Lett., 98, 251101, (2007). [DOI], [ADS], [arXiv:astro-ph/0702305]. (Cited on page 43.)
Dimmelmeier, H., Ott, C.D., Marek, A. and Janka, H.-T., “Gravitational wave burst signal from the core collapse of rotating stars”, Phys. Rev. D, 78, 064056, (2008). [DOI], [ADS], [arXiv:0806.4953]. (Cited on page 43.)
Dreyer, O., Krishnan, B., Shoemaker, D. and Schnetter, E., “Introduction to isolated horizon in numerical relativity”, Phys. Rev. D, 67, 024018, (2003). [DOI]. (Cited on page 20.)
Duez, M.D., “Numerical relativity confronts compact neutron star binaries: a review and status report”, Class. Quantum Grav., 27, 114002, (2010). [DOI]. (Cited on page 15.)
Duez, M.D., Foucart, F., Kidder, L.E., Ott, C.D. and Teukolsky, S.A., “Equation of state effects in black hole-neutron star mergers”, Class. Quantum Grav., 27, 114106, (2010). [DOI]. (Cited on pages 11, 12, 15, 38, 43, 46, 50, 53, 54, and 58.)
Duez, M.D., Foucart, F., Kidder, L.E., Pfeiffer, H.P., Scheel, M.A. and Teukolsky, S.A., “Evolving black hole-neutron star binaries in general relativity using pseudospectral and finite difference methods”, Phys. Rev. D, 78, 104015, (2008). [DOI]. (Cited on pages 11, 15, 38, 44, 60, and 74.)
Duez, M.D., Marronetti, P., Shapiro, S.L. and Baumgarte, T.W., “Hydrodynamic simulations in 3+1 general relativity”, Phys. Rev. D, 67, 024004, (2003). [DOI]. (Cited on page 15.)
Eggleton, P.P., “Approximations to the radii of Roche lobes”, Astrophys. J., 268, 368–369, (1983). [DOI]. (Cited on page 32.)
Etienne, Z.B., Faber, J.A., Liu, Y.T., Shapiro, S.L. and Baumgarte, T.W., “Filling the holes: evolving excised binary black hole initial data with puncture techniques”, Phys. Rev. D, 76, 101503, (2007). [DOI]. (Cited on page 37.)
Etienne, Z.B., Faber, J.A., Liu, Y.T., Shapiro, S.L., Taniguchi, K. and Baumgarte, T.W., “Fully general relativistic simulations of black hole-neutron star mergers”, Phys. Rev. D, 77, 084002, (2008). [DOI], [arXiv:0712.2460]. (Cited on pages 15, 38, and 58.)
Etienne, Z.B., Liu, Y.T., Shapiro, S.L. and Baumgarte, T.W., “Relativistic simulations of black hole-neutron star mergers: effects of black hole spin”, Phys. Rev. D, 79, 044024, (2009). [DOI]. (Cited on pages 15, 38, 46, 49, 50, 55, 56, 57, 58, 60, 64, and 65.)
Faber, J.A., Baumgarte, T.W., Shapiro, S.L. and Taniguchi, K., “General Relativistic Binary Merger Simulations and Short Gamma-Ray Bursts”, Astrophys. J. Lett., 641, L93–L96, (2006). [DOI]. (Cited on page 11.)
Faber, J.A., Baumgarte, T.W., Shapiro, S.L., Taniguchi, K. and Rasio, F., “Dynamical evolution of black hole-neutron star binaries in general relativity: Simulations of tidal disruption”, Phys. Rev. D, 73, 024012, (2006). [DOI], [ADS]. (Cited on page 11.)
Faber, J.A. and Rasio, F., “Post-Newtonian SPH calculations of binary neutron star coalescence: Method and first results”, Phys. Rev. D, 62, 064012, (2000). [DOI]. (Cited on page 8.)
Faber, J.A. and Rasio, F., “Post-Newtonian SPH calculations of binary neutron star coalescence. III. Irrotational systems and gravitational wave spectra”, Phys. Rev. D, 65, 084042, (2002). [DOI]. (Cited on page 8.)
Faber, J.A., Rasio, F. and Manor, J.B., “Post-Newtonian smoothed particle hydrodynamics calculations of binary neutron star coalescence. II. Binary mass ratio, equation of state, and spin dependence”, Phys. Rev. D, 63, 044012, (2001). [DOI]. (Cited on page 8.)
Ferrari, V., Gualtieri, L. and Pannarale, F., “A semi-relativistic model for tidal interactions in BH-NS coalescing binaries”, Class. Quantum Grav., 26, 125004, (2009). [DOI]. (Cited on page 8.)
Ferrari, V., Gualtieri, L. and Pannarale, F., “Neutron star tidal disruption in mixed binaries: The imprint of the equation of state”, Phys. Rev. D, 81, 064026, (2010). [DOI]. (Cited on pages 8, 9, and 41.)
Fishbone, L.G., “The Relativistic Roche Problem. I. Equilibrium Theory for a Body in Equatorial, Circular Orbit around a Kerr Black Hole”, Astrophys. J., 185, 43, (1973). [DOI]. (Cited on pages 8 and 10.)
Flanagan, É.É. and Hinderer, T., “Constraining neutron star tidal Love numbers with gravitational wave detectors”, Phys. Rev. D, 77, 021502, (2008). [DOI]. (Cited on page 8.)
Font, J.A., “Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity”, Living Rev. Relativity, 11, lrr-2008-7, (2008). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2008-7. (Cited on page 40.)
Foucart, F., Duez, M.D., Kidder, L.E. and Teukolsky, S.A., “Black hole-neutron star mergers: Effects of the orientation of the black hole spin”, Phys. Rev. D, 83, 024005, (2010). [DOI]. (Cited on pages 11, 15, 38, 43, 50, 52, 55, 56, 57, and 71.)
Foucart, F., Kidder, L.E., Pfeiffer, H.P. and Teukolsky, S.A., “Initial data for black hole-neutron star binaries: a flexible, high-accuracy spectral method”, Phys. Rev. D, 77, 124051, (2008). [DOI]. (Cited on pages 11, 19, 29, and 37.)
Friedman, J.L., Uryū, K. and Shibata, M., “Thermodynamics of binary black holes and neutron stars”, Phys. Rev. D, 65, 064035, (2002). [DOI]. (Cited on page 27.)
Garfinkle, D., “Harmonic coordinate method for simulating generic singularities”, Phys. Rev. D, 65, 044029, (2002). [DOI], [ADS]. (Cited on page 39.)
Gourgoulhon, E., Grandclément, P. and Bonazzola, S., “Binary black holes in circular orbits. I. A global spacetime approach”, Phys. Rev. D, 65, 044020, (2002). [DOI], [ADS]. (Cited on page 17.)
Gourgoulhon, E., Grandclément, P., Marck, J.-A. and Novak, J., “LORENE: Langage Objet pour la RElativité NumériquE”, project homepage, L’Observatoire de Paris. URL (accessed 20 December 2010): http://www.lorene.obspm.fr. (Cited on page 11.)
Gourgoulhon, E., Grandclément, P., Taniguchi, K., Marck, J.-A. and Bonazzola, S., “Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. Methods and tests”, Phys. Rev. D, 63, 064029, (2001). [DOI], [ADS]. (Cited on pages 17, 22, 23, and 28.)
Gourgoulhon, E. and Jaramillo, J.L., “A 3+1 perspective on null hypersurfaces and isolated horizons”, Phys. Rep., 423, 159–294, (2006). [DOI], [ADS]. (Cited on pages 17 and 20.)
Grandclément, P., “Accurate and realistic initial data for black hole-neutron star binaries”, Phys. Rev. D, 74, 124002, (2006). [DOI], [ADS]. (Cited on pages 10, 25, 29, and 37.)
Grandclément, P., “Erratum: Accurate and realistic initial data for black hole-neutron star binaries [Phys. Rev. D 74, 124002 (2006)]”, Phys. Rev. D, 75, 129903(E), (2007). [DOI]. (Cited on pages 10, 25, 29, and 37.)
Grandclément, P., Bonazzola, S., Gourgoulhon, E. and Marck, J.-A., “A multidomain spectral method for scalar and vectorial poisson equations with noncompact sources”, J. Comput. Phys., 170, 231–260, (2001). [DOI], [ADS]. (Cited on page 11.)
Grandclément, P. and Novak, J., “Spectral Methods for Numerical Relativity”, Living Rev. Relativity, 12, lrr-2009-1, (2009). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2009-1. (Cited on page 11.)
Gundlach, C., Calabrese, G., Hinder, I. and Martín-García, J.M., “Constraint damping in the Z4 formulation and harmonic gauge”, Class. Quantum Grav., 22, 3767–3773, (2005). [DOI], [ADS]. (Cited on page 39.)
Haensel, P. and Potekhin, A.Y., “Analytical representations of unified equations of state of neutron-star matter”, Astron. Astrophys., 428, 191, (2004). [DOI]. (Cited on page 42.)
Hannam, M., Husa, S., Brügmann, B. and Ó Murchadha, N., “Geometry and Regularity of Moving Punctures”, Phys. Rev. Lett., 99, 241102, (2007). [DOI]. (Cited on page 39.)
Harten, A., Lax, P.D. and van Leer, B., “On upstream differencing and Godunov-type schemes for hyperbolic conservation laws”, SIAM Rev., 25, 35–61, (1983). [DOI]. (Cited on page 40.)
Hawley, J.F., “Three-dimensional simulations of black hole tori”, Astrophys. J., 381, 496–507, (1991). [DOI], [ADS]. (Cited on page 46.)
Hild, S., Chelkowski, S. and Freise, A., “Pushing towards the ET sensitivity using ‘conventional’ technology”, arXiv, e-print, (2008). [arXiv:0810.0604 [gr-qc]]. (Cited on pages 6, 66, and 68.)
Hild, S. et al., “Sensitivity Studies for Third-Generation Gravitational Wave Observatories”, arXiv, e-print, (2010). [arXiv:1012.0908 [gr-qc]]. (Cited on pages 6, 66, and 68.)
Imbirba, B., Baker, J., Choi, D.-I., Centrella, J., Fiske, D.F., Brown, D. and van Meter, J.R., “Evolving a puncture black hole with fixed mesh refinement”, Phys. Rev. D, 70, 124025, (2004). [DOI]. (Cited on page 44.)
Ishii, M., Shibata, M. and Mino, Y., “Black hole tidal problem in the Fermi normal coordniates”, Phys. Rev. D, 71, 044017, (2005). [DOI]. (Cited on pages 8, 9, 10, and 32.)
Janka, H.-T., Eberl, T., Ruffert, M. and Fryer, C.L., “Black Hole-Neutron Star Mergers as Central Engines of Gamma-Ray Bursts”, Astrophys. J. Lett., 527, L39, (1999). [DOI]. (Cited on pages 11, 12, 14, and 54.)
Jaranowski, P. and Królak, A., “Gravitational-Wave Data Analysis. Formalism and Sample Applications: The Gaussian Case”, Living Rev. Relativity, 8, lrr-2005-3, (2005). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2005-3. (Cited on page 9.)
Kalogera, V., Belczynski, K., Kim, C., O’Shaughnessy, R. and Willems, B., “Formation of double compact objects”, Phys. Rep., 442, 75, (2007). [DOI]. (Cited on page 5.)
Kalogera, V. et al., “The Cosmic Coalescence Rates for Double Neutron Star Binaries”, Astrophys. J. Lett., 601, L179–L182, (2004). [DOI]. (Cited on page 5.)
Kaspi, V.M., Roberts, M.S.E. and Harding, A.K., “Isolated neutron stars”, in Lewin, W.H.G. and van der Klis, M., eds., Compact Stellar X-ray Sources, Cambridge Astrophysics Series, 39, pp. 279–340, (Cambridge University Press, Cambridge, 2006). [Google Books]. (Cited on page 41.)
Kidder, L.E., “Coalescing binary systems of compact objects to (post)5/2-Newtonian order. V. Spin effects”, Phys. Rev. D, 52, 821–847, (1995). [DOI], [ADS]. (Cited on page 49.)
Kidder, L.E., “Using full information when computing modes of post-Newtonian waveforms from inspiraling compact binaries in circular orbit”, Phys. Rev. D, 77, 044016, (2008). [DOI], [arXiv:0710.0614]. (Cited on page 60.)
Kidder, L.E., Will, C.M. and Wiseman, A.G., “Spin effects in the inspiral of coalescing compact binaries”, Phys. Rev. D, 47, R4183–R4187, (1993). [DOI]. (Cited on page 49.)
Kiuchi, K., Shibata, M., Montero, P.J. and Font, J.A., “Gravitational waves from the Papaloizou-Pringle instability in black hole-torus systems”, Phys. Rev. Lett., 106, 251102, (2011). [DOI], [arXiv:1105.5035]. (Cited on page 46.)
Kochanek, C.S., “Coalescing Binary Neutron Stars”, Astrophys. J., 398, 234–247, (1992). [DOI]. (Cited on page 45.)
Kurganov, A. and Tadmor, E., “New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations”, J. Comput. Phys., 160, 241–282, (2000). [DOI]. (Cited on page 40.)
Kyutoku, K., Shibata, M. and Taniguchi, K., “Quasiequilibrium states of black hole-neutron star binaries in moving-puncture framework”, Phys. Rev. D, 79, 124018, (2009). [DOI]. (Cited on pages 11, 17, 21, 25, 29, and 37.)
Kyutoku, K., Shibata, M. and Taniguchi, K., “Gravitational waves from nonspinning black hole-neutron star binaries: Dependence on equations of state”, Phys. Rev. D, 82, 044049, (2010). [DOI], [1008.1460 [astro-ph.HE]]. (Cited on pages 9, 15, 38, 41, 42, 43, 45, 46, 47, 54, 55, 57, 60, 61, 66, 67, and 68.)
Kyutoku, K., Shibata, M. and Taniguchi, K., “Erratum: Gravitational waves from nonspinning black hole-neutron star binaries: Dependence on equations of state [Phys. Rev. D 82, 044049 (2010)]”, arXiv, e-print, (2011). [arXiv:1008.1460v3 [astro-ph.HE]]. (Cited on pages 15, 55, and 57.)
Kyutoku, K., Shibata, M. and Taniguchi, K., “Gravitational waves from spinning black holeneutron star binaries: Dependence on black hole spins and on neutron star equations of state”, Phys. Rev. D, accepted, (2011). [arXiv:1108.1189]. (Cited on pages 9, 15, 38, 42, 45, 46, 50, 51, 52, 53, 54, 55, 56, 57, 60, 63, 67, 69, and 71.)
Lackey, B.D., Kyutoku, K., Shibata, M. and Brady, P.R. abd Friedman, J.L., “Extracting equation of state parameters from black hole-neutron star mergers. I. Nonspinning black holes”, Phys. Rev. D, in preparation, (2011). (Cited on page 72.)
Lai, D., Rasio, F.A. and Shapiro, S.L., “Ellipsoidal figures of equilibrium: compressible models”, Astrophys. J. Suppl. Ser., 88, 205–252, (1993). [DOI]. (Cited on pages 7 and 10.)
Lai, D., Rasio, F.A. and Shapiro, S.L., “Equilibrium, stability, and orbital evolution of close binary systems”, Astrophys. J., 423, 344, (1994). [DOI]. (Cited on page 7.)
Lai, D., Rasio, F.A. and Shapiro, S.L., “Hydrodynamic instability and coalescence of binary neutron stars”, Astrophys. J., 420, 811, (1994). [DOI]. (Cited on page 7.)
Lai, D. and Wiseman, A.G., “Innermost stable circular orbit of inspiraling neutron-star binaries: Tidal effects, post-Newtonian effects, and the neutron-star equation of state”, Phys. Rev. D, 54, 3958, (1996). [DOI]. (Cited on pages 8 and 10.)
Lattimer, J.M. and Prakash, M., “Neutron star structure and the equation of state”, Astrophys. J., 550, 426–442, (2001). [DOI], [ADS]. (Cited on pages 7 and 41.)
Lattimer, J.M. and Prakash, M., “The Physics of Neutron Stars”, Science, 304, 536–542, (2004). [DOI], [astro-ph/0405262]. (Cited on pages 7, 12, and 41.)
Lattimer, J.M. and Prakash, M., “Neutron star observations: Prognosis for equation of state constraints”, Phys. Rep., 442, 109–165, (2007). [DOI], [astro-ph/0612440]. (Cited on page 41.)
Lattimer, J.M. and Schramm, D.N., “Black-hole-neutron-star collisions”, Astrophys. J. Lett., 192, L145, (1974). [DOI]. (Cited on page 10.)
Lattimer, J.M. and Swesty, D.F., “A generalized equation of state for hot, dense matter”, Nucl. Phys. A, 535, 331–376, (1991). [DOI]. (Cited on page 43.)
“LCGT: Large-scale Cryogenic Gravitational wave Telescope”, project homepage, ICRR. URL (accessed 20 December 2010): http://gw.icrr.u-tokyo.ac.jp/lcgt/. (Cited on page 6.)
Lee, W.H., “Newtonian hydrodynamics of the coalescence of black holes with neutron stars — III. Irrotational binaries with a stiff equation of state”, Mon. Not. R. Astron. Soc., 318, 606, (2000). [DOI]. (Cited on page 11.)
Lee, W.H., “Newtonian hydrodynamics of the coalescence of black holes with neutron stars — IV. Irrotational binaries with a soft equation of state”, Mon. Not. R. Astron. Soc., 328, 583, (2001). [DOI]. (Cited on page 11.)
Lee, W.H. and Kluźniak, W., “Newtonian hydrodynamics of the coalescence of black holes with neutron stars — II. Tidally locked binaries with a soft equation of state”, Mon. Not. R. Astron. Soc., 308, 780, (1999). [DOI]. (Cited on page 11.)
Lee, W.H. and Kluźniak, W., “Newtonian Hydrodynamics of the Coalescence of Black Holes with Neutron Stars. I. Tidally Locked Binaries with a Stiff Equation of State”, Astrophys. J. Lett., 526, L178, (1999). [DOI]. (Cited on page 11.)
Lee, W.H., Ramirez-Ruiz, E. and van de Ven, G., “Short gamma-ray bursts from dynamically assembled compact binaries in globular clusters: Pathways, rates, hydrodynamics, and cosmological setting”, Astrophys. J., 720, 953, (2010). [DOI]. (Cited on page 5.)
“LIGO Laboratory Home Page”, project homepage, California Institute of Technology. URL (accessed 20 December 2010): http://www.ligo.caltech.edu/. (Cited on page 6.)
Lindblom, L., “Determining the nuclear equation of state from neutron-star masses and radii”, Astrophys. J., 398, 569, (1992). [DOI]. (Cited on pages 9 and 41.)
Lindblom, L., “Spectral representations of neutron-star equations of state”, Phys. Rev. D, 82, 103011, (2010). [DOI]. (Cited on page 42.)
Lindblom, L., Scheel, M.A., Kidder, L.E., Owen, R. and Rinne, O., “A new generalized harmonic evolution system”, Class. Quantum Grav., 23, S447–S462, (2006). [DOI], [ADS]. (Cited on pages 39 and 74.)
Liu, Y.T., Etienne, Z.B. and Shapiro, S.L., “Evolution of near-extremal-spin black holes using the moving puncture technique”, Phys. Rev. D, 80, 121503(R), (2010). (Cited on page 72.)
Lorimer, D.R., “Binary and Millisecond Pulsars”, Living Rev. Relativity, 11, lrr-2008-8, (2008). URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2008-8. (Cited on page 5.)
Lovelace, G., Owen, R., Pfeiffer, H.P. and Chu, T., “Binary-black-hole initial data with nearly extremal spins”, Phys. Rev. D, 78, 084017, (2008). [DOI], [ADS], [arXiv:0805.4192]. (Cited on pages 19 and 20.)
Lovelace, G., Scheel, M.A. and Szilágyi, B., “Simulating merging binary black holes with nearly extremal spins”, Phys. Rev. D, 83, 024010, (2010). [DOI], [1010.2777 [gr-qc]]. (Cited on page 72.)
Manasse, F.K. and Misner, C.W., “Fermi Normal Coordinates and Some Basic Concepts in Differential Geometry”, J. Math. Phys., 4, 735–745, (1963). [DOI]. (Cited on page 8.)
Marck, J.-A., “Solution to the Equations of Parallel Transport in Kerr Geometry; Tidal Tensor”, Proc. R. Soc. London, Ser. A, 385, 431, (1983). [DOI]. (Cited on page 8.)
Marronetti, P., Tichy, W., Brügmann, B., González, J.A. and Sperhake, U., “High-spin binary black hole mergers”, Phys. Rev. D, 77, 064010, (2008). [DOI], [arXiv:arXiv:0709.2160]. (Cited on page 39.)
Mashhoon, B., “On tidal phenomena in a strong gravitational field”, Astrophys. J., 197, 705, (1975). [DOI]. (Cited on page 8.)
Miller, M., “General Relativistic Initial Data for the Binary Black Hole / Neutron Star System in Quasicircular Orbit”, arXiv, e-print, (2001). [arXiv:gr-qc/0106017]. (Cited on page 10.)
Nakamura, T. and Oohara, K., “Gravitational radiation emitted by N particles in circular orbits”, Phys. Lett. A, 98, 483, (1983). [DOI]. (Cited on page 62.)
Nakamura, T., Oohara, K. and Kojima, Y., “General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes”, Prog. Theor. Phys. Suppl., 90, 1–218, (1987). [DOI]. (Cited on page 39.)
Nakamura, T. and Sasaki, M., “Is collapse of a deformed star always effectual for gravitational radiation?”, Phys. Lett. B, 106, 69–72, (1981). [DOI]. (Cited on page 62.)
Nakar, E., “Short-hard gamma-ray bursts”, Phys. Rep., 442, 166, (2007). [DOI]. (Cited on pages 6, 9, 10, and 53.)
Narayan, R., Paczyński, B. and Piran, T., “Gamma-Ray Bursts as the Death Throes of Massive Binary Stars”, Astrophys. J. Lett., 395, L83–L86, (1992). [DOI], [ADS]. (Cited on page 9.)
Narayan, R., Piran, T. and Shemi, A., “Neutron star and black hole binaries in the Galaxy”, Astrophys. J. Lett., 379, L17–L20, (1991). [DOI], [ADS]. (Cited on page 5.)
Ó Murchadha, N. and York Jr, J.W., “Initial-value problem of general relativity. I. General formulation and physical interpretation”, Phys. Rev. D, 10, 428–436, (1974). (Cited on page 18.)
Oechslin, R., Janka, H.-T. and Marek, A., “Relativistic neutron star merger simulations with non-zero temperature equations of state. I. Variation of binary parameters and equation of state”, Astron. Astrophys., 467, 395–409, (2007). [DOI]. (Cited on pages 40 and 43.)
O’Shaughnessy, R., Kalogera, V. and Belczynski, K., “Binary compact object coalescence rates: the role of elliptical galaxies”, Astrophys. J., 715, 1453, (2010). [DOI]. (Cited on page 5.)
O’Shaughnessy, R., Kim, C., Kalogera, V. and Belczynski, K., “Constraining Population Synthesis Models via Empirical Binary Compact Object Merger and Supernova Rates”, Astrophys. J., 672, 479–488, (2008). [DOI]. (Cited on page 5.)
Ott, C.D. et al., “Dynamics and Gravitational Wave Signature of Collapsar Formation”, Phys. Rev. Lett., 106, 161103, (2011). [DOI], [arXiv: 1012.1853 [astro-ph.HE]]. (Cited on page 43.)
Özel, F. and Psaltis, D., “Reconstructing the neutron-star equation of state from astrophysical measurements”, Phys. Rev. D, 80, 103003, (2009). [DOI], [arXiv:0905.1959]. (Cited on pages 42 and 45.)
Paczyński, B., “Evolutionary process in close binary systems”, Annu. Rev. Astron. Astrophys., 9, 183, (1971). [DOI]. (Cited on page 32.)
Paczyński, B. and Wiita, P.J., “Thick accretion disks and supercritical luminosities”, Astron. Astrophys., 88, 23–31, (1980). [ADS]. (Cited on page 11.)
Pannarale, F., Rezzolla, L., Ohme, F. and Read, J.S., “Will black hole-neutron star binary inspirals tell us about the neutron star equation of state?”, arXiv, e-print, (2011). [arXiv:1103.3526]. (Cited on page 72.)
Pannarale, F., Tonita, A. and Rezzolla, L., “Black hole-neutron star mergers and short GRBs: a relativistic toy model to estimate the mass of the torus”, Astrophys. J., 95, (2010). [DOI], [1007.4160 [astro-ph.HE]]. (Cited on pages 8, 15, 38, 45, 56, and 58.)
Peters, P.C., “Gravitational Radiation and the Motion of Two Point Masses”, Phys. Rev., 136, B1224–B1232, (1964). [DOI]. (Cited on page 5.)
Peters, P.C. and Mathews, J., “Gravitational radiation from point masses in a Keplerian orbit”, Phys. Rev., 131, 435–440, (1963). [DOI]. (Cited on page 5.)
Pfeiffer, H.P., Brown, D.A., Kidder, L.E., Lindblom, L., Lovelace, G. and Scheel, M.A., “Reducing orbital eccentricity in binary black hole simulations”, Class. Quantum Grav., 24, S59–S81, (2007). [DOI], [ADS]. (Cited on page 37.)
Pfeiffer, H.P., Teukolsky, S.A. and Cook, G.B., “Quasicircular orbits for spinning binary black holes”, Phys. Rev. D, 62, 104018, (2000). [DOI], [ADS], [gr-qc/0006084]. (Cited on page 11.)
Pfeiffer, H.P. and York Jr, J.W., “Uniqueness and Nonuniqueness in the Einstein Constraints”, Phys. Rev. Lett., 95, 091101, (2005). [DOI]. (Cited on page 19.)
Phinney, E.S., “The rate of neutron star binary mergers in the universe: Minimal predictions for gravity wave detectors”, Astrophys. J. Lett., 380, L17–L21, (1991). [DOI]. (Cited on page 5.)
Piran, T., “The physics of gamma-ray bursts”, Rev. Mod. Phys., 76, 1143, (2005). [DOI]. (Cited on page 9.)
Pretorius, F., “Evolution of Binary Black-Hole Spacetimes”, Phys. Rev. Lett., 95, 121101, (2005). [DOI], [ADS]. (Cited on pages 15, 39, and 40.)
Pretorius, F., “Simulation of binary black hole spacetimes with a harmonic evolution scheme”, Class. Quantum Grav., 23, S529, (2006). [DOI]. (Cited on pages 39 and 40.)
Rantisou, E., Kobayashi, S., Rasio, F.A. and Laguna, P., “Mergers of Black Hole-Neutron Star Binaries. I. Methods and First Results”, Astrophys. J., 680, 1326, (2008). [DOI]. (Cited on page 11.)
Rasio, F.A. and Shapiro, S.L., “Hydrodynamic evolution of coalescing binary neutron stars”, Astrophys. J., 401, 226, (1992). [DOI]. (Cited on page 8.)
Rasio, F.A. and Shapiro, S.L., “Hydrodynamics of binary coalesce: Polytropes with stiff equations of state”, Astrophys. J., 432, 242, (1994). [DOI]. (Cited on page 8.)
Read, J.S., Lackey, B.D., Owen, B.J. and Friedman, J.L., “Constraints on a phenomenologically parametrized neutron-star equation of state”, Phys. Rev. D, 79, 124032, (2009). [DOI]. (Cited on pages 42 and 45.)
Read, J.S., Markakis, C., Shibata, M., Uryū, K., Creighton, J.D.E. and Friedman, J.L., “Measuring the neutron star equation of state with gravitational wave observations”, Phys. Rev. D, 79, 124033, (2009). [DOI]. (Cited on pages 41 and 42.)
Rosswog, S., “Mergers of Neutron Star-Black Hole Binaries with Small Mass Ratios: Nucleosynthesis, Gamma-Ray Bursts, and Electromagnetic Transients”, Astrophys. J., 634, 1202, (2005). [DOI]. (Cited on pages 11 and 14.)
Rosswog, S. and Liebendörfer, M., “High-resolution calculations of merging neutron stars — II. Neutrino emission”, Mon. Not. R. Astron. Soc., 342, 673, (2003). [DOI]. (Cited on page 40.)
Rosswog, S., Speith, R. and Wynn, G.A., “Accretion dynamics in neutron star-black hole binaries”, Mon. Not. R. Astron. Soc., 351, 1121, (2004). [DOI]. (Cited on pages 11 and 14.)
Ruffert, M. and Janka, H.-T., “Colliding neutron stars: Gravitational waves, neutrino emission, and gamma-ray bursts”, Astron. Astrophys., 338, 535–555, (1998). [ADS], [astro-ph/9804132]. (Cited on page 40.)
Ruffert, M. and Janka, H.-T., “Coalescing neutron stars — A step towards physical models. III. Improved numerics and different neutron star masses and spins”, Astron. Astrophys., 380, 544, (2001). [DOI], [astro-ph/0106229]. (Cited on page 40.)
Ruffert, M. and Janka, H.-T., “Polytropic neutron star-black hole merger simulations with a Paczyński-Wiita potential”, Astron. Astrophys., 514, 66, (2010). [DOI]. (Cited on pages 11 and 14.)
Ruffert, M., Janka, H.-T. and Schäfer, G., “Coalescing neutron stars — a step towards physical models. I. Hydrodynamic evolution and gravitational-wave emission”, Astron. Astrophys., 311, 532–566, (1996). [astro-ph/9509006]. (Cited on page 40.)
Ruffert, M., Janka, H.-T., Takahashi, K. and Schäfer, G., “Coalescing neutron stars — a step towards physical models. II. Neutrino emission, neutron tori, and gamma-ray bursts”, Astron. Astrophys., 319, 122, (1997). (Cited on page 40.)
Saijo, M. and Nakamura, T., “Possible Direct Method to Determine the Radius of a Star from the Spectrum of Gravitational Wave Signals”, Phys. Rev. Lett., 85, 2665, (2000). [DOI]. (Cited on page 50.)
Saijo, M. and Nakamura, T., “Possible Direct Method to Determine the Radius of a Star from the Spectrum of Gravitational Wave Signals”, Phys. Rev. D, 63, 064004, (2001). [DOI]. (Cited on page 50.)
Santamaría, L. et al., “Matching post-Newtonian and numerical relativity waveforms: Systematic errors and a new phenomenological model for nonprecessing black hole binaries”, Phys. Rev. D, 82, 064016, (2010). [DOI], [arXiv:1005.3306]. (Cited on page 60.)
Sathyaprakash, B.S. and Schutz, B.F., “Physics, Astrophysics and Cosmology with Gravitational Waves”, Living Rev. Relativity, 12, lrr-2009-2, (2009). [arXiv:0903.0338]. URL (accessed 20 December 2010): http://www.livingreviews.org/lrr-2009-2. (Cited on page 9.)
Scheel, M.A., Boyle, M., Chu, T., Kidder, L.E., Matthews, K.D. and Pfeiffer, H.P., “High-accuracy waveforms for binary black hole inspiral, merger, and ringdown”, Phys. Rev. D, 79, 024003, (2009). [DOI], [arXiv:0810.1767]. (Cited on pages 15 and 40.)
Schnetter, E., Hawley, S.H. and Hawke, I., “Evolutions in 3D numerical relativity using fixed mesh refinement”, Class. Quantum Grav., 21, 1465–1488, (2004). [DOI]. (Cited on page 44.)
Sekiguchi, Y.-I., “An implementation of the microphysics in full general relativity: A general relativistic neutrino leakage scheme”, Class. Quantum Grav., 27, 114107, (2010). [DOI]. (Cited on pages 12, 40, and 43.)
Sekiguchi, Y.-I., “Stellar Core Collapse in Full General Relativity with Microphysics: Formulation and Spherical Collapse Test”, Prog. Theor. Phys., 124, 331, (2010). [DOI]. (Cited on pages 40 and 43.)
Sekiguchi, Y.-I., Kiuchi, K., Kyutoku, K. and Shibata, M., “Gravitational waves and neutrino emission from the merger of binary neutron stars”, Phys. Rev. Lett., 107, 051102, (2011). [DOI], [arXiv:1105.2125]. (Cited on pages 12, 40, and 43.)
Shapiro, S.L. and Teukolsky, S.A., Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects, (Wiley, New York, 1983). [Google Books]. (Cited on pages 5, 8, and 12.)
Shapiro, S.L. and Wasserman, I., “Gravitational radiation from nonspherical infall into black holes”, Astrophys. J., 260, 838–848, (1982). [DOI]. (Cited on page 62.)
Shen, H., Toki, H., Oyamatsu, K. and Sumiyoshi, K., “Relativistic equation of state of nuclear matter for supernova and neutron star”, Nucl. Phys. A, 637, 435–450, (1998). [DOI]. (Cited on pages 43 and 45.)
Shen, H., Toki, H., Oyamatsu, K. and Sumiyoshi, K., “Relativistic Equation of State of Nuclear Matter for Supernova Explosion”, Prog. Theor. Phys., 100, 1013–1031, (1998). [DOI]. (Cited on pages 43 and 45.)
Shibata, M., “Instability of synchronized binary neutron stars in the first post-Newtonian approximation of general relativity”, Prog. Theor. Phys., 96, Binary neutron stars, (1996). [DOI]. (Cited on page 8.)
Shibata, M., “Relativistic Roche-Riemann problem around a black hole”, Prog. Theor. Phys., 96, 917, (1996). [DOI]. (Cited on pages 8 and 10.)
Shibata, M., “Relativistic formalism for computation of irrotational binary stars in quasiequi-librium states”, Phys. Rev. D, 58, 024012, (1998). [DOI]. (Cited on page 22.)
Shibata, M., “Fully General Relativistic Simulation of Coalescing Binary Neutron Stars: Preparatory Tests”, Phys. Rev. D, 60, 104052, (1999). [DOI], [ADS]. (Cited on page 15.)
Shibata, M., Kyutoku, K., Yamamoto, T. and Taniguchi, K., “Gravitational waves from black hole-neutron star binaries: classification of waveforms”, Phys. Rev. D, 79, 044030, (2009). [DOI]. (Cited on pages 15, 38, 55, 58, and 67.)
Shibata, M. and Nakamura, T., “Evolution of three-dimensional gravitational waves: harmonic slicing case”, Phys. Rev. D, 52, 5428–5444, (1995). [DOI], [ADS]. (Cited on page 39.)
Shibata, M. and Taniguchi, K., “Merger of binary neutron stars to a black hole: Disk mass, short gamma-ray bursts, and quasinormal mode ringing”, Phys. Rev. D, 73, 064027, (2006). [DOI]. (Cited on page 15.)
Shibata, M. and Taniguchi, K., “Merger of black hole and neutron star in general relativity: Tidal disruption, torus mass, and gravitational waves”, Phys. Rev. D, 77, 084015, (2008). [DOI], [arXiv:0711.1410]. (Cited on pages 11, 15, 25, and 38.)
Shibata, M., Taniguchi, K. and Uryū, K., “Merger of binary neutron stars of unequal mass in full general relativity”, Phys. Rev. D, 68, 084020, (2003). [DOI], [ADS]. (Cited on page 15.)
Shibata, M., Taniguchi, K. and Uryū, K., “Merger of binary neutron stars with realistic equations of state in full general relativity”, Phys. Rev. D, 71, 084021, (2005). [DOI]. (Cited on pages 15 and 42.)
Shibata, M. and Uryū, K., “Simulation of merging binary neutron stars in full general relativity: Γ = 2 case”, Phys. Rev. D, 61, 064001, (2000). [DOI]. (Cited on page 15.)
Shibata, M. and Uryū, K., “Gravitational waves from the merger of binary neutron stars in a fully general relativistic simulation”, Prog. Theor. Phys., 107, 265–303, (2002). [DOI]. (Cited on page 15.)
Shibata, M. and Uryū, K., “Merger of black hole-neutron star binaries: nonspinning black hole case”, Phys. Rev. D, 74, 121503(R), (2006). [DOI], [ADS]. (Cited on pages 10, 11, 15, 17, 21, 25, 29, 32, 33, 37, and 38.)
Shibata, M. and Uryū, K., “Merger of black hole-neutron star binaries in full general relativity”, Class. Quantum Grav., 24, S125–S137, (2007). [DOI]. (Cited on pages 10, 11, 15, 17, 21, 25, 29, 32, 33, 37, and 38.)
Shibata, M., Uryū, K. and Friedman, J.L., “Deriving formulations for numerical computation of binary neutron stars in quasicircular orbits”, Phys. Rev. D, 70, 044044, (2004). (Cited on pages 22, 27, and 36.)
Stairs, I.H., “Pulsars in Binary Systems: Probing Binary Stellar Evolution and General Relativity”, Science, 304, 547–552, (2004). [DOI]. (Cited on page 5.)
Szilágyi, B., Lindblom, L. and Scheel, M.A., “Simulations of binary black hole mergers using spectral methods”, Phys. Rev. D, 80, 124010, (2009). [DOI]. (Cited on page 40.)
Taniguchi, K., Baumgarte, T.W., Faber, J.A. and Shapiro, S.L., “Black hole-neutron star binaries in general relativity: Effects of neutron star spin”, Phys. Rev. D, 72, 044008, (2005). [DOI], [ADS]. (Cited on page 10.)
Taniguchi, K., Baumgarte, T.W., Faber, J.A. and Shapiro, S.L., “Quasiequilibrium sequences of black-hole-neutron-star binaries in general relativity”, Phys. Rev. D, 74, 041502(R), (2006). [DOI], [ADS]. (Cited on pages 10, 17, 19, 25, 28, and 29.)
Taniguchi, K., Baumgarte, T.W., Faber, J.A. and Shapiro, S.L., “Quasiequilibrium black hole-neutron star binaries in general relativity”, Phys. Rev. D, 75, 084005, (2007). [DOI], [ADS]. (Cited on pages 7, 10, 17, 25, 28, 29, 37, and 59.)
Taniguchi, K., Baumgarte, T.W., Faber, J.A. and Shapiro, S.L., “Relativistic black hole-neutron star binaries in quasiequilibrium: effects of the black hole excision boundary condition”, Phys. Rev. D, 77, 044003, (2008). [DOI], [ADS]. (Cited on pages 7, 10, 17, 25, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, and 59.)
Taniguchi, K. and Gourgoulhon, E., “Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. III. Identical and different mass stars with γ = 2”, Phys. Rev. D, 66, 104019, (2002). [DOI], [ADS]. (Cited on page 28.)
Taniguchi, K. and Gourgoulhon, E., “Various features of quasiequilibrium sequences of binary neutron stars in general relativity”, Phys. Rev. D, 68, 124025, (2003). [DOI], [ADS]. (Cited on page 28.)
Taniguchi, K. and Nakamura, T., “Innermost stable circular orbit od coalescing neutron star-black hole binary — Generalized pseudo-Newtonian potential approach —”, Prog. Theor. Phys., 96, 693, (1996). (Cited on page 10.)
Taniguchi, K. and Shibata, M., “Binary neutron stars in quasi-equilibrium”, Astrophys. J. Suppl. Ser., 188, 187, (2010). [DOI]. (Cited on pages 17, 25, and 33.)
Teukolsky, S.A., “Irrotational binary neutron stars in quasi-equilibrium in general relativity”, Astrophys. J., 504, 442–449, (1998). [DOI]. (Cited on page 22.)
Tsokaros, A.A. and Uryū, K., “Numerical method for binary black hole/neutron star initial data: Code test”, Phys. Rev. D, 75, 044026, (2007). [DOI]. (Cited on page 11.)
Uryū, K. and Eriguchi, Y., “Newtonian models for black hole-gaseous star close binary systems”, Mon. Not. R. Astron. Soc., 303, 329, (1999). [DOI]. (Cited on page 10.)
Uryū, K., Limousin, F., Friedman, J.L., Gourgoulhon, E. and Shibata, M., “Binary Neutron Stars: Equilibrium Models beyond Spatial Conformal Flatness”, Phys. Rev. Lett., 97, 171101, (2006). [DOI], [ADS]. (Cited on page 36.)
Uryū, K., Limousin, F., Friedman, J.L., Gourgoulhon, E. and Shibata, M., “Nonconformally flat initial data for binary compact objects”, Phys. Rev. D, 80, 124004, (2009). [DOI]. (Cited on pages 17, 22, and 36.)
Vallisneri, M., “Prospects for Gravitational-Wave Observations of Neutron-Star Tidal Disruption in Neutron-Star-Black-Hole Binaries”, Phys. Rev. Lett., 84, 3519, (2000). [DOI]. (Cited on pages 9 and 41.)
van Meters, J.R., Baker, J.G., Koppitz, M. and Choi, D-I., “How to move a black hole without excision: Gauge conditions for the numerical evolution of a moving puncture”, Phys. Rev. D, 73, 124011, (2006). [DOI]. (Cited on page 39.)
“Virgo”, project homepage, INFN. URL (accessed 20 December 2010): http://www.virgo.infn.it/. (Cited on page 6.)
Voss, R. and Tauris, T.M., “Galactic distribution of merging neutron stars and black holes — prospects for short gamma-ray burst progenitors and LIGO/VIRGO”, Mon. Not. R. Astron. Soc., 342, 1169–1184, (2003). [DOI], [ADS], [arXiv:astro-ph/0303227]. (Cited on page 5.)
Walsh, D.M., “Non-uniqueness in conformal formulations of the Einstein constraints”, Class. Quantum Grav., 24, 1911, (2007). [DOI]. (Cited on page 19.)
Wiggins, P. and Lai, D., “Tidal interaction between a fluid star and a Kerr black hole in circular orbit”, Astrophys. J., 532, 530, (2000). [DOI]. (Cited on pages 8, 9, 10, and 32.)
Will, C.M., “Gravitational Waves from Inspiralling Compact Binaries: A Post-Newtonian Approach”, in Sasaki, M., ed., Relativistic Cosmology, Proceedings of the 8th Nishinomiya-Yukawa Memorial Symposium, Shukugawa City Hall, Nishinomiya, Hyogo, Japan, 28–29 October, 1993, NYMSS, 8, pp. 83–98, (Universal Academy Press, Tokyo, 1993). [gr-qc/9403033]. (Cited on page 49.)
Will, C.M., Theory and Experiment in Gravitational Physics, (Cambridge University Press, Cambridge; New York, 1993), 2nd edition. [Google Books]. (Cited on page 60.)
Yamamoto, T., Shibata, M. and Taniguchi, K., “Simulating coalescing compact binaries by a new code (SACRA)”, Phys. Rev. D, 78, 064054, (2008). [DOI]. (Cited on pages 38, 44, 55, and 58.)
York Jr, J.W., “Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial-value problem of general relativity”, J. Math. Phys., 14, 456–464, (1973). (Cited on page 18.)
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24–August 4, 1978, pp. 83–126, (Cambridge University Press, Cambridge; New York, 1979). [ADS]. (Cited on pages 27 and 39.)
York Jr, J.W., “Conformal ‘Thin-S and wich’ Data for the Initial-Value Problem of General Relativity”, Phys. Rev. Lett., 82, 1350–1353, (1999). [DOI]. (Cited on pages 17 and 27.)
Zhang, B. and Mészáros, P., “Gamma-ray bursts: Progress, problems, and prospects”, Int. J. Mod. Phys. A, 19, 2385–2472, (2004). [DOI], [astro-ph/0311321]. (Cited on page 9.)
Acknowledgements
We are grateful to M.D. Duez, K. Kyutoku, and Y.T. Liu for reading this article and for providing helpful comments. We also thank M.D. Duez and F. Foucart for providing the data for plotting Figure 20(a). It is also a pleasure to acknowledge K. Kyutoku for his special help in completing many of the figures in this article. This work was supported by Grant-in-Aid for Scientific Research of JSPS (21340051), Grant-in-Aid for Research Activity Start-up of JSPS (22840010), and by Grant-in-Aid for Scientific Research on Innovative Area (20105004) of Japanese MEXT.
Author information
Authors and Affiliations
Corresponding author
Basic Field Equations
Basic Field Equations
In the BSSN-puncture formalism, the typical variables to be evolved are
The typical basic equations are
where \(\tilde \Gamma _{jk}^i\) is the Christoffel symbol associated with \({{\tilde \gamma}_{ij}}\), and
The gauges in the puncture formulation are
where Bi is an auxiliary function and ηB is a constant chosen to be of order 1/m0 with m0 being the total mass of the system.
A point in the BSSN formalism is to rewrite the Ricci tensor, e.g., as
where \({{\tilde R}_{ij}}\) is the Ricci tensor with respect to \({{\tilde \gamma}_{ij}}\) and
Here, \({\tilde D_i}\) is the covariant derivative with respect to \({\tilde \gamma _{ij}}\). Then, \({\tilde R_{ij}}\) is written using \({\tilde \Gamma ^i}\), e.g., as
With this prescription, \({\tilde R_{ij}} \sim - \Delta {\tilde \gamma _{ij}}/2\) in the weak field limit, and thus, Equations (136) and (137 essentially constitute a Klein-Gordon-type wave equations for \({\tilde \gamma _{ij}}\).
In the generalized harmonic GH formalism, the typical variables to be evolved are spacetime metric g μν , and
The evolution equations in the GH formalism are written in first-order form. In contrast to the BSSN formalism, there are several options for the basic equations, in particular, in the choice of the constraint damping terms. The details of the formalism employed in the CCCW and LBPLI groups are described in [129] and [6], respectively. The GH gauge condition is explicitly written as
where \(\Gamma _{kl}^j\) is the Christoffel symbol associated with g μν . A suitable choice for H μ is still under development, e.g., the CCCW group employs a rather phenomenological function [58], and LBPLI employs H μ = 0 [6].
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shibata, M., Taniguchi, K. Coalescence of Black Hole-Neutron Star Binaries. Living Rev. Relativ. 14, 6 (2011). https://doi.org/10.12942/lrr-2011-6
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2011-6
Keywords
Article history
Latest
Coalescence of black hole–neutron star binaries- Published:
- 06 December 2021
- Received:
- 31 March 2021
- Accepted:
- 08 October 2021
DOI: https://doi.org/10.1007/s41114-021-00033-4
Original
Coalescence of Black Hole-Neutron Star Binaries- Published:
- 29 August 2011
- Accepted:
- 07 July 2011
DOI: https://doi.org/10.12942/lrr-2011-6