Abstract
The idea of stable, localized bundles of energy has strong appeal as a model for particles. In the 1950s, John Wheeler envisioned such bundles as smooth configurations of electromagnetic energy that he called geons, but none were found. Instead, particle-like solutions were found in the late 1960s with the addition of a scalar field, and these were given the name boson stars. Since then, boson stars find use in a wide variety of models as sources of dark matter, as black hole mimickers, in simple models of binary systems, and as a tool in finding black holes in higher dimensions with only a single Killing vector. We discuss important varieties of boson stars, their dynamic properties, and some of their uses, concentrating on recent efforts.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Avoid common mistakes on your manuscript.
1 Introduction
Particle-like objects have a very long and broad history in science, arising long before Newton’s corpuscles of light, and spanning the range from fundamental to astronomical. In the mid-1950s, John Wheeler sought to construct stable, particle-like solutions from only the smooth, classical fields of electromagnetism coupled to general relativity [220, 182]. Such solutions would represent something of a “gravitational atom”, but the solutions Wheeler found, which he called geons, were unstable. However, in the following decade, Kaup replaced electromagnetism with a complex scalar field [126], and found Klein-Gordon geons that, in all their guises, have become well-known as today’s boson stars (see Section II of [194] for a discussion of the naming history of boson stars).
As compact, stationary configurations of scalar field bound by gravity, boson stars are called upon to fill a number of different roles. Most obviously, could such solutions actually represent astrophysical objects, either observed directly or indirectly through its gravity? Instead, if constructed larger than a galaxy, could a boson star serve as the dark matter halo that explains the flat rotation curve observed for most galaxies?
The equations describing boson stars are relatively simple, and so even if they do not exist in nature, they still serve as a simple and important model for compact objects, ranging from particles to stars and galaxies. In all these cases, boson stars represent a balance between the dispersive nature of the scalar field and the attraction of gravity holding it together.
This review is organized as follows. The rest of this section describes some general features about boson stars. The system of equations describing the evolution of the scalar field and gravity (i.e., the Einstein-Klein-Gordon equations) are presented in Section 2. These equations are restricted to the spherical symmetric case (with a harmonic ansatz for the complex scalar field and a simple massive potential) to obtain a boson-star family of solutions. To accommodate all their possible uses, a large variety of boson-star types have come into existence, many of which are described in more detail in Section 3. For example, one can vary the form of the scalar field potential to achieve a large range of masses and compactness than with just a mass term in the potential. Certain types of potential admit soliton-like solutions even in the absence of gravity, leading to so-called Q-stars. One can adopt Newtonian gravity instead of general relativity, or construct solutions from a real scalar field instead of a complex one. It is also possible to find solutions coupled to an electromagnetic field or a perfect fluid, leading respectively to charged boson stars and fermion-boson stars. Rotating boson stars are found to have an angular momentum which is not arbitrary, but instead quantized. Multi-state boson stars with more than one complex scalar field are also considered.
We discuss the dynamics of boson stars in Section 4. Arguably, the most important property of boson-star dynamics concerns their stability. A stability analysis of the solutions can be performed either by studying linear perturbations, catastrophe theory, or numerical non-linear evolutions. The latter option allows for the study of the final state of perturbed stars. Possible endstates include dispersion to infinity of the scalar field, migration from unstable to stable configurations, and collapse to a black hole. There is also the question of formation of boson stars. Full numerical evolutions in 3D allow for the merger of binary boson stars, which display a large range of different behaviors as well producing distinct gravitational-wave signatures.
Finally, we review the impact of boson stars in astronomy in Section 5 (as an astrophysical object, black hole mimickers and origin of dark matter) and in mathematics in Section 6 (studies of critical behavior, the Hoop conjecture and higher dimensions). We conclude with some remarks and future directions.
1.1 The nature of a boson star
Boson stars (BS) are constructed with a complex scalar field coupled to gravity (as described in Section 2). A complex scalar field ϕ(t, r) can be decomposed into two real scalar fields ϕR and ϕI mapping every spacetime event to the complex plane
Such a field possesses energy because of its spatial gradients and time derivatives and this energy gravitates holding the star together. Less clear is what supports the star against the force of gravity. Its constituent scalar field obeys a Klein-Gordon wave equation which tends to disperse fields. This is the same dispersion which underlies the Heisenberg uncertainty principle. Indeed, Kaup’s original work [126] found energy eigenstates for a semi-classical, complex scalar field, discovering that gravitational collapse was not inevitable. Ruffini and Bonazzola [188] followed up on this work by quantizing a real scalar field representing some number of bosons and they found the same field equations.
None of this guarantees that such solutions balancing dispersion against gravitational attraction exist. In fact, a widely known theorem, Derrick’s theorem [68] (see also [186]), uses a clever scaling argument to show that no regular, static, nontopological localized scalar field solutions are stable in three (spatial) dimensional flat space. This constraint is avoided by adopting a harmonic ansatz for the complex scalar field
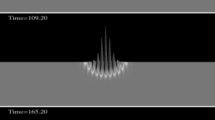
and by working with gravity. Although the field is no longer static, as shown in Section 2 the spacetime remains static. The star itself is a stationary, soliton-like solution as demonstrated in Figure 1.
Demonstration of the solitonic nature of the (mini-)boson star. Shown are snapshots of the magnitude squared of the complex scalar field for a head-on collision of two identical mini-boson stars. The interacting stars display an interference pattern as they pass through each other, recovering their individual identities after the collision. However, note that the BSs have a larger amplitude after their interaction and so are not true solitons. The collision can therefore be considered inelastic. Reprinted with permission from [49]. See also [141] (e.g., Figure 5.12).
There are, of course, many other soliton and soliton-like solutions in three dimensions finding a variety of ways to evade Derrick’s theorem. For example, the field-theory monopole of ’t Hooft and Polyakov is a localized solution of a properly gauged triplet scalar field. Such a solution is a topological soliton because the monopole possesses false vacuum energy which is topologically trapped. The monopole is one among a number of different topological defects that requires an infinite amount of energy to “unwind” the potential energy trapped within (see [218] for a general introduction to defects and the introduction of [189] for a discussion of relevant classical field theory concepts).
In Section 2, we present the underlying equations and mathematical solutions, but here we are concerned with the physical nature of these boson stars. When searching for an actual boson star, we look not for a quantized wave function, or even a semiclassical one. Instead, we search for a fundamental scalar, say the long-sought Higgs boson. The Large Hadron Collider (LHC) hopes to determine the existence and nature of the Higgs, with evidence at the time of writing suggesting a Higgs boson with mass ≈ 125 GeV/c2 [184]. If the Higgs does not ultimately appear, there are other candidates such as an axion particle. Boson stars are then either a collection of stable fundamental bosonic particles bound by gravity, or else a collection of unstable particles that, with the gravitational binding, have an inverse process efficient enough to reach an equilibrium. They can thus be considered a Bose-Einstein condensate (BEC), although boson stars can also exist in an excited state as well.
Indeed, applying the uncertainty principle to a boson star by assuming it to be a macroscopic quantum state results in an excellent estimate for the maximum mass of a BS. One begins with the Heisenberg uncertainty principle of quantum mechanics
and assumes the BS is confined within some radius Δx = R with a maximum momentum of Δp = mc where m is the mass of the constituent particle
This inequality is consistent with the star being described by a Compton wavelength of λC = h/(mc). We look for the maximum possible mass Mmax for the boson star, which will saturate the uncertainty bound and drive the radius of the star towards its Schwarzschild radius RS ≡ 2GM/c2. Substituting yields
which gives an expression for the maximum mass
Recognizing the Planck mass \({M_{{\rm{Planck}}}} \equiv \sqrt {\hbar c/G}\), we obtain the estimate of \({M_{\max}} = 0.5M_{{\rm{Planck}}}^2/m\). This simple estimate indicates that the maximum mass of the BS is inversely related to the mass of the constituent scalar field. We will see below in Section 2 that this inverse relationship continues to hold with the explicit solution of the differential equations for a simple mass term in the potential, but can vary with the addition of self-interaction terms. Indeed depending on the strength of the coupling m and the other parameters of the self-interaction potential, the size and mass of the boson stars can vary from atomic to astrophysical scales. Despite their connection to fundamental physics, one can also view boson stars in analogy with models of neutron stars. In particular, as we discuss in the following sections, both types of stars demonstrate somewhat similar mass versus radius curves for their solutions with a transition in stability at local maxima of the mass. There is also a correspondence between (massless) scalar fields and a stiff, perfect fluid (see Section 2.1 and Appendix A of Ref. [35]), but the correspondence does not mean that the two are equivalent [78]. More than just an analogy, boson stars can serve as a very useful model of a compact star, having certain advantages over a fluid neutron star model: (i) the equations governing its dynamics avoid developing discontinuities, in particular there is no sharp stellar surface, (ii) there is no concern about resolving turbulence, and (iii) one avoids uncertainties in the equation of state.
1.2 Other reviews
A number of other reviews of boson stars have appeared. Most recently, Schunck and Mielke [194] concentrate on the possibility of detecting BS, extending their previous reviews [162, 163]. In 1992, a number of reviews appeared: Jetzer [122] concentrates on the astrophysical relevance of BS (in particular their relevance for explaining dark matter) while Liddle and Madsen [152] focus on their formation. Other reviews include [208, 149].
2 Solving for Boson Stars
In this section, we present the equations governing boson-star solutions, namely the Einstein equations for the geometry description and the Klein-Gordon equation to represent the (complex) scalar field. We refer to this coupled system as the Einstein-Klein-Gordon (EKG) equations.
The covariant equations describing boson stars are presented in Section 2.2, which is followed by choosing particular coordinates consistent with a 3+1 decomposition in Section 2.3. A form for the potential of the scalar field is then chosen and solutions are presented in Section 2.4.
2.1 Conventions
Throughout this review, Roman letters from the beginning of the alphabet a, b, c, … denote space-time indices ranging from 0 to 3, while letters near the middle i, j, k, … range from 1 to 3, denoting spatial indices. Unless otherwise stated, we use units such that ħ = c = 1 so that the Planck mass becomes Mplanck = G−1/2. We also use the signature convention (−, +, +, +) for the metric.
2.2 The Lagrangian, evolution equations and conserved quantities
The EKG evolution equations can be derived from the action [219]
where R is the Ricci scalar of the spacetime represented by the metric gab, and its determinant \(\sqrt {- g}\). The term \({{\mathcal L}_{\mathcal M}}\) describes the matter, which here is that of a complex scalar field, ϕ
where \({\bar \phi}\) is the complex conjugate of the field and V(|ϕ|2) a potential depending only on the magnitude of the scalar field, consistent with the U(1) invariance of the field in the complex plane.
Variation of the action in Eq. (7) with respect to the metric leads to the well-known Einstein equations
where Rab is the Ricci tensor and Tab is the real stress-energy tensor. Eqs. (9) form a system of 10 non-linear partial differential equations for the spacetime metric components gab coupled to the scalar field via the stress-energy tensor given in Eq. (10).
On the other hand, the variation of the action in Eq. (7) with respect to the scalar field ϕ, leads to the Klein-Gordon (KG) equation
An equivalent equation is obtained when varying the action with respect to the complex conjugate \({\bar \phi}\). The simplest potential leading to boson stars is the so-called free field case, where the potential takes the form
with m a parameter that can be identified with the bare mass of the field theory.
According to Noether’s theorem, the invariance of the Klein-Gordon Lagrangian in Eq. (8) under global U(1) transformations ϕ → ϕeiφ implies the existence of a conserved current
satisfying the conservation law
The spatial integral of the time component of this current defines the conserved Noether charge, given by
which can be associated with the total number of bosonic particles [188].
2.3 The 3+1 decomposition of the spacetime
Although the spacetime description of general relativity is very elegant, the covariant form of Einstein equations is not suitable to describe how an initial configuration evolves towards the future. It is, therefore, more intuitive to instead consider a succession of spacetime geometries, where the evolution of a given slice is given by the Einstein equations (for more detailed treatments see [4, 24, 34, 96]). In order to convert the four-dimensional, covariant Einstein equations to a more intuitive “space+time” or 3+1 decomposition, the following steps are taken:
-
specify the choice of coordinates. The spacetime is foliated by a family of spacelike hypersur-faces, which are crossed by a congruence of time lines that will determine our observers (i.e., coordinates). This congruence is described by the vector field ta = αna + βa, where α is the lapse function which measures the proper time of the observers, is the shift vector that measures the displacement of the observers between consecutive hypersurfaces and na is the timelike unit vector normal to the spacelike hypersurfaces.
-
decompose every 4D object into its 3+1 components. The choice of coordinates allows for the definition of a projection tensor \({\gamma ^a}_b \equiv \delta _b^a + {n^a}{n_b}\). Any four-dimensional tensor can be decomposed into 3+1 pieces using the spatial projector to obtain the spatial components, or contracting with na for the time components. For instance, the line element can be written in a general form as
$$d{s^2} = - {\alpha ^2}d{t^2} + {\gamma _{ij}}(d{x^i} + {\beta ^i}dt)(d{x^j} + {\beta ^j}dt).$$(16)The stress-energy tensor can then be decomposed into its various components as
$$\tau \equiv {T^{ab}}{n_a}{n_b},\quad {S_i} \equiv {T_{ab}}{n^a}{\gamma ^a}_i,\quad \,{S_{ij}} \equiv {T_{ab}}{\gamma ^a}_i{\gamma ^b}_j.$$(17) -
write down the field equations in terms of the 3+1 components. Within the framework outlined here, the induced (or equivalently, the spatial 3D) metric and the scalar field ϕ are as yet still unknown (remember that the lapse and the shift just describe our choice of coordinates). In the original 3+1 decomposition (ADM formulation [9]) an additional geometrical tensor \({K_{ij}} \equiv - (1/2){{\mathcal L}_{\rm{n}}}{\gamma _{ij}} = - 1/(2\alpha)({\partial _t} - {{\mathcal L}_\beta}){\gamma _{ij}}\) is introduced to describe the change of the induced metric along the congruence of observers. Loosely speaking, one can view the determination of γij and Kij as akin to the specification of a position and velocity for projectile motion. In terms of the extrinsic curvature and its trace, \({\rm{trK}} \equiv {K_i}^i\), the Einstein equations can be written as
$${R_i}^i+ {({\rm{trK}})^2} - K_i^jK_j^i = 16\pi G\tau$$(18)$${\nabla _j}({K_i}^j - {\rm{trK}}\;\delta _i^j) = 8\pi G{S_i}$$(19)$$({\partial _t} - {{\mathcal L}_\beta}){K_{ij}} = - {\nabla _i}{\nabla _j}\alpha + \alpha \left({{R_{ij}} - 2K_i^k{K_{jk}} + {\rm{trK}}\,{K_{ij}} - 8\pi G\left[ {{S_{ij}} - {{{\gamma _{ij}}} \over 2}({\rm{trS -}}\tau)} \right]} \right)$$(20)In a similar fashion, one can introduce a quantity \(Q \equiv - {{\mathcal L}_{\rm{n}}}\phi\) for the Klein-Gordon equation which reduces it to an equation first order in time, second order in space
$${\partial _t}(\sqrt \gamma Q) - {\partial _i}({\beta ^i}\sqrt \gamma Q) + {\partial _i}\left({\alpha \sqrt \gamma {\gamma ^{ij}}{\partial _j}\phi} \right) = \alpha \sqrt \gamma {{dV} \over {d{{\left\vert \phi \right\vert}^2}}}\phi.$$(21) -
enforce any assumed symmetries. Although the boson star is found by a harmonic ansatz for the time dependence, here we choose to retain the full time-dependence. However, a considerably simplification is provided by assuming that the spacetime is spherically symmetric. Following [141], the most general metric in this case can be written in terms of spherical coordinates as
$$d{s^2} = (- {\alpha ^2} + {a^2}{\beta ^2})d{t^2} + 2{a^2}\beta dt\;dr + {a^2}d{r^2} + {r^2}{b^2}d{\Omega ^2},$$(22)where α(t, r) is the lapse function, β(t, r) is the radial component of the shift vector and a(t, r), b(t, r) represent components of the spatial metric, with dΩ2 the metric of a unit two-sphere. With this metric, the extrinsic curvature only has two independent components \(K_j^i = {\rm{diag(}}{K^r}_r,{K^\theta}_\theta {K^\theta}_\theta)\). The constraint equations, Eqs. (18) and (19), can now be written as
$$- {2 \over {arb}}\left\{{{\partial _r}\left[ {{{{\partial _r}(rb)} \over a}} \right] + {1 \over {rb}}\left[ {{\partial _r}\left({{{rb} \over a}{\partial _r}(rb)} \right) - a} \right]} \right\} + 4{K^r}_r{K^\theta}_\theta + 2{K^\theta}_\theta {K^\theta}_\theta$$(23)$$= {{8\pi G} \over {{a^2}}}\left[ {{{\left\vert \Phi \right\vert}^2} + {{\left\vert \Pi \right\vert}^2} + {a^2}V({{\left\vert \phi \right\vert}^2})} \right]$$(24)$${\partial _r}{K^\theta}_\theta + {{{\partial _r}(rb)} \over {rb}}({K^\theta}_\theta - {K^r}_r) = {{2\pi G} \over a}(\overline \Pi \Phi + \Pi \overline \Phi),$$(25)where we have defined the auxiliary scalar-field variables
$$\Phi \equiv {\partial _r}\phi, \,\quad \Pi \equiv {a \over \alpha}({\partial _t}\phi - \beta {\partial _r}\phi).$$(26)The evolution equations for the metric and extrinsic curvature components reduce to
$${\partial _t}a = {\partial _r}(a\beta) - \alpha a{K^r}_r$$(27)$${\partial _t}b = {\beta \over r}{\partial _r}(rb) - \alpha b{K^\theta}_\theta$$(28)$$\begin{array}{*{20}c} {{\partial _t}{K^r}_r - \beta {\partial _r}{K^r}_r = - {1 \over a}{\partial _r}\left({{{{\partial _r}\alpha} \over a}} \right)} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ {\quad\quad\quad\quad\quad + \alpha \left\{{- {2 \over {arb}}{\partial _r}\left[ {{{{\partial _r}(rb)} \over a}} \right] + {\rm{trK}}{K^r}_r - {{4\pi G} \over {{a^2}}}[2{{\left\vert \Phi \right\vert}^2} + {a^2}V({{\left\vert \phi \right\vert}^2})]} \right\}} \\ {{\partial _t}{K^\theta}_\theta - \beta {\partial _r}{K^\theta}_\theta = {\alpha \over {{{(rb)}^2}}} - {1 \over {a{{(rb)}^2}}}{\partial _r}\left[ {{{\alpha rb} \over a}{\partial _r}(rb)} \right] + \alpha [{\rm{trK}}{K^\theta}_\theta - 4\pi GV({{\left\vert \phi \right\vert}^2})].} \quad\\ \end{array}$$(29)Similarly, the reduction of the Klein-Gordon equation to first order in time and space leads to the following set of evolution equations
$${\partial _t}\phi = \beta \Phi + {\alpha \over a}\Pi$$(30)$${\partial _t}\Phi = {\partial _r}\left({\beta \Phi + {\alpha \over a}\Pi} \right)$$(31)$${\partial _t}\Pi = {1 \over {{{(rb)}^2}}}{\partial _r}\left[ {{{(rb)}^2}\left({\beta \Pi + {\alpha \over a}\Phi} \right)} \right] + 2\left[ {\alpha {K^\theta}_\theta - \beta {{{\partial _r}(rb)} \over {rb}}} \right]\Pi - \alpha a{{dV} \over {d{{\left\vert \phi \right\vert}^2}}}\phi.$$(32)This set of equations, Eqs. (23)–(32), describes general, time-dependent, spherically symmetric solutions of a gravitationally-coupled complex scalar field. In the next section, we proceed to solve for the specific case of a boson star.
2.4 Mini-boson stars
The concept of a star entails a configuration of matter which remains localized. One, therefore, looks for a localized and time-independent matter configuration such that the gravitational field is stationary and regular everywhere. As shown in [89], such a configuration does not exist for a real scalar field. But since the stress-energy tensor depends only on the modulus of the scalar field and its gradients, one can relax the assumption of time-independence of the scalar while retaining a time-independent gravitational field. The key is to assume a harmonic ansatz for the scalar field
where ϕ0 is a real scalar which is the profile of the star and ω is a real constant denoting the angular frequency of the phase of the field in the complex plane.
We consider spherically symmetric, equilibrium configurations corresponding to minimal energy solutions while requiring the spacetime to be static. In Schwarzschild-like coordinates, the general, spherically symmetric, static metric can be written as
in terms of two real metric functions, α and a. The coordinate r is an areal radius such that spheres of constant r have surface area 4πr2. For this reason, these coordinates are often called polar-areal coordinates.
The equilibrium equations are obtained by substituting the metric of Eq. (34) and the harmonic ansatz of Eq. (33) into the spherically symmetric EKG system of Eqs. (27–32) with β = 0, b = 1, resulting in three first order partial differential equations (PDEs)
Notice that these equations hold for any stress-energy contributions and for a generic type of self-potentials V(|ϕ|2). In order to close the system of Eqs. (35–37), we still have to prescribe this potential. The simplest case admitting localized solutions is the free field case of Eq. (12) for which the potential describes a field with mass m and for which the equations can be written as
In order to obtain a physical solution of this system, we have to impose the following boundary conditions,
which guarantee regularity at the origin and asymptotic flatness. For a given central value of the field {ϕc}, we need only to adjust the eigenvalue {ω} to find a solution which matches the asymptotic behavior of Eqs. (44–45). This system can be solved as a shooting problem by integrating from r = 0 towards the outer boundary r = rout. Eq. (39) is linear and homogeneous in α and one is, therefore, able to rescale the field consistent with Eq. (45). We can get rid of the constants in the equations by re-scaling the variables in the following manner
Notice that the form of the metric in Eq. (34) resembles Schwarzschild allowing the association a2 ≡ (1 − 2 M/r)−1, where M is the ADM mass of the spacetime. This allow us to define a more general mass aspect function
which measures the total mass contained in a coordinate sphere of radius r at time t.
In isotropic coordinates, the spherically symmetric metric can be written as
where ψ is the conformal factor. A change of the radial coordinate R = R(r) can transform the solution obtained in Schwarzschild coordinates into isotropic ones, in particular
where the first condition is the initial value to integrate the second equation backwards, obtained by imposing that far away from the boson star the spacetime resembles Schwarzschild solution.
As above, boson stars are spherically symmetric solutions of the Eqs. (38–40) with asymptotic behavior given by Eqs. (41–45). For a given value of the central amplitude of the scalar field ϕ0(r = 0) = ϕc, there exist configurations with some effective radius and a given mass satisfying the previous conditions for a different set of n discrete eigenvalues ω(n). As n increases, one obtains solutions with an increasing number of nodes in ϕ0. The configuration without nodes is the ground state, while all those with any nodes are excited states. As the number of nodes increases, the distribution of the mass as a function of the radius becomes more homogeneous.
As the amplitude ϕc increases, the stable configuration has a larger mass while its effective radius decreases. This trend indicates that the compactness of the boson star increases. However, at some point the mass instead decreases with increasing central amplitude. Similar to models of neutron stars (see Section 4 of [59]), this turnaround implies a maximum allowed mass for a boson star in the ground state, which numerically was found to be \({M_{\max}} = 0.633M_{{\rm{Planck}}}^2/m\). The existence of a maximum mass for boson stars is a relativistic effect, which is not present in the Newtonian limit, while the maximum of baryonic stars is an intrinsic property.
Solutions for a few representative boson stars in the ground state are shown in Figure 2 in isotropic coordinates. The boson stars becomes more compact for higher values of ϕc, implying narrower profiles for the scalar field, larger conformal factors, and smaller lapse functions, as the total mass increases.
Profiles characterizing static, spherically symmetric boson stars with a few different values of the central scalar field (top left). Reprinted with permission from [141].
3 Varieties of Boson Stars
Quite a number of different flavours of boson stars are present in the literature. They can have charge, a fermionic component, or rotation. They can be constructed with various potentials for the scalar field. The form of gravity which holds them together can even be modified to, say, Newtonian gravity or even no gravity at all (Q-balls). To a certain extent, such modifications are akin to varying the equation of state of a normal, fermionic star. Here we briefly review some of these variations, paying particular attention to recent work.
3.1 Self-interaction potentials
Originally, boson stars were constructed with a free-field potential without any kind of self-interaction, obtaining a maximum mass with a dependence \(M \approx M_{{\rm{Planck}}}^2/m\). This mass, for typical masses of bosonic particle candidates, is much smaller than the Chandrasekhar mass \({M_{{\rm{Ch}}}} \approx M_{{\rm{Planck}}}^3/{m^2}\) obtained for fermionic stars, and so they were known as mini-boson stars. In order to extend this limit and reach astrophysical masses comparable to the Chandrasekhar mass, the potential was generalized to include a self-interaction term that provided an extra pressure against gravitational collapse.
Although the first expansion to nonlinear potentials was considered in [161] including fourth and sixth power |ϕ|-terms, a deeper analysis was performed later considering a potential with only the quartic term [57]
with λ a dimensionless coupling constant. Written in terms of a general potential, the EKG equations remain the same. The families of gravitational equilibrium can be parametrized by the single dimensionless quantity Λ ≡ λ/(4π Gm2). The potential of Eq. (51) results in a maximum boson-star mass that now scales as
which is comparable to the Chandrasekhar mass for fermions with mass m/λ1/4 [57]. This self-interaction, therefore, allows much larger masses than the mini-boson stars as long as Λ ≫ 1, an inequality that may be satisfied even when λ ≫ 1 for reasonable scalar boson masses. The maximum mass as a function of the central value of the scalar field is shown in Figure 3 for different values of Λ. The compactness of the most massive stable stars was studied in [8], finding an upper bound M/R ≳ 0.16 for Λ ≫ 1. Figure 4 displays this compactness as a function of Λ along with the compactness of a Schwarzschild BH (black hole) and non-spinning neutron star for comparison.
Left: The mass of the boson star as a function of the central value of the scalar field in adimensional units \({\sigma _c} = \sqrt {4\pi G} {\phi _c}\). Right: Maximum mass as a function of Λ (squares) and the asymptotic Λ → ∞ relation of Eq. (52) (solid curve). Reprinted with permission from [57]; copyright by APS.
The compactness of a stable boson star (black solid line) as a function of the adimensional self-interaction parameter Λ ≡ λ/(4π Gm2). The compactness is shown for the most massive stable star (the most compact BS is unstable). This compactness asymptotes for Λ → ∞ to the value indicated by the red, dashed line. Also shown for comparison is the compactness of a Schwarzschild BH (green dot-dashed line), and the maximum compactness of a non-spinning neutron star (blue dotted line). Reprinted with permission from [8]; copyright by IOP.
Many subsequent papers further analyze the EKG solutions with polynomial, or even more general non-polynomial, potentials. One work in particular [195] studied the properties of the galactic dark matter halos modeled with these boson stars. They found that a necessary condition to obtain stable, compact solutions with an exponential decrease of the scalar field, the series expansion of these potentials must contain the usual mass term m2|ϕ|2.
More exotic ideas similarly try to include a pressure to increase the mass of BSs. Ref. [2] considers a form of repulsive self-interaction mediated by vector mesons within the mean-field approximation. However, the authors leave the solution of the fully nonlinear system of the KleinGordon and Proca equations to future work. Ref. [18] models stars made from the condensation of axions, using the semi-relativistic approach with two different potentials. Mathematically this approach involves averages such that the equations are equivalent to assuming the axion is constituted by a complex scalar field with harmonic time dependence.
Other generalizations of the potential allow for the presence of nontopological soliton solutions even in the absence of gravity, with characteristics quite different than those of the mini-boson stars. In order to obtain these solutions the potential must satisfy two conditions. First, it must be a function of |ϕ|2 to preserve the global U(1) invariance. Second, the potential should have an attractive term, bounded from below and positive for |ϕ| → ∞. These conditions imply a potential of at least sixth order, a condition that is satisfied by the typical degenerate vacuum form [147, 89, 90]
for which the potential has two degenerate minima at ±ϕ0. The case |ϕ| = 0 corresponds to the true vacuum state, while |ϕ| = ϕ0 represents the degenerate vacuum state.
The resulting soliton solution can be split in three different regions. When gravity is negligible, the interior solution satisfies ϕ ≈ ϕ0, followed by a shell of width 1/m over which ϕ changes from ϕ0 to zero, and an exterior that is essentially vacuum. This potential leads to a different scaling of the mass and the radius than that of the ground state [149]
There is another type of non-topological soliton star, called Q-stars [155], which also admits soliton solutions in the absence of gravity (i.e., Q-balls [56, 149]). The potential, besides being also a function of |ϕ|2, must satisfy the following conditions: it must behave like ≈ ϕ2 near ϕ = 0, it has to be bounded < ϕ2 in an intermediate region and must be larger > ϕ2 for |ϕ| → ∞. The Q-stars also have three regions; an interior solution of radius \(R \approx {M_{{\rm{Planck}}}}/\phi _0^2\), (i.e., ϕ0 ≈ m is the free particle inverse Compton wavelength) a very thin surface region of thickness 1/ϕ0, and finally the exterior solution without matter, which reduces to Schwarzschild in spherical symmetry. The mass of these Q-stars scales now as \(M_{{\rm{Planck}}}^3/\phi _0^2\). The stability of these Q-stars has been studied recently using catastrophe theory, such as [209, 135]. Rotating, axisymmetric Q-balls were constructed in [133, 134]. Related, rotating solutions in 2+1 with the signum-Gordon equation instead of the KG equation are found in [10].
Other interesting works have studied the formation of Q-balls by the Affleck-Dine mechanism [125], their dynamics in one, two and three spatial dimensions [22], and their viability as a self-interacting dark matter candidate [139].
Ref. [29] considers a chemical potential to construct BSs, arguing that the effect of the chemical potential is to reduce the parameter space of stable solutions. Related work modifies the kinetic term of the action instead of the potential. Ref. [1] studies the resulting BSs for a class of K field theories, finding solutions of two types: (i) compact balls possessing a naked singularity at their center and (ii) compact shells with a singular inner boundary which resemble black holes. Ref. [3] considers coherent states of a scalar field instead of a BS within k-essence in the context of explaining dark matter. Ref. [72] modifies the kinetic term with just a minus sign to convert the scalar field to a phantom field. Although, a regular real scalar field has no spherically symmetric, local static solutions, they find such solutions with a real phantom scalar field.
3.2 Newtonian boson stars
The Newtonian limit of the Einstein-Klein-Gordon Eqs. (9–11) can be derived by assuming that the spacetime metric in the weak field approximation can be written as
where V is the Newtonian gravitational potential. In this limit, the Einstein equations reduce to the Poisson equation
Conversely, by assuming that
in addition to the weak limit of Eq. (55), the Klein-Gordon equation reduces to
which is just the Schrödinger equation with ħ = 1. Therefore, the EKG system is reduced in the Newtonian limit to the Schrödinger-Poisson (SP) system [98].
The initial data is obtained by solving an eigenvalue problem very similar to the one for boson stars, with similar assumptions and boundary conditions. The solutions also share similar features and display a similar behavior. A nice property of the Newtonian limit is that all the solutions can be obtained by rescaling from one known solution [98],
where \(N \equiv m\int {d{x^3}\phi \bar \phi}\) is the Newtonian number of particles.
The possibility of including self-interaction terms in the potential was considered in [106], studying also the gravitational cooling (i.e., the relaxation and virialization through the emission of scalar field bursts) of spherical perturbations. Non-spherical perturbations were further studied in [27], showing that the final state is a spherically symmetric configuration. Single Newtonian boson stars were studied in [98], either when they are boosted with/without an external central potential. Rotating stars were first successfully constructed in [203] within the Newtonian approach. Numerical evolutions of binary boson stars in Newtonian gravity are discussed in Section 4.2.
Recent work by Chavanis with Newtonian gravity solves the Gross-Pitaevskii equation, a variant of Eq. (58) which involves a pseudo-potential for a Bose-Einstein condensate, to model either dark matter or compact alternatives to neutron stars [46, 45, 47].
Much recent work considers boson stars from a quantum perspective as a Bose-Einstein condensate involving some number, N, of scalar fields. Ref. [160] studies the collapse of boson stars mathematically in the mean field limit in which N → ∞. Ref. [130] argues for the existence of bosonic atoms instead of stars. Ref. [16] uses numerical methods to study the mean field dynamics of BSs.
3.3 Charged boson stars
Charged boson stars result from the coupling of the boson field to the electromagnetic field [123]. The coupling between gravity and a complex scalar field with a U(1) charge arises by considering the action of Eq. 7 with the following matter Lagrangian density
where e is the gauge coupling constant. The Maxwell tensor Fab can be decomposed in terms of the vector potential Aa
The system of equations obtained by performing the variations on the action forms the Einstein-Maxwell-Klein-Gordon system, which contains the evolution equations for the complex scalar field ϕ, the vector potential Aa and the spacetime metric gab [179].
Because a charged BS may be relevant for a variety of scenarios, we detail the resulting equations. For example, cosmic strings are also constructed from a charged, complex scalar field and obeys these same equations. It is only when we choose the harmonic time dependence of the scalar field that we distinguish from the harmonic azimuth of the cosmic string [218]. The evolution equations for the scalar field and for the Maxwell tensor are
Notice that the vector potential is not unique; we can still add any curl-free components without changing the Maxwell equations. The gauge freedom can be fixed by choosing, for instance, the Lorentz gauge ∇aAa = 0. Within this choice, which sets the first time derivative of the time component A0, the Maxwell equations reduce to a set of wave equations in a curved background with a non-linear current. This gauge choice resembles the harmonic gauge condition, which casts the Einstein equations as a system of non-linear, wave equations [219].
Either from Noether’s theorem or by taking an additional covariant derivative of Eq. (63), one obtains that the electric current Ja follows a conservation law. The spatial integral of the time component of this current, which can be identified with the total charge Q, is conserved. This charge is proportional to the number of particles, Q = e N. The mass M and the total charge Q can be calculated by associating the asymptotic behavior of the metric with that of Reissner-Nordström metric,
which is the unique solution at large distances for a scalar field with compact support.
We look for a time independent metric by first assuming a harmonically varying scalar field as in Eq. (33). We work in spherical coordinates and assume spherical symmetry. With a proper gauge choice, the vector potential takes a particularly simple form with only a single, non-trivial component Aa = (A0(r), 0, 0, 0). This choice implies an everywhere vanishing magnetic field so that the electromagnetic field is purely electric. The boundary conditions for the vector potential are obtained by requiring the electric field to vanish at the origin because of regularity, ∂r A0(r = 0) = 0. Because the electromagnetic field depends only on derivatives of the potential, we can use this freedom to set A0(∞) = 0 [123].
With these conditions, it is possible to find numerical solutions in equilibrium as described in Ref. [123]. Solutions are found for \({{\tilde e}^2} \equiv {e^2}M_{{\rm{Planck}}}^2/(8\pi {m^2}) < 1/2\). For \({{\tilde e}^2} > 1/2\) the repulsive Coulomb force is bigger than the gravitational attraction and no solutions are found. This bound on the BS charge in terms of its mass ensures that one cannot construct an overcharged BS, in analogy to the overcharged monopoles of Ref. [154]. An overcharged monopole is one with more charge than mass and is, therefore, susceptible to gravitational collapse by accreting sufficient (neutral) mass. However, because its charge is higher than its mass, such collapse might lead to an extremal Reissner-Nordström BH, but BSs do not appear to allow for this possibility. Interestingly, Ref. [190] finds that if one removes gravity, the obtained Q-balls may have no limit on their charge.
The mass and the number of particles are plotted as a function of ϕc for different values of \({\tilde e}\) in Figure 5. Trivially, for \(\tilde e = 0\) the mini-boson stars of Section (2.4) are recovered. Excited solutions with nodes are qualitatively similar [123]. The stability of these objects has been studied in [119], showing that the equilibrium configurations with a mass larger than the critical mass are dynamically unstable, similar to uncharged BSs.
The mass (solid) and the number of particles (dashed) versus central scalar value for charged boson stars with four values of \({\tilde e}\) as defined in Section 3.3. The mostly-vertical lines crossing the four plots indicate the solution for each case with the maximum mass (solid) and maximum particle number (dashed). Reprinted with permission from [123]; copyright by Elsevier.
Recent work with charged BSs includes the publication of Maple [157] routines to study boson nebulae charge [63, 169, 168]
Other work generalizes the Q-balls and Q-shells found with a certain potential, which leads to the signum-Gordon equation for the scalar field [131, 132]. In particular, shell solutions can be found with a black hole in its interior, which has implications for black hole scalar hair (for a review of black hole uniqueness see [113]).
One can also consider Q-balls coupled to an electromagnetic field, a regime appropriate for particle physics. Within such a context, Ref. [76] studies the chiral magnetic effect arising from a Q-ball. Other work in Ref. [36] studies charged, spinning Q-balls.
3.4 Oscillatons
As mentioned earlier, it is not possible to find time-independent, spacetime solutions for a real scalar field. However, there are non-singular, time-dependent near-equilibrium configurations of self-gravitating real scalar fields, which are known as oscillatons [197]. These solutions are similar to boson stars, with the exception that the spacetime must also have a time dependence in order to avoid singularities.
In this case, the system is still described by the EKG Eqs. (27–32), with the the additional simplification that the scalar field is strictly real, \(\phi = \bar \phi\). In order to find equilibrium configurations, one expands both metric components {A(r, t) ≡ a2, C(r, t) ≡ (a/α)2} and the scalar field ϕ(r, t) as a truncated Fourier series
where ω is the fundamental frequency and jmax is the mode at which the Fourier series are truncated. As noted in Ref. [216, 5], the scalar field consists only of odd components while the metric terms consist only of even ones. Solutions are obtained by substituting the expansions of Eq. (65) into the spherically symmetric Eqs. (27–32). By matching terms of the same frequency, the system of equations reduce to a set of coupled ODEs. The boundary conditions are determined by requiring regularity at the origin and that the fields become asymptotically flat at large radius. These form an eigenvalue problem for the coefficients {ϕ2j−1(r = 0), (r = 0), C2j(r = 0)} corresponding to a given central value ϕ1(r = 0). As pointed out in [216], the frequency ω is determined by the coefficient C0(∞) and is, therefore, called an output value. Although the equations are non-linear, the Fourier series converges rapidly, and so a small value of jmax usually suffices.
A careful analysis of the high frequency components of this construction reveals difficulties in avoiding infinite total energy while maintaining the asymptotically flat boundary condition [172]. Therefore, the truncated solutions constructed above are not exactly time periodic. Indeed, very accurate numerical work has shown that the oscillatons radiate scalar field on extremely long time scales while their frequency increases [84, 97]. This work finds a mass loss rate of just one part in 1012 per oscillation period, much too small for most numerical simulations to observe. The solutions are, therefore, only near-equilibrium solutions and can be extremely long-lived.
Although the geometry is oscillatory in nature, these oscillatons behave similar to BSs. In particular, they similarly transition from long-lived solutions to a dynamically unstable branch separated at the maximum mass \({M_{\max}} = 0.607M_{{\rm{Planck}}}^2/m\). Figure 6 displays the total mass curve, which shows the mass as a function of central value. Compact solutions can be found in the Newtonian framework when the weak field limit is performed appropriately, reducing to the so-called Newtonian oscillations [216]. The dynamics produced by perturbations are also qualitatively similar, including gravitational cooling, migration to more dilute stars, and collapse to black holes [5]. More recently, these studies have been extended by considering the evolution in 3D of excited states [13] and by including a quartic self-interaction potential [217]. In [129], a variational approach is used to construct oscillatons in a reduced system similar to that of the sine-Gordon breather solution.
Top: Total mass (in units of \(M_{{\rm{Planck}}}^2/m\)) and fundamental frequency of an oscillaton as a function of the central value of the scalar field ϕ1(r = 0). The maximum mass is \({M_{\max}} = 0.607M_{{\rm{Planck}}}^2/m\). Bottom: Plot of the total mass versus the radius at which grr achieves its maximum. Reprinted with permission from [5]; copyright by IOP.
Closely related, are oscillons that exist in flatspace and that were first mentioned as “pulsons” in 1977 [33]. There is an extensive literature on such solutions, many of which appear in [79]. A series of papers establishes that oscillons similarly radiate on very long time scales [79, 80, 81, 82]. An interesting numerical approach to evolving oscillons adopts coordinates that blueshift and damp outgoing radiation of the massive scalar field [115, 117]. A detailed look at the long term dynamics of these solutions suggests the existence of a fractal boundary in parameter space between oscillatons that lead to expansion of a true-vacuum bubble and those that disperse [116].
3.5 Rotating boson stars
Boson stars with rotation were not explored until the mid-1990s because of the lack of a strong astrophysical motivation and the technical problems with the regularization along the axis of symmetry. The first equilibrium solutions of rotating boson stars were obtained within the Newtonian gravity [203]. In order to generate axisymmetric time-independent solutions with angular momentum, one is naturally lead to the ansatz
where ϕ0(r, θ) is a real scalar representing the profile of the star, ω is a real constant denoting the angular frequency of the field and k must be an integer so that the field ϕ is not multivalued in the azimuthal coordinate φ. This integer is commonly known as the rotational quantum number.
General relativistic rotating boson stars were later found [193, 222] with the same ansatz of Eq. (67). To obtain stationary axially symmetric solutions, two symmetries were imposed on the spacetime described by two commuting Killing vector fields ξ = ∂t and η = ∂φ in a system of adapted (cylindrical) coordinates {t, r, θ, φ}. In these coordinates, the metric is independent of t and φ and can be expressed in isotropic coordinates in the Lewis-Papapetrou form
where f, l, g and Ω are metric functions depending only on r and θ. This means that we have to solve five coupled PDEs, four for the metric and one for the Klein-Gordon equation; these equations determine an elliptic quadratic eigenvalue problem in two spatial dimensions. Near the axis, the scalar field behaves as
so that for k > 0 the field vanishes near the axis. Note that is some arbitrary function different for different values of k but no sum over k is implied in Eq. (69). This implies that the rotating star solutions have toroidal level surfaces instead of spheroidal ones as in the spherically symmetric case k = 0. In this case the metric coefficients are simplified, namely g = 1, Ω = 0 and f = f(r), l = l(r).
The entire family of solutions for k = 1 and part of k = 2 was computed using the self-consistent field method [222], obtaining a maximum mass \({M_{\max}} = 1.31M_{{\rm{Planck}}}^2/m\). Both families were completely computed in [141] using faster multigrid methods, although there were significant discrepancies in the maximum mass, which indicates a problem with the regularity condition on the z-axis. The mass M and angular momentum J for stationary asymptotically flat spacetimes can be obtained from their respective Komar expressions. They can be read off from the asymptotic expansion of the metric functions f and Ω
Alternatively, using the Tolman expressions for the angular momentum and the Noether charge relation in Eq. 15, one obtains an important quantization relation for the angular momentum [222]
for integer values of k. This remarkable quantization condition for this classical solution also plays a role in the work of [69] discussed in Section 6.3. Figure 7 shows the scalar field for two different rotating BSs.
The scalar field in cylindrical coordinates ϕ(ρ, z) for two rotating boson-star solutions: (left) k = 1 and (right) k = 2. The two solutions have roughly comparable amplitudes in scalar field. Note the toroidal shape. Reprinted with permission from [141].
Recently, their stability properties were found to be similar to nonrotating stars [135]. Rotating boson stars have been shown to develop a strong ergoregion instability when rapidly spinning on short characteristic timescales (i.e., 0.1 seconds −1 week for objects with mass M = 1−106 M⊙ and angular momentum J > 0.4 GM2), indicating that very compact objects with large rotation are probably black holes [44].
More discussion concerning the numerical methods and limitations of some of these approaches can be found in Lai’s PhD thesis [141].
3.6 Fermionic-bosonic stars
The possibility of compact stellar objects made with a mixture of bosonic and fermionic matter was studied in Refs. [111, 112]. In the simplest case, the boson component interacts with the fermionic component only via the gravitational field, although different couplings were suggested in [112] and have been further explored in [66, 180]. Such a simple interaction is, at the very least, consistent with models of a bosonic dark matter coupling only gravitationally with visible matter, and the idea that such a bosonic component would become gravitationally bound within fermionic stars is arguably a natural expectation.
One can consider a perfect fluid as the fermionic component such that the stress-energy tensor takes the standard form
where μ is the energy density, p is the pressure of the fluid and ua its four-velocity. Such a fluid requires an equation of state to close the system of equations (see Ref. [85] for more about fluids in relativity). In most work with fermionic-boson stars, the fluid is described by a degenerate, relativistic Fermi gas, so that the pressure is given by the parametric equation of state of Chan-drasekhar
where \(K = m_n^4/(32{\pi ^2})\) and mn the mass of the fermion. The parameter t is given by
where po is the maximum value of the momentum in the Fermi distribution at radius r.
The perfect fluid obeys relativistic versions of the Euler equations, which account for the conservation of the fluid energy and momentum, plus the conservation of the baryonic number (i.e., mass conservation). The complex scalar field representing the bosonic component is once again described by the Klein-Gordon equation. The spacetime is computed through the Einstein equations with a stress-energy tensor, which is a combination of the complex scalar field and the perfect fluid
After imposing the harmonic time dependence of Eq. (33) on the complex scalar field, assuming a static metric as in Eq. (34) and the static fluid ua = 0, one obtains the equations describing equilibrium fermion-boson configurations
These equations can be written in adimensional form by rescaling the variables by introducing the following quantities
By varying the central value of the fermion density μ(r = 0) and the scalar field ϕ(r = 0), one finds stars dominated by either bosons or fermions, with a continuous spectrum in between.
It was shown that the stability arguments made with boson stars can also be applied to these mixed objects [121]. The existence of slowly rotating fermion-boson stars was shown in [65], although no solutions were found in previous attempts [136]. Also see [73] for unstable solutions consisting of a real scalar field coupled to a perfect fluid with a polytropic equation of state.
3.7 Multi-state boson stars
It turns out that excited BSs, as dark matter halo candidates, provide for flatter, and hence more realistic, galactic rotation curves than ground state BSs. The problem is that they are generally unstable to decay to their ground state. Combining excited states with the ground states in what are called multi-state BSs is one way around this.
Although bosons in the same state are indistinguishable, it is possible to construct non-trivial configurations with bosons in different excited states. A system of bosons in P different states that only interact with each other gravitationally can be described by the following Lagrangian density
where ϕ(n) is the particular complex scalar field representing the bosons in the n-state with n − 1 nodes. The equations of motion are very similar to the standard ones described in Section 2.2, with two peculiarities: (i) there are n independent KG equations (i.e., one for each state) and (ii) the stress-energy tensor is now the sum of contributions from each mode. Equilibrium configurations for this system were found in [25].
In the simplest case of a multi-state boson, one has the ground state and the first excited state. Such configurations are stable if the number of particles in the ground state is larger than the number of particles in the excited state [25, 7]
This result can be understood as the ground state deepens the gravitational potential of the excited state, and thereby stabilizing it. Unstable configurations migrate to a stable one via a flip-flop of the modes; the excited state decays, while the ground jumps to the first exited state, so that the condition (78) is satisfied. An example of this behavior can be observed in Figure 8.
Left: The maximum of the central value of each of the two scalar fields constituting the multi-state BS for the fraction η = 3, where η ≡ N(2)/N(1) defines the relative “amount” of each state. Right: The frequencies associated with each of the two states of the multi-state BS. At t = 2000, there is a flip in which the excited state (black solid) decays and the scalar field in the ground state (red dashed) becomes excited. Discussed in Section 3.7. Reprinted with permission from [25]; copyright by APS.
Similar results were found in the Newtonian limit [215], however, with a slightly higher stability limit N(1) ≥ 1.13 N(2). This work stresses that combining several excited states makes it possible to obtain flatter rotation curves than only with ground state, producing better models for galactic dark matter halos (see also discussion of boson stars as an explanation of dark matter in Section 5.3).
Ref. [110] considers two scalar fields describing boson stars that are phase shifted in time with respect to each other, studying the dynamics numerically. In particular, one can consider multiple scalar fields with an explicit interaction (beyond just gravity) between them, say V (|ϕ(1)| (|ϕ(2)|. Refs. [37, 38] construct such solutions, considering the individual particle-like configurations for each complex field as interacting with each other.
3.8 Alternative theories of gravity
Instead of modifying the scalar field potential, one can instead consider alternative theories of gravity. Constraints on such theories are already significant given the great success of general relativity [221]. However, the fast advance of electromagnetic observations and the anticipated gravitational-wave observations promise much more in this area, in particular in the context of compact objects that probe strong-field gravity.
An ambitious effort is begun in Ref. [176], which studies a very general gravitational Lagrangian (“extended scalar-tensor theories”) with both fluid stars and boson stars. The goal is for observations of compact stars to constrain such theories of gravity.
It has been found that scalar tensor theories allow for spontaneous scalarization in which the scalar component of the gravity theory transitions to a non-trivial configuration analogously to ferromagnetism with neutron stars [62]. Such scalarization is also found to occur in the context of boson-star evolution [6].
Boson stars also occur within conformal gravity and with scalar-tensor extensions to it [40, 41].
One motivation for alternative theories is to explain the apparent existence of dark matter without resorting to some unknown dark matter component. Perhaps the most well known of these is MOND (modified Newtonian dynamics) in which gravity is modified only at large distances [164, 165] (for a review see [77]). Boson stars are studied within TeVeS (Tensor-Vector-Scalar), a relativistic generalization of MOND [58]. In particular, their evolutions of boson stars develop caustic singularities, and the authors propose modifications of the theory to avoid such problems.
3.9 Gauged boson stars
In 1988, Bartnik and McKinnon published quite unexpected results showing the existence of particle-like solutions within SU(2) Yang-Mills coupled to gravity [20]. These solutions, although unstable, were unexpected because no particle-like solutions are found in either the Yang-Mills or gravity sectors in isolation. Recall also that no particle-like solutions were found with gravity coupled to electromagnetism in early efforts to find Wheeler’s geon (however, see Section 6.3 for discussion of Ref. [70], which finds geons within AdS).
Bartnik and McKinnon generalize from the Abelian U(1) gauge group to the non-Abelian SU(2) group and thereby find these unexpected particle-like solutions. One can consider, as does Ref. [194] (see Section IIp), these globally regular solutions (and their generalizations to SU(n) for n > 2) as gauged boson stars even though these contain no scalar field. One can instead explicitly include a scalar field doublet coupled to the Yang-Mills gauge field [39] as perhaps a more direct generalization of the (U(1)) charged boson stars discussed in Section 3.3.
Ref. [74] studies BSs formed from a gauge condensate of an SU(3) gauge field, and Ref. [41] extends the Bartnik-McKinnon solutions to conformal gravity with a Higgs field [41].
4 Dynamics of Boson Stars
In this section, the formation, stability and dynamical evolution of boson stars are discussed. One approach to the question of stability considers small perturbations around an equilibrium configuration, so that the system remains in the linearized regime. Growing modes indicate instability. However, a solution can be linearly stable and yet have a nonlinear instability. One example is Minkowski space, which, under small perturbations, relaxes back to flat, but, for sufficiently large perturbations, leads to black-hole formation, decidedly not Minkowski. To study nonlinear stability, other methods are needed. In particular, full numerical evolutions of the Einstein-KleinGordon (EKG) equations are quite useful for understanding the dynamics of boson stars.
4.1 Gravitational stability
A linear stability analysis consists of studying the time evolution of infinitesimal perturbations about an equilibrium configuration, usually with the additional constraint that the total number of particles must be conserved. In the case of spherically symmetric, fermionic stars described by perfect fluid, it is possible to find an eigenvalue equation for the perturbations that determines the normal modes and frequencies of the radial oscillations (see, for example, Ref. [86]). Stability theorems also allow for a direct characterization of the stability branches of the equilibrium solutions [91, 60]. Analogously, one can write a similar eigenvalue equation for boson stars and show the validity of similar stability theorems. In addition to these methods, the stability of boson stars has also been studied using two other, independent methods: by applying catastrophe theory and by solving numerically the time dependent Einstein-Klein-Gordon equations. All these methods agree with the results obtained in the linear stability analysis.
4.1.1 Linear stability analysis
Assume that a spherically symmetric boson star in an equilibrium configuration is perturbed only in the radial direction. The equations governing these small radial perturbations are obtained by linearizing the system of equations in the standard way; expand the metric and the scalar field functions to first order in the perturbation and neglect higher order terms in the equations [93, 118]. Considering the collection of fields for the system fi, one expands them in terms of the background solution 0fi and perturbation as
which assumes harmonic time dependence for the perturbation. Substitution of this expansion into the system of equations then provides a linearized system, which reduces to a set of coupled equations that determines the spectrum of modes 1fi and eigenvalues σ2
where Lij is a differential operator containing partial derivatives and Mij is a matrix depending on the background equilibrium fields 0fi. Solving this system, known as the pulsation equation, produces the spectrum of eigenmodes and their eigenvalues σ.
The stability of the star depends crucially on the sign of the smallest eigenvalue. Because of time reversal symmetry, only σ2 enters the equations [148], and we label the smallest eigenvalue \(\sigma _0^2\). If it is negative, the eigenmode grows exponentially with time and the star is unstable. On the other hand, for positive eigenvalues the configuration has no unstable modes and is therefore stable. The critical point at which the stability transitions from stable to unstable, therefore, occurs when the smallest eigenvalue vanishes, σ0 = 0.
Equilibrium solutions can be parametrized with a single variable, such as the central value of the scalar field ϕc, and so we can write M = M(ϕc) and N = N (ϕc). Stability theorems then indicate that transitions between stable and unstable configurations occur only at critical points of the parameterization (M′(ϕc) = N′(ϕc) = 0) [60, 91, 107, 207]. Linear perturbation analysis provides a more detailed picture such as the growth rates and the eigenmodes of the perturbations.
Ref. [94] carries out such an analysis for perturbations that conserve mass and charge. They find the first three perturbative modes and their growth rates, and they identify at which precise values of ϕc these modes become unstable. Starting from small values, they find that ground state BSs are stable up to the critical point of maximum mass. Further increases in the central value subsequently encounter additional unstable modes. This same type of analysis applied to excited state BSs showed that the same stability criterion applies for perturbations that conserve the total particle number [120]. For more general perturbations that do not conserve particle number, excited states are generally unstable to decaying to the ground state.
A more involved analysis by [148] uses a Hamiltonian formalism to study BS stability. Considering first order perturbations that conserve mass and charge (δN = 0), their results agree with those of [94, 120]. However, they extend their approach to consider more general perturbations, which do not conserve the total number of particles (i.e., δN ≠ 0). To do so, they must work with the second order quantities. They found complex eigenvalues for the excited states that indicate that excited state boson stars are unstable. More detail and discussion on the different stability analysis can be found in Ref. [122].
Catastrophe theory is part of the study of dynamical systems that began in the 1960s and studies large changes in systems resulting from small changes to certain important parameters (for a physics-oriented review see [204]). Its use in the context of boson stars is to evaluate stability, and to do so one constructs a series of solutions in terms of a limited and appropriate set of parameters. Under certain conditions, such a series generates a curve smooth everywhere except for certain points. Within a given smooth expanse between such singular points, the solutions share the same stability properties. In other words, bifurcations occur at the singular points so that solutions after the singularity gain an additional, unstable mode. Much of the recent work in this area confirms the previous conclusions from linear perturbation analysis [209, 210, 211, 212] and from earlier work with catastrophe theory [140].
Another recent work using catastrophe theory finds that rotating stars share a similar stability picture as nonrotating solutions [135]. However, only fast spinning stars are subject to an ergoregion instability [44].
4.1.2 Non-linear stability of single boson stars
The dynamical evolution of spherically symmetric perturbations of boson stars has also been studied by solving numerically the Einstein-Klein-Gordon equations (Section 2.3), or its Newtonian limit (Section 3.2), the Schrödinger-Poisson system. The first such work was Ref. [196] in which the stability of the ground state was studied by considering finite perturbations, which may change the total mass and the particle number (i.e., δN ≠ 0 and δM ≠ 0). The results corroborated the linear stability analysis in the sense that they found a stable and an unstable branch with a transition between them at a critical value, ϕcrit, of the central scalar field corresponding to the maximal BS mass \({M_{\max}} = 0.633M_{{\rm{Planck}}}^2/m\).
The perturbed configurations of the stable branch may oscillate and emit scalar radiation maintaining a characteristic frequency ν, eventually settling into some other stable state with less mass than the original. This characteristic frequency can be approximated in the non-relativistic limit as [196]
where R is the effective radius of the star and M its total mass. Scalar radiation is the only damping mechanism available because spherical symmetry does not allow for gravitational radiation and because the Klein-Gordon equation has no viscous or dissipative terms. This process was named gravitational cooling, and it is extremely important in the context of formation of compact bosonic objects [198] (see below). The behavior of perturbed solutions can be represented on a plot of frequency versus effective mass as in Figure 9. Perturbed stars will oscillate with a frequency below its corresponding solid line and they radiate scalar field to infinity. As they do so, they lose mass by oscillating at constant frequency, moving leftward on the plot until they settle on the stable branch of (unperturbed) solutions.
Oscillation frequencies of various boson stars are plotted against their mass. Also shown are the oscillation frequencies of unstable BSs obtained from the fully nonlinear evolution of the dynamical system. Unstable BSs are observed maintaining a constant frequency as they approach a stable star configuration. Reprinted with permission from [196]; copyright by APS.
The perturbed unstable configurations will either collapse to a black hole or migrate to a stable configuration, depending on the nature of the initial perturbation. If the density of the star is increased, it will collapse to a black hole. On the other hand, if it is decreased, the star explodes, expanding quickly as it approaches the stable branch. Along with the expansion, energy in the form of scalar field is radiated away, leaving a very perturbed stable star, less massive than the original unstable one.
This analysis was extended to boson stars with self-interaction and to excited BSs in Ref. [15], showing that both branches of the excited states were intrinsically unstable under generic perturbations that do not preserve M and N. The low density excited stars, with masses close to the ground state configurations, will evolve to ground state boson stars when perturbed. The more massive configurations form a black hole if the binding energy EB = M − Nm is negative, through a cascade of intermediate states. The kinetic energy of the stars increases as the configuration gets closer to Eb = 0, so that for positive binding energies there is an excess of kinetic energy that tends to disperse the bosons to infinity. These results are summarized in Figure 10, which shows the time scale of the excited star to decay to one of these states.
The instability time scale of an excited boson star (the first excitation) to one of three end states: (i) decay to the ground state, (ii) collapse to a black hole, or (iii) dispersal. Reprinted with permission from [15]; copyright by APS.
More recently, the stability of the ground state was revisited with 3D simulations using a Cartesian grid [102]. The Einstein equations were written in terms of the BSSN formulation [200, 23], which is one of the most commonly used formulations in numerical relativity. Intrinsic numerical error from discretization served to perturb the ground state for both stable and unstable stars. It was found that unstable stars with negative binding energy would collapse and form a black hole, while ones with positive binding energy would suffer an excess of kinetic energy and disperse to infinity.
That these unstable stars would disperse, instead of simply expanding into some less compact stable solution, disagrees with the previous results of Ref. [196], and was subsequently further analyzed in [104] in spherical symmetry with an explicit perturbation (i.e., a Gaussian shell of particles, which increases the mass of the star around 0.1%). The spherically symmetric results corroborated the previous 3D calculations, suggesting that the slightly perturbed configurations of the unstable branch have three possible endstates: (i) collapse to BH, (ii) migration to a less dense stable solution, or (iii) dispersal to infinity, dependent on the sign of the binding energy.
Closely related is the work of Lai and Choptuik [142] studying BS critical behavior (discussed in Section 6.1). They tune perturbations of boson stars so that dynamically the solution approaches some particular unstable solution for some finite time. They then study evolutions that ultimately do not collapse to BH, so-called sub-critical solutions, and find that they do not disperse to infinity, instead oscillating about some less compact, stable star. They show results with increasingly distant outer boundary that suggest that this behavior is not a finite-boundary-related effect (reproduced in Figure 11). They use a different form of perturbation than Ref. [104], and, being only slightly subcritical, may be working in a regime with non-positive binding energy. However, it is interesting to consider that if indeed there are three distinct end-states, then one might expect critical behavior in the transition among the different pairings. Non-spherical perturbations of boson stars have been studied numerically in [14] with a 3D code to analyze the emitted gravitational waves.
Very long evolutions of a perturbed, slightly sub-critical, boson star with differing outer boundaries. The central magnitude of the scalar field is shown. At early times (t < 250 and the middle frame), the boson star demonstrates near-critical behavior with small-amplitude oscillations about an unstable solution. For late times (t > 250), the solution appears converged for the largest two outer boundaries and suggests that sub-critical boson stars are not dispersing. Instead, they execute large amplitude oscillations about low-density boson stars. Reprinted with permission from [142].
Much less is known about rotating BSs, which are more difficult to construct and to evolve because they are, at most, axisymmetric, not spherically symmetric. However, as mentioned in Section 3.5, they appear to have both stable and unstable branches [135] and are subject to an ergoregion instability at high rotation rates [44]. To our knowledge, no one has evolved rotating BS initial data. However, as discussed in the next section, simulations of BS binaries [167, 173] have found rotating boson stars as a result of merger.
The issue of formation of boson stars has been addressed in [198] by performing numerical evolutions of the EKG system with different initial Gaussian distributions describing unbound states (i.e., the kinetic energy is larger than the potential energy). Quite independent of the initial condition, the scalar field collapses and settles down to a bound state by ejecting some of the scalar energy during each bounce. The ejected scalar field carries away excess ever-decreasing amounts of kinetic energy, as the system becomes bounded. After a few free-fall times of the initial configuration, the scalar field has settled into a perturbed boson star on the stable branch. This process is the already mentioned gravitational cooling, and allows for the formation of compact soliton stars (boson stars for complex scalar fields and oscillatons for real scalar fields). Although these evolutions assumed spherical symmetry, which does not include important processes such as fragmentation or the formation of pancakes, they demonstrate the feasibility of the formation mechanism; clouds of scalar field will collapse under their own self-gravity while shedding excess kinetic energy. The results also confirm the importance of the mass term in the potential. By removing the massive term in the simulations, the field collapses, rebounds and completely disperses to infinity, and no compact object forms. The evolution of the scalar field with and without the massive term is displayed in Figure 12.
The evolution of r2 ρ (where ρ is the energy density of the complex scalar field) with massive field (left) and massless (right). In the massive case, much of the scalar field collapses and a perturbed boson star is formed at the center, settling down by gravitational cooling. In the massless case, the scalar field bounces through the origin and then disperses without forming any compact object. Reprinted with permission from [198]; copyright by APS.
4.2 Dynamics of binary boson stars
The dynamics of binary boson stars is sufficiently complicated that it generally requires numerical solutions. The necessary lack of symmetry and the resolution requirement dictated by the harmonic time dependence of the scalar field combine so that significant computational resources must be expended for such a study. However, boson stars serve as simple proxies for compact objects without the difficulties (shocks and surfaces) associated with perfect fluid stars, and, as such, binary BS systems have been studied in the two-body problem of general relativity. When sufficiently distant from each other, the precise structure of the star should be irrelevant as suggested by Damour’s “effacement theorem” [61].
First attempts at binary boson-star simulations assumed the Newtonian limit, since the SP system is simpler than the EKG one. Numerical evolutions of Newtonian binaries showed that in head-on collisions with small velocities, the stars merge forming a perturbed star [50]. With larger velocities, they demonstrate solitonic behavior by passing through each other, producing an interference pattern during the interaction but roughly retaining their original shapes afterwards [51]. In [50] it was also compute preliminary simulation of coalescing binaries, although the lack of resolution in these 3D simulations prevents of strong statements on these results. The head-on case was revisited in [26] with a 2D axisymmetric code. In particular, these evolutions show that final state will depend on the total energy of the system, that is, the addition of kinetic, gravitational and self-interaction energies. If the total energy is positive, the stars exhibit a solitonic behavior both for identical (see Figure 13) as for non-identical stars. When the total energy is negative, the gravitational force is the main driver of the dynamics of the system. This case produces a true collision, forming a single object with large perturbations, which slowly decays by gravitational cooling, as displayed in Figure 14.
Collision of identical boson stars with large kinetic energy in the Newtonian limit. The total energy (i.e., the addition of kinetic, gravitational and self-interaction) is positive and the collision displays solitonic behavior. Contrast this with the gravity-dominated collision displayed in Figure 14. Reprinted with permission from [26]; copyright by APS.
Collision of identical boson stars with small kinetic energy in the Newtonian limit. The total energy is dominated by the gravitational energy and is therefore negative. The collision leads to the formation of a single, gravitationally bound object, oscillating with large perturbations. This contrasts with the large kinetic energy case (and therefore positive total energy) displayed in Figure 13. Reprinted with permission from [26]; copyright by APS.
The first simulations of boson stars with full general relativity were reported in [12], where the gravitational waves were computed for a head-on collision. The general behavior is similar to the one displayed for the Newtonian limit; the stars attract each other through gravitational interaction and then merge to produce a largely perturbed boson star. However, in this case the merger of the binary was promptly followed by collapse to a black hole, an outcome not possible when working within Newtonian gravity instead of general relativity. Unfortunately, very little detail was given on the dynamics.
Much more elucidating was work in axisymmetry [141], in which head-on collisions of identical boson stars were studied in the context of critical collapse (discussed in Section 6.1) with general relativity. Stars with identical masses of M = 0.47 ≈ 0.75 Mmax were chosen, and so it is not surprising that for small initial momenta the stars merged together to form an unstable single star (i.e., its mass was larger than the maximum allowed mass, Mmax). The unstable hypermassive star subsequently collapsed to a black hole. However, for large initial momentum the stars passed through each other, displaying a form of solitonic behavior since the individual identities were recovered after the interaction. The stars showed a particular interference pattern during the overlap, much like that displayed in Figures 1 and 13.
Another study considered the very high speed, head-on collision of BSs [55]. Beginning with two identical boson stars boosted with Lorentz factors ranging as high as 4, the stars generally demonstrate solitonic behavior upon collision, as shown in the insets of Figure 18. This work is further discussed in Section 6.2.
The interaction of non-identical boson stars was studied in [174] using a 3D Cartesian code to simulate head-on collisions of stars initially at rest. It was found that, for a given separation, the merger of two stars would produce an unstable star that collapses to a black hole if the initial individual mass were M ≥ 0.26 ≈ 0.4 Mmax. For smaller masses, the resulting star would avoid gravitational collapse and its features would strongly depend on the initial configuration. The parameterization of the initial data was written as a superposition of the single boson-star solution ϕ0(r), located at different positions r1 and r2
Many different initial configurations are possible with this parameterization. The precise solution ϕ0 is unaffected by changing the direction of rotation (within in the complex plane isospace) via ϵ = ±1 or by a phase shift δ
When ϵ = −1, the Noether charge changes sign and the compact object is then known as an anti-boson star. Three particular binary cases were studied in detail: (i) identical boson stars (ϵ = 1, δ = 0), (ii) the pair in phase opposition (ϵ = 1, δ = π), and (iii) a boson-anti-boson pair (ϵ = −1, δ = 0). The trajectories of the centers of the stars are displayed in Figure 15, together with a simple estimate of the expected trajectory assuming Newtonian gravity. The figure makes clear that the merger depends strongly on the kind of pair considered, that is, on the interaction between the scalar fields.
The position of the center of one BS in a head-on binary as a function of time for (i) [B-B] identical BSs, (ii) [B-poB] opposite phase pair, and (iii) [B-aB] a boson-anti-boson pair. A simple argument is made, which qualitatively matches these numerical results, as discussed in Section 4.2. Also shown is the expected trajectory from a simple Newtonian two-body estimate. Reprinted with permission from [174]; copyright by APS.
A simple energy argument is made in [174] to understand the differing behavior. In the weak gravity limit when the stars are well separated, one can consider the local energy density between the two stars. In addition to the contribution due to each star separately, a remaining term Δ results from the interaction of the two stars and it is precisely this term that will depend on the parameters ϵ and δ. This term takes the simple form
where Δ0 is a positive definite quantity. One then observes that the identical pair will have an increased energy density Δ = +Δ0 resulting in a deeper (and more attractive) gravitational well between the stars. In contrast, the pair with opposite phases has a decreased energy density Δ = −Δ0 between them, resulting in a gravitational well less attractive than the area surrounding it resulting in repulsion. The boson-anti-boson pair has an interaction that is harmonic in time Δ = Δ0 cos (2ωt) and, therefore, sometimes positive and sometimes negative. However, if the time scale of interaction is not particularly fast, then the interaction averages to zero. Note that the boson-anti-boson pair trajectory is the closest to the simple Newtonian estimate. The qualitative behavior agrees very well with the numerical results.
The orbital case was later studied in [173]. This case is much more involved both from the computational point of view (i.e., there is less symmetry in the problem) and from the theoretical point of view, since for the final object to settle into a stationary, rotating boson star it must satisfy the additional quantization condition for the angular momentum of Eq. (71).
One simulation consisted of an identical pair each with individual mass M = 0.5, with small orbital angular momentum such that J ≤ N. In this case, the binary merges forming a rotating bar that oscillates for some time before ultimately splitting apart. This can be considered as a scattered interaction, which could not settle down to a stable boson star unless all the angular momentum was radiated.
In the case of boson-anti-boson pair, the total Noether charge is already trivial, and the final object resembles the structure of a rotating dipole. The pair in opposition of phase was not considered because of the repulsive effect from the interaction. The cases with very small angular momentum J ≪ N or with J ≤ N collapsed to a black hole soon after the merger. The trajectories for this latter case are displayed in Figure 16, indicating that the internal structure of the star is irrelevant (as per the effacement theorem [61]) until that the scalar fields overlap.
The position of the center of one BS within an orbiting binary as a function of time for the two cases: (i) [B-B] identical BSs and (ii) [B-poB] opposite phase pair. Notice that the orbits are essentially identical at early times (and large separations), but that they start to deviate from each other on closer approach. This is consistent with the internal structure of each member of the binary being irrelevant at large separations. Reprinted with permission from [173]; copyright by APS.
Other simulations of orbiting, identical binaries have been performed within the conformally flat approximation instead of full GR, which neglects gravitational waves (GW) [167]. Three different qualitative behaviors were found. For high angular momentum, the stars orbit for comparatively long times around each other. For intermediate values, the stars merged and formed a pulsating and rotating boson star. For low angular momentum, the merger produces a black hole. No evidence was found of the stars splitting apart after the merger.
5 Boson Stars in Astronomy
Scalar fields are often employed by astronomers and cosmologists in their efforts to model the Universe. Most models of inflation adopt a scalar field as the inflaton field, the vacuum energy of which drives the exponential inflation of the Universe. Dark energy also motivates many scalar field models, such as k-essence and phantom energy models. It is therefore not surprising that boson stars, as compact configurations of scalar field, are called upon to provide consequences similar to those observed.
5.1 As astrophysical stellar objects
We have already discussed a number of similarities between boson stars and models of neutron stars. Just as one can parameterize models of neutron stars by their central densities, one can consider a 1-parameter family of boson stars according to the central magnitude of the scalar field. Considering the mass as a function of this parameter, one finds the existence of a local maximum across which solutions transition from stable to unstable, just as is the case for neutron stars. Models of neutron stars can be constructed with different equations of state, whereas boson stars are constructed with differing scalar field potentials.
One difference of consequence concerns the stellar surface. Neutron stars of course have a surface at which the fluid density is discontinuous, as discussed for example in [99, 101]. In contrast, the scalar field that constitutes the boson star is smooth everywhere and lacks a particular surface. In its place, one generally defines a radius that encompasses some percentage (e.g. 99%) of the stellar mass. Such a difference could have observational consequences when matter accretes onto either type of star.
It is still an open question whether some of the stars already observed and interpreted as neutron stars could instead be astrophysical boson stars. In a similar fashion, it is not known whether many, if not all, of the stars we observe already have a bosonic component that has settled into the gravitational well of the star (see Section 3.6 for a discussion of fermionic-bosonic stars). The bosonic contribution may arise from exotic matter, which could appear at high densities inside the neutron star or from some sort of dark matter accretion. This possibility has gained popularity over the last years and there have been several attempts to constrain the properties of weakly interacting dark matter particles (WIMPs) by examining signatures related to their accretion and/or annihilation inside stars (for instance, see [137] and works cited in the introduction).
Recently, it was suggested that, due to the stronger gravitational field of neutron stars compared to other stars such as white dwarfs and main sequence stars, WIMPs will accrete more efficiently, leading to two different possibilities. If the dark matter is its own antiparticle, it will self-annihilate and heat the neutron star. This temperature increase could be observable in old stars, especially if they are close to the galactic center [137, 64]. If WIMPs do not self-annihilate, they will settle in the center of the star forming a sort of fermionic-bosonic star. The accretion of dark matter would then increase the star’s compactness until the star collapses [64].
Because of the similarities between boson stars and neutron stars, one finds that boson stars are often used in place of the other. This is especially so within numerical work because boson stars are easier to evolve than neutron star models. One can, for example compare the gravitational-wave signature of a boson-star merger with that of more conventional compact object binaries consisting of BHs and NSs (for a review of BH-NS binaries see [201]). At early times, the precise structure of the stars is irrelevant and the signatures are largely the same. However, for the late stages of merger, the relative phase of the boson stars determines the GW signature [174, 173].
Ref. [171] follows such work by considering the result of a collision between a BH and a boson star. In particular, they consider the problem as a perturbation of a black hole via scalar accretion and analyze the resulting gravitational-wave output. The hope is that observations of gravitational waves that are expected in a few years from aLIGO/Virgo will be able to distinguish the type of matter accreting onto a BH.
With the continued advancement in observation, both in the electromagnetic and gravitational spectra, perhaps soon we will have evidence for these questions. At the same time, further study of boson stars can help identify possible distinguishing observational effects in these bands. One example where knowledge is lacking is the interaction between boson stars with a magnetic field. Whereas a neutron star can source its own magnetic field and a neutral star can obtain an induced charge when moving with respect to a magnetic field, we are aware of no studies of the interaction of boson stars with a magnetic field.
5.2 Compact alternatives to black holes
As a localized scalar field configuration, a boson star can be constructed as a non-interacting compact object, as long as one does not include any explicit coupling to any electromagnetic or other fields. In that respect, it resembles a BH, although it lacks a horizon. Can observations of purported BHs be fully explained by massive boson stars? See Ref. [183] for a review of such observations.
Neutron stars also lack horizons, but, in contrast to a boson star, have a hard surface. A hard surface is important because one would expect accretion onto such a surface to have observable consequences. Can a boson star avoid such consequences? Yuan, Narayan and Rees consider the the viability of 10 M ⊙ boson stars as BH candidates in X-ray binaries [223]. They find that accreting gas collects not at the surface (which the star lacks), but instead at the center, which ultimately should lead to Type I X-ray bursts. Because these bursts are not observed, the case against boson stars as black hole mimickers is weakened (at least for BH candidates in X-ray binaries).
Ref. [105] considers a simplified model of accretion and searches for boson-star configurations that would mimic an accreting black hole. Although they find matches, they find that light deflection about a boson star will differ from the BH they mimic because of the lack of a photon sphere. Further work, studies the scalar field tails about boson stars and compares them to those of BHs [153]. If indeed a boson star collapses to a BH, then one could hope to observe the QNM of the massive scalar field, as described in [114].
Some of the strongest evidence for the existence of BHs is found at the center of most galaxies. The evidence suggests supermassive objects (of the order of millions of solar mass) occupying a small region (of order an astronomical unit) [32]. While definitive evidence for a BH horizon from conventional electromagnetic telescopes is perhaps just on the “horizon” [42], there are those who argue the viability of supermassive boson stars at galactic centers [214]. There could potentially be differences in the (electromagnetic) spectrum between a black hole and a boson star, but there is considerable freedom in adjusting the boson star potential to tweak the expected spectrum [103]. However, there are stringent constraints on BH alternatives to Sgr A* by the low luminosity in the near infrared [43]. In particular, the low luminosity implies a bound on the accretion rate assuming a hard surface radiating thermally and, therefore, the observational evidence favors a black hole because it lacks such a surface.
However, the observation of gravitational waves from such objects may be able to distinguish BHs from BSs [28]. Such a test would occur in the bandwidth for a space-based observatory such as the beleaguered LISA mission. Because BSs allow for orbits within what would otherwise be a black-hole event horizon, geodesics will exhibit extreme pericenter precession resulting in potentially distinguishable gravitational radiation [128]. In any case, observations of supermassive objects at the centers of galaxies can be used to constrain the scalar field parameters of possible mimickers [17].
There are other possible BH mimickers, and a popular recent one is the gravastar [158]. Common among all these alternatives, and most significantly, is the lack of an event horizon. Both gravastars and BSs undergo an ergoregion instability for high spin (J/(GM2) > 0.4) [44]. As mentioned above for BSs, gravitational waves may similarly be able to distinguish gravastars from BHs [175].
5.3 As origin of dark matter
Studies of stellar orbits within various galaxies produce rotation curves, which indicate galactic mass within the radius of the particular orbit. The discovery that these curves remain flat at large radius suggests the existence of a large halo of massive, yet dark, matter that holds the galaxy together despite its large rotation. However, what precise form of matter could fulfill the observational constraints is still very much unclear. Scalar fields are an often used tool in the cosmologist’s toolkit, but one cannot have a regular, static configuration of scalar field to serve as the halo [178] (see [69] as discussed in Section 6.3 for a discussion of rotating boson stars with embedded, rotating BH solutions). Instead, galactic scale boson stars are one possible candidate.
Boson stars can be matched onto the observational constraints for galactic dark matter halos [145, 199]. However, multi-state boson stars that superpose various boson-star solutions (e.g., an unexcited solution with an excited solution) can perhaps find better fits to the constraints [215]. Boson stars at the galactic scale may not exhibit general relativistic effects and can be effectively considered as Bose-Einstein condensates (BEC) with angular momentum [185].
The solitonic nature of boson stars (see Figure 1) lends itself naturally to the wonderful observation of dark matter in the Bullet Cluster [146]. Ref. [144] attempts to determine a minimum galactic mass from such a match.
Interestingly, Ref. [19] foregoes boson stars and instead looks for quasi-stationary scalar solutions about a Schwarzschild black hole that could conceivably survive for cosmological times. Another approach is to use scalar fields for both the dark matter halo and the supermassive, central object. Ref. [8] looks for such a match, but finds no suitable solutions. Quite a number of more exotic models viably fit within current constraints, including those using Q-balls [71].
6 Boson Stars in Mathematical Relativity
Although the experimental foundation for the existence of boson stars is completely lacking, on the theoretical and mathematical front, boson stars are well studied. Recent work includes a mathematical approach in terms of large and small data [87], followed up by studying singularity formation [151] and uniqueness [88, 150] for a certain boson star equation. In Ref. [48], they study radial solutions of the semi-relativistic Hartree type equations in terms of global well-posedness. Ref. [30] demonstrates stationarity of time periodic scalar field solutions.
Beyond just existence, however, boson stars are often employed mathematically to study dynamics. Here, we concentrate on a few of these topics that have attracted recent interest.
6.1 Black hole critical behavior
If one considers some initial distribution of energy and watches it evolve, generally one arrives at one of three states. If the energy is sufficiently weak in terms of its gravity, the energy might end up dispersing to larger and large distances. However, if the energy is instead quite large, then perhaps it will concentrate until a black hole is formed. Or, if the form of the energy supports it, some of the energy will condense into a stationary state.
In his seminal work [52], Choptuik considers a real, massless scalar field and numerically evolves various initial configurations, finding either dispersion or black-hole formation. By parameterizing these initial configurations, say by the amplitude of an initial pulse p, and by tuning this parameter, he was able to study the threshold for black-hole formation at which he found fascinating black-hole critical behavior. In particular, his numerical work suggested that continued tuning could produce as small a black hole as one wished. This behavior is analogous to a phase transition in which the black-hole mass serves as an order parameter. Similar to phase transitions, one can categorize two types of transition that distinguish between whether the black-hole mass varies continuously (Type II) or discontinuously (Type I). For Choptuik’s work with a massless field, the transition is therefore of Type II because the black-hole mass varies from zero continuously to infinitesimal values.
Subsequent work has since established that this critical behavior can be considered as occurring in the neighborhood of a separatrix between the basins of attraction of the two end states. For p = p*, the system is precisely critical and remains on the (unstable) separatrix. Similarly other models find such threshold behavior occurring between a stationary state and black-hole formation. Critical behavior about stationary solutions necessarily involve black-hole formation “turning-on” at finite mass, and is therefore categorized as Type I critical behavior.
The critical surface, therefore, appears as a co-dimension 1 surface, which evolutions increasingly approach as one tunes the parameter p. The distance from criticality |p − p*| serves as a measure of the extent to which a particular initial configuration has excited the unstable mode that drives solutions away from this surface. For Type II critical behavior, the mass of the resulting black-hole mass scales as a power law in this distance, whereas for Type I critical behavior, it is the survival time of the critical solution that scales as a power law. See [100] for a recent review.
We have seen that boson stars represent stationary solutions of Einstein’s equations and, thus, one would correctly guess that they may occur within Type I black-hole critical behavior. To look for such behavior, Hawley and Choptuik [109] begin their evolutions with boson-star solutions and then perturb them both dynamically and gravitationally. They, therefore, included in their evolutionary system a distinct, free, massless, real scalar field which couples to the boson star purely through its gravity.
The initial data, therefore, consisted of a boson star surrounded by a distant, surrounding shell of real scalar field parametrized by the amplitude of the shell. For small perturbations, the boson star oscillated about an unstable boson star before settling into a low mass, stable solution (see Figure 17). For large perturbations, the real scalar field serves to compress the initial star and, after a period of oscillating about an unstable boson star, the complex field collapses to a black hole. By tuning the initial perturbation, they find a longer and longer lived unstable boson star, which serves as the critical solution (see Figure 11). The survival time τ obeys a power law in terms of the distance from criticality |p − p*|
where γ is a real constant that depends on the characteristic instability rate of the particular unstable boson star approached in the critical regime.
Evolution of a boson star (solid line) perturbed by a shell of scalar field (dashed line). Shown is the mass density ∂M/∂r for each contribution. By t ≈ 100 the real scalar field pulse has departed the central region and perturbed the boson star into an unstable, compact configuration. Contrast the t = 0 frame with that of t = 97.5 and note the increase in compaction. This unstable BS survives until t ≈ 500 only because the initial perturbation has been tuned to one part in 1015 and indicates Type I critical behavior. Reprinted with permission from [142].
One can also consider these BSs in axisymmetry in which non-spherically symmetric modes could potentially become important. A first step in this direction studied spherically symmetric BSs within conformally flat gravity (which does not allow for gravitational waves) in axisymmetry [187]. Later, better resolution using adaptive mesh refinement within full general relativity was achieved by [141, 142], which upheld the results found within spherical symmetry. This work thus suggests that there are either no additional, unstable, axisymmetric modes or that such unstable modes are extremely slowly growing.
A very different type of critical behavior was also investigated by Lai [141]. By boosting identical boson stars toward each other and adjusting their initial momenta, he was able to tune to the threshold for black-hole formation. At the threshold, he found that the time till black-hole formation scaled consistent with Type I critical behavior and conjectured that the critical solution was itself an unstable boson star. This is one of the few fully nonlinear critical searches in less symmetry than spherical symmetry, and the first of Type I behavior in less symmetry. A related study colliding neutron stars instead of boson stars similarly finds Type I critical behavior [124] and subsequently confirmed by [127].
The gauged stars discussed in Section 3.9 also serve as critical solutions in spherical symmetry [53, 54, 166].
6.2 Hoop conjecture
An interesting use of boson stars was made by Choptuik and Pretorius [55]. They sought to answer classically whether the ultra-relativistic collision of two particles results in black-hole formation. Such a question clearly has relevance to hopes of producing black holes at the LHC (see, for example, [143, 177]). Guidance on this question is provided by Thorne’s Hoop Conjecture [213], which suggests that a black hole is formed if one squeezes energy into some spherical space of dimension less than the Schwarzschild radius for that energy.
They, therefore, numerically collide boson stars head-on at relativistic energies to study blackhole formation from just such dynamical “squeezing”. Here, the nature of boson stars is largely irrelevant as they serve as simple bundles of energy that can be accelerated (see Figure 18). However, unlike using boosted black-hole solutions, the choice of boson stars avoids any type of bias or predisposition to formation of a black hole. In addition, a number of previous studies of boson star head-on collisions showed interesting interference effects at energies below the threshold for black-hole formation [49, 51, 141, 167]. Indeed, it has been proposed that such an interference pattern could be evidence for the bosonic nature of dark matter because of evidence that an ideal fluid fails to produce such a pattern [95].
Evolutions of the head-on collisions of identical boson stars boosted toward each other with initial Lorentz factors γ as indicated. Time flows downward within each column and the top edge displays the axis of symmetry. The color-scale indicates the value of |ϕ|. In the middle frames one sees the interference pattern characteristic of high kinetic energy BS collisions (as mentioned in Figure 1). In the last column on the right, the collision produces a BH with apparent horizon indicated by the black oval in the third frame. Reprinted with permission from [55]; copyright by APS.
Choptuik and Pretorius [55] find that indeed black-hole formation occurs at energies below that estimated by the Hoop Conjecture. This result is only a classical result consistent with the conjecture, but if it had not held, then there would have been no reason to expect a quantum theory to be consistent with it.
6.3 Other dimensions
Much work has been invested recently in considering physics in other dimensions. Motivation comes from various ideas including string theory (more dimensions) such as the AdS/CFT correspondence and holography (one fewer dimensions) [156, 159, 181]. Another source of motivation comes from the fact that higher dimensional black holes can have very different properties than those in three spatial dimensions [75]. Perhaps BSs will similarly display novel properties in other dimensions.
In lower dimensional AdS (2+1) spacetimes, early work in 1998 studied exact solutions of boson stars [191, 67, 192]. Higher dimensional scenarios were apparently first considered qualitatively a few years later in the context of brane world models [205]. This discussion was followed with a detailed analysis of the 3, 4, and 5 dimensional AdS solutions [11].
More recently, Ref. [84] considers oscillatons in higher dimensions and measure the scalar mass loss rate for dimensions 3, 4, and 5. They extend this work considering inflationary spacetimes [83].
The axisymmetric rotating BSs discussed in Section 3.5 satisfy a coupled set of nonlinear, elliptic PDEs in two dimensions. One might, therefore, suspect that adding another dimensions will only make things more difficult. As it turns out, however, moving to four spatial dimensions provides for another angular momentum, independent of the one along the z-direction (for example). Each of these angular momenta are associated with their own orthogonal plane of rotation. And so if one chooses solutions with equal magnitudes for each of these momenta, the solutions depend on only a single radial coordinate. This choice results in the remarkable simplification that one need only solve ODEs to find rotating solutions [138].
In [108], they extend this idea by assuming an ansatz for two complex scalar fields with equal magnitudes of angular momentum in the two independent directions. Letting the complex doublet be denoted by Φ, the ansatz takes the form
in terms of the two angular coordinates φ1 and φ2. One observes that the BS (i) retains a profile ϕ(r), (ii) possesses harmonic time dependence, and (iii) maintains single-valuedness in the two angles (the ansatz assumes a rotational quantum number of one). They find solutions that are both globally regular and asymptotically flat but these solutions appear only stable with weak gravitational coupling [108].
The work of [69] makes ingenious use of this 5D ansatz to construct rotating black holes with only a single Killing vector. They set the potential of [108] to zero so that the scalar fields are massless and they add a (negative) cosmological constant to work in anti-de Sitter (AdS). They find solutions for rotating black holes in 5D AdS that correspond to a bar mode for rotating neutron stars in 3D (see also [202] for a numerical evolution of a black hole in higher dimensions, which demonstrates such bar formation). One might expect such a non-symmetric black hole to settle into a more symmetric state via the emission of gravitational waves. However, AdS provides for an essentially reflecting boundary in which the black hole can be in equilibrium. The distortion of the higher dimensional black hole also has a correspondence with the discrete values of the angular momentum of the corresponding boson star. For higher values of the rotational quantum number, the black hole develops multiple “lobes” about its center.
These solutions are extended to arbitrary odd-dimensional AdS spacetimes in [206]. Finding the solutions perturbatively, they explicitly show that these solutions approach (i) the boson star and (ii) the Myers-Perry black-hole solutions in AdS [170] in different limits. See [75] for a review of black holes in higher dimensions.
The same authors of [69] also report on the existence of geons in 3+1 AdS “which can be viewed as gravitational analogs of boson stars” [70] (recall that boson stars themselves arose from Wheeler’s desire to construct local electrovacuum solutions). These bundles of gravitational energy are stable to first order due to the confining boundary condition adopted with AdS. However, these geons and the black-hole solutions above [69] are unstable at higher order because of the turbulent instability reported in [31].
Ref. [21] also studies black-hole solutions in 5D AdS. They find solutions for black holes with scalar hair that resemble a boson star with a BH in its center. See Ref. [92] for a review of charged scalar solitons in AdS.
7 Final Remarks
Boson stars have a long history as candidates for all manner of phenomena, from fundamental particle, to galactic dark matter. A huge variety of solutions have been found and their dynamics studied. Mathematically, BS are fascinating soliton-like solutions. Astrophysically, they represent possible explanations of black-hole candidates and dark matter, with observations constraining BS properties.
Further constraints appear to be right around the corner in a few directions. The LHC is rapidly narrowing the possible mass range for a Higgs particle (the quantized version of a fundamental scalar field), and some hold hope that black holes might be produced that would indicate the existence of higher dimensions. COGENT, Pamela, and others are finding intriguing (and frustratingly contradictory) clues about the true nature of dark matter. And Planck and JWST, if it can overcome its funding and budgetary problems, promise to further refine our view of the cosmos and the role of scalar fields within. Advanced LIGO will be complete in a few years and the future of space-based GW telescopes such as LISA is currently being determined. GW observations will be ground-breaking on so many fronts, but could potentially help distinguish BSs from neutron stars or black holes.
Perhaps future work on boson stars will be experimental, if fundamental scalar fields are observed, or if evidence arises indicating the boson stars uniquely fit galactic dark matter. But regardless of any experimental results found by these remarkable experiments, there will always be regimes unexplored by experiments where boson stars will find a natural home.
References
Adam, C., Grandi, N., Klimas, P., Sánchez-Guillén, J. and Wereszczyński, A., “Compact boson stars in K field theories”, Gen. Relativ. Gravit., 42, 2663–2701, (2010). [DOI], [ADS], [arXiv:0908.0218 [hep-th]]. (Cited on page 17.)
Agnihotri, P., Schaffner-Bielich, J. and Mishustin, I.N., “Boson stars with repulsive self-interactions”, Phys. Rev. D, 79, 084033, (2009). [DOI], [ADS], [arXiv:0812.2770]. (Cited on page 15.)
Akhoury, R. and Gauthier, C.S., “Galactic Halos and Black Holes in Non-Canonical Scalar Field Theories”, arXiv, e-print, (2008). [ADS], [arXiv:0804.3437 [hep-th]]. (Cited on page 17.)
Alcubierre, M., Introduction to 3+1 Numerical Relativity, International Series of Monographs on Physics, 140, (Oxford University Press, Oxford; New York, 2008). (Cited on page 10.)
Alcubierre, M., Becerril, R., Guzmán, F.S., Matos, T., Núñez, D. and Ureña-López, L.A., “Numerical studies of Φ2-oscillatons”, Class. Quantum Grav., 20, 2883–2903, (2003). [DOI], [ADS], [arXiv:gr-qc/0301105]. (Cited on pages 20, 21, and 22.)
Alcubierre, M., Degollado, J.C., Núñez, D., Ruiz, M. and Salgado, M., “Dynamic transition to spontaneous scalarization in boson stars”, Phys. Rev. D, 81, 124018, (2010). [DOI], [arXiv:1003.4767 [gr-qc]]. (Cited on page 26.)
Alic, D., Theoretical issues in Numerical Relativity simulations, Ph.D. thesis, (Universitat de les Illes Balears, Palma, 2009). URL (accessed 3 February 2012): http://hdl.handle.net/10803/9438. (Cited on page 25.)
Amaro-Seoane, P., Barranco, J., Bernal, A. and Rezzolla, L., “Constraining scalar fields with stellar kinematics and collisional dark matter”, J. Cosmol. Astropart. Phys., 11, 2, (2010). [DOI], [ADS], [arXiv:1009.0019 [astro-ph.CO]]. (Cited on pages 15, 16, and 41.)
Arnowitt, R., Deser, S. and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, pp. 227–265, (Wiley, New York; London, 1962). [DOI], [ADS], [arXiv:gr-qc/0405109]. (Cited on page 10.)
Arodz, H., Karkowski, J. and Świerczyński, Z., “Spinning Q-balls in the complex signum-Gordon model”, Phys. Rev. D, 80, 067702, (2009). [DOI], [ADS], [arXiv:0907.2801 [hep-th]]. (Cited on page 17.)
Astefanesei, D. and Radu, E., “Boson stars with negative cosmological constant”, Nucl. Phys. B, 665, 594–622, (2003). [DOI], [arXiv:gr-qc/0309131]. (Cited on page 45.)
Balakrishna, J., A numerical study of boson stars: Einstein equations with a matter source, Ph.D. thesis, (Washington University, St. Louis, 1999). [ADS], [arXiv:gr-qc/9906110]. (Cited on page 34.)
Balakrishna, J., Bondarescu, R., Daues, G. and Bondarescu, M., “Numerical simulations of oscillating soliton stars: Excited states in spherical symmetry and ground state evolutions in 3D”, Phys. Rev. D, 77, 024028, (2008). [DOI], [ADS], [arXiv:0710.4131 [gr-qc]]. (Cited on page 21.)
Balakrishna, J., Bondarescu, R., Daues, G., Guzmán, F.S. and Seidel, E., “Evolution of 3D Boson Stars with Waveform Extraction”, Class. Quantum Grav., 23, 2631–2652, (2006). [DOI], [ADS], [arXiv:gr-qc/602078]. (Cited on page 32.)
Balakrishna, J., Seidel, E. and Suen, W.-M., “Dynamical evolution of boson stars. II. Excited states and self-interacting fields”, Phys. Rev. D, 58, 104004, (1998). [DOI], [ADS], [arXiv:gr-qc/9712064]. (Cited on pages 30 and 31.)
Bao, W. and Dong, X., “Numerical methods for computing ground states and dynamics of nonlinear relativistic Hartree equation for boson stars”, J. Comput. Phys., 230, 5449–5469, (2011). [DOI], [ADS]. (Cited on page 18.)
Barranco, J. and Bernal, A., “Constraining scalar field properties with boson stars as black hole mimickers”, in Ureña-López, L.A., Morales-Técotl, H.A., Linares-Romero, R., Santos-Rodríguez, E. and Estrada-Jiménez, S., eds., VIII Workshop of the Gravitation and Mathematical Physics Division of the Mexican Physical Society, Tuxtla Gutiérrez, Chiapas, Mexico, 22–26 November 2010, AIP Confernce Proceedings, 1396, pp. 171–175, (American Institute of Physics, Melville, NY, 2011). [DOI], [arXiv:1108.1208 [astro-ph.CO]]. (Cited on page 40.)
Barranco, J. and Bernal, A., “Self-gravitating system made of axions”, Phys. Rev. D, 83, 043525, (2011). [DOI], [ADS], [arXiv:1001.1769 [astro-ph.CO]]. (Cited on page 15.)
Barranco, J., Bernal, A., Degollado, J.C., Diez-Tejedor, A., Megevand, M., Alcubierre, M., Núñez, D. and Sarbach, O., “Are black holes a serious threat to scalar field dark matter models?”, Phys. Rev. D, 84, 083008, (2011). [DOI], [arXiv:1108.0931 [gr-qc]]. (Cited on page 41.)
Bartnik, R. and Mckinnon, J., “Particlelike Solutions of the Einstein-Yang-Mills Equations”, Phys. Rev. Lett., 61, 141–144, (1988). [DOI]. (Cited on page 27.)
Basu, P., Bhattacharya, J., Bhattacharyya, S., Loganayagam, R., Minwalla, S. and Umesh, V., “Small hairy black holes in global AdS spacetime”, J. High Energy Phys., 2010(10), 045, (2010).[DOI], [ADS], [arXiv:1003.3232 [hep-th]]. (Cited on page 46.)
Battye, R.A. and Sutcliffe, P.M., “Q-ball dynamics”, Nucl. Phys. B, 590, 329–363, (2000). [DOI], [ADS], [arXiv:hep-th/0003252]. (Cited on page 17.)
Baumgarte, T.W. and Shapiro, S.L., “Numerical integration of Einstein’s field equations”, Phys. Rev. D, 59, 024007, (1998). [DOI], [ADS], [arXiv:gr-qc/9810065]. (Cited on page 31.)
Baumgarte, T.W. and Shapiro, S.L., Numerical Relativity: Solving Einstein’s Equations on the Computer, (Cambridge University Press, Cambridge; New York, 2010). [Google Books]. (Cited on page 10.)
Bernal, A., Barranco, J., Alic, D. and Palenzuela, C., “Multistate boson stars”, Phys. Rev. D, 81, 044031, (2010). [DOI], [ADS], [arXiv:0908.2435 [gr-qc]]. (Cited on pages 25 and 26.)
Bernal, A. and Guzmán, F.S., “Scalar field dark matter: Head-on interaction between two structures”, Phys. Rev. D, 74, 103002, (2006). [DOI], [ADS], [arXiv:astro-ph/0610682]. (Cited on pages 34 and 35.)
Bernal, A. and Guzmán, F.S., “Scalar field dark matter: Nonspherical collapse and late-time behavior”, Phys. Rev. D, 74, 063504, (2006). [DOI], [ADS], [arXiv:astro-ph/0608523]. (Cited on page 18.)
Berti, E. and Cardoso, V., “Supermassive Black Holes or Boson Stars? Hair Counting with Gravitational Wave Detectors”, Int. J. Mod. Phys. D, 15, 2209–2216, (2006). [DOI], [ADS], [arXiv:gr-qc/0605101]. (Cited on page 40.)
Bhatt, J.R. and Sreekanth, V., “Boson stars: Chemical potential and quark condensates”, arXiv, e-print, (2009). [ADS], [arXiv:0910.1972 [hep-ph]]. (Cited on page 17.)
Bičák, J., Scholtz, M. and Tod, P., “On asymptotically flat solutions of Einstein’s equations periodic in time II. Spacetimes with scalar-field sources”, Class. Quantum Grav., 27, 175011, (2010). [DOI], [arXiv:1008.0248 [gr-qc]]. (Cited on page 42.)
Bizoń, P. and Rostworowski, A., “On weakly turbulent instability of anti-de Sitter space”, Phys. Rev. Lett., 107, 031102, (2011). [DOI], [arXiv:1104.3702 [gr-qc]]. (Cited on page 46.)
Boehle, A., Ghez, A., Schoedel, R., Yelda, S. and Meyer, L., “New Orbital Analysis of Stars at the Galactic Center Using Speckle Holography”, in AAS 219th Meeting, Austin, Texas, 8–12 January 2012, Bull. Am. Astron. Soc., 44, 252.01, (American Astronomical Society, Washington, DC, 2012). [ADS]. (Cited on page 40.)
Bogolyubskiĭ, I.L. and Makhan’kov, V.G., “Dynamics of spherically symmetrical pulsons of large amplitude”, JETP Lett., 25, 107–110, (1977). [ADS]. (Cited on page 21.)
Bona, C., Palenzuela, C. and Bona, C., Elements of Numerical Relativity and Relativistic Hydrodynamics: From Einstein’s Equations to Astrophysical Simulations, Lecture Notes in Physics, 783, (Springer, Berlin; New York, 2009), 2nd edition. [Google Books]. (Cited on page 10.)
Brady, P.R., Choptuik, M.W., Gundlach, C. and Neilsen, D.W., “Black-hole threshold solutions in stiff fluid collapse”, Class. Quantum Grav., 19, 6359–6376, (2002). [DOI], [arXiv:gr-qc/0207096]. (Cited on page 7.)
Brihaye, Y., Caebergs, T. and Delsate, T., “Charged-spinning-gravitating Q-balls”, arXiv, e-print, (2009). [arXiv:0907.0913 [gr-qc]]. (Cited on page 20.)
Brihaye, Y., Caebergs, T., Hartmann, B. and Minkov, M., “Symmetry breaking in (gravitating) scalar field models describing interacting boson stars and Q-balls”, Phys. Rev. D, 80, 064014, (2009). [DOI], [ADS], [arXiv:0903.5419 [gr-qc]]. (Cited on page 26.)
Brihaye, Y. and Hartmann, B., “Angularly excited and interacting boson stars and Q balls”, Phys. Rev. D, 79, 064013, (2009). [DOI], [ADS], [arXiv:0812.3968 [hep-ph]]. (Cited on page 26.)
Brihaye, Y., Hartmann, B. and Radu, E., “Boson stars in SU(2) Yang-Mills-scalar field theories”, Phys. Lett. B, 607, 17–26, (2005). [DOI], [arXiv:hep-th/0411207 [hep-th]]. (Cited on page 27.)
Brihaye, Y. and Verbin, Y., “Spherical Structures in Conformal Gravity and its Scalar-Tensor Extension”, Phys. Rev. D, 80, 124048, (2009). [DOI], [arXiv:0907.1951 [gr-qc]]. (Cited on page 26.)
Brihaye, Y. and Verbin, Y., “Spherical Non-Abelian Solutions in Conformal Gravity”, Phys. Rev. D, 81, 044041, (2010). [DOI], [arXiv:0910.0973 [gr-qc]]. (Cited on pages 26 and 27.)
Broderick, A.E., Loeb, A. and Reid, M.J., “Localizing Sagittarius A* and M87 on Microarcsecond Scales with Millimeter Very Long Baseline Interferometry”, Astrophys. J., 735, 57, (2011). [DOI], [ADS], [arXiv:1104.3146 [astro-ph.HE]]. (Cited on page 40.)
Broderick, A.E. and Narayan, R., “On the nature of the compact dark mass at the galactic center”, Astrophys. J., 638, L21–L24, (2006). [DOI], [arXiv:astro-ph/0512211 [astro-ph]]. (Cited on page 40.)
Cardoso, V., Pani, P., Cadoni, M. and Cavaglià, M., “Ergoregion instability of ultracompact astro-physical objects”, Phys. Rev. D, 77, 124044, (2008). [DOI], [ADS], [arXiv:0709.0532 [gr-qc]]. (Cited on pages 23, 29, 32, and 41.)
Chavanis, P.-H., “Mass-radius relation of Newtonian self-gravitating Bose-Einstein condensates with short-range interactions. I. Analytical results”, Phys. Rev. D, 84, 043531, (2011). [DOI], [ADS], [arXiv:1103.2050 [astro-ph.CO]]. (Cited on page 18.)
Chavanis, P.-H., “Growth of perturbations in an expanding universe with Bose-Einstein condensate darkmatter”, Astron. Astrophys., 537, A127, (2012). [DOI], [ADS], [arXiv:1103.2698 [astro-ph.CO]]. (Cited on page 18.)
Chavanis, P.-H. and Harko, T., “Bose-Einstein Condensate general relativistic stars”, arXiv, e-print, (2011). [ADS], [arXiv:1108.3986 [astro-ph.SR]]. (Cited on page 18.)
Cho, Y., Ozawa, T., Sasaki, H. and Shim, Y., “Remarks on the semirelativistic Hartree equations”, Discrete Contin. Dyn. Syst. A, 23, 1277–1294, (2009). [DOI]. (Cited on page 42.)
Choi, D., Lai, C.W., Choptuik, M.W., Hirschmann, E.W., Liebling, S.L. and Pretorius, F., “Dynamics of Axisymmetric (Head-on) Boson Star Collisions”, in preparation, (2010). Online version (accessed 3 February 2012): http://bh0.physics.ubc.ca/Group/PapersInProgress.html. (Cited on pages 8 and 44.)
Choi, D.-I., Numerical Studies of Nonlinear Schrödinger and Klein-Gordon Systems: Techniques and Applications, Ph.D. thesis, (The University of Texas, Austin, 1998). [ADS]. Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on pages 33 and 34.)
Choi, D.-I., “Collision of gravitationally bound Bose-Einstein condensates”, Phys. Rev. A, 66, 063609, (2002). [DOI], [ADS]. (Cited on pages 34 and 44.)
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70, 9–12, (1993). [DOI], [ADS]. (Cited on page 42.)
Choptuik, M.W., Chmaj, T. and Bizoń, P., “Critical Behavior in Gravitational Collapse of a Yang-Mills Field”, Phys. Rev. Lett., 77, 424–427, (1996). [DOI], [arXiv:gr-qc/9603051]. (Cited on page 44.)
Choptuik, M.W., Hirschmann, E.W. and Marsa, R.L., “New critical behavior in Einstein-Yang-Mills collapse”, Phys. Rev. D, 60, 124011, (1999). [DOI], [arXiv:gr-qc/9903081]. (Cited on page 44.)
Choptuik, M.W. and Pretorius, F., “Ultrarelativistic Particle Collisions”, Phys. Rev. Lett., 104, 111101, (2010). [DOI], [arXiv:0908.1780 [gr-qc]]. (Cited on pages 35 and 44.)
Coleman, S.R., “Q Balls”, Nucl. Phys. B, 262, 263, (1985). [DOI]. (Cited on page 17.)
Colpi, M., Shapiro, S.L. and Wasserman, I., “Boson stars: Gravitational equilibria of self-interacting scalar fields”, Phys. Rev. Lett., 57, 2485–2488, (1986). [DOI], [ADS]. (Cited on pages 15 and 16.)
Contaldi, C.R., Wiseman, T. and Withers, B., “TeVeS gets caught on caustics”, Phys. Rev. D, 78, 044034, (2008). [DOI], [ADS], [arXiv:0802.1215 [gr-qc]]. (Cited on page 27.)
Cook, G.B., “Initial Data for Numerical Relativity”, Living Rev. Relativity, 3, lrr-2000-5, (2000). [gr-qc/0007085]. URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2000-5. (Cited on page 14.)
Cook, G.B., Shapiro, S.L. and Teukolsky, S.A., “Rapidly rotating neutron stars in general relativity: Realistic equations of state”, Astrophys. J., 424, 823–845, (1994). [DOI], [ADS]. (Cited on pages 28 and 29.)
Damour, T., “The problem of motion in Newtonian and Einsteinian gravity”, in Hawking, S.W. and Israel, W., eds., Three Hundred Years of Gravitation, pp. 128–198, (Cambridge University Press, Cambridge; New York, 1987). [ADS]. (Cited on pages 33 and 37.)
Damour, T. and Esposito-Farèse, G., “Tensor-scalar gravity and binary-pulsar experiments”, Phys. Rev. D, 54, 1474–1491, (1996). [DOI], [arXiv:gr-qc/9602056]. (Cited on page 26.)
Dariescu, C. and Dariescu, M.-A., “Boson Nebulae Charge”, Chinese Phys. Lett., 27, 011101, (2010). [DOI], [ADS]. (Cited on page 19.)
de Lavallaz, A. and Fairbairn, M., “Neutron stars as dark matter probes”, Phys. Rev. D, 81, 123521, (2010). [DOI]. (Cited on page 39.)
de Sousa, C.M.G., Silveira, V. and Fang, L.Z., “Slowly Rotating Boson-Fermion Star”, Int. J. Mod. Phys. D, 10, 881–892, (2001). [DOI], [ADS], [arXiv:gr-qc/0012020]. (Cited on page 25.)
de Sousa, C.M.G., Tomazelli, J.L. and Silveira, V., “Model for stars of interacting bosons and fermions”, Phys. Rev. D, 58, 123003, (1998). [DOI], [ADS], [arXiv:gr-qc/9507043]. (Cited on page 23.)
Degura, Y., Sakamoto, K. and Shiraishi, K., “Black holes with scalar hair in (2+1)-dimensions”, Grav. Cosmol., 7, 153–158, (2001). [arXiv:gr-qc/9805011 [gr-qc]]. (Cited on page 45.)
Derrick, G.H., “Comments on nonlinear wave equations as models for elementary particles”, J. Math. Phys., 5, 1252–254, (1964). [DOI]. (Cited on page 6.)
Dias, O.J.C., Horowitz, G.T. and Santos, J.E., “Black holes with only one Killing field”, arXiv, e-print, (2011). [arXiv:1105.4167 [Black holes, Killing field]]. (Cited on pages 23, 41, 45, and 46.)
Dias, O.J.C., Horowitz, G.T. and Santos, J.E., “Gravitational Turbulent Instability of Anti-de Sitter Space”, arXiv, e-print, (2011). [arXiv:1109.1825 [hep-th]]. (Cited on pages 27 and 45.)
Doddato, F. and McDonald, J., “New Q-ball Solutions in Gauge-Mediation, Affleck-Dine Baryogenesis and Gravitino Dark Matter”, arXiv, e-print, (2011). [arXiv:1111.2305 [hep-ph]]. (Cited on page 41.)
Dzhunushaliev, V., Folomeev, V., Myrzakulov, R. and Singleton, D., “Non-singular solutions to Einstein-Klein-Gordon equations with a phantom scalar field”, J. High Energy Phys., 2008(07), 094, (2008). [DOI], [ADS], [arXiv:0805.3211 [gr-qc]]. (Cited on page 17.)
Dzhunushaliev, V., Folomeev, V. and Singleton, D., “Chameleon stars”, Phys. Rev. D, 84, 084025, (2011). [DOI], [arXiv:1106.1267 [astro-ph.SR]]. (Cited on page 25.)
Dzhunushaliev, V., Myrzakulov, K. and Myrzakulov, R., “Boson Stars from a Gauge Condensate”, Mod. Phys. Lett. A, 22, 273–81, (2007). [DOI], [ADS], [arXiv:gr-qc/0604110]. (Cited on page 27.)
Emparan, R. and Reall, H.S., “Black Holes in Higher Dimensions”, Living Rev. Relativity, 11, lrr-2008-6, (2008). URL (accessed 1 February 2012): http://rwww.livingreviews.org/lrr-2008-6. (Cited on page 45.)
Eto, M., Hashimoto, K., Iida, H. and Miwa, A., “Chiral Magnetic Effect from Q-balls”, arXiv, e-print, (2010). [arXiv:1012.3264 [hep-ph]]. (Cited on page 20.)
Famaey, B. and McGaugh, S., “Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions”, Living Rev. Relativity, 15, lrr-2012-, (2012). [arXiv:1112.3960 [astro-ph.CO]]. URL (accessed 7 May 2012): http://www.livingreviews.org. (Cited on page 27.)
Faraoni, V., “Correspondence between a scalar field and an effective perfect fluid”, Phys. Rev. D, 85, 024040, (2012). [DOI], [arXiv:1201.1448 [gr-qc]]. (Cited on page 7.)
Fodor, G., Forgáacs, P., Horváath, Z. and Lukacs, A., “Small amplitude quasi-breathers and oscillons”, Phys. Rev. D, 78, 025003, (2008). [DOI], [arXiv:0802.3525 [hep-th]]. (Cited on page 21.)
Fodor, G., Forgáacs, P., Horváath, Z. and Mezei, M., “Computation of the radiation amplitude of oscillons”, Phys. Rev. D, 79, 065002, (2009). [DOI], [arXiv:0812.1919 [hep-th]]. (Cited on page 21.)
Fodor, G., Forgáacs, P., Horváath, Z. and Mezei, M., “Oscillons in dilaton-scalar theories”, J. High Energy Phys., 2009(08), 106, (2009). [DOI], [arXiv:0906.4160 [hep-th]]. (Cited on page 21.)
Fodor, G., Forgáacs, P., Horváath, Z. and Mezei, M., “Radiation of scalar oscillons in 2 and 3 dimensions”, Phys. Lett. B, 674, 319–324, (2009). [DOI], [ADS], [arXiv:0903.0953 [hep-th]]. (Cited on page 21.)
Fodor, G., Forgács, P. and Mezei, M., “Boson stars and oscillatons in an inflationary universe”, Phys. Rev. D, 82, 044043, (2010). [DOI], [ADS], [arXiv:1007.0388 [gr-qc]]. (Cited on page 45.)
Fodor, G., Forgáacs, P. and Mezei, M., “Mass loss and longevity of gravitationally bound oscillating scalar lumps (oscillatons) in D-dimensions”, Phys. Rev. D, 81, 064029, (2010). [DOI], [arXiv:0912.5351 [gr-qc]]. (Cited on pages 21 and 45.)
Font, J.A., “Numerical Hydrodynamics and Magnetohydrodynamics in General Relativity”, Living Rev. Relativity, 11, lrr-2008-7, (2008). URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2008-7. (Cited on page 24.)
Font, J.A. et al., “Three-dimensional numerical general relativistic hydrodynamics. II. Long-term dynamics of single relativistic stars”, Phys. Rev. D, 65, 084024, (2002). [DOI], [ADS], [arXiv:gr-qc/0110047]. (Cited on page 28.)
Frank, R.L. and Lenzmann, E., “On ground states for the L2-critical boson star equation”, arXiv, e-print, (2009). [ADS], [arXiv:0910.2721 [math.AP]]. (Cited on page 42.)
Frank, R.L. and Lenzmann, E., “Uniqueness of ground states for the L2-critical boson star equation”, arXiv, e-print, (2009). [ADS], [arXiv:0905.3105 [math.AP]]. (Cited on page 42.)
Friedberg, R., Lee, T.D. and Pang, Y., “Mini-soliton stars”, Phys. Rev. D, 35, 3640–3657, (1987). [DOI], [ADS]. (Cited on pages 12 and 17.)
Friedberg, R., Lee, T.D. and Pang, Y., “Scalar soliton stars and black holes”, Phys. Rev. D, 35, 3658–3677, (1987). [DOI], [ADS]. (Cited on page 17.)
Friedman, J.L., Ipser, J.R. and Sorkin, R.D., “Turning-point method for axisymmetric stability of rotating relativistic stars”, Astrophys. J., 325, 722–724, (1988). [DOI], [ADS]. (Cited on pages 28 and 29.)
Gentle, S.A., Rangamani, M. and Withers, B., “A soliton menagerie in AdS”, arXiv, e-print, (2011). [ADS], [arXiv:1112.3979 [hep-th]]. (Cited on page 46.)
Gleiser, M., “Stability of boson stars”, Phys. Rev. D, 38, 2376–2385, (1988). [DOI], [ADS]. (Cited on page 28.)
Gleiser, M. and Watkins, R., “Gravitational stability of scalar matter”, Nucl. Phys. B, 319, 733–746, (1989). [DOI], [ADS]. (Cited on page 29.)
González, J.A. and Guzmán, F.S., “Interference pattern in the collision of structures in the Bose-Einstein condensate dark matter model: Comparison with fluids”, Phys. Rev. D, 83, 103513, (2011).[DOI], [ADS], [arXiv:1105.2066 [astro-ph.CO]]. (Cited on page 44.)
Gourgoulhon, E., “3+1 Formalism and Bases of Numerical Relativity”, arXiv, e-print, (2007). [arXiv:gr-qc/0703035 [GR-QC]]. (Cited on page 10.)
Grandclément, P., Fodor, G. and Forgács, P., “Numerical simulation of oscillatons: Extracting the radiating tail”, Phys. Rev. D, 84, 065037, (2011). [DOI]. (Cited on page 21.)
Guenther, R.L., A Numerical Study of the Time Dependent Schrödinger Equation Coupled with Newtonian Gravity, Ph.D. thesis, (The University of Texas, Austin, 1995). [ADS]. Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on page 18.)
Gundlach, C. and Leveque, R.J., “Universality in the run-up of shock waves to the surface of a star”, J. Fluid Mech., 676, 237–264, (2011). [DOI], [arXiv:1008.2834 [astro-ph.SR]]. (Cited on page 39.)
Gundlach, C. and Martín-García, J.M., “Critical Phenomena in Gravitational Collapse”, Living Rev. Relativity, 10, lrr-2007-5, (2007). [arXiv:0711.4620 [gr-qc]]. URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2007-5. (Cited on page 42.)
Gundlach, C. and Please, C., “Generic behaviour of nonlinear sound waves near the surface of a star: Smooth solutions”, Phys. Rev. D, 79, 067501, (2009). [DOI], [arXiv:0901.4928astro-ph.SR]]. (Cited on page 39.)
Guzmáan, F.S., “Evolving spherical boson stars on a 3D Cartesian grid”, Phys. Rev. D, 70, 044033, (2004). [DOI], [ADS], [arXiv:gr-qc/0407054]. (Cited on page 31.)
Guzmán, F.S., “Scalar fields: At the threshold of astrophysics”, J. Phys.: Conf. Ser., 91, 012003, (2007). [DOI]. (Cited on page 40.)
Guzmán, F.S., “The three dynamical fates of Boson Stars”, Rev. Mex. Fis., 55, 321–326, (2009). URL (accessed 3 February 2012): http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0035-001X2009000400011&nrm=iso. (Cited on page 32.)
Guzmán, F.S. and Rueda-Becerril, J.M., “Spherical boson stars as black hole mimickers”, Phys. Rev. D, 80, 084023, (2009). [DOI], [ADS], [arXiv:1009.1250 [astro-ph.HE]]. (Cited on page 40.)
Guzmán, F.S. and Ureña-López, L.A., “Gravitational Cooling of Self-gravitating Bose Condensates”, Astrophys. J., 645, 814–819, (2006). [DOI], [ADS], [arXiv:astro-ph/0603613]. (Cited on page 18.)
Harrison, B.K., Thorne, K.S., Wakano, M. and Wheeler, J.A., Gravitation Theory and Gravitational Collapse, (University of Chicago Press, Chicago, 1965). [ADS]. (Cited on page 29.)
Hartmann, B., Kleihaus, B., Kunz, J. and List, M., “Rotating boson stars in five dimensions”, Phys. Rev. D, 82, 084022, (2010). [DOI], [arXiv:1008.3137 [gr-qc]]. (Cited on page 45.)
Hawley, S.H. and Choptuik, M.W., “Boson stars driven to the brink of black hole formation”, Phys. Rev. D, 62, 104024, (2000). [DOI], [arXiv:gr-qc/0007039]. (Cited on page 42.)
Hawley, S.H. and Choptuik, M.W., “Numerical evidence for ‘multiscalar stars’”, Phys. Rev. D, 67, 024010, (2003). [DOI], [arXiv:gr-qc/0208078]. (Cited on page 26.)
Henriques, A.B., Liddle, A.R. and Moorhouse, R.G., “Combined boson-fermion stars”, Phys. Lett. B, 233, 99–106, (1989). [DOI], [ADS]. (Cited on page 23.)
Henriques, A.B., Liddle, A.R. and Moorhouse, R.G., “Combined boson-fermion stars: Configurations and stability”, Nucl. Phys. B, 337, 737–761, (1990). [DOI], [ADS]. (Cited on page 23.)
Heusler, M., “Stationary Black Holes: Uniqueness and Beyond”, Living Rev. Relativity, 1, lrr-1998-6, (1998). URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-1998-6. (Cited on page 20.)
Hod, S., “Quasinormal resonances of a massive scalar field in a near-extremal Kerr black hole spacetime”, Phys. Rev. D, 84, 044046, (2011). [DOI], [arXiv:1109.4080 [gr-qc]]. (Cited on page 40.)
Honda, E.P., Resonant Dynamics within the nonlinear Klein-Gordon Equation: Much ado about Oscillons, Ph.D. thesis, (The University of Texas, Austin, 2000). [ADS], [arXiv:hep-ph/0009104 [hep-ph]]. Online version (accessed 2 May 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on page 21.)
Honda, E.P., “Fractal boundary basins in spherically symmetric Φ4 theory”, Phys. Rev. D, 82, 024038, (2010). [DOI], [arXiv:1006.2421 [gr-qc]]. (Cited on page 21.)
Honda, E.P. and Choptuik, M.W., “Fine structure of oscillons in the spherically symmetric Φ4 Klein-Gordon model”, Phys. Rev. D, 65, 084037, (2002). [DOI], [arXiv:hep-ph/0110065 [hep-ph]]. (Cited on page 21.)
Jetzer, P., “Dynamical instability of bosonic stellar configurations”, Nucl. Phys. B, 316, 411–428, (1989). [DOI], [ADS]. (Cited on page 28.)
Jetzer, P., “Stability of charged boson stars”, Phys. Lett. B, 231, 433–438, (1989). [DOI], [ADS]. (Cited on page 19.)
Jetzer, P., “Stability of excited bosonic stellar configurations”, Phys. Lett. B, 222, 447–452, (1989). [DOI], [ADS]. (Cited on page 29.)
Jetzer, P., “Stability of combined boson-fermion stars”, Phys. Lett. B, 243, 36–40, (1990). [DOI], [ADS]. (Cited on page 25.)
Jetzer, P., “Boson stars”, Phys. Rep., 220, 163–227, (1992). [DOI]. (Cited on pages 7 and 29.)
Jetzer, P. and van der Bij, J.J., “Charged boson stars”, Phys. Lett. B, 227, 341–346, (1989). [DOI], [ADS]. (Cited on pages 18, 19, and 20.)
Jin, K.-J. and Suen, W.-M., “Critical Phenomena in Head-on Collisions of Neutron Stars”, Phys. Rev. Lett., 98, 131101, (2007). [DOI], [gr-qc/0603094]. (Cited on page 44.)
Kasuya, S. and Kawasaki, M., “Q-ball formation through the Affleck-Dine mechanism”, Phys. Rev. D, 61, 041301, (2000). [DOI], [ADS], [arXiv:hep-ph/9909509]. (Cited on page 17.)
Kaup, D.J., “Klein-Gordon Geon”, Phys. Rev., 172, 1331–1342, (1968). [DOI]. (Cited on pages 5 and 6.)
Kellermann, T., Rezzolla, L. and Radice, D., “Critical phenomena in neutron stars: II. Head-on collisions”, Class. Quantum Grav., 27, 235016, (2010). [DOI], [arXiv:1007.2797 [gr-qc]]. (Cited on page 44.)
Kesden, M., Gair, J. and Kamionkowski, M., “Gravitational-wave signature of an inspiral into a supermassive horizonless object”, Phys. Rev. D, 71, 044015, (2005). [DOI], [arXiv:astro-ph/0411478 [astro-ph]]. (Cited on page 40.)
Kichenassamy, S., “Soliton stars in the breather limit”, Class. Quantum Grav., 25, 245004, (2008). [DOI], [ADS]. (Cited on page 21.)
Kiessling, M.K.-H., “Monotonicity of Quantum Ground State Energies: Bosonic Atoms and Stars”, J. Stat. Phys., 137, 1063–1078, (2009). [DOI], [ADS], [arXiv:1001.4280 [math-ph]]. (Cited on page 18.)
Kleihaus, B., Kunz, J., Lämmerzahl, C. and List, M., “Charged boson stars and black holes”, Phys. Lett. B, 675, 102–109, (2009). [DOI], [ADS], [arXiv:0902.4799 [gr-qc]]. (Cited on page 19.)
Kleihaus, B., Kunz, J., Lämmerzahl, C. and List, M., “Boson shells harboring charged black holes”, Phys. Rev. D, 82, 104050, (2010). [DOI], [ADS], [arXiv:1007.1630 [gr-qc]]. (Cited on page 19.)
Kleihaus, B., Kunz, J. and List, M., “Rotating boson stars and Q-balls”, Phys. Rev. D, 72, 064002, (2005). [DOI], [ADS], [arXiv:gr-qc/0505143]. (Cited on page 17.)
Kleihaus, B., Kunz, J., List, M. and Schaffer, I., “Rotating boson stars and Q-balls. II. Negative parity and ergoregions”, Phys. Rev. D, 77, 064025, (2008). [DOI], [ADS], [arXiv:0712.3742 [gr-qc]]. (Cited on page 17.)
Kleihaus, B., Kunz, J. and Schneider, S., “Stable Phases of Boson Stars”, arXiv, e-print, (2011). [arXiv:1109.5858 [gr-qc]]. (Cited on pages 17, 23, 29, and 32.)
Kobayashi, Y., Kasai, M. and Futamase, T., “Does a boson star rotate?”, Phys. Rev. D, 50, 7721–7724, (1994). [DOI]. (Cited on page 25.)
Kouvaris, C. and Tinyakov, P.G., “Can neutron stars constrain dark matter?”, Phys. Rev. D, 82, 063531, (2010). [DOI]. (Cited on page 39.)
Kunz, J., Navarro-Lerida, F. and Viebahn, J., “Charged rotating black holes in odd dimensions”, Phys. Lett. B, 639, 362–367, (2006). [DOI], [arXiv:hep-th/0605075 [hep-th]]. (Cited on page 45.)
Kusenko, A. and Steinhardt, P.J., “Q-Ball Candidates for Self-Interacting Dark Matter”, Phys. Rev. Lett., 87, 141301, (2001). [DOI], [ADS], [arXiv:astro-ph/0106008]. (Cited on page 17.)
Kusmartsev, F.V., Mielke, E.W. and Schunck, F.E., “Gravitational Stability of Boson Stars”, Phys. Rev. D, 43, 3895–3901, (1991). [DOI], [arXiv:0810.0696 [astro-ph]]. (Cited on page 29.)
Lai, C.W., A Numerical Study of Boson Stars, Ph.D. thesis, (The University of British Columbia, Vancouver, 2004). [ADS], [arXiv:gr-qc/0410040]. Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on pages 8, 11, 14, 23, 24, 35, 43, and 44.)
Lai, C.W. and Choptuik, M.W., “Final fate of subcritical evolutions of boson stars”, arXiv, e-print, (2007). [arXiv:0709.0324 [gr-qc]]. (Cited on pages 32 and 43.)
Landsberg, G.L., “Black Holes at Future Colliders and Beyond”, J. Phys. G: Nucl. Part. Phys., 32, R337–R365, (2006). [DOI], [arXiv:hep-ph/0607297 [hep-ph]]. (Cited on page 44.)
Lee, J.W. and Lim, S., “Minimum mass of galaxies from BEC or scalar field dark matter”, J. Cosmol. Astropart. Phys., 2010(01), 007, (2010). [DOI]. (Cited on page 41.)
Lee, J.-W., “Is dark matter a BEC or scalar field?”, J. Korean Phys. Soc., 54, (2010). [arXiv:0801.1442 [astro-ph]]. (Cited on page 41.)
Lee, J.-W., Lim, S. and Choi, D., “BEC dark matter can explain collisions of galaxy clusters”, arXiv, e-print, (2008). [arXiv:0805.3827 [hep-ph]]. (Cited on page 41.)
Lee, T.D., “Soliton stars and the critical masses of black holes”, Phys. Rev. D, 35, 3637–3639, (1987). [DOI], [ADS]. (Cited on page 17.)
Lee, T.D. and Pang, Y., “Stability of mini-boson stars”, Nucl. Phys. B, 315, 477–516, (1989). [DOI], [ADS]. (Cited on pages 28 and 29.)
Lee, T.D. and Pang, Y., “Nontopological solitons”, Phys. Rep., 221, 251–350, (1992). [DOI], [ADS]. (Cited on pages 7 and 17.)
Lenzmann, E., “Uniqueness of ground states for pseudorelativistic Hartree equations”, Analysis & PDE, 2, 1–27, (2009). [DOI]. (Cited on page 42.)
Lenzmann, E. and Lewin, M., “On singularity formation for the L2-critical Boson star equation”, Nonlinearity, 24, 3515–3540, (2011). [DOI], [ADS], [arXiv:1103.3140 [math.AP]]. (Cited on page 42.)
Liddle, A.R. and Madsen, M.S., “The Structure and Formation of Boson Stars”, Int. J. Mod. Phys. D, 1, 101–143, (1992). [DOI], [ADS]. (Cited on page 7.)
Lora-Clavijo, F.D., Cruz-Osorio, A. and Guzmán, F.S., “Evolution of a massless test scalar field on boson star space-times”, Phys. Rev. D, 82, 023005, (2010). [DOI], [ADS], [arXiv:1007.1162 [gr-qc]]. (Cited on page 40.)
Lue, A. and Weinberg, E.J., “Gravitational properties of monopole spacetimes near the black hole threshold”, Phys. Rev. D, 61, 124003, (2000). [DOI], [arXiv:hep-th/0001140 [hep-th]]. (Cited on page 19.)
Lynn, B.W., “Q-stars”, Nucl. Phys., 321, 465–480, (1989). [DOI]. (Cited on page 17.)
Maldacena, J.M., “The Large-N Limit of Superconformal Field Theories and Supergravity”, Adv. Theor. Math. Phys., 2, 231–252, (1998). [DOI], [arXiv:hep-th/9711200 [hep-th]]. (Cited on page 45.)
“Maple: Math and Engineering Software by Maplesoft”, institutional homepage, Maplesoft. URL (accessed 2 May 2012): http://www.maplesoft.com. (Cited on page 19.)
Mazur, P.O. and Mottola, E., “Gravitational condensate stars: An alternative to black holes”, arXiv, e-print, (2001). [arXiv:gr-qc/0109035]. (Cited on page 40.)
McGreevy, J., “Holographic Duality with a View Toward Many-Body Physics”, Adv. High Energy Phys., 2010, 723105, (2010). [DOI], [arXiv:0909.0518 [hep-th]]. (Cited on page 45.)
Michelangeli, A. and Schlein, B., “Dynamical Collapse of Boson Stars”, Commun. Math. Phys., 311, 645–687, (2012). [DOI], [ADS], [arXiv:1005.3135 [math-ph]]. (Cited on page 18.)
Mielke, E.W. and Scherzer, R., “Geon-type solutions of the nonlinear Heisenberg-Klein-Gordon equation”, Phys. Rev. D, 24, 2111–2126, (1981). [DOI]. (Cited on page 15.)
Mielke, E.W. and Schunck, F.E., “Boson Stars: Early History and Recent Prospects”, in Piran, T. and Ruffini, R., eds., The Eighth Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, Proceedings of the meeting held at the Hebrew University of Jerusalem, 22–27 June 1997, pp. 1607–1626, (World Scientific, Singapore, 1999). [arXiv:gr-qc/9801063]. (Cited on page 7.)
Mielke, E.W. and Schunck, F.E., “Boson and Axion Stars”, in Gurzadyan, V.G., Jantzen, R.T. and Ruffini, R., eds., The Ninth Marcel Grossmann Meeting: On recent developments in theoretical and experimental general relativity, gravitation, and relativistic field theories, Proceedings of the MGIX MM meeting held at the University of Rome ‘La Sapienza’, 2–8 July 2000, pp. 581–591, (World Scientific, Singapore, 2002). (Cited on page 7.)
Milgrom, M., “A modification of the Newtonian dynamics: Implications for galaxies”, Astrophys. J., 270, 371–383, (1983). [DOI], [ADS]. (Cited on page 27.)
Milgrom, M., “MOND — Particularly as Modified Inertia”, Acta Phys. Pol. B, 42, 2175–2184, (2011). [DOI], [arXiv:1111.1611 [astro-ph.CO]]. (Cited on page 27.)
Millward, R.S. and Hirschmann, E.W., “Critical behavior of gravitating sphalerons”, Phys. Rev. D, 68, 024017, (2003). [DOI], [arXiv:gr-qc/0212015]. (Cited on page 44.)
Mundim, B.C., A Numerical Study of Boson Star Binaries, Ph.D. thesis, (The University of British Columbia, Vancouver, 2010). [ADS], [arXiv:1003.0239 [gr-qc]]. Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on pages 32, 38, and 44.)
Murariu, G., Dariescu, C. and Dariescu, M.-A., “MAPLE Routines for Bosons on Curved Manifolds”, Rom. J. Phys., 53, 99–108, (2008). (Cited on page 19.)
Murariu, G. and Puscasu, G., “Solutions for Maxwell-equations’ system in a static conformal spacetime”, Rom. J. Phys., 55, 47–52, (2010). (Cited on page 19.)
Myers, R.C. and Perry, M.J., “Black Holes in Higher Dimensional Space-Times”, Ann. Phys. (N.Y.), 172, 304, (1986). [DOI]. (Cited on page 45.)
Núñez, D., Degollado, J.C. and Moreno, C., “Gravitational waves from scalar field accretion”, Phys. Rev. D, 84, 024043, (2011). [DOI], [ADS], [arXiv:1107.4316 [gr-qc]]. (Cited on page 39.)
Page, D.N., “Classical and quantum decay of oscillations: Oscillating self-gravitating real scalar field solitons”, Phys. Rev. D, 70, 023002, (2004). [DOI], [ADS], [arXiv:gr-qc/0310006]. (Cited on page 21.)
Palenzuela, C., Lehner, L. and Liebling, S.L., “Orbital dynamics of binary boson star systems”, Phys. Rev. D, 77, 044036, (2008). [DOI], [arXiv:0706.2435 [gr-qc]]. (Cited on pages 32, 37, and 39.)
Palenzuela, C., Olabarrieta, I., Lehner, L. and Liebling, S.L., “Head-on collisions of boson stars”, Phys. Rev. D, 75, 064005, (2007). [DOI], [arXiv:gr-qc/0612067]. (Cited on pages 36 and 39.)
Pani, P., Berti, E., Cardoso, V., Chen, Y. and Norte, R., “Gravitational wave signatures of the absence of an event horizon: Nonradial oscillations of a thin-shell gravastar”, Phys. Rev. D, 80, 124047, (2009). [DOI], [ADS], [arXiv:0909.0287 [gr-qc]]. (Cited on page 41.)
Pani, P., Berti, E., Cardoso, V. and Read, J., “Compact stars in alternative theories of gravity. Einstein-Dilaton-Gauss-Bonnet gravity”, arXiv, e-print, (2011). [arXiv:1109.0928 [gr-qc]]. (Cited on page 26.)
Park, S.C., “Black holes and the LHC: A review”, arXiv, e-print, (2012). [arXiv:1203.4683 [hep-ph]]. (Cited on page 44.)
Pena, I. and Sudarsky, D., “Do collapsed boson stars result in new types of black holes?”, Class. Quantum Grav., 14, 3131–3134, (1997). [DOI]. (Cited on page 41.)
Petryk, R.J.W., Maxwell-Klein-Gordon Fields in Black Hole Spacetimes, Ph.D. thesis, (The University of British Columbia, Vancouver, 2005). [ADS]. Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on page 18.)
Pisano, F. and Tomazelli, J.L., “Stars of WIMPs”, Mod. Phys. Lett. A, 11, 647–651, (1996). [DOI], [ADS], [arXiv:gr-qc/9509022]. (Cited on page 23.)
Polchinski, J., “Introduction to Gauge/Gravity Duality”, arXiv, e-print, (2010). [arXiv:1010.6134 [hep-th]]. (Cited on page 45.)
Power, E.A. and Wheeler, J.A., “Thermal Geons”, Rev. Mod. Phys., 29, 480–495, (1957). [DOI]. (Cited on page 5.)
Psaltis, D., “Probes and Tests of Strong-Field Gravity with Observations in the Electromagnetic Spectrum”, Living Rev. Relativity, 11, lrr-2008-9, (2008). [arXiv:0806.1531 [astro-ph]]. URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2008-9. (Cited on page 40.)
Reich, E.S., “Detectors home in on Higgs boson”, Nature, 480, 301, (2011). [DOI]. (Cited on page 6.)
Rindler-Daller, T. and Shapiro, P.R., “Angular Momentum and Vortex Formation in Bose-Einstein-Condensed Cold Dark Matter Haloes”, arXiv, e-print, (2011). [arXiv:1106.1256 [astro-ph.CO]]. (Cited on page 41.)
Rosen, G., “Existence of Particlelike Solutions to Nonlinear Field Theories”, J. Math. Phys., 7, 2066–2070, (1966). [DOI], [ADS]. (Cited on page 6.)
Rousseau, B., Axisymmetric Boson Stars in the Conformally Flat Approximation, Master’s thesis, (The University of British Columbia, Vancouver, 2003). Online version (accessed 3 February 2012): http://laplace.physics.ubc.ca/Members/matt/Doc/Theses/. (Cited on page 43.)
Ruffini, R. and Bonazzola, S., “Systems of Self-Gravitating Particles in General Relativity and the Concept of an Equation of State”, Phys. Rev., 187, 1767–1783, (1969). [DOI]. (Cited on pages 6 and 10.)
Ryder, L.H., Quantum Field Theory, (Cambridge University Press, Cambridge; New York, 1996), 2nd edition. (Cited on page 6.)
Sakai, N. and Tamaki, T., “What happens to Q-balls if Q is so large?”, arXiv, e-print, (2011). [arXiv:1112.5559 [gr-qc]]. (Cited on page 19.)
Sakamoto, K. and Shiraishi, K., “Boson stars with large selfinteraction in (2+1)-dimensions: An Exact solution”, J. High Energy Phys., 1998(07), 015, (1998). [DOI], [arXiv:gr-qc/9804067 [gr-qc]]. (Cited on page 45.)
Sakamoto, K. and Shiraishi, K., “Exact solutions for boson fermion stars in (2+1)-dimensions”, Phys. Rev. D, 58, 124017, (1998). [DOI], [arXiv:gr-qc/9806040 [gr-qc]]. (Cited on page 45.)
Schunck, F.E. and Mielke, E.W., “Rotating boson stars”, in Hehl, F.W., Puntigam, R.A. and Ruder, H., eds., Relativity and Scientific Computing: Computer Algebra, Numerics, Visualization, 152nd WE-Heraeus seminar on Relativity and Scientific Computing, Bad Honnef, Germany, September 18–22, 1995, pp. 138–151, (Springer, Berlin; New York, 1996). [ADS]. (Cited on page 21.)
Schunck, F.E. and Mielke, E.W., “General relativistic boson stars”, Class. Quantum Grav., 20, R301–R356, (2003). [DOI], [arXiv:0801.0307 [astro-ph]]. (Cited on pages 5, 7, and 27.)
Schunck, F.E. and Torres, D.F., “Boson Stars with Generic Self-Interactions”, Int. J. Mod. Phys. D, 9, 601–618, (2000). [DOI], [ADS], [arXiv:gr-qc/9911038]. (Cited on page 15.)
Seidel, E. and Suen, W.-M., “Dynamical evolution of boson stars: Perturbing the ground state”, Phys. Rev. D, 42, 384–403, (1990). [DOI], [ADS]. (Cited on pages 29, 30, and 31.)
Seidel, E. and Suen, W.-M., “Oscillating soliton stars”, Phys. Rev. Lett., 66, 1659–1662, (1991). [DOI], [ADS]. (Cited on page 20.)
Seidel, E. and Suen, W.-M., “Formation of solitonic stars through gravitational cooling”, Phys. Rev. Lett., 72, 2516–2519, (1994). [DOI], [ADS], [arXiv:gr-qc/9309015]. (Cited on pages 30, 32, and 33.)
Sharma, R., Karmakar, S. and Mukherjee, S., “Boson star and dark matter”, arXiv, e-print, (2008). [ADS], [arXiv:0812.3470 [gr-qc]]. (Cited on page 41.)
Shibata, M. and Nakamura, T., “Evolution of three-dimensional gravitational waves: Harmonic slicing case”, Phys. Rev. D, 52, 5428–5444, (1995). [DOI], [ADS]. (Cited on page 31.)
Shibata, M. and Taniguchi, K., “Coalescence of Black Hole-Neutron Star Binaries”, Living Rev. Relativity, 14, lrr-2011-6, (2011). URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2011-6. (Cited on page 39.)
Shibata, M. and Yoshino, H., “Bar-mode instability of rapidly spinning black hole in higher dimensions: Numerical simulation in general relativity”, Phys. Rev. D, 81, 104035, (2010). [DOI], [arXiv:1004.4970 [gr-qc]]. (Cited on page 45.)
Silveira, V. and de Sousa, C.M.G., “Boson star rotation: A Newtonian approximation”, Phys. Rev. D, 52, 5724–5728, (1995). [DOI], [ADS], [arXiv:astro-ph/9508034]. (Cited on pages 18 and 21.)
Stewart, I., “Catastrophe theory in physics”, Rep. Prog. Phys., 45, 185–221, (1982). [DOI]. (Cited on page 29.)
Stojkovic, D., “Nontopological solitons in brane world models”, Phys. Rev. D, 67, 045012, (2003). [DOI], [arXiv:hep-ph/0111061 [hep-ph]]. (Cited on page 45.)
Stotyn, S., Park, M., McGrath, P. and Mann, R.B., “Black Holes and Boson Stars with One Killing Field in Arbitrary Odd Dimensions”, Phys. Rev. D, 85, 044036, (2012). [DOI], [arXiv:1110.2223 [hep-th]]. (Cited on page 45.)
Straumann, N., General Relativity and Relativistic Astrophysics, (Springer, Berlin; New York, 1984). [ADS]. (Cited on page 29.)
Straumann, N., “Fermion and boson stars”, in Ehlers, J. and Schäfer, G., eds., Relativistic gravity research with emphasis on experiments and observations, 81st WE-Heraeus Seminar, Aktuelle Entwicklungen in der Erforschung der relativistischen Gravitation, Bad Honnef, Germany, 2–6 September 1991, Lecture Notes in Physics, 410, (Springer, Berlin; New York, 1992). (Cited on page 7.)
Tamaki, T. and Sakai, N., “Unified picture of Q-balls and boson stars via catastrophe theory”, Phys. Rev. D, 81, 124041, (2010). [DOI], [ADS], [arXiv:1105.1498 [gr-qc]]. (Cited on pages 17 and 29.)
Tamaki, T. and Sakai, N., “Gravitating Q-balls in the Affleck-Dine mechanism”, Phys. Rev. D, 83, 084046, (2011). [DOI], [ADS], [arXiv:1105.3810 [gr-qc]]. (Cited on page 29.)
Tamaki, T. and Sakai, N., “How does gravity save or kill Q-balls?”, Phys. Rev. D, 83, 044027, (2011). [DOI], [ADS], [arXiv:1105.2932 [gr-qc]]. (Cited on page 29.)
Tamaki, T. and Sakai, N., “What are universal features of gravitating Q-balls?”, Phys. Rev. D, 84, 044054, (2011). [DOI], [ADS], [arXiv:1108.3902 [gr-qc]]. (Cited on page 29.)
Thorne, K.S., “Nonspherical gravitational collapse — A short review”, in Klauder, J., ed., Magic Without Magic: John Archibald Wheeler. A Collection of Essays in Honor of his Sixtieth Birthday, pp. 231–258, (W.H. Freeman, San Francisco, 1972). [ADS]. (Cited on page 44.)
Torres, D.F., Capozziello, S. and Lambiase, G., “Supermassive boson star at the galactic center?”, Phys. Rev. D, 62, 104012, (2000). [DOI], [ADS], [arXiv:astro-ph/0004064]. (Cited on page 40.)
Ureña-López, L.A. and Bernal, A., “Bosonic gas as a galactic dark matter halo”, Phys. Rev. D, 82, 123535, (2010). [DOI], [ADS], [arXiv:1008.1231 [gr-qc]]. (Cited on pages 26 and 41.)
Ureña-López, L.A., Matos, T. and Becerril, R., “Inside oscillatons”, Class. Quantum Grav., 19, 6259–6277, (2002). [DOI], [ADS]. (Cited on pages 20 and 21.)
Valdez-Alvarado, S., Becerril, R. and Ureña-López, L.A., “Φ4 Oscillatons”, arXiv, e-print, (2011). [arXiv:1107.3135 [gr-qc]]. (Cited on page 21.)
Vilenkin, A. and Shellard, E.P.S., Cosmic Strings and Other Topological Defects, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge; New York, 1994). (Cited on pages 6 and 19.)
Wald, R.M., General Relativity, (University of Chicago Press, Chicago, 1984). [ADS], [Google Books]. (Cited on pages 9 and 19.)
Wheeler, J.A., “Geons”, Phys. Rev., 97, 511–536, (1955). [DOI]. (Cited on page 5.)
Will, C.M., “The Confrontation between General Relativity and Experiment”, Living Rev. Relativity, 9, lrr-2006-3, (2006). [arXiv:gr-qc/0510072]. URL (accessed 1 February 2012): http://www.livingreviews.org/lrr-2006-3. (Cited on page 26.)
Yoshida, S. and Eriguchi, Y., “Rotating boson stars in general relativity”, Phys. Rev. D, 56, 762–771, (1997). [DOI], [ADS]. (Cited on pages 21 and 23.)
Yuan, Y.-F., Narayan, R. and Rees, M.J., “Constraining Alternate Models of Black Holes: Type I X-Ray Bursts on Accreting Fermion-Fermion and Boson-Fermion Stars”, Astrophys. J., 606, 1112–1124, (2004). [DOI], [ADS], [arXiv:astro-ph/0401549]. (Cited on page 40.)
Acknowledgments
It is our pleasure to thank Juan Barranco, Francisco Guzman, and Luis Lehner for their helpful comments on the manuscript. We especially appreciate the careful and critical reading by Bruno Mundim. We also thank Gyula Fodor and Péter Forgacs for their kind assistance with the section on oscillatons and oscillons. This research was supported by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation. This work was also supported by NSF grants PHY-0969827 and PHY-0803624 to Long Island University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liebling, S.L., Palenzuela, C. Dynamical Boson Stars. Living Rev. Relativ. 15, 6 (2012). https://doi.org/10.12942/lrr-2012-6
Accepted:
Published:
DOI: https://doi.org/10.12942/lrr-2012-6
Keywords
Article history
Latest
Dynamical boson stars- Published:
- 24 February 2023
- Received:
- 17 October 2022
- Accepted:
- 03 January 2023
DOI: https://doi.org/10.1007/s41114-023-00043-4
- Dynamical boson stars
- Published:
- 13 November 2017
- Received:
- 12 June 2017
- Accepted:
- 13 September 2017
DOI: https://doi.org/10.1007/s41114-017-0007-y
Original
Dynamical Boson Stars- Published:
- 08 May 2012
- Accepted:
- 29 March 2012
DOI: https://doi.org/10.12942/lrr-2012-6