Dynamo Models of the Solar Cycle

Abstract

This paper reviews recent advances and current debates in modeling the solar cycle as a hydromagnetic dynamo process. Emphasis is placed on (relatively) simple dynamo models that are nonetheless detailed enough to be comparable to solar cycle observations. After a brief overview of the dynamo problem and of key observational constraints, we begin by reviewing the various magnetic field regeneration mechanisms that have been proposed in the solar context. We move on to a presentation and critical discussion of extant solar cycle models based on these mechanisms. We then turn to the origin of fluctuations in these models, including amplitude and parity modulation, chaotic behavior, and intermittency. The paper concludes with a discussion of our current state of ignorance regarding various key questions, the most pressing perhaps being the identification of the physical mechanism(s) responsible for the generation of the Sun’s poloidal magnetic field component.

1 Introduction

1.1 Scope of review

The cyclic regeneration of the Sun’s large-scale magnetic field is at the root of all phenomena collectively known as “solar activity”. A near-consensus now exists to the effect that this magnetic cycle is to be ascribed to the inductive action of fluid motions pervading the solar interior. However, at this writing nothing resembling consensus exists regarding the detailed nature and relative importance of various possible inductive flow contributions.

My assigned task, to review “dynamo models of the solar cycle”, is daunting. For my own survival — and that of the reader — I will interpret my task as narrowly as I can get away with. This review will not discuss in any detail solar magnetic field observations, the physics of magnetic flux tubes and ropes, the generation of small-scale magnetic field in the Sun’s near-surface layers, hydromagnetic oscillator models of the solar cycle, or magnetic field generation in stars other than the Sun. Most of these topics are all worthy of full-length reviews, and do have a lot to bear on “dynamo models of the solar cycle”, but a line needs to be drawn somewhere. I also chose to exclude from consideration the voluminous literature dealing with prediction of sunspot cycle amplitudes, including the related literature focusing exclusively on the mathematical modelling of the sunspot number time series, in manner largely or even sometimes entirely decoupled from the underlying physical mechanisms of magnetic field generation.

This review thus focuses on the cyclic regeneration of the large-scale solar magnetic field through the inductive action of fluid flows, as described by various approximations and simplifications of the partial differential equations of magnetohydrodynamics. Most current dynamo models of the solar cycle rely heavily on numerical solutions of these equations, and this computational emphasis is reflected throughout the following pages. Many of the mathematical and physical intricacies associated with the generation of magnetic fields in electrically conducting astrophysical fluids are well covered in a few recent reviews (see Hoyng, 2003; Ossendrijver, 2003), and so will not be addressed in detail in what follows. The focus is on models of the solar cycle, i.e., constructs seeking primarily to describe the observed spatio-temporal variations of the Sun’s large-scale magnetic field.

1.2 What is a “model”?

The review’s very title demands an explanation of what is to be understood by “model”. A model is a theoretical construct used as thinking aid in the study of some physical system too complex to be understood by direct inferences from observed data. A model is usually designed with some specific scientific questions in mind, and researchers asking different questions about a given physical system will come up in all legitimacy with distinct model designs. A well-designed model should be as complex as it needs to be to answer the questions having motivated its inception, but no more than that. Throwing everything into a model — usually in the name of “physical realism” — is likely to produce results as complicated as the data coming from the original physical system under study. Such model results are doubly damned, as they are usually as opaque as the original physical data, and, in addition, are not even real-world data¹!

The solar dynamo models discussed in this review all rely on severe simplifications of the set of equations known to govern the dynamics of the Sun’s turbulent, magnetized fluid interior. Yet most of them are bona fide models, as defined above. Since direct numerical simulations of the solar dynamo in the appropriate parameter regime are not forthcoming, the simplified models discussed in this review are likely to remain our primary interpretative tool for solar and stellar cycles in years to come.

1.3 A brief historical survey

While regular observations of sunspots go back to the early seventeenth century, and discovery of the sunspot cycle to 1843, it is the landmark work of George Ellery Hale and collaborators that, in the opening decades of the twentieth century, demonstrated the magnetic nature of sunspots and of the solar activity cycle. In particular, Hale’s celebrated polarity laws established the existence of a well-organized toroidal magnetic flux system, residing somewhere in the solar interior, as the source of sunspots. In 1919, Larmor suggested the inductive action of fluid motions as one of a few possible explanations for the origin of this magnetic field, thus opening the path to contemporary solar cycle modelling. Larmor’s suggestion fitted nicely with Hale’s polarity laws, in that the inferred equatorial antisymmetry of the solar internal toroidal fields is precisely what one would expect from the shearing of a large-scale poloidal magnetic field by an axisymmetric and equatorially symmetric differential rotation pervading the solar interior. However, two decades later T.S. Cowling placed a major hurdle in Larmor’s path — so to speak — by demonstrating that even the most general purely axisymmetric flows could not, in themselves, sustain an axisymmetric magnetic field against Ohmic dissipation. This result became known as Cowling’s antidynamo theorem.

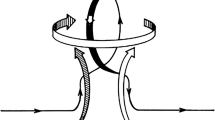
A way out of this quandary was only discovered in the mid-1950’s, when E.N. Parker pointed out that the Coriolis force could impart a systematic cyclonic twist to rising turbulent fluid elements in the solar convection, and in doing so provide the break of axisymmetry needed to circumvent Cowling’s theorem (see Figure 1). This groundbreaking idea was put on firm quantitative footing by the subsequent development of mean-field electrodynamics, which rapidly became the theory of choice for solar dynamo modelling. By the late 1970’s, concensus had almost emerged as to the fundamental nature of the solar dynamo, and the α-effect of mean-field electrodynamics was at the heart of it.

Figure 1:

Parker’s view of cyclonic turbulence twisting a toroidal magnetic field (here ribbons pointing in direction η) into meridional planes [ξ, ζ] (reproduced from Figure 1 of Parker, 1955).

Serious trouble soon appeared on the horizon, however, and from no less than four distinct directions. First, it was realized that because of buoyancy effects, magnetic fields strong enough to produce sunspots could not be stored in the solar convection zone for sufficient lengths of time to ensure adequate amplification. Second, numerical simulations of turbulent thermally-driven convection in a thick rotating spherical shell produced magnetic field migration patterns that looked nothing like what is observed on the Sun. Third, and perhaps most decisive, the nascent field of helioseismology succeeded in providing the first determinations of the solar internal differential rotation, which turned out markedly different from those needed to produce solar-like dynamo solutions in the context of mean-field electrodynamics. Fourth, the ability of the α-effect and magnetic diffusivity to operate as assumed in mean-field electrodynamics was also called into question by theoretical calculations and numerical simulations.

It is fair to say that solar dynamo modelling has not yet recovered from this four-way punch, in that nothing remotely resembling concensus currently exists as to the mode of operation of the solar dynamo. As with all major scientific crises, this situation provided impetus not only to drastically redesign existing models based on mean-field electrodynamics, but also to explore new physical mechanisms for magnetic field generation, and resuscitate older potential mechanisms that had fallen by the wayside in the wake of the α-effect — perhaps most notably the so-called Babcock-Leighton mechanism, dating back to the early 1960’s (see Figure 2). These post-helioseismic developments, beginning in the mid to late 1980’s, are the primary focus of this review.

Figure 2:

The Babcock-Leighton mechanism of poloidal field production from the decay of bipolar active regions showing opposite polarity patterns in each solar hemisphere (reproduced from Figure 8 of Babcock, 1961).

1.4 Sunspots and the butterfly diagram

Historically, next to cyclic polarity reversal the sunspot butterfly diagram has provided the most stringent observational constraints on solar dynamo models (see Figure 3). In addition to the obvious cyclic pattern, two features of the diagram are particularly noteworthy:

• Sunspots are restricted to latitudinal bands some ≃ 30° wide, symmetric about the equator.

• Sunspots emerge closer and closer to the equator in the course of a cycle, peaking in coverage at about ±15° of latitude.

Sunspots appear when deep-seated toroidal flux ropes rise through the convective envelope and emerge at the photosphere. Assuming that they rise radially and are formed where the magnetic field is the strongest, the sunspot butterfly diagram can be interpreted as a spatio-temporal “map” of the Sun’s internal, large-scale toroidal magnetic field component. This interpretation is not unique, however, since the aforementioned assumptions are questionable. In particular, we still lack even rudimentary understanding of the process through which the diffuse, large-scale solar magnetic field produces the concentrated toroidal flux ropes that will later give rise to sunspots upon buoyant destabilisation. This remains perhaps the most severe missing link between dynamo models and solar magnetic field observations. On the other hand, the stability and rise of toroidal flux ropes is now fairly well-understood (see, e.g., Fan, 2004, and references therein). In fact, from the point of view of solar cycle modelling this represents perhaps the most significant advance of the past two decades.

Figure 3:

The sunspot “butterfly diagram”, showing the fractional coverage of sunspots as a function of solar latitude and time (courtesy of D. Hathaway).

Magnetographic mapping of the Sun’s surface magnetic field (see Figure 4) have also revealed that the Sun’s poloidal magnetic component undergoes cyclic variations, changing polarities at times of sunspot maximum. Note on Figure 4 the poleward drift of the surface fields, away from sunspot latitudes. This pattern can be given two interpretations:

• It reflects the existence of a mid-to-high-latitude dynamo “branch” that, somehow, fails to produce full-blown sunspots.

• The surface fields originates from the transport of magnetic flux released by the decay of sunspots at low latitudes.

Observational evidence currently favors the second of these possibilities (but do see Petrovay and Szakály, 1999).

Figure 4:

Synoptic magnetogram of the radial component of the solar surface magnetic field. The low-latitude component is associated with sunspots. Note the polarity reversal of the weaker, high-latitude magnetic field, occurring approximately at time of sunspot maximum (courtesy of D. Hathaway).

1.5 Organization of review

The remainder of this review is organized in five sections. In Section 2 the mathematical formulation of the solar dynamo problem is laid out in some detail, together with the various simplifications that are commonly used in modelling. Section 3 details various possible physical mechanisms of magnetic field generation. In Section 4, a selection of representative models relying on different such mechanisms are presented and critically discussed, with abundant references to the technical literature. Section 5 focuses on the origin of cycle amplitude fluctuations, again presenting some illustrative model results and reviewing recent literature on the topic. The concluding Section 6 offers a somewhat more personal (i.e., even more biased!) discussion of current challenges and trends in solar dynamo modelling.

A great many review papers have been and continue to be written on dynamo models of the solar cycle, and the solar dynamo is discussed in most recent solar physics textbooks, notably Stix (2002) and Foukal (2004). The series of review articles published in Proctor and Gilbert (1994) and Ferriz-Mas and Núñez (2003) are also essential reading for more in-depth reviews of some of the topics covered here. Among the most recent reviews, Petrovay (2000); Tobias (2002); Rüdiger and Arlt (2003); Usoskin and Mursula (2003), and Ossendrijver (2003) offer (in my opinion) particularly noteworthy alternate and/or complementary viewpoints to those expressed here.

2 Making a Solar Dynamo Model

2.1 Magnetized fluids and the MHD induction equation

In the interiors of the Sun and most stars, the collisional mean-free path of microscopic constituents is much shorter than competing plasma length scales, fluid motions are non-relativistic, and the plasma is electrically neutral and non-degenerate. Under these physical conditions, Ohm’s law holds, and so does Ampere’s law in its pre-Maxwellian form. Maxwell’s equations can then be combined into a single evolution equation for the magnetic field B, known as the magnetohydro-dynamical (MHD) induction equation (see, e.g., Davidson, 2001):

$${{\partial {\bf{B}}} \over {\partial t}} = \nabla \times ({\bf{u}} \times {\bf{B}} - \eta \nabla \times {\bf{B}}),$$

(1)

where η = c²/4πσ_e is the magnetic diffusivity (σ_e being the electrical conductivity), in general only a function of depth for spherically symmetric solar/stellar structural models. Of course, the magnetic field is still subject to the divergence-free condition ∇ · B = 0, and an evolution equation for the flow field u must also be provided. This could be, e.g., the Navier-Stokes equations, augmented by a Lorentz force term:

$$\rho {{\partial {\bf{u}}} \over {\partial t}} + \rho ({\bf{u}} \cdot \nabla){\bf{u}} + 2\rho ({\bf{\Omega }} \times {\bf{u}}) = - \nabla p + \rho {\rm{g + }}{1 \over {4\pi }}(\nabla \times {\bf{B}}) \times {\bf{B}} + \nabla \cdot \tau,$$

(2)

where τ is the viscous stress tensor, and other symbols have their usual meaning². In the most general circumstances, Equations (1) and (2) must be complemented by suitable equations expressing conservation of mass and energy, as well as an equation of state. Appropriate initial and boundary conditions for all physical quantities involved then complete the specification of the problem. The resulting set of equations defines magnetohydrodynamics, quite literally the dynamics of magnetized fluids.

2.2 The dynamo problem

The first term on right hand side of Equation (1) represents the inductive action of the flow field, and thus can act as a source term for B; the second term, on the other hand, describes the resistive dissipation of the current systems supporting the magnetic field, and is thus always a global sink for B. The relative importances of these two terms is measured by the magnetic Reynolds number Rm = uL/η, obtained by dimensional analysis of Equation (1). Here η, u, and L are “typical” numerical values for the magnetic diffusivity, flow speed, and length scale over which B varies significantly. The latter, in particular, is not easy to estimate a priori, as even laminar MHD flows have a nasty habit of generating their own magnetic length scales (usually ∝ Rm^−1/2 at high Rm). Nonetheless, on length scales comparable to the large-scale solar magnetic field, Rm is immense, and so is the usual viscous Reynolds number. This implies that energy dissipation will occur on length scales very much smaller than the solar radius.

The dynamo problem consists in finding/producing a (dynamically consistent) flow field u that has inductive properties capable of sustaining B against Ohmic dissipation. Ultimately, the amplification of B occurs by stretching of the pre-existing magnetic field. This is readily seen upon rewriting the inductive term in Equation (1) as

$$\nabla \times ({\bf{u}} \times {\bf{B}}) = ({\bf{B}} \cdot \nabla){\bf{u}} - ({\bf{u}} \cdot \nabla){\bf{B}} - {\bf{B}}(\nabla \cdot {\bf{u}}).$$

(3)

In itself, the first term on the right hand side of this expression can obviously lead to exponential amplification of the magnetic field, at a rate proportional to the local velocity gradient.

In the solar cycle context, the dynamo problem is reformulated towards identifying the circumstances under which the flow fields observed and/or inferred in the Sun can sustain the cyclic regeneration of the magnetic field associated with the observed solar cycle. This involves more than merely sustaining the field. A model of the solar dynamo should also reproduce

• cyclic polarity reversals with a ∼ 10 yr half-period,

• equatorward migration of the sunspot-generating deep toroidal field and its inferred strength,

• poleward migration of the diffuse surface field,

• observed phase lag between poloidal and toroidal components,

• polar field strength,

• observed antisymmetric parity,

• predominantly negative (positive) magnetic helicity in the Northern (Southern) solar hemisphere.

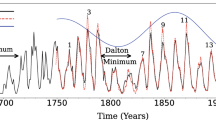
At the next level of “sophistication”, a solar dynamo model should also be able to exhibit amplitude fluctuations, and reproduce (at least qualitatively) the many empirical correlations found in the sunspot record. These include an anticorrelation between cycle duration and amplitude (Waldmeier Rule), alternance of higher-than-average and lower-than-average cycle amplitude (Gnevyshev-Ohl Rule), good phase locking, and occasional epochs of suppressed amplitude over many cycles (the so-called Grand Minima, of which the Maunder Minimum has become the archetype; more on this in Section 5 below). One should finally add to the list torsional oscillations in the convective envelope, with proper amplitude and phasing with respect to the magnetic cycle. This is a very tall order by any standard.

Because of the great disparity of time- and length scales involved, and the fact that the outer 30% in radius of the Sun are the seat of vigorous, thermally-driven turbulent convective fluid motions, the solar dynamo problem is rarely tackled as a direct numerical simulation of the full set of MHD equations (but do see Section 4.9 below). Most solar dynamo modelling work has thus relied on simplification — usually drastic — of the MHD equations, as well as assumptions on the structure of the Sun’s magnetic field and internal flows.

2.3 Kinematic models

A first drastic simplification of the MHD system of equations consists in dropping Equation (2) altogether by specifying a priori the form of the flow field u. This kinematic regime remained until relatively recently the workhorse of solar dynamo modelling. Note that with u given, the MHD induction equation becomes truly linear in B. Moreover, helioseismology has now pinned down with good accuracy two important solar large-scale flow components, namely differential rotation throughout the interior, and meridional circulation in the outer half of the solar convection zone (for a recent and comprehensive review, see Christensen-Dalsgaard, 2002). Given the low amplitude of observed torsional oscillations in the solar convective envelope, and the lack of significant cycle-related changes in the internal solar differential rotation inferred by helioseismology to this date, the kinematic approximation is perhaps not as bad a working assumption as one may have thought, at least for the differential rotation part of the mean flow u.

2.4 Axisymmetric formulation

The sunspot butterfly diagram, Hale’s polarity law, synoptic magnetograms, and the shape of the solar corona at and around solar activity minimum jointly suggest that, to a tolerably good first approximation, the large-scale solar magnetic field is axisymmetric about the Sun’s rotation axis, as well as antisymmetric about the equatorial plane. Under these circumstances it is convenient to express the large-scale field as the sum of a toroidal (i.e., longitudinal) component and a poloidal component (i.e., contained in meridional planes), the latter being expressed in terms of a toroidal vector potential. Working in spherical polar coordinates (r, θ, φ), one writes

$${\bf{B}}(r, \theta, t) = \nabla \times (A(r, \theta, t){{\bf{\hat e}}_\phi }) + B(r, \theta, t){{\bf{\hat e}}_\phi}.$$

(4)

Such a decomposition evidently satisfies the solenoidal constraint ∇ • B = 0, and substitution into the MHD induction equation produces two (coupled) evolution equations for A and B, the latter simply given by the φ-component of Equation (1), and the former, under the Coulomb gauge ∇ · A = 0, by

$${{\partial A} \over {\partial t}} + ({\bf{u}} \cdot \nabla)(A{{\bf{\hat e}}_\phi }) = \eta {\nabla ^2}(A{{\bf{\hat e}}_\phi}).$$

(5)

2.5 Boundary conditions and parity

The axisymmetric dynamo equations are to be solved in a meridional plane, i.e., R_i ≤ r ≤ R_⊙ and 0 ≤ θ ≤ π, where the inner radial extent of the domain (R_i) need not necessarily extend all the way to r = 0. It is usually assumed that the deep radiative interior can be treated as a perfect conductor, so that R_i is chosen a bit deeper than the lowest extent of the region where dynamo action is taking place; the boundary condition at this depth is then simply A = 0, ∂(rB)/∂r = 0.

It is usually assumed that the Sun/star is surrounded by a vacuum, in which no electrical currents can flow, i.e., ∇ × B = 0; for an axisymmetric B expressed via Equation (4), this requires

$$\left({{\nabla ^2} - {1 \over {{\varpi ^2}}}} \right)A = 0,\quad \quad B = 0,\quad \quad r/{R_ \odot } > 1.$$

(6)

It is therefore necessary to smoothly match solutions to Equations (1, 5) on solutions to Equations (6) at r/R_⊙ = 1. Regularity of the solutions demands that A = 0 and B = 0 on the symmetry axis (θ = 0 and θ = π in a meridional plane). This completes the specification of the boundary conditions.

Formulated in this manner, the dynamo solution will spontaneously “pick” its own parity, i.e., its symmetry with respect to the equatorial plane. An alternative approach, popular because it can lead to significant savings in computing time, is to solve only in a meridional quadrant (0 ≤ θ ≤ π/2) and impose solution parity via the boundary condition at the equatorial plane (π/2):

$${{\partial A} \over {\partial \theta}} = 0,\quad \quad B = 0\quad \quad \rightarrow \;\;{\rm{antisymmetric}},$$

(7)

$$A = 0,\quad \quad {{\partial B} \over {\partial \theta }} = 0\quad \quad \rightarrow \;\;{\rm{symmetric}}.$$

(8)

3 Mechanisms of Magnetic Field Generation

The Sun’s poloidal magnetic component, as measured on photospheric magnetograms, flips polarity near sunspot cycle maximum, which (presumably) corresponds to the epoch of peak internal toroidal field T. The poloidal component P, in turn, peaks at time of sunspot minimum. The cyclic regeneration of the Sun’s full large-scale field can thus be thought of as a temporal sequence of the form

$$P(+) \rightarrow T(-) \rightarrow P(-) \rightarrow T(+) \rightarrow P(+) \rightarrow \ldots,$$

(9)

where the (+) and (−) refer to the signs of the poloidal and toroidal components, as established observationally. A full magnetic cycle then consists of two successive sunspot cycles. The dynamo problem can thus be broken into two sub-problems: generating a toroidal field from a pre-existing poloidal component, and a poloidal field from a pre-existing toroidal component. In the solar case, the former turns out to be easy, but the latter is not.

3.1 Poloidal to toroidal

Let us begin by expressing the (steady) large-scale flow field u as the sum of an axisymmetric azimuthal component (differential rotation), and an axisymmetric “poloidal” component u_p (≡ u_r (r, θ)ê_r + u_θ(r, θ)ê_θ), i.e., a flow confined to meridional planes:

$${\bf{u}}(r,\theta) = {{\bf{u}}_{\rm{p}}}(r,\theta) + \varpi \Omega (r,\theta){{\bf{\hat e}}_\phi}$$

(10)

where ϖ = r sin θ and Ω is the angular velocity (rad s⁻¹). Substituting this expression into Equation (5) and into the φ-components of Equation (1) yields

$${{\partial A} \over {\partial t}} = \underbrace {\eta \left({{\nabla ^2} - {1 \over {{\varpi ^2}}}} \right)A}_{{\rm{resistive}}\,{\rm{decay}}} - \underbrace {{{{{\bf{u}}_{\rm{p}}}} \over \varpi } \cdot \nabla (\varpi A)}_{{\rm{advection}}},$$

(11)

$${{\partial B} \over {\partial t}} = \underbrace {\eta \left({{\nabla ^2} - {1 \over {{\varpi ^2}}}} \right)B}_{{\rm{resistive}}\,{\rm{decay}}} + \underbrace {{1 \over \varpi }{{\partial (\varpi B)} \over {\partial r}}{{\partial \eta } \over {\partial r}}}_{{\rm{diamagnetic}}\,{\rm{transport}}} - \underbrace {\varpi {{\bf{u}}_{\rm{p}}} \cdot \nabla \left({{B \over \varpi }} \right)}_{{\rm{advection}}} - \underbrace {B\nabla \cdot {{\bf{u}}_{\rm{p}}}}_{{\rm{compression}}} + \underbrace {\varpi (\nabla \times (A{{{\bf{\hat e}}}_\phi })) \cdot \nabla \Omega }_{{\rm{shearing}}}.$$

(12)

Advection means bodily transport of B by the flow; globally, this neither creates nor destroys magnetic flux. Resistive decay, on the other hand, destroys magnetic flux and therefore acts as a sink of magnetic field. Diamagnetic transport can increase B locally, but again this is neither a source nor sink of magnetic flux. The compression/dilation term is a direct consequence of toroidal flux conservation in a meridional flow moving across a density gradient. The shearing term in Equation (12), however, is a true source term, as it amounts to converting rotational kinetic energy into magnetic energy. This is the needed P → T production mechanism.

However, there is no comparable source term in Equation (11). No matter what the toroidal component does, A will inexorably decay. Going back to Equation (12), notice now that once A is gone, the shearing term vanishes, which means that B will in turn inexorably decay. This is the essence of Cowling’s theorem: An axisymmetric flow cannot sustain an axisymmetric magnetic field against resistive decay³.

3.2 Toroidal to poloidal

In view of Cowling’s theorem, we have no choice but to look for some fundamentally non-axisymmetric process to provide an additional source term in Equation (11). It turns out that under solar interior conditions, there exist various mechanisms that can act as a source of poloidal field. In what follows we introduce and briefly describe the four classes of mechanisms that appear most promising, but defer discussion of their implementation in dynamo models to Section 4, where illustrative solutions are also presented.

3.2.1 Turbulence and mean-field electrodynamics

The outer ∼ 30% of the Sun are in a state of thermally-driven turbulent convection. This turbulence is anisotropic because of the stratification imposed by gravity, and of the influence of Coriolis forces on turbulent fluid motions. Since we are primarily interested in the evolution of the large-scale magnetic field (and perhaps also the large-scale flow) on time scales longer than the turbulent time scale, mean-field electrodynamics offers a tractable alternative to full-blown 3D turbulent MHD. The idea is to express the net flow and field as the sum of mean components, 〈u〉 and 〈B〉, and small-scale fluctuating components u′, B′. This is not a linearization procedure, in that we are not assuming that |u′|/| 〈u〉 | ≪ 1 or |B′|/| 〈B〉 | ≪ 1. In the context of the axisymmetric models to be described below, the averaging (“〈 〉”) is most naturally interpreted as a longitudinal average, with the fluctuating flow and field components vanishing when so averaged, i.e., 〈u′〉 = 0 and 〈B′〉 = 0. The mean field 〈B〉 is then interpreted as the large-scale, axisymmetric magnetic field usually associated with the solar cycle. Upon this separation and averaging procedure, the MHD induction equation for the mean component becomes

$${{\partial \langle {\bf{B}} \rangle} \over {\partial t}} = \nabla \times (\langle {\bf{u}} \rangle \times \langle {\bf{B}} \rangle + \langle {{{\bf{u}}^{\prime}} \times {{\bf{B}}^{\prime}}} \rangle - \eta \nabla \times \langle {\bf{B}} \rangle).$$

(13)

which is identical to the original MHD induction Equation (1) except for the term 〈u′ × B′〉, which corresponds to a mean electromotive force ɛ induced by the fluctuating flow and field components. It appears here because, in general, the cross product u′ × B′ will not necessarily vanish upon averaging, even though u′ and B′ do so individually. Evidently, this procedure is meaningful if a separation of spatial and/or temporal scales exists between the (time-dependent) turbulent motions and associated small-scale magnetic fields on the one hand, and the (quasi-steady) large-scale axisymmetric flow and field on the other.

The reader versed in fluid dynamics will have recognized in the mean electromotive force the equivalent of Reynolds stresses appearing in mean-field versions of the Navier-Stokes equations, and will have anticipated that the next (crucial!) step is to express ɛ in terms of the mean field 〈B〉 in order to achieve closure. This is usually carried out by expressing ɛ as a truncated series expansion in 〈B〉 and its derivatives. Retaining the first two terms yields

$${\cal E} = \alpha :\langle {\bf{B}} \rangle + \beta :\nabla \times \langle {\bf{B}} \rangle.$$

(14)

where the colon indicates an inner product. The quantities α and β are in general pseudo-tensors, and specification of their components requires a turbulence model from which averages of velocity cross-correlations can be computed, which is no trivial task. We defer discussion of specific model formulations for these quantities to Section 4.2, but note the following:

• Even if 〈B〉 is axisymmetric, the α-term in Equation (14) will effectively introduce source terms in both the A and B equations, so that Cowling’s theorem can be circumvented.

• Parker’s idea of helical twisting of toroidal fieldlines by the Coriolis force corresponds to a specific functional form for α, and so finds formal quantitative expression in mean-field electrodynamics.

The production of a mean electromotive force proportional to the mean field is called the α-effect. Its existence was first demonstrated in the context of turbulent MHD, but it also arises in other contexts, as discussed immediately below. Although this is arguably a bit of a physical abuse, the term “α-effect” is used in what follows to denote any mechanism producing a mean poloidal field from a mean toroidal field, as is almost universally (and perhaps unfortunately) done in the contemporary solar dynamo literature.

3.2.2 Hydrodynamical shear instabilities

The tachocline is the rotational shear layer uncovered by helioseismology immediately beneath the Sun’s convective envelope, providing smooth matching between that latitudinal differential rotation of the envelope, and the rigidly rotating radiative core (see, e.g., Spiegel and Zahn, 1992; Brown et al., 1989; Tomczyk et al., 1995; Charbonneau et al., 1999a, and references therein). While the latitudinal shear in the tachocline has been shown to be hydrodynamically stable with respect to Rayleigh-type 2D instabilities on a spherical shell (see, e.g., Charbonneau et al., 1999b, and references therein), further analysis allowing vertical displacement in the framework of shallow-water theory suggests that the latitudinal shear can become unstable when vertical fluid displacement is allowed (Dikpati and Gilman, 2001). These authors also find that vertical fluid displacements correlate with the horizontal vorticity pattern in a manner resulting in a net kinetic helicity that can, in principle, impart a systematic twist to an ambient mean toroidal field. This can thus serve as a source for the poloidal component, and, in conjunction with rotational shearing of the poloidal field, lead to cyclic dynamo action. This is a self-excited T → P mechanism, but it is not entirely clear at this juncture if (and how) it would operate in the strong-field regime (more on this in Section 4.5 below). From the modelling point of view, it amounts to a mean-field-like α-effect confined to the uppermost radiative portion of the solar tachocline, and peaking at mid-latitudes.

3.2.3 MHD instabilities

It has now been demonstrated, perhaps even beyond reasonable doubt, that the toroidal magnetic flux ropes that upon emergence in the photosphere give rise to sunspots can only be stored below the Sun’s convective envelope, more specifically in the thin, weakly subadiabatic overshoot layer conjectured to exist immediately beneath the core-envelope interface (see, e.g., Schüssler, 1996; Schüssler and Ferriz-Mas, 2003; Fan, 2004, and references therein), Only there are growth rates for the magnetic buoyancy instability sufficiently long to allow field amplification, while being sufficiently short for flux emergence to take place on time-scales commensurate with the solar cycle (Ferriz-Mas et al., 1994). These stability studies have also revealed the existence of regions of weak instability, in the sense that the growth rates are numbered in years. The developing instability is then strongly influenced by the Coriolis force, and thus develops in the form of growing helical waves travelling along the flux rope’s axis. This amounts to twisting a toroidal field in meridional planes, as with the Parker scenario, with the important difference that what is now being twisted is a flux rope rather than an individual fieldline. Nonetheless, an azimuthal electromotive force is produced. This represents a viable T → P mechanism, but one that can only act above a certain field strength threshold; in other words, dynamos relying on this mechanism are not self-excited, since they require strong fields to operate. On the other hand, they operate without difficulties in the strong field regime.

Another related class of poloidal field regeneration mechanism is associated with the buoyant breakup of the magnetized layer (Matthews et al., 1995). Once again it is the Coriolis force that ends up imparting a net twist to the rising, arching structures that are produced in the course of the instability’s development (see Thelen, 2000a, and references therein). This results in a mean electromotive force that peaks where the magnetic field strength varies most rapidly with height. This could provide yet another form of tachocline α-effect, again subjected to a lower operating threshold.

3.2.4 The Babcock-Leighton mechanism

The larger sunspot pairs (“bipolar magnetic regions”, hereafter BMR) often emerge with a systematic tilt with respect to the E-W direction, in that the leading sunspot (with respect to the direction of solar rotation) is located at a lower latitude than the trailing sunspot, the more so the higher the latitude of the emerging BMR. This pattern, known as “Joy’s law”, is caused by the action of the Coriolis force on the secondary azimuthal flow that develops within the buoyantly rising magnetic toroidal flux rope that, upon emergence, produces a BMR (see, e.g. Fan et al., 1993; D’Silva and Choudhuri, 1993; Caligari et al., 1995). This tilt is at the heart of the Babcock-Leighton mechanism for polar field reversal, as outlined in cartoon form in Figure 2.

Mathematically, the Babcock-Leighton mechanism can be understood in the following manner; the surface distribution of radial magnetic field associated with a BMR ($B_{r}^{0}(\theta,\phi)$, say) can, as with any continuous function defined on a sphere, be decomposed into spherical harmonics:

$$B_r^0(\theta, \phi) = \sum\limits_{l = 1}^\infty {} \sum\limits_{m = - l}^{ + l} {{b_{lm}}} {y_{lm}}(\theta, \phi).$$

(15)

Now at high Rm, under the joint action of differential rotation and magnetic dissipation, all non-axisymmetric (i.e., m ≠ 0) terms will be destroyed on a timescale much faster than diffusive, a process known as axisymmetrization that is the spherical equivalent of the well-known process of magnetic flux expulsion by closed circulatory flows. Therefore, after some time the surface radial field will assume the form

$${B_r}(\theta) = \sum\limits_{l = 1}^\infty {\sqrt {{{2l + 1} \over {4\pi }}} } {b_{l0}}{P_l}(\cos \theta),$$

(16)

where the P_l;(cos θ) are the Legendre polynomials. Equation (16) now describes an axisymmetric poloidal field. Since the BMR field was oriented in the toroidal direction prior to destabilization, rise, and emergence, the net effect is to produce a poloidal field out of a toroidal field, thus offering a viable T → P mechanism. Here again the resulting dynamos are not self-excited, as the required tilt of the emerging BMR only materializes in a range of toroidal field strength going from a few 10⁴ G to about 2 × 10⁵ G.

4 A Selection of Representative Models

Each and every one of the T → P mechanisms described in Section 3.2 relies on fundamentally non-axisymmetric physical effects, yet these must be “forced” into axisymmetric dynamo equations for the mean magnetic field. There are a great many different ways of doing so, which explains the wide variety of dynamo models of the solar cycle to be found in the recent literature. The aim of this section is to provide representative examples of various classes of models, to highlight their similarities and differences, and illustrate their successes and failings. In all cases, the model equations are to be understood as describing the evolution of the mean field 〈B〉, namely the large-scale, axisymmetric component of the total solar magnetic field.

4.1 Model ingredients

All solar dynamo models have some basic “ingredients” in common, most importantly (i) a solar structural model, (ii) a differential rotation profile, and (iii) a magnetic diffusivity profile (possibly depth-dependent). Meridional circulation in the convective envelope, long considered unimportant from the dynamo point of view, has gained popularity in recent years, initially in the Babcock-Leighton context but now also in other classes of models.

Helioseismology has pinned down with great accuracy the internal solar structure, including the internal differential rotation, and the exact location of the core-envelope interface. Unless noted otherwise, all illustrative models discussed in this section were computed using the following analytic formulae for the angular velocity Ω(r, θ) and magnetic diffusivity η(r):

$${{\Omega (r,\theta)} \over {{\Omega _{\rm{E}}}}} = {\Omega _{\rm{C}}} + {{{\Omega _{\rm{S}}}(\theta) - {\Omega _{\rm{C}}}} \over 2}\left[ {1 + {\rm{erf}}\left({{{r - {r_{\rm{c}}}} \over w}} \right)} \right],$$

(17)

with

$${\Omega _{\rm{S}}}(\theta) = 1 - {a_2}{\cos ^2}\theta - {a_4}{\cos ^4}\theta,$$

(18)

and

$${{\eta (r)} \over {{\eta _{\rm{T}}}}} = \Delta \eta + {{1 - \Delta \eta } \over 2}\left[ {1 + {\rm{erf}}\left({{{r - {r_{\rm{c}}}} \over w}} \right)} \right].$$

(19)

With appropriately chosen parameter values, Equation (17) describes a solar-like differential rotation profile, namely a purely latitudinal differential rotation in the convective envelope, with equatorial acceleration and smoothly matching a core rotating rigidly at the angular speed of the surface mid-latitudes⁴. This rotational transition takes place across a spherical shear layer of half-thickness w coinciding with the core-envelope interface at r_c/R_⊙ = 0.7 (see Figure 5, with parameter values listed in caption). As per Equation (19), a similar transition takes place with the net diffusivity, falling from some large, “turbulent” value η_T in the envelope to a much smaller diffusivity η_C in the convection-free radiative core, the diffusivity contrast being given by Δη = η_C/η_t. Given helioseismic constraints, these represent minimalistic yet reasonably realistic choices.

Figure 5:

Isocontours of angular velocity generated by Equation (17), with parameter values w/R = 0.05, Ω_C = 0.8752, a₂ = 0.1264, a₄ = 0.1591 (Panel A). The radial shear changes sign at colatitude θ = 55^°. Panel B shows the corresponding angular velocity gradients, together with the total magnetic diffusivity profile defined by Equation (19) (dash-dotted line). The core-envelope interface is located at r/R_⊙ = 0.7 (dotted lines).

It should be noted already that such a solar-like differential rotation profile is quite complex from the point of view of dynamo modelling, in that it is characterized by three partially overlapping shear regions: a strong positive radial shear in the equatorial regions of the tachocline, an even stronger negative radial shear in its the polar regions, and a significant latitudinal shear throughout the convective envelope and extending partway into the tachocline. As shown on Panel B of Figure 5, for a tachocline of half-thickness w/R_⊙ = 0.05, the mid-latitude latitudinal shear at r/R_⊙ = 0.7 is comparable in magnitude to the equatorial radial shear; its potential contribution to dynamo action should not be casually dismissed.

Ultimately, the magnetic diffusivities and differential rotation in the convective envelope owe their existence to the turbulence therein, more specifically to the associated Reynolds stresses. While it has been customary in solar dynamo modelling to simply assume plausible functional forms for these quantities (such as Equations (17, 18, 19) above), one recent trend has been to calculate these quantities in an internally consistent manner using an actual model for the turbulence itself (see, e.g., Kitchatinov and Rüdiger, 1993). While this approach introduces additional — and often important — uncertainties at the level of the turbulence model, it represents in principle a tractable avenue out of the kinematic regime.

4.2 αΩ mean-field models

4.2.1 Calculating the α-effect and turbulent diffusivity

Mean-field electrodynamics is a subject well worth its own full-length review, so the foregoing discussion will be limited to the bare essentials. Detailed discussion of the topic can be found in Krause and Rädler (1980); Moffatt (1978), and in the recent review article by Hoyng (2003).

The task at hand is to calculate the components of the α and β tensor in terms of the statistical properties of the underlying turbulence. A particularly simple case is that of homogeneous, weakly isotropic turbulence, which reduces the α and β tensor to simple scalars, so that the mean electromotive force becomes

$${\cal E} = \alpha \langle {\bf{B}} \rangle - {\eta _{\rm{T}}}\nabla \times \langle {\bf{B}} \rangle.$$

(20)

This is the form commonly used in solar dynamo modelling, even though turbulence in the solar interior is most likely inhomogeneous and anisotropic. Moreover, hiding in the above expressions is the assumption that the small-scale magnetic Reynolds number υℓ/η is much smaller than unity, where υ ∼ 10³ cm s⁻¹ and ℓ ∼ 10⁹ cm are characteristic velocities and length scales for the dominant turbulent eddies, as estimated, e.g., from mixing length theory. With η ∼ 10⁴ cm² s⁻¹, one finds υℓ/η ∼ 10⁸, so that on that basis alone Equation (20) should be dubious already. In the kinematic regime, α and β are independent of the magnetic field fluctuations, and end up simply proportional to the averaged kinetic helicity and square fluctuation amplitude:

$$\alpha \sim - {{{\tau _{\rm{c}}}} \over 3}\langle {{{\bf{u}}^{\prime}} \cdot \nabla \times {{\bf{u}}^{\prime}}} \rangle,$$

(21)

$${\eta _{\rm{T}}}\sim{{{\tau _{\rm{c}}}} \over 3}\langle {{{\bf{u}}^{\prime}} \cdot {{\bf{u}}^{\prime}}} \rangle,$$

(22)

where τ_c is the correlation time of the turbulent motions. Order-of-magnitude estimates of the scalar coefficients yield α ∼ Ωℓ and η_T ∼ υℓ, where Ω is the solar angular velocity. At the base of the solar convection zone, one then finds α ∼ 10³ cm s⁻¹ and η_T ∼ 10¹² cm² s⁻¹, these being understood as very rough estimates. Because the kinetic helicity may well change sign along the longitudinal (averaging) direction, thus leading to cancellation, the resulting value of α may be much smaller than its r.m.s. deviation about the longitudinal mean. In contrast the quantity being averaged on the right hand side of Equation (22) is positive definite, so one would expect a more “stable” mean value (see Hoyng, 1993; Ossendrijver et al., 2001, for further discussion). At any rate, difficulties in computing α and η_T from first principle (whether as scalars or tensors) have led to these quantities often being treated as adjustable parameters of mean-field dynamo models, to be adjusted (within reasonable bounds) to yield the best possible fit to observed solar cycle characteristics, most importantly the cycle period. One finds in the literature numerical values in the approximate ranges 10–10³ cm s−¹ for α and 10¹⁰–10¹³ cm² s⁻¹ for η_T.

The cyclonic character of the α-effect also indicates that it is equatorially antisymmetric and positive in the Northern solar hemisphere, except perhaps at the base of the convective envelope, where the rapid variation of the turbulent velocity with depth can lead to sign change. These expectations have been confirmed in a general sense by theory and numerical simulations (see, e.g., Rüdiger and Kitchatinov, 1993; Brandenburg et al., 1990; Ossendrijver et al., 2001).

Leaving the kinematic regime, it is expected that both α and β should depend on the strength of the magnetic field, since magnetic tension will resist deformation by the small-scale turbulent fluid motions. The groundbreaking numerical MHD simulations of Pouquet et al. (1976) suggested that Equation (21) should be replaced by something like

$$\alpha \sim - {{{\tau _{\rm{c}}}} \over 3}[\langle {{{\bf{u}}^{\prime}} \cdot \nabla \times {{\bf{u}}^{\prime}}} \rangle - \langle {{{\bf{a}}^{\prime}} \cdot \nabla \times {{\bf{a}}^{\prime}}} \rangle],$$

(23)

where ${\bf a}^{\prime}={\bf b}^{\prime}\sqrt{4\pi\rho}$ is the Alfvén speed based on the small-scale magnetic component (see also Durney et al., 1993; Blackman and Brandenburg, 2002). This is rarely used in solar cycle modelling, since the whole point of the mean-field approach is to avoid dealing explicitly with the small-scale, fluctuating components. On the other hand, something is bound to happen when the growing dynamo-generated mean magnetic field reaches a magnitude such that its energy per unit volume is comparable to the kinetic energy of the underlying turbulent fluid motions. Denoting this equipartition field strength by B_eq, one often introduces an ad hoc nonlinear dependency of α (and sometimes η_T as well) directly on the mean-field 〈B〉 by writing:

$$\alpha \rightarrow \alpha (\langle {\bf{B}} \rangle) = {{{\alpha _0}} \over {1 + {{(\langle {\bf{B}} \rangle/{B_{{\rm{eq}}}})}^2}}}.$$

(24)

This expression “does the right thing”, in that α → 0 as 〈B〉 starts to exceed B_eq. It remains an extreme oversimplification of the complex interaction between flow and field that characterizes MHD turbulence, but its wide usage in solar dynamo modeling makes it a nonlinearity of choice for the illustrative purpose of this section.

4.2.2 The αΩ dynamo equations

Adding this contribution to the MHD induction equation leads to the following form for the axisymmetric mean-field dynamo equations:

$${{\partial \langle A \rangle} \over {\partial t}} = \underbrace {(\eta + {\eta _{\rm{T}}})\left({{\nabla ^2} - {1 \over {{\varpi ^2}}}} \right)\langle A \rangle }_{{\rm{turbulent}}\,{\rm{diffusion}}} - {{{{\bf{u}}_{\rm{p}}}} \over \varpi } \cdot \nabla (\varpi \langle A \rangle) + \underbrace {\alpha \langle B \rangle }_{{\rm{MFE}}\,{\rm{source}}},$$

(25)

$$\matrix{{{{\partial \langle B \rangle } \over {\partial t}} = \underbrace {(\eta + {\eta _{\rm{T}}})\left({{\nabla ^2} - {1 \over {{\varpi ^2}}}} \right)\langle B \rangle }_{{\rm{turbulent}}\;{\rm{diffusion}}} + \underbrace {{1 \over \varpi }{{\partial \varpi \langle B \rangle } \over {\partial r}}{{\partial (\eta + {\eta _{\rm{T}}})} \over {\partial r}}}_{{\rm{turbulent}}\;{\rm{diamagnetic}}\;{\rm{transport}}} - \varpi {{\bf{u}}_{\rm{p}}} \cdot \nabla \left({{{\langle B \rangle } \over \varpi }} \right) - \langle B \rangle \nabla \cdot {{\bf{u}}_{\rm{p}}}} \hfill \cr {\quad \quad \quad + \underbrace {\varpi (\nabla \times (\langle A \rangle {{{\bf{\hat e}}}_\phi })) \cdot \nabla \Omega }_{{\rm{shearing}}} + \underbrace {\nabla \times [\alpha \nabla \times (\langle A \rangle {\bf{\hat e}}\;\phi)]}_{{\rm{MFE}}\;{\rm{source}}},} \hfill \cr}$$

(26)

where, in general, η_T ≫ η There are source terms on both right hand sides, so that dynamo action is now possible in principle. The relative importance of the α-effect and shearing terms in Equation (26) is measured by the ratio of the two dimensionless dynamo numbers

$${C_\alpha } = {{{\alpha _0}{R_ \odot }} \over {{\eta _0}}},\quad \quad {C_\Omega } = {{{{(\Delta \Omega)}_0}R_ \odot ^2} \over {{\eta _0}}},$$

(27)

where, in the spirit of dimensional analysis, α₀, η₀, and (ΔΩ)₀ are “typical” values for the α-effect, turbulent diffusivity, and angular velocity contrast. These quantities arise naturally in the non-dimensional formulation of the mean-field dynamo equations, when time is expressed in units of the magnetic diffusion time t based on the envelope (turbulent) diffusivity:

$$\tau = {{R_ \odot ^2} \over {{\eta _{\rm{T}}}}}.$$

(28)

In the solar case, it is usually estimated that C_α ≪ C_Ω, so that the α-term is neglected in Equation (26); this results in the class of dynamo models known as αΩ dynamo, which will be the only ones discussed here⁵.

4.2.3 Eigenvalue problems and initial value problems

With the large-scale flows, turbulent diffusivity and α-effect considered given, Equations (25, 26) become truly linear in A and B. It becomes possible to seek eigensolutions in the form

$$\langle A \rangle (r, \theta, t) = a(r,\theta)\exp (st),\quad \quad \langle B \rangle (r, \theta, t) = b(r,\theta)\exp (st).$$

(29)

Substitution of these expressions into Equations (25, 26) yields an eigenvalue problem for s and associated eigenfunction {a, b}. The real part σ ≡ Re s is then a growth rate, and the imaginary part w ≡ Im s an oscillation frequency. One typically finds that σ < 0 until the product C_α × C_Ω exceeds a certain critical value D_crit beyond which σ > 0, corresponding to a growing solutions. Such solutions are said to be supercritical, while the solution with α = 0 is critical.

Clearly exponential growth of the dynamo-generated magnetic field must cease at some point, once the field starts to backreact on the flow through the Lorentz force. This is the general idea embodied in α-quenching. If α-quenching — or some other nonlinearity — is included, then the dynamo equations are usually solved as an initial-value problem, with some arbitrary low-amplitude seed field used as initial condition. Equations (25, 26) are then integrated forward in time using some appropriate time-stepping scheme. A useful quantity to monitor in order to ascertain saturation is the magnetic energy within the computational domain:

$${{\cal E}_B} = {1 \over {8\pi }}\int_V {{{\langle {\bf{B}} \rangle }^2}} dV.$$

(30)

4.2.4 Dynamo waves

One of the most remarkable property of the (linear) α_Ω dynamo equations is that they support travelling wave solutions. This was first demonstrated in Cartesian geometry by Parker (1955), who proposed that a latitudinally-travelling “dynamo wave” was at the origin of the observed equatorward drift of sunspot emergences in the course of the cycle. This finding was subsequently shown to hold in spherical geometry, as well as for non-linear models (Yoshimura, 1975; Stix, 1976). Dynamo waves⁶ travel in a direction s given by

$${\bf{s}} = \alpha \nabla \Omega \times {{\bf{\hat e}}_\phi},$$

(31)

a result now known as the “Parker-Yoshimura sign rule”. Recalling the rather complex form of the helioseismically inferred solar internal differential rotation (cf. Figure 5), even an α-effect of uniform sign in each hemisphere can produce complex migratory patterns, as will be apparent in the illustrative αΩ dynamo solutions to be discussed shortly. Note already at this juncture that if the seat of the dynamo is to be identified with the low-latitude portion of the tachocline, and if the latter is thin enough for the (positive) radial shear therein to dominate over the latitudinal shear, then equatorward migration of dynamo waves will require a negative α-effect in the low latitudes of the Northern solar hemisphere.

4.2.5 Representative results

We first consider αΩ models without meridional circulation (u_p = 0 in Equations (25, 26)), with the α-term omitted in Equation (26), and using the diffusivity profile and angular velocity profile of Figure 5. We will investigate the behavior of αΩ models with the α-effect operating throughout the bulk of the convective envelope (red line in Figure 6), as well as with an α-effect concentrated just above the core-envelope interface (green line in Figure 6). We also consider two latitudinal dependencies, namely α ∝ cos θ, which is the “minimal” possible latitudinal dependency compatible with the required equatorial antisymmetry of the Coriolis force, and an α-effect concentrated towards the equator⁷ via an assumed latitudinal dependency α ∝ sin² θ cos θ.

Figure 6:

Radial variations of the α-effect for the two classes of mean-field models considered in Section 4.2.5. The magnetic diffusivity profile is again indicated by a dash-dotted line, and the core-envelope interface by a dotted line.

Figure 7 shows a selection of such dynamo solutions, in the form of time-latitude diagrams of the toroidal field extracted at the core-envelope interface, here r_c/R_⊙ = 0.7. If sunspot-producing toroidal flux ropes form in regions of peak toroidal field strength, and if those ropes rise radially to the surface, then such diagrams are directly comparable to the sunspot butterfly diagram of Figure 3. All models have C_Ω = 25000, |C_α| = 10, η_T/η_c = 10, and η_T = 5 × 10¹¹ cm² s⁻¹, which leads to τ ≃ 300 yr. To facilitate comparison between solutions, here antisymmetric parity was imposed via the boundary condition at the equator.

Figure 7:

Northern hemisphere time-latitude (“butterfly”) diagrams for a selection of αΩ dynamo solutions, constructed at the depth r_c/R_⊙ = 0.7 corresponding to the core-envelope interface. Isocontours of toroidal field are normalized to their peak amplitudes, and plotted for increments ΔB/max(B) = 0.2, with yellow-to-red (green-to-blue) contours corresponding to B > 0 (< 0). All but the first solution have the α-effect concentrated at the base of the envelope, with a latitude dependence as given above each panel. Other model ingredients as in Figure 5. Note the co-existence of two distinct, cycles in the solution shown in Panel B. Four corresponding animations are available in Resource 1.

Models using the radially broad, full convection zone α-effect (Panel A of Figure 7) feed mostly on the latitudinal shear in the envelope, so that the dynamo mode propagates radially upward in the envelope, with some latitudinal propagation in the tachocline only at the onset of the cycle (see animation). Models with positive C_α nonetheless yield oscillatory solutions, but those with C_α < 0 produce steady modes over a wide range of parameter values. Models using an α-effect concentrated at the base of the envelope (Panels B through D), on the other hand, are powered by the radial shear therein, and show the expected tilt in the butterfly diagrams, as expected from the Parker-Yoshimura sign rule (cf. Section 4.2.4). Note that even for an equatorially-concentrated α-effect (Panels B and D), a strong polar branch is nonetheless apparent in the butterfly diagrams, a direct consequence of the stronger radial shear present at high latitudes in the tachocline (see also corresponding animations).

It is noteworthy that co-existing dynamo branches, as in Panel B of Figure 7, can have distinct dynamo periods, which in nonlinearly saturated solutions leads to long-term amplitude modulation. This is typically not expected in dynamo models where the only nonlinearity present is a simple algebraic quenching formula such as Equation (24). A portion of the magnetic energy time-series for that solution is shown in Panel A of Figure 8 to illustrate the effect. Note that this does not occur for the C_α < 0 solution (Panel B of Figure 8), where both branches propagate away from each other, but share a common latitude of origin and so are phased-locked at the onset (cf. Panel D of Figure 7).

Figure 8:

Time series of magnetic energy in four mean-field αΩ dynamo solutions. Panels A and B show the time series associated with the solutions shown in Panels B and D of Figure 7 (base CZ, α ∼ sin²θcosθ, Cα = ±10). Note the initial phase of exponential growth of the magnetic field, followed by a saturation phase characterized here by an (atypical) periodic modulation in the case of the solution in Panel A. Panels C and D show time series for two interface dynamo solutions (see Section 4.3 and Figure 10) for two diffusivity ratios. The energy scale is expressed in arbitrary units, but is consistent across all four panels.

A common property of all oscillatory αΩ solutions discussed so far is that their period, for given values of the dynamo numbers C_α, C_Ω, is inversely proportional to the numerical value adopted for the (turbulent) magnetic diffusivity η_T. The ratio of poloidal-to-toroidal field strength, in turn, is found to scale as some power (usually close to 1/2) of the ratio C_α/C_Ω, at a fixed value of the product C_α × C_Ω.

Vector magnetograms of sunspots active regions make it possible to estimate the current helicity j · B which is closely related to the usual magnetic helicity A · B, and the amount of twist in the sunspot-forming toroidal flux ropes (see, e.g., Hagyard and Pevtsov, 1999, and references therein). Upon assuming that this current helicity reflects that of the diffuse, dynamo-generated magnetic field from which the flux ropes formed, one obtains another useful constraint on dynamo models. In the context of classical αΩ mean-field models, predominantly negative current helicity in the N-hemisphere, in agreement with observations, is usually obtained for models with negative α-effect relying primarily on positive radial shear at the equator (see Gilman and Charbonneau, 1999, and discussion therein).

The models discussed above are based on rather minimalistics and partly ad hoc assumptions on the form of the α-effect. More elaborate models have been proposed, relying on calculations of the full α-tensor based on some underlying turbulence models. While this approach usually displaces the ad hoc assumptions away from the α-effect and into the turbulence model, it has the definite advantage of offering an internally consistent approach to the calculation of turbulent diffusivities and large-scale flows. Rüdiger and Brandenburg (1995) remain a good example of the current state-of-the-art in this area; see also Rüdiger and Arlt (2003), and references therein.

4.2.6 Critical assessment

From a practical point of view, the outstanding success of the mean-field αΩ model remains its robust explanation of the observed equatorward drift of toroidal field-tracing sunspots in the course of the cycle in terms of a dynamo-wave. On the theoretical front, the model is also buttressed by mean-field electrodynamics which, in principle, offers a physically sound theory from which to compute the (critical) α-effect and magnetic diffusivity. The models’ primary uncertainties turn out to lie at that level, in that the application of the theory to the Sun in a tractable manner requires additional assumptions that are most certainly not met under solar interior conditions. Those uncertainties are exponentiated when taking the theory into the nonlinear regime, to calculate the dependence of the α-effect and diffusivity on the magnetic field strength. This latter problem remains very much open at this writing.

4.3 Interface dynamos

4.3.1 Strong α-quenching and the saturation problem

The α-quenching expression (24) used in the preceding section amounts to saying that dynamo action saturates once the mean, dynamo-generated field reaches an energy density comparable to that of the driving turbulent fluid motions, i.e., $B_{\rm eq}\sim \sqrt{4\pi\rho} \ v$, where υ is the turbulent velocity amplitude. This appears eminently sensible, since from that point on a toroidal fieldline would have sufficient tension to resist deformation by cyclonic turbulence, and so could no longer feed the α-effect. At the base of the solar convective envelope, one finds B_eq ∼ 1 kG, for υ ∼ 10³ cm s⁻¹, according to standard mixing length theory of convection. However, various calculations and numerical simulations have indicated that long before the mean field 〈B〉 reaches this strength, the helical turbulence reaches equipartition with the small-scale, turbulent component of the magnetic field (e.g., Cattaneo and Hughes, 1996, and references therein). Such calculations also indicate that the ratio between the small-scale and mean magnetic components should itself scale as Rm^1/2, where Rm = υℓ/η is a magnetic Reynolds number based on the microscopic magnetic diffusivity. This then leads to the alternate quenching expression

$$\alpha \rightarrow \alpha (\langle {\bf{B}} \rangle) = {{{\alpha _0}} \over {1 + {\rm{Rm(}}\langle {\bf{B}} \rangle/{B_{{\rm{eq}}}}{{\rm{)}}^{\rm{2}}}}},$$

(32)

known in the literature as strong α-quenching or catastrophic quenching. Since Rm ∼ 10⁸ in the solar convection zone, this leads to quenching of the α-effect for very low amplitudes for the mean magnetic field, of order 10⁻¹ G. Even though significant field amplification is likely in the formation of a toroidal flux rope from the dynamo-generated magnetic field, we are now a very long way from the 10–100 kG demanded by simulations of buoyantly rising flux ropes (see Fan, 2004).

A way out of this difficulty was proposed by Parker (1993), in the form of interface dynamos. The idea is beautifully simple: If the toroidal field quenches the α-effect, amplify and store the toroidal field away from where the α-effect is operating! Parker showed that in a situation where a radial shear and α-effect are segregated on either side of a discontinuity in magnetic diffusivity (taken to coincide with the core-envelope interface, see Panel A of Figure 9), the αΩ dynamo equations support solutions in the form of travelling surface waves localized on the discontinuity in diffusivity. The key aspect of Parker’s solution is that for supercritical dynamo waves, the ratio of peak toroidal field strength on either side of the discontinuity surface is found to scale with the diffusivity ratio as

$${{\max ({B_2})} \over {\max ({B_1})}}\sim\left({{{{\eta _2}} \over {{\eta _1}}}} \right){,^{ - 1/2}}$$

(33)

where the subscript “1” refers to the low-η region below the core-envelope interface, and “2” to the high-η region above. If one assumes that the envelope diffusivity η₂ is of turbulent origin then η₂ ∼ ℓυ, so that the toroidal field strength ratio then scales as ∼ (υℓ/η₁)^1/2 = Rm^1/2. This is precisely the factor needed to bypass strong α-quenching (Charbonneau and MacGregor, 1996). Somewhat more realistic variations on Parker’s basic models were later elaborated (MacGregor and Charbonneau (1997); Zhang et al. (2004), see also Panels B and C of Figure 9), and, while differing in important details, nonetheless confirmed Parker’s overall picture.

Figure 9:

Three interface dynamo models in semi-infinite Cartesian geometry. In Parker’s original model, the α-effect occupies the space z > 0 and the radial shear z < 0, with the magnetic diffusivity varying discontinuously from (low) η₁ to (high) η₂ across the z = 0 surface. The MacGregor and Charbonneau model is similar, except that the shear and α-effect are spatially localized as δ-functions, located a finite distance away from z = 0 in their respective halves of the domain. The Zhang et al. model moves one step closer to the Sun by truncating vertically the Parker model, and sandwiching the dynamo layers between a vacuum layer (top) and very low diffusivity layer (bottom); this bottom layer represents the radiative core, while the shear region is then associated with the tachocline. Each one of these models supports travelling waves solutions of the form exp(ikx − wt), vertically localized about the core-envelope interface (z = 0).

Tobias (1996a) discusses in detail a related Cartesian model bounded in both horizontal and vertical direction, but with constant magnetic diffusivity η throughout the domain. Like Parker’s original interface configuration, his model includes an α-effect residing in the upper half of the domain, with a purely radial shear in the bottom half. The introduction of diffusivity quenching then reduces the diffusivity in the shear region, “naturally” turning the model into a bona fide interface dynamo, supporting once again oscillatory solutions in the form of dynamo waves travelling in the “latitudinal” x-direction. This basic model was later generalized by various authors (Tobias, 1997; Phillips et al., 2002) to include the nonlinear backreaction of the dynamo-generated magnetic field on the differential rotation; further discussion of such nonlinear models is deferred to Section 5.3.1.

4.3.2 Representative results

The next obvious step is to construct an interface dynamo in spherical geometry, using a solar-like differential rotation profile. This was undertaken by Charbonneau and MacGregor (1997). Unfortunately, the numerical technique used to handle the discontinuous variation in η at the core-envelope interface turned out to be physically erroneous for the vector potential A describing the poloidal field⁸ (see Markiel and Thomas, 1999, for a discussion of this point), which led to spurious dynamo action in some parameter regimes. The matching problem is best avoided by using a continuous but rapidly varying diffusivity profile at the core-envelope interface, with the α-effect concentrated at the base of the envelope, and the radial shear immediately below, but without significant overlap between these two source regions (see Panel B of Figure 10). Such numerical models can be constructed as a variation on the αΩ models considered earlier, and stand somewhere between Parker’s original picture (see Panel A of Figure 9) and the models with spatially localized α-effect and shear (see Panels B and C of Figure 9).

Figure 10:

A representative interface dynamo model in spherical geometry. This solution has C_Ω = 2.5 × 10⁵, C_α = +10, and a core-to-envelope diffusivity contrast of 10⁻². Panel A shows a sunspot butterfly diagram, and Panel B a series of radial cuts of the toroidal field at latitude 15°. The (normalized) radial profiles of magnetic diffusivity, α-effect, and radial shear are also shown, again at latitude 15°. The core-envelope interface is again at r/R_⊙ = 0.7 (dotted line), where the magnetic diffusivity varies near-discontinuously. Panels C and D show the variations of the core-to-envelope peak toroidal field strength and dynamo period with the diffusivity contrast, for a sequence of otherwise identical dynamo solutions. Corresponding animations are available in Resource 2.

In conjunction with a solar-like differential rotation profile, making a working interface dynamo model is markedly trickier than if only a radial shear is operating, as in the Cartesian models discussed earlier (see Charbonneau and MacGregor, 1997; Markiel and Thomas, 1999). Panel A of Figure 10 shows a butterfly diagram for a numerical interface solution with C_Ω = 2.5 × 10⁵, C_α = +10, and a core-to-envelope diffusivity contrast Δη = 10⁻². A magnetic energy time series for this solution is plotted in Panel D of Figure 8, together with a solution with a smaller diffusivity contrast Δη = 0.1 (see Panel C of Figure 8). The poleward propagating equatorial branch is precisely what one would expect from the combination of positive radial shear and positive α-effect according to the Parker-Yoshimura sign rule⁹. Here the α-effect is (artificially) concentrated towards the equator, by imposing a latitudinal dependency α ∼ sin (49) for π/4 ≤ θ ≤ 3π/4, and zero otherwise.

The model does achieve the kind of toroidal field amplification one would like to see in interface dynamos. This can be seen in Panel B of Figure 10, which shows radial cuts of the toroidal field taken at latitude π/8, and spanning half a cycle. Notice how the toroidal field peaks below the core-envelope interface (vertical dotted line), well below the α-effect region and near the peak in radial shear. Panel C of Figure 10 shows how the ratio of peak toroidal field below and above r_c varies with the imposed diffusivity contrast Δη. The dashed line is the dependency expected from Equation (33). For relatively low diffusivity contrast, −1.5 ≤ log(Δη) ≲ 0, both the toroidal field ratio and dynamo period increase as ∼ (Δη)^−1/2. Below log(Δη) ∼ −1.5, the max(B)-ratio increases more slowly, and the cycle period falls, contrary to expectations for interface dynamos (see, e.g., MacGregor and Charbonneau, 1997). This is basically an electromagnetic skin-depth effect; the cycle period is such that the poloidal field cannot diffuse as deep as the peak in radial shear in the course of a half cycle. The dynamo then runs on a weaker shear, thus yielding a smaller field strength ratio and weaker overall cycle (cf. Panels C and D of Figure 8; on the energetics of interface dynamos; see also Ossendrijver and Hoyng, 1997)

Zhang et al. (2003a) have presented results for a fully three-dimensional α²Ω interface dynamo model where, however, dynamo solutions remain largely axisymmetric when a strong shear is present in the tachocline. They use an α-effect spanning the whole convective envelope radially, but concentrated latitudinally near the equator, a core-to-envelope magnetic diffusivity contrast Δη = 10⁻¹, and the usual algebraic α-quenching formula. Unfortunately, their differential rotation profile is non-solar. However, they do find that the dynamo solutions they obtain are robust with respect to small changes in the model parameters. The next obvious step here is to repeat the calculations with a solar-like differential rotation profile.

4.3.3 Critical assessment

So far the great success of interface dynamos remains their ability to evade α-quenching even in its “strong” formulation, and so produce equipartition or perhaps even super-equipartition mean toroidal magnetic fields immediately beneath the core-envelope interface. They represent the only variety of dynamo models formally based on mean-field electrodynamics that can achieve this without additional physical effects introduced into the model. All of the uncertainties regarding the calculations of the α-effect and magnetic diffusivity carry over from αΩ to interface models, with diffusivity quenching becoming a particularly sensitive issue in the latter class of models (see, e.g., Tobias, 1996a).

Interface dynamos suffer acutely from something that is sometimes termed “structural fragility”. Many gross aspects of the model’s dynamo behavior often end up depending sensitively on what one would normally hope to be minor details of the model’s formulation. For example, the interface solutions of Figure 10 are found to behave very differently if either

• the α-effect region is displaced upwards by a mere 0.05 R_⊙, or

• the α-effect is less concentrated towards the equator, for example via the ∼ sin² θ cos θ form used in Section 4.2, or

• the tachocline thickness is increased by 50%, leading to somewhat greater overlap between the α-effect and shear source regions.

Compare also the behavior of the C_α > 0 solutions discussed here to those discussed in Markiel and Thomas (1999). Once again the culprit is the latitudinal shear. Each of these minor variations on the same basic model has the effect that a parallel mid-latitude dynamo mode, powered by the latitudinal shear within the tachocline and envelope, interferes with and/or overpowers the interface mode. This interpretation is not inconsistent with the robustness claimed by Zhang et al. (2003a), since these authors have chosen to omit the latitudinal shear throughout the convective envelope in their model. Because of this structural sensitivity, interface dynamo solutions also end up being annoyingly sensitive to choice of time-step size, spatial resolution, and other purely numerical details. From a modelling point of view, interface dynamos lack robustness.

4.4 Mean-field models including meridional circulation

Meridional circulation is unavoidable in turbulent, compressible rotating convective shells. It basically results from an imbalance between Reynolds stresses and buoyancy forces. The ∼ 15 m s⁻¹ poleward flow observed at the surface (see, e.g., Hathaway, 1996) has now been detected helioseismically, down to r/R_⊙ ≃ 0.85 (Schou and Bogart, 1998; Braun and Fan, 1998), without significant departure from the poleward direction except locally and very close to the surface, in the vicinity of active region belts (Haber et al., 2002; Basu and Antia, 2003; Zhao and Kosovichev, 2004).

Accordingly, we now add a steady meridional circulation to our basic αΩ models of Section 4.2. The convenient parametric form developed by van Ballegooijen and Choudhuri (1988) is used here and in all later illustrative models including meridional circulation (Sections 4.5 and 4.8). This parameterization defines a steady quadrupolar circulation pattern, with a single flow cell per quadrant extending from the surface down to a depth r_b. Circulation streamlines are shown in Figure 11, together with radial cuts of the latitudinal component at mid-latitudes (θ = π/4). The flow is poleward in the outer convection zone, with an equatorial return flow peaking slightly above the core-envelope interface, and rapidly vanishing below.

Figure 11:

Streamlines of meridional circulation (Panel A), together with the total magnetic diffusivity profile defined by Equation (19) (dash-dotted line) and a mid-latitude radial cut of u_θ (bottom panel). The dotted line is the core-envelope interface. This is the analytic flow of van Ballegooijen and Choudhuri (1988), with parameter values m = 0.5, p = 0.25, q = 0, and r_b = 0.675.

The inclusion of meridional circulation in the non-dimensionalized αΩ dynamo equations leads to the appearance of a new dimensionless quantity, again a magnetic Reynolds number, but now based on an appropriate measure of the circulation speed u₀:

$${\rm{Rm}}={{{u_0}{R_ \odot }} \over {{\eta _{\rm{T}}}}}.$$

(34)

Using the value u₀ = 1500 cm s⁻¹ from observations of the observed poleward surface meridional flow leads to Rm ≃ 200, again with η_T = 5 × 10¹¹ cm² s⁻¹.

4.4.1 Representative results

Meridional circulation can bodily transport the dynamo-generated magnetic field (terms labeled “advective transport” in Equations (11, 12)), and therefore, for a (presumably) solar-like equator-ward return flow that is vigorous enough — in the sense of Rm being large enough — overpower the Parker-Yoshimura propagation rule embodied in Equation (31). This was nicely demonstrated by Choudhuri et al. (1995), in the context of a mean-field αΩ model with a positive α-effect concentrated near the surface, and a latitude-independent, purely radial shear at the core-envelope interface. With a solar-like differential rotation profile, however, once again the situation is far more complex.

Starting from the three αΩ dynamo solutions with the α-effect concentrated at the base of the convective envelope, (see Figure 7, Panels B through D), new solutions are now recomputed, this time including meridional circulation. Results are shown in Figure 12, for three increasing values of the circulation flow speed, as measured by Rm. At Rm = 50, little difference is seen with the circulation-free solutions, except for the C_α = +10 solution with equatorially-concentrated α-effect (see Panel A of Figure 12), where the equatorial branch is now dominant and the polar branch has shifted to mid-latitudes and has become doubly-periodic. At Rm = 200, corresponding here to a solar-like circulation speed, drastic changes have materialized in all solutions. The negative C_α solution has now transited to a steady dynamo mode, that in fact persists to higher Rm values (panels F and I). The C_α = +10 solution with α ∝ cos θ is decaying at Rm = 200, while the solution with equatorially-concentrated α-effect starts to show a hint of equatorward propagation at mid-latitudes (Panel D). At Rm = 10³, the circulation has overwhelmed the dynamo wave, and both positive C_α solutions show equatorially-propagating toroidal fields (Panels G and H). Qualitatively similar results were obtained by Küker et al. (2001) using different prescriptions for the α-effect and solar-like differential rotation (see in particular their Figure 11; see also Rüdiger and Elstner, 2002; Bonanno et al., 2003).

Figure 12:

Time-latitude diagrams for three of the αΩ solutions depicted earlier in Panels B to D of Figure 7, except that meridional circulation is now included, with Rm = 50 (top row), Rm = 200 (middle row), and Rm = 10³ (bottom row). For the turbulent diffusivity value adopted here, η_t = 5 × 10¹¹ cm² s⁻¹, Rm = 200 corresponds to a solar-like circulation speed. Corresponding animations are available in Resource 3.

Evidently, meridional circulation can have a profound influence on the overall character of the solutions. The behavioral turnover from dynamo wave-like solutions to circulation-dominated magnetic field transport sets in when the circulation speed becomes comparable to the propagation speed of the dynamo wave. In the circulation-dominated regime, the cycle period loses sensitivity to the assumed turbulent diffusivity value, and becomes determined primarily by the circulation’s turnover time. This can be seen in Figure 12: At Rm = 50 the solutions in Panels A and B have markedly distinct (primary) cycle periods, while at Rm = 10³ (Panels G and H) the cycle periods are nearly identical. Note however that significant effects require a large Rm (≳ 10³ for the circulation profile used here), which, u₀ being fixed by surface observations, translates into a magnetic diffusivity η_T ≲ 10¹¹; by most orders-of-magnitude estimates constructed in the framework of mean-field electrodynamics this is rather low.

Meridional circulation can also dominate the spatio-temporal evolution of the radial surface magnetic field, as shown in Figure 13 for a sequence of solutions with Rm = 0, 50, and 200 (corresponding toroidal butterfly diagram at the core-envelope interface are plotted in Panel B of Figure 7 and in Panel A and D of Figure 12).

Figure 13:

Time-latitude diagrams of the surface radial magnetic field, for increasing values of the circulation speed, as measured by the Reynolds number Rm. This is an αΩ solution with the α-effect concentrated at low-latitude and at the base of the convective envelope (see Section 4.2.5 and Panel B of Figure 7). Recall that the Rm = 0 solution in Panel A exhibits amplitude modulation (cf. Panel B of Figure 7 and Panel A of Figure 8).

In the circulation-free solution (Rm = 0), the equatorward drift of the surface radial field is a direct reflection of the equatorward drift of the deep-seated toroidal field (see Panel B of Figure 7). With circulation turned on, however, the surface magnetic field is swept instead towards the pole (see Panel B of Figure 13), becoming strongly concentrated and amplified there for solar-like circulation speeds (Rm = 200, see Panel C of Figure 13).

4.4.2 Critical assessment

From the modelling point-of-view, the inclusion of meridional circulation yields a much better fit to observed surface magnetic field evolution, as well as a robust setting of the cycle period. Whether it can provide an equally robust equatorward propagation of the deep toroidal field is less clear. The results presented here in the context of mean-field αΩ models suggest a rather complex overall picture, yet in other classes of models discussed below (Sections 4.5 and 4.8), circulation does have this desired effect. The effects of envelope meridional circulation on interface dynamos (Section 4.3), however, remains unexplored.

On the other hand, dynamo models including meridional circulation invariably produce surface polar field strength largely in excess of observed values. This is direct consequence of magnetic flux conservation in the converging poleward flow. This situation carries over to the other types of models to be discussed in Sections 4.5 and 4.8, unless additional modelling assumptions are introduced (e.g., enhanced surface magnetic diffusivity, see Dikpati et al., 2004). The rather low value of the turbulent magnetic diffusivity needed to achieve high enough Rm is also somewhat problematic. A more fundamental and potential serious difficulty harks back to the kinematic approximation, whereby the form and speed of u_p is specified a priori. Meridional circulation is a relatively weak flow in the bottom half of the solar convective envelope (see Miesch, 2005), so its ability to merrily advect equipartition-strength magnetic fields should not be taken for granted.

Before leaving the realm of mean-field dynamo models it is worth noting that many of the conceptual difficulties associated with calculations of the α-effect and turbulent diffusivity are not unique to the mean-field approach, and in fact carry over to all models discussed in the following sections. In particular, to operate properly all of the upcoming solar dynamo models require the presence of a strongly enhanced magnetic diffusivity, presumably of turbulent origin, at least in the convective envelope.

4.5 Models based on shear instabilities

We now turn to a recently proposed class of dynamo models relying on the latitudinal shear instability of the angular velocity profiles in the upper radiative portion of the solar tachocline (Dikpati and Gilman, 2001). Although the study of dynamo action in this context has barely begun, results published so far (see Dikpati and Gilman, 2001; Dikpati et al., 2004) make this class of models worthy of further consideration.

4.5.1 From instability to α-effect

Dikpati and Gilman (2001) work with what are effectively the mean field αΩ dynamo equations including meridional circulation. They design their “tachocline α-effect” in the form of a latitudinal parameterization of the longitudinally-averaged kinetic helicity associated with the planforms they obtain from a linear hydrodynamical stability analysis of the latitudinal differential rotation in the part of the tachocline coinciding with the overshoot region (see Dikpati and Gilman, 2001). Figure 14 shows some typical latitudinal profiles of kinetic helicity for various model parameter settings and azimuthal wavenumbers, all computed in the framework of shallow-water theory. In analogy with mean-field theory, the resulting ±-effect is assumed to be proportional to kinetic helicity but of opposite sign (see Equation (21)), and so is here predominantly positive at mid-latitudes in the Northern solar hemisphere. In their dynamo model, Dikpati and Gilman (2001) use a solar-like differential rotation, depth-dependent magnetic diffusivity and meridional circulation pattern much similar to those shown on Figures 5, 6, and 11 herein, and the usual ad hoc ±-quenching formula (cf. Equation (24)) is introduced as the sole amplitude-limiting nonlinearity.

Figure 14:

A sample of longitudinally-averaged kinetic helicity profiles associated with the linearly unstable horizontal planforms of azimuthal order m (as indicated) in the shallow-water model of Dikpati and Gilman (2001). The parameters s₂ and s₄ control the form of the latitudinal differential rotation, and are equivalent to the parameters a₂ and a₄ in Equation (18) herein. The parameter G is a measure of stratification in the shallow-water model, with larger values of G corresponding to stronger stratification (and thus a stronger restoring buoyancy force); G ≃ 0.1 is equivalent to a subadiabaticity of ∼ 10⁻⁴ (diagram kindly provided by M. Dikpati).

4.5.2 Representative solutions

Many representative solutions for this class of dynamo models can be examined in Dikpati and Gilman (2001) and Dikpati et al. (2004), where their properties are discussed at some length. Figure 15 shows time-latitude diagrams of the toroidal field at the core-envelope interface, and surface radial field. This is a solar-like solution with a mid-latitude surface meridional (poleward) flow speed of 17 m s⁻¹, envelope diffusivity η_T = 5 × 10¹¹ cm² s⁻¹, and a core-to-envelope magnetic diffusivity contrast Δη = 10⁻³.

Figure 15:

Time-latitude “butterfly” diagrams of the toroidal field at the core-envelope interface (left), and surface radial field (right) for a representative dynamo solution computed using the model of Dikpati and Gilman (2001). Note how the deep toroidal field peaks at very low latitudes, in good agreement with the sunspot butterfly diagram. For this solution the equatorial deep toroidal field and polar surface radial field lag each other by ∼ π, but other parameter settings can bring this lag closer to the observed π/2 (diagrams kindly provided by M. Dikpati).

Note the equatorward migration of the deep toroidal field, set here by the meridional flow in the deep envelope, and the poleward migration and intensification of the surface poloidal field, again a direct consequence of advection by meridional circulation, as in the mean-field dynamo models discussed in Section 4.4 in the advection-dominated, high Rm regime. The three-lobe structure of each spatio-temporal cycle in the butterfly diagram reflects the presence of three peaks in the latitudinal profile of kinetic helicity (see Figure 14).

4.5.3 Critical assessment

While these models are only a recent addition to the current “zoo” of solar dynamo models, they have been found to compare favorably to a number of observed solar cycle features. In many cases they yield equatorward propagating dominant activity belts, solar-like cycle periods, and correct phasing between the surface polar field and the tachocline toroidal field. These features can be traced primarily to the advective action of the meridional flow. They also yield the correct solution parity, and are self-excited. Like conventional αΩ models relying on meridional circulation to set the propagation direction of dynamo waves (see Section 4.4.2), the meridional flow must remain unaffected by the dynamo-generated magnetic field at least up to equipartition strength, a potentially serious difficulty also shared by the Babcock-Leighton models discussed in Section 4.8 below.

The applicability of shallow-water theory to the solar tachocline notwithstanding, the primary weakness of these models, in their present form, is their reliance on a linear stability analysis that altogether ignores the destabilizing effect of magnetic fields. Gilman and Fox (1997) have demonstrated that the presence of even a weak toroidal field in the tachocline can very efficiently destabilize a latitudinal shear profile that is otherwise hydrodynamically stable (see also Zhang et al., 2003b). Relying on a purely hydrodynamical stability analysis is then hard to reconcile with a dynamo process producing strong toroidal field bands of alternating polarities migrating towards the equator in the course of the cycle, especially since latitudinally concentrated toroidal fields have been found to be unstable over a very wide range of toroidal field strengths (see Dikpati and Gilman, 1999). In the MHD version of the shear instability studied by P. Gilman and collaborators, the structure of the instability planforms is highly dependent on the assumed underlying toroidal field profile, so that the kinetic helicity can be expected to (i) have a time-dependent latitudinal distribution, and (ii) be intricately dependent on 〈B〉, in a manner that is unlikely to be reproduced by a simple amplitude-limiting quenching formula such as Equation (24). Linear calculations carried out to date in the framework of shallow-water MHD indicate that the purely hydrodynamical α-effect considered here is indeed strongly affected by the presence of an unstable toroidal field (see Dikpati et al., 2003). However, progress has been made in studying non-linear development of both the hydrodynamical and MHD versions of the shear instability (see, e.g., Cally, 2001; Cally et al., 2003), so that the needed improvements on the dynamo front are hopefully forthcoming.

4.6 Models based on buoyant instabilities of sheared magnetic layers

Dynamo models relying on the buoyant instability of magnetized layers have been presented in Thelen (2000b), the layer being identified with the tachocline. Here also the resulting azimuthal electromotive force is parameterized as a mean-field-like α-effect, introduced into the standard αΩ dynamo equations. The model is nonlinear, in that it includes the magnetic backreaction on the large-scale, purely radial velocity shear within the layer. The analysis of Thelen (2000a) indicates that the α-effect is negative in the upper part of the shear layer. Cyclic solutions are found in substantial regions of parameter space, and, not surprisingly, the solutions exhibit migratory wave patterns compatible with the Parker-Yoshimura sign rule.

Representative solutions for this class of dynamo models can be examined in Thelen (2000b). These models are not yet at the stage where they can be meaningfully compared with the solar cycle. They do have a number of attractive features, including their ability to operate in the strong field regime.

4.7 Models based on flux tube instabilities 4.7.1 From instability to α-effect

To date, stability studies of toroidal flux ropes stored in the overshoot layer have been carried out in the framework of the thin-flux tube approximation (Spruit, 1981). It is possible to construct “stability diagrams” taking the form of growth rate contours in a parameter space comprised of flux tube strength, latitudinal location, depth in the overshoot layer, etc. One such diagram, taken from Ferriz-Mas et al. (1994), is reproduced in Figure 16. The key is now to identify regions in such stability diagrams where weak instability arises (growth rates ≳ 1 yr). In the case shown in Figure 16, these regions are restricted to flux tube strengths in the approximate range 60–150 kG. The correlation between the flow and field perturbations is such as to yield a mean azimuthal electromotive force equivalent to a positive α-effect in the N-hemisphere (Ferriz-Mas et al., 1994; Brandenburg and Schmitt, 1998).

Figure 16:

Stability diagram for toroidal magnetic flux tubes located in the overshoot layer immediately beneath the core-envelope interface. The plot shows contours of growth rates in the latitude-field strength plane. The gray scale encodes the azimuthal wavenumber of the mode with largest growth rate, and regions left in white are stable. Dynamo action is associated with the regions with growth rates ∼ 1 yr, here labeled I and II (diagram kindly provided by A. Ferriz-Mas).

4.7.1 Representative solutions

Dynamo models relying on the non-axisymmetric buoyant instability of toroidal magnetic fields were first proposed by Schmitt (1987), and further developed by Ferriz-Mas et al. (1994); Schmitt et al. (1996), and Ossendrijver (2000a) for the case of toroidal flux tubes. These dynamo models are all mean-field-like, in that the mean azimuthal electromotive force arising from instability of the flux tubes is parametrized as an α-effect, and the dynamo equations solved are then the same as those of the conventional αΩ mean-field model (see Section 4.2.2), including various forms of algebraic α-quenching as the sole amplitude-limiting nonlinearity. As with mean-field models, the dynamo period presumably depends sensitively on the assumed value of (turbulent) magnetic diffusivity, and equatorward propagation of the dynamo wave requires a negative α-effect at low latitudes.

4.7.2 Critical assessment

Although it has not yet been comprehensively studied, this dynamo mechanism has a number of very attractive properties. It operates without difficulty in the strong field regime (in fact it requires strong fields to operate). It also naturally yields dynamo action concentrated at low latitudes, so that a solar-like butterfly diagram can be readily produced from a negative α-effect even with a solar-like differential rotation profile, at least judging from the solutions presented in Schmitt et al. (1996) and Ossendrijver (2000a,b).

Difficulties include the need of a relatively finely tuned magnetic diffusivity to achieve a solar-like dynamo period, and a relatively finely-tuned level of subadiabaticity in the overshoot layer for the instability to kick on and off at the appropriate toroidal field strengths (compare Figures 1 and 2 in Ferriz-Mas et al., 1994). The non-linear saturation of the instability is probably less of an issue here than with the α-effect based on purely hydrodynamical shear instability (see Section 4.5 above), since, as the instability grows, the flux ropes leave the site of dynamo action by entering the convection zone and buoyantly rising to the surface.

The effects of meridional circulation in this class of dynamo models has yet to be investigated; this should be particularly interesting, since both analytic calculations and numerical simulations suggest a positive α-effect in the Northern hemisphere, which should then produce poleward propagation of the dynamo wave at low latitude. Meridional circulation could then perhaps produce equatorward propagation of the dynamo magnetic field even with a positive α-effect, as it does in true mean-field models (cf. Section 4.4). At any rate, further studies of dynamo models relying on this poloidal field regeneration mechanism should be vigorously pursued.

4.8 Babcock-Leighton models

Solar cycle models based on what is now called the Babcock-Leighton mechanism were first proposed by Babcock (1961) and further elaborated by Leighton (1964, 1969), yet they were all but eclipsed by the rise of mean-field electrodynamics in the mid- to late 1960’s. Their revival was motivated not only by the mounting difficulties with mean-field models alluded to earlier, but also by the fact that synoptic magnetographic monitoring over solar cycles 21 and 22 has offered strong evidence that the surface polar field reversals are indeed triggered by the decay of active regions (see Wang et al., 1989; Wang and Sheeley Jr, 1991, and references therein). The crucial question is whether this is a mere side-effect of dynamo action taking place independently somewhere in the solar interior, or a dominant contribution to the dynamo process itself.

The mode of operation of a generic solar cycle model based on the Babcock-Leighton mechanism is illustrated in cartoon form in Figure 17. Let P_n represent the amplitude of the high-latitude, surface (“A”) poloidal magnetic field in the late phases of cycle n, i.e., after the polar field has reversed. The poloidal field P_n is advected downward by meridional circulation (A→B), where it then starts to be sheared by the differential rotation while being also advected equatorward (B→C). This leads to the growth of a new low-latitude (C) toroidal flux system T_n+1, which becomes buoyantly unstable (C→D) and starts producing sunspots (D) which subsequently decay and release the poloidal flux P_n+1 associated with the new cycle n +1. Poleward advection and accumulation of this new flux at high latitudes (D→A) then obliterates the old poloidal flux P_n, and the above sequence of steps begins anew. Meridional circulation clearly plays a key role in this “conveyor belt” model of the solar cycle, by providing the needed link between the two spatially segregated source regions.

Figure 17:

Operation of a solar cycle model based on the Babcock-Leighton mechanism. The diagram is drawn in a meridional quadrant of the Sun, with streamlines of meridional circulation plotted in blue. Poloidal field having accumulated in the surface polar regions (“A”) at cycle n must first be advected down to the core-envelope interface (dotted line) before production of the toroidal field for cycle n + 1 can take place (B→C). Buoyant rise of flux rope to the surface (C→D) is a process taking place on a much shorter timescale.

4.8.1 Formulation of a poloidal source term

As with all other dynamo models discussed thus far, the troublesome ingredient in dynamo models relying on the Babcock-Leighton mechanism is the specification of an appropriate poloidal source term, to be incorporated into the mean-field axisymmetric dynamo equations. In essence, all implementations discussed here are inspired by the results of numerical simulations of the buoyant rise of thin flux tubes, which, in principle allow to calculate the emergence latitude and tilts of BMRs, which is at the very heart of the Babcock-Leighton mechanism.

The first post-helioseismic dynamo model based on the Babcock-Leighton mechanism is due to Wang et al. (1991); these authors developed a coupled two-layer model (2 × 1D), where a poloidal source term is introduced in the upper (surface) layer, and made linearly proportional to the toroidal field strength at the corresponding latitude in the bottom layer. A similar non-local approach was later used by Dikpati and Charbonneau (1999) and Charbonneau et al. (2005) in their fully 2D axisymmetric model implementation, using a solar-like differential rotation and meridional flow profiles similar to Figures 5 and 11 herein. The otherwise much similar implementation of Nandy and Choudhuri (2001, 2002), on the other hand, uses a mean-field-like local α-effect, concentrated in the upper layers of the convective envelope and operating in conjunction with a “buoyancy algorithm” whereby toroidal fields located at the core-envelope interface are locally removed and deposited in the surface layers when their strength exceed some preset threshold. The implementation developed by Durney (1995) is probably closest to the essence of the Babcock-Leighton mechanism (see also Durney et al., 1993; Durney, 1996, 1997); whenever the deep-seated toroidal field exceeds some preset threshold, an axisymmetric “double ring” of vector potential is deposited in the surface layer, and left to spread latitudinally under the influence of magnetic diffusion.

In all cases the poloidal source term is concentrated in the outer convective envelope, and, in the language of mean-field electrodynamics, amounts to a positive α-effect, in that a positive dipole moment is being produced from a positive deep-seated mean toroidal field. The Dikpati and Charbonneau (1999) and Nandy and Choudhuri (2001) source terms both have an α-quenching-like upper operating threshold on the toroidal field strength. This is motivated by simulations of rising thin flux tubes, indicating that tubes with strength in excess of about 100 kG emerge without the E-W tilt required for the Babcock-Leighton mechanism to operate. The Durney (1995), Nandy and Choudhuri (2001), and Charbonneau et al. (2005) implementations also have a lower operating threshold, as suggested by thin flux tubes simulations.

4.8.2 Representative results

Figure 18 shows N-hemisphere time-latitude diagrams for the toroidal magnetic field at the core-envelope interface (Panel A), and the surface radial field (Panel B), for a representative Babcock-Leighton dynamo solution computed following the model implementation of Dikpati and Charbonneau (1999). The equatorward advection of the toroidal field by meridional circulation is here clearly apparent, as well as the concentration of the surface radial field near the pole. Note how the polar radial field changes from negative (blue) to positive (red) at just about the time of peak positive toroidal field at the core-envelope interface; this is the phase relationship inferred from synoptic magnetograms (see, e.g., Figure 4 herein) as well as observations of polar faculae (see Sheeley Jr, 1991).

Figure 18:

Time-latitude diagrams of the surface toroidal field at the core-envelope interface (Panel A), and radial component of the surface magnetic field (Panel B) in a Babcock-Leighton model of the solar cycle. This solution is computed for solar-like differential rotation and meridional circulation, the latter here closing at the core-envelope interface. The core-to-envelope contrast in magnetic diffusivity is Δη = 1/300, the envelope diffusivity η_T = 2.5 × 10¹¹ cm² s⁻¹, and the (poleward) mid-latitude surface meridional flow speed is u₀ = 16 m s⁻¹.

Although it exhibits the desired equatorward propagation, the toroidal field butterfly diagram in Panel A of Figure 18 peaks at much higher latitude (∼ 45°) than the sunspot butterfly diagram (∼ 15° −20°, cf. Figure 3). This occurs because this is a solution with high magnetic diffusivity contrast, where meridional circulation closes at the core-envelope interface, so that the latitudinal component of differential rotation dominates the production of the toroidal field. This difficulty can be alleviated by letting the meridional circulation penetrate below the core-envelope interface. Solutions with such flows are presented, e.g., in Dikpati and Charbonneau (1999) and Nandy and Choudhuri (2001, 2002). These latter authors have argued that this is in fact essential for a solar-like butterfly diagram to materialize, but this conclusion appears to be model-dependent at least to some degree (Guerrero and Muñoz, 2004), and others have failed to reproduce some of their numerical results (see Dikpati et al., 2005), leaving the issue somewhat muddled at this juncture. At any rate, Babcock-Leighton dynamo solutions often do tend to produce strong polar branches, a consequence of both the strong radial shear present in the high-latitude portion of the tachocline, and of the concentration of the poloidal field taking place in the high latitude-surface layer prior to this field being advected down into the tachocline by meridional circulation (viz. Figure 17)

A noteworthy property of this class of model is the dependency of the cycle period on model parameters; over a wide portion of parameter space, the meridional flow speed is found to be the primary determinant of the cycle period P. For example, in the Dikpati and Charbonneau (1999) model, this quantity is found to scale as

$$P = 56.8 \, u_0^{- 0.89}s_0^{- 0.13}\eta _{\rm{T}}^{0.22}\;\;[{\rm{yr}}].$$

(35)

This behavior arises because, in these models, the two source regions are spatially segregated, and the time required for circulation to carry the poloidal field generated at the surface down to the tachocline is what effectively sets the cycle period. The corresponding time delay introduced in the dynamo process has rich dynamical consequences, to be discussed in Section 5.4 below.

Note finally that the weak dependency of P on η_T and on the magnitude s₀ of the poloidal source term is very much unlike the behavior typically found in mean-field models, where both these parameters play a dominant role in setting the cycle period.

4.8.3 Critical assessment

As with most models including meridional circulation published to date, Babcock-Leighton dynamo models usually produce excessively strong polar surface magnetic fields. While this difficulty can be fixed by increasing the magnetic diffusivity in the outermost layers, in the context of the Babcock-Leighton models this then leads to a much weaker poloidal field being transported down to the tachocline, which can be problematic from the dynamo point-of-view. On this see Dikpati et al. (2004) for illustrative calculations, and Mason et al. (2002) on the closely related issue of competition between surface and deep-seated α-effect.

Because of the strong amplification of the surface poloidal field in the poleward-converging meridional flow, Babcock-Leighton models tend to produce a significant — and often dominant — polar branch in the toroidal field butterfly diagram. Many of the models explored to date tend to produce symmetric-parity solutions when computed pole-to-pole over a full meridional plane (see, e.g., Dikpati and Gilman, 2001), but it is not clear how serious a problem this is, as relatively minor changes to the model input ingredients may flip the dominant parity (see, e.g., Chatterjee et al., 2004, for a specific, if physically curious, example).

Because the Babcock-Leighton mechanism is characterized by a lower operating threshold, the resulting dynamo models are not self-excited. On the other hand, the Babcock-Leighton mechanism is expected to operate even for toroidal fields exceeding equipartition, the main uncertainties remaining the level of amplification taking place when sunspot-forming toroidal flux ropes form from the dynamo-generated mean magnetic field.

The nonlinear behavior of this class of models, at the level of magnetic backreaction on the differential rotation and meridional circulation, remains unexplored.

4.9 Numerical simulations of solar dynamo action

Ultimately, the solar dynamo problem should be tackled as a (numerical) solution of the complete set of MHD partial differential equations in a rotating, spherical domain undergoing thermally-driven turbulent convection in its outer 30% in radius. It is a peculiar fact that the last full-fledged attempts to do so go back some some twenty years, to the simulations of Gilman and Miller (1981); Gilman (1983); Glatzmaier (1985a,b), despite the remarkable advances in computational capabilities having taken place in the intervening years.

These epoch-making simulations did produce cyclic dynamo action and latitudinal migratory patterns suggestive of the dynamo waves of mean-field theory. However, the associated differential rotation profile turned out non-solar, as did the magnetic field’s spatio-temporal evolution. In retrospect this is perhaps not surprising, as limitations in computing resources forced the simulations to be carried out in a parameter regime far removed from solar interior conditions. Since then and until recently, efforts on the full-sphere simulation front have gone mostly into the purely hydrodynamical problem of reproducing the large-scale flows in the solar convective envelope, as inferred by helioseismology (see, e.g., Miesch, 2005, and references therein). However, the recent numerical simulations of Brun et al. (2004) have reached a strongly turbulent regime, and have managed to produce a reasonably strong mean magnetic field, but without equatorward migration or polarity reversals. These authors suggest that these failings can be traced to the absence of a tachocline-like stable region of strong shear at the bottom of their simulation domain. If this is the case, then direct numerical simulation of the solar cycle will turn out to be even more demanding computationally than hitherto believed.

A number of attempts have also been made to reproduce some salient features of the solar cycle by carrying out high-resolution, local simulations in parameters regimes closer to solar-like (see, e.g., Nordlund et al., 1992; Tobias et al., 2001; Ossendrijver et al., 2002). One issue that has received much attention in the past decade is the interaction of a turbulent, convecting fluid (“convection zone”) with a shear flow concentrated in an underlying stably stratified “tachocline” region (see, e.g., Brummell et al., 2002). Such simulations have shown that magnetic fields can be pumped into the stable regions by convective downdrafts, and produce elongated structures reminiscent of magnetic flux tubes aligned with the flow. The recent simulations of Cline et al. (2003) are particularly interesting in this respect, as they have managed to produce sustained, reasonably regular cyclic activity with occasional polarity reversals for extended periods of simulation time. At first sight this may look superficially like an αΩ dynamo, but the turbulent flow has no net helicity since rotation is not included in the simulations; the poloidal field is not being regenerated by a mean-field-like turbulent α-effect, but rather by the interaction between buoyancy and the Kelvin-Helmholtz instability in the shear layer. Such fascinating numerical experiments must clearly be pursued.

5 Amplitude Fluctuations, Multiperiodicity, and Grand Minima

Given that the basic physical mechanism(s) underlying the operation of the solar cycle are not yet agreed upon, attempting to understand the origin of the observed fluctuations of the solar cycle may appear to be a futile undertaking. Nonetheless, work along these lines continues at full steam in part because of the high odds involved; it is becoming increasingly accepted that varying levels of solar activity may contribute significantly to climate change (see Beer et al., 2000; Reid, 2000, and references therein). Moreover, the frequencies of all eruptive phenomena relevant to space weather are strongly modulated by the amplitude of the solar cycle. Finally, certain aspects of the observed fluctuations may actually hold important clues as to the physical nature of the dynamo process.

5.1 The observational evidence: An overview

Panel A of Figure 19 shows a time series of the so-called Zürich sunspot numbers, starting in the mid-eighteenth century and extending to the present. The thin line is the monthly sunspot number, and the red line a 13-month running mean thereof. The 11-year sunspot cycle is the most obvious feature of this time series, although the period of the underlying magnetic cycle is in fact twice that (sunspot counts being insensitive to magnetic polarity). Since sunspots are a surface manifestation of the toroidal magnetic flux system residing in the solar interior, cycle-to-cycle variations in sunspot counts are usually taken to indicate a corresponding variation in the amplitude of the Sun’s dynamo-generated internal magnetic field. As reasonable as this may sound, it remains a working assumption; at this writing, the process via which the dynamo-generated mean magnetic field produces sunspot-forming concentrated flux ropes is not understood. One should certainly not take for granted that a difference by a factor of two in sunspot count indicates a corresponding variation by a factor of two in the strength of the internal magnetic field; it is not even entirely clear whether the two are monotonically related.

Figure 19:

Fluctuations of the solar cycle, as measured by the sunspot number. Panel A is a time series of the Zürich monthly sunspot number (with a 13-month running mean in red). Cycles are numbered after the convention introduced in the mid-nineteenth century by Rudolf Wolf. Note how cycles vary significantly in both amplitude and duration. Panel B is a portion of the ¹⁰Be time series spanning the Maunder Minimum (data courtesy of J. Beer). Panel C shows a time series of the yearly group sunspot number of Hoyt and Schatten (1998) (see also Hathaway et al., 2002) over the same time interval, together with the yearly Zuürich sunspot number (purple) and auroral counts (green). Panels D and E illustrate the pronounced anticorrelation between cycle amplitude and rise time (Waldmeier Rule), and alternance of higher-than-average and lower-that-average cycle amplitudes (Gnevyshev-Ohl Rule, sometimes also referred to as the “odd-even effect”).

At any rate, the notion of a nicely regular 11/22-year cycle does not hold long upon even cursory scrutiny, as the amplitude of successive cycles is clearly not constant, and their overall shape often differs significantly from one cycle to another (cf. cycles 14 and 15 in Panel A of Figure 19). Closer examination of Figure 19 also reveals that even the cycle’s duration is not uniform, spanning in fact a range going from 9 yr (cycle 2) to nearly 14 yr (cycle 4). These amplitude and duration variations are not a sunspot-specific artefact; similar variations are in fact observed in other activity proxies with extended records, most notably the 10.7 cm radio flux (Tapping, 1987), polar faculae counts (Sheeley Jr, 1991), and the cosmogenic radioisotopes ¹⁴C and ¹⁰Be (Beer et al., 1991; Beer, 2000).

Equally striking is the pronounced dearth of sunspots in the interval 1645–1715 (see Panel C of Figure 19); this is not due to lack of observational data (see Ribes and Nesme-Ribes, 1993; Hoyt and Schatten, 1996), but represents instead a phase of strongly suppressed activity now known as the Maunder Minimum (Eddy, 1976, 1983, and references therein). Evidence from cosmogenic radioisotopes indicates that similar periods of suppressed activity have taken place in ca. 1282–1342 (Wolf Minimum) and ca. 1416–1534 (Spöorer Minimum), as well as a period of enhanced activity in ca. 1100–1250 (the Medieval Maximum).

The various incarnations of the sunspot number time series (monthly SSN, 13-month smoothed SSN, yearly SSN, etc.) are arguably the most intensely studied time series in astrophysics, as measured by the number of published research paper pages per data points. Various correlations and statistical trends have been sought in these datasets. Panel D of Figure 19 and Panel E of Figure 19 present two such classical trends. The “Waldmeier Rule”, illustrated in Panel D of Figure 19, refers to a statistically significant anticorrelation between cycle amplitude and rise time (linear correlation coefficient r = −0.68). A similar anticorrelation exists between cycle amplitude and duration, but is statistically more dubious (r = −0. 37). The “Gnevyshev-Ohl” rule, illustrated in Panel E of Figure 19, refers to a marked tendency for odd (even) numbered cycles to have amplitudes above (below) their running mean (blue line in Panel E of Figure 19), a pattern that seems to have held true without interruption between cycles 9 and 21 (see also Mursula et al., 2001).

A number of long-timescale modulations have also been extracted from these data, most notably the so-called Gleissberg cycle (period = 88 yr), but the length of the sunspot number record is insufficient to firmly establish the reality of these periodicities. One must bring into the picture additional solar cycle proxies, primarily cosmogenic radioisotopes, but difficulties in establishing absolute amplitudes of production rates introduce additional uncertainties into what is already a complex endeavour (for more on these matters, see Beer, 2000; Usoskin and Mursula, 2003). Likewise, the search for chaotic modulation in the sunspot number time series has produced a massive literature (see, e.g., Feynman and Gabriel, 1990; Mundt et al., 1991; Carbonell et al., 1994; Rozelot, 1995, and references therein), but without really yielding firm, statistically convincing conclusions, again due to the insufficient lengths of the datasets.

The aim in this section is to examine in some detail the types of fluctuations that can be produced in the various dynamo models discussed in the preceding section¹⁰. After going briefly over the potential consequences of fossil fields (Section 5.2), dynamical nonlinearities are first considered (Section 5.3), followed by time-delay effects (Section 5.4). We then turn to stochastic forcing (Section 5.5), which leads naturally to the issue of intermittency (Section 5.6).

5.2 Fossil fields and the 22-yr cycle

The presence of a large-scale, quasi-steady magnetic field of fossil origin in the solar interior has long been recognized as a possible explanation of the Gnevyshev-Ohl rule (see Panel E of Figure 19). The basic idea is quite simple: The slowly-decaying, deep fossil field being effectively steady on solar cycle timescales, its superposition with the 11-yr polarity reversal of the overlying dynamogenerated field will lead to a 22-yr modulation, whereby the cycle is stronger when the fossil and dynamo field have the same polarity, and weaker when these polarities are opposite (see, e.g., Boyer and Levy, 1984; Boruta, 1996). The magnitude of the effect is directly related to the strength of the fossil field, versus that of the dynamo-generated magnetic field. All of this, however, presumes that flows and dynamical effects within the tachocline still allow “coupling” between the deep fossil field below, and the cyclic dynamo-generated field above. It is far from obvious that this coupling could indeed take place in the simple manner implicitly assumed in dynamo models, that typically incorporate the effect of fossil fields via the lower boundary condition.

One strong prediction is associated with this explanation of the Gnevyshev-Ohl rule: While the pattern may become occasionally lost due to large amplitude fluctuations of other origin, whenever it is present even-numbered cycles should always be of lower amplitudes and odd-numbered cycles of higher amplitude (under Wolf’s cycle numbering convention). Evidently, this prediction can be tested observationally, provided one can establish a measure of sunspot cycle amplitude that is truly characteristic of the strength of the underlying dynamo magnetic field. Taken at face value, the analysis of Mursula et al. (2001), based on cycle-integrated group sunspot numbers, indicates that the odd/even pattern has reversed between the time periods 1700–1800 and 1850–1990 (see their Figure 1). This would then rule out the fossil field hypothesis unless, as argued by some authors (see Usoskin et al., 2001, and references therein), a sunspot cycle has been “lost” around 1790, at the onset of the so-called Dalton minimum. For more on these matters, see Section 6 in Usoskin and Mursula (2003).

5.3 Dynamical nonlinearity

5.3.1 Backreaction on large-scale flows

The dynamo-generated magnetic field will, in general, produce a Lorentz force that will tend to oppose the driving fluid motions. This is a basic physical effect that should be included in any dynamo model. It is not at all trivial to do so, however, since in a turbulent environment both the fluctuating and mean components of the magnetic field can affect both the large-scale flow components, as well as the small-scale turbulent flow providing the Reynolds stresses powering the large-scale flows. One can thus distinguish a number of (related) amplitude-limiting mechanisms:

• Lorentz force associated with the mean magnetic field directly affecting large-scale flow (sometimes called the “Malkus-Proctor effect”, after the groudbreaking numerical investigations of Malkus and Proctor (1975)).

• Large-scale magnetic field indirectly affecting large-scale flow via effects on small-scale turbulence and associated Reynolds stresses (sometimes called “Λ-quenching”, see, e.g., Kitchatinov and Rüdiger, 1993).

• Maxwell stresses of small-scale magnetic field directly or indirectly affecting large-scale flow.

The α-quenching formulae introduced in Section 4.2.1 is a particularly simple — some would say simplistic — way to model the backreaction of the magnetic field on the turbulent fluid motions producing the α-effect¹¹. In the context of solar cycle models, one could also expect the Lorentz force to reduce the amplitude of differential rotation until the effective dynamo number falls back to its critical value, at which point the dynamo again saturates¹². The third class of quenching mechanism listed above has not yet been investigated in detail, but numerical simulations of MHD turbulence indicate that the effects of the small-scale turbulent magnetic field on the α-effect can be profound (see Pouquet et al., 1976; Durney et al., 1993).

Introducing magnetic backreaction on differential rotation is a tricky business, because one must then also, in principle, provide a model for the Reynolds stresses powering the large-scale flows in the solar convective envelope (see, e.g., Kitchatinov and Rüdiger, 1993), as well as a procedure for computing magnetic backreaction on these. This rapidly leads into the unyielding realm of MHD turbulence, although algebraic “Λ-quenching” formulae akin to α-quenching have been proposed based on specific turbulence models (see, e.g., Kitchatinov et al., 1994). Alternately, one can add an ad hoc source term to the right hand side of Equation (2), designed in such a way that in the absence of the magnetic field, the desired solar-like large-scale flow is obtained. As a variation on this theme, one can simply divide the large-scale flow into two components, the first (U) corresponding to some prescribed, steady profile, and the second (U′) to a time-dependent flow field driven by the Lorentz force (see, e.g., Tobias, 1997; Moss and Brooke, 2000; Thelen, 2000b):

$${\bf{u}} = {\bf{U}}({\bf{x}}) + {{\bf{U}}^{\prime}}({\bf{x}}, t, \langle {\bf{B}} \rangle),$$

(36)

with the (non-dimensional) governing equation for U′ including only the Lorentz force and a viscous dissipation term on its right hand side. If u amounts only to differential rotation, then U′ must obey a (nondimensional) differential equation of the form

$${{\partial {{\bf{U}}^{\prime}}} \over {\partial t}} = {\Lambda \over {4\pi \rho }}(\nabla \times \langle {\bf{B}} \rangle) \times \langle {\bf{B}} \rangle + {{\rm{P}}_{\rm{m}}}{\nabla ^2}{\bf{U}}$$

(37)

where time has been scaled according to the magnetic diffusion time $\tau=R_{\odot}^{2}/\eta_{\rm T}$ as before. Two dimensionless parameters appear in Equation (37). The first (Λ) is a numerical parameter measuring the influence of the Lorentz force, and which can be set to unity without loss of generality (cf. Tobias, 1997; Phillips et al., 2002). The second, P_m = ν/η, is the magnetic Prandtl number. It measures the relative importance of viscous and Ohmic dissipation. When P_m ≪ 1, large velocity amplitudes in U′ can be produced by the dynamo-generated mean magnetic field. This effectively introduces an additional, long timescale in the model, associated with the evolution of the magnetically-driven flow; the smaller P_m, the longer that timescale (cf. Figures 4 and 10 in Brooke et al., 1998).

The majority of studies published thus far and using this approach have only considered the nonlinear magnetic backreaction on differential rotation. This has been shown to lead to a variety of behaviors, including amplitude and parity modulation, periodic or aperiodic, as well as intermittency (more on the latter in Section 5.6). Knobloch et al. (1998) have argued that amplitude modulation in such models can be divided into two main classes. Type-I modulation corresponds to a nonlinear interaction between modes of different parity, with the Lorenz force-mediated flow variations controlling the transition from one mode to another. Type-II modulation refers to an exchange of energy between a single dynamo mode (of some fixed parity) with the flow field. This leads to quasiperiodic modulation of the basic cycle, with the modulation period controlled by the magnetic Prandtl number. Both types of modulation can co-exists in a given dynamo model, leading to a rich overall dynamical behavior.

Figure 20 shows two butterfly diagrams produced by the nonlinear mean-field interface model of Tobias (1997) (see also Beer et al., 1998). The model is defined on a Cartesian slab with a reference differential rotation varying only with depth, and includes backreaction on the differential rotation according to the procedure described above. The model exhibits strong, quasi-periodic modulation of the basic cycle, leading to epochs of strongly reduced amplitude. Note how the dynamo can emerge from such epochs with strong hemispheric asymmetries (top panel), or with a different parity (bottom panel).

Figure 20:

Amplitude and parity modulation in a dynamo model including magnetic backreaction on the differential rotation. These are the usual time-latitude diagrams for the toroidal magnetic field, now covering both solar hemispheres, and exemplify the two basic types of modulation arising in nonlinear dynamo models with backreaction on the differential rotation (see text; figure kindly provided by S.M. Tobias).

It is not clear, at this writing, to what degree these behaviors are truly generic, as opposed to model-dependent. The analysis of Knobloch et al. (1998) suggests that generic behaviors do exist. On the other hand, a number of counterexamples have been published, showing that even in a qualitative sense, the nonlinear behavior can be strongly dependent on what one would have hoped to be minor modelling details (see, e.g., Moss and Brooke, 2000; Phillips et al., 2002).

The differential rotation can also be suppressed indirectly by magnetic backreaction on the small-scale turbulent flows that produce the Reynolds stresses driving the large-scale mean flow. Inclusion of this so-called “Λ-quenching” in mean-field dynamo models, alone or in conjunction with other amplitude-limiting nonlinearities, has also been shown to lead to a variety of periodic and aperiodic amplitude modulations, provided the magnetic Prandtl number is small (see Küker et al., 1999; Pipin, 1999). This type of models stand or fall with the turbulence model they use to compute the various mean-field coefficients, and it is not yet clear which aspects of the results are truly generic to Λ-quenching.

To date, dynamical backreaction on large-scale flows has only been studied in dynamo models based on mean-field electrodynamics. Equivalent studies must be carried out in the other classes of solar cycle models discussed in Section 4. In particular, it is essential to estimate the effect of the Lorentz force on meridional circulation in models based on the Babcock-Leighton mechanism and/or hydrodynamical instabilities in the tachocline, since in these models the circulation is the primary determinant of the cycle period and enforces equatorward propagation in the butterfly diagram. Even though meridional circulation in the convective envelope is a “weak” flow, in the sense of being much slower than differential rotation, it arises from a small imbalance between forces that are in themselves quite large; the importance of magnetically-mediated backreaction on meridional circulation is likely to be a complex affair.

5.3.2 Dynamical α-quenching

A number of authors have attempted to bypass the shortcomings of α-quenching by introducing into dynamo models an additional, physically-inspired partial differential equation for the α-coefficient itself (e.g., Kleeorin et al., 1995; Blackman and Brandenburg, 2002, and references therein). The basic physical idea is that magnetic helicity must be conserved in the high-Rm regime, so that production of helicity in the mean field implies a corresponding production of helicity of opposite sign at the scales of the fluctuating components of the flow and field, which ends up acting in such a way as to reduce the α-effect. Most investigations published to date have made used of severely truncated models, and/or models in one spatial dimensions (see, e.g., Weiss et al., 1984; Schmalz and Stix, 1991; Jenning and Weiss, 1991; Roald and Thomas, 1997; Covas et al., 1997; Blackman and Brandenburg, 2002), so that the model results can only be compared to solar data in some general qualitative sense. Rich dynamical behavior definitely arises in such models, including multiperiodicity, amplitude modulation, and chaos.

Covas et al. (1998) have incorporated dynamical α-quenching into a two-dimensional spherical axisymmetric mean-field dynamo model, and compared the resulting behavior to that produced by classical algebraic α-quenching. These authors found, perhaps not surprisingly, both quantitative and qualitative differences between solutions computed using dynamical rather than algebraic α-quenching, with the nonlinear behavior in the former case depending sensitively on model parameters, so it is not clear which class of models can be considered “more realistic”.

5.4 Time-delay dynamics

The introduction of ad hoc time-delays in dynamo models is long known to lead to pronounced cycle amplitude fluctuations (see, e.g., Yoshimura, 1978). Models including nonlinear backreaction on differential rotation can also exhibit what essentially amounts to time-delay dynamics in the low Prandtl number regime, with the large-scale flow perturbations lagging behind the Lorentz force because of inertial effects. Finally, time-delay effects can arise in dynamo models where the source regions for the poloidal and toroidal magnetic components are spatially segregated. This is a type of time delay we now turn to, in the context of dynamo models based on the Babcock-Leighton mechanism.

5.4.1 Time-delays in Babcock-Leighton models

It was already noted that in solar cycle models based on the Babcock-Leighton mechanism of poloidal field generation, meridional circulation effectively sets — and even regulates — the cycle period (cf. Section 4.8.2; see also Dikpati and Charbonneau, 1999; Charbonneau and Dikpati, 2000). In doing so, it also introduces a long time delay in the dynamo mechanism, “long” in the sense of being comparable to the cycle period. This delay originates with the time required for circulation to advect the surface poloidal field down to the core-envelope interface, where the toroidal component is produced (A→C in Figure 17). In contrast, the production of poloidal field from the deep-seated toroidal field (C→D), is a “fast” process, growth rates and buoyant rise times for sunspot-forming toroidal flux ropes being of the order of a few months (see Moreno-Insertis, 1986; Fan et al., 1993; Caligari et al., 1995, and references therein). The first, long time delay turns out to have important dynamical consequences.

5.4.2 Reduction to an iterative map

The long time delay inherent in B-L models of the solar cycle allows a formulation of cycle-to-cycle amplitude variations in terms of a simple one-dimensional iterative map (Durney, 2000; Charbonneau, 2001). Working in the kinematic regime, neglecting resistive dissipation, and in view of the conveyor belt argument of Section 4.8, the toroidal field strength T_n+1 at cycle n +1 is assumed to be linearly proportional to the poloidal field strength P_n of cycle n, i.e.,

$${T_{n + 1}} = a{P_n}.$$

(38)

Now, because flux eruption is a fast process, the strength of the poloidal field at cycle n + 1 is (nonlinearly) proportional to the toroidal field strength of the current cycle:

$${P_{n + 1}} = f({T_{n + 1}}){T_{n + 1}}.$$

(39)

Here the “Babcock-Leighton” function f (T_n+1) measures the efficiency of surface poloidal field production from the deep-seated toroidal field. Substitution of Equation (38) into Equation (39) leads immediately to a one-dimensional iterative map,

$${p_{n + 1}} = \alpha f({p_n}){p_n},$$

(40)

where the p_n’s are normalized amplitudes, and the normalization constants as well as the constant a in Equation (38) have been absorbed into the definition of the map’s parameter a, here operationally equivalent to a dynamo number (see Charbonneau, 2001). We consider here the following nonlinear function,

$$f(p) = {1 \over 4}\left[ {1 + {\rm{erf}}\left({{{p - {p_1}} \over {{w_1}}}} \right)} \right]\left[ {1 - {\rm{erf}}\left({{{p - {p_2}} \over {{w_2}}}} \right)} \right],$$

(41)

with p₁ = 0.6, w₁ = 0.2, p₂ = 1.0, and w₂ = 0.8. This catches an essential feature of the B-L mechanism, namely the fact that it can only operate in a finite range of toroidal field strength.

A bifurcation diagram for the resulting iterative map is presented in Panel A of Figure 21. For a given value of the map parameter a, the diagram gives the locus of the amplitude iterate p_n for successive n values. The “critical dynamo number” above which dynamo action becomes possible, corresponds here to α = 0.851 (p_n = 0 for smaller α values). For 0.851 ≤ α ≤ 1.283, the iterate is stable at some finite value of p_n, which increases gradually with α. This corresponds to a constant amplitude cycle. As α reaches 1.283, period doubling occurs, with the iterate p_n alternating between high and low values (e.g., p_n = 0.93 and p_n = 1.41 at α = 1.4). Further period doubling occurs at α = 1.488, then at α = 1.531, then again at α = 1.541, and ever faster until a point is reached beyond which the amplitude iterate seems to vary without any obvious pattern (although within a bounded range); this is in fact a chaotic regime.

Figure 21:

Two bifurcation diagrams for a kinematic Babcock-Leighton model, where amplitude fluctuations are produced by time-delay feedback. The top diagram is computed using the one-dimensional iterative map given by Equations (40, 41), while the bottom diagram is reconstructed from numerical solutions in spherical geometry, of the type discussed in Section 4.8. The shaded area in Panel A maps the attraction basin for the cyclic solutions, with initial conditions located outside of this basin converging to the trivial solution p_n = 0.

As in any other dynamo model where the source regions for the poloidal and toroidal magnetic field components are spatially segregated, the type of time delay considered here is unavoidable. The B-L model is just a particularly clear-cut example of such a situation. One is then led to anticipate that the map’s rich dynamical behavior should find its counterpart in the original, arguably more realistic spatially-extended, diffusive axisymmetric model that inspired the map formulation. Remarkably, this is indeed the case.

Panel B of Figure 21 shows a bifurcation diagram, conceptually equivalent to that shown in Panel A, but now constructed from a sequence of numerical solutions of the Babcock-Leighton model discussed earlier in Section 4.8, for increasing values of the dynamo number in that model. Time series of magnetic energy were calculated from the numerical solutions, and successive peaks found and plotted for each individual solution. The sequence of period doubling, eventually leading to a chaotic regime, is strikingly similar to the bifurcation diagram constructed from the corresponding iterative map, down to the narrow multiperiodic windows interspersed in the chaotic domain. This demonstrates that time delay effects are a robust feature, and represent a very powerful source of cycle amplitude fluctuation in Babcock-Leighton models, even in the kinematic regime (for further discussion see Charbonneau, 2001; Charbonneau et al., 2005).

5.5 Stochastic forcing

Another means of producing amplitude fluctuations in dynamo models is to introduce stochastic forcing in the governing equations. Sources of stochastic “noise” certainly abound in the solar interior; large-scale flows in the convective envelope, such as differential rotation and meridional circulation, are observed to fluctuate, an unavoidable consequence of dynamical forcing by the surrounding, vigorous turbulent flow. Ample observational evidence now exists that a substantial portion of the Sun’s surface magnetic flux is continuously being reprocessed on a timescale commensurate with convective motions (see Schrijver et al., 1997; Hagenaar et al., 2003). The culprit is most likely the generation of small-scale magnetic fields by these turbulent fluid motions (see, e.g., Cattaneo, 1999; Cattaneo et al., 2003, and references therein). This amounts to a form of zero-mean “noise” superimposed on the slowly-evolving mean magnetic field. These mechanisms can be thought of as physical noise. In addition, the azimuthal averaging implicit in all models of the solar cycle considered above will yield dynamo coefficients showing significant deviations about their mean values, as a consequence of the spatio-temporally discrete nature of the physical events (e.g., cyclonic updrafts, sunspot emergences, flux rope destabilizations, etc.) whose collective effects add up to produce a mean electromotive force. Such time-dependent, statistical deviations about the mean can be dubbed statistical noise.

Physical noise is most readily incorporated into dynamo models by introducing, on the right hand side of the governing equations, an additional zero-mean source term that varies randomly from node to node and from one time step to the next. Statistical noise can be modeled in a number of ways. Perhaps the most straightforward is to let the dynamo number fluctuate randomly in time about some pre-set mean value. By most statistical estimates, the expected magnitude of these fluctuations is quite large, i.e., many times the mean value (Hoyng, 1988, 1993). This conclusion is also supported by numerical simulations (see, e.g., Otmianowska-Mazur et al., 1997; Ossendrijver et al., 2001). One typically also introduces a coherence time during which the dynamo number retains a fixed value. At the end of this time interval, this value is randomly readjusted. Depending on the dynamo model at hand, the coherence time can be related to the lifetime of convective eddies (α-effect-based mean-field models), to the decay time of sunspots (Babcock-Leighton models), or to the growth rate of instabilities (hydrodynamical shear or buoyant MHD instability-based models). Perhaps not surprisingly, the level of cycle amplitude fluctuations is found to increase with both increasing noise amplitude and longer coherence time (Choudhuri, 1992).

Figure 22 shows some representative results for three αΩ dynamo solutions with fluctuation in the dynamo number C_α ranging from ±50% (blue) to ±200% (red). While the correlation time amounts here to only 5% of the half-cycle period, note in Panel A of Figure 22 how modulations on much longer timescales appear in the magnetic energy time series. As can be seen in Panel B of Figure 22, the fluctuations also lead to a spread in the cycle period, although here little (anti)correlation is seen with the cycle’s amplitude. Both the mean cycle period and amplitude increase with increasing fluctuation amplitude.

Figure 22:

Stochastic fluctuations of the dynamo number in an αΩ mean-field dynamo solution. The reference, unperturbed solution is the same as that plotted in Panel D of Figure 7, except that is uses a lower value for the dynamo number, Cα = −5. Panel A shows magnetic energy time series for three solutions with increasing fluctuation amplitudes, while Panel B shows a correlation plot of cycle amplitude and duration, as extracted from a time series of the toroidal field at the core-envelope interface (r/R = 0.7) in the model. Solutions are color-coded according to the relative amplitude (δC_α/C_α of the fluctuations in the dynamo number. Line segments in Panel B indicate the mean cycle amplitudes and durations for the three solutions. The correlation time of the noise amounts here to about 5% of the mean half-cycle period in all cases.

The effect of noise has been investigated in most detail in the context of mean-field models (see Choudhuri, 1992; Hoyng, 1993; Ossendrijver and Hoyng, 1996; Ossendrijver et al., 1996; Mininni and Gómez, 2002, 2004). A particularly interesting consequence of random variations of the dynamo number, in mean-field models at or very close to criticality, is the coupling of the cycle’s duration and amplitude (Hoyng, 1993; Ossendrijver and Hoyng, 1996; Ossendrijver et al., 1996), leading to a pronounced anticorrelation between these two quantities that is reminiscent of the Waldmeier Rule (cf. Panel D of Figure 19), and hard to produce by purely nonlinear effects (cf. Ossendrijver and Hoyng, 1996). However, this behavior does not carry over to the supercritical regime, so it is not clear whether this can indeed be accepted as a robust explanation of the observed amplitude-duration anticorrelation. In the supercritical regime, α-quenched mean-field models are less sensitive to noise (Choudhuri, 1992), unless of course they happen to operate close to a bifurcation point, in which case large amplitude and/or parity fluctuations can be produced (see, e.g., Moss et al., 1992).

In the context of Babcock-Leighton models, Charbonneau and Dikpati (2000) have presented a series of dynamo simulations including fluctuations in the dynamo number (statistical noise) as well as fluctuations in the meridional circulation (a form of noise both physical and statistical). Working in the supercritical regime with a form of algebraic α-quenching as the sole amplitude-limiting nonlinearity, they find the model solutions to be quite robust with respect to the introduction of noise, and succeed in producing a solar-like weak anticorrelation between cycle amplitude and duration for fluctuations in the dynamo numbers in excess of 200% of its mean value, with coherence time of one month. They also find that the solutions exhibit good phase locking, in that shorter-than-average cycles tend to be followed by longer-than-averaged cycles, a property they trace to the regulatory effects of meridional circulation, the primary determinant of the cycle period in these models (cf. Section 4.8 herein).

5.6 Intermittency

5.6.1 The Maunder Minimum and intermittency

The term “intermittency” was originally coined to characterize signals measured in turbulent fluids, but has now come to refer more generally to systems undergoing apparently random, rapid switching from quiescent to bursting behaviors, as measured by the magnitude of some suitable system variable (see, e.g., Platt et al., 1993). Intermittency thus requires at least two distinct dynamical states available to the system, and a means of transiting from one to the other.

In the context of solar cycle model, intermittency refers to the existence of quiescent epochs of strongly suppressed activity randomly interspersed within periods of “normal” cyclic activity. Observationally, the Maunder Minimum is usually taken as the exemplar for such quiescent epochs. It should be noted, however, that dearth of sunspots does not necessarily mean a halted cycle; as noted earlier, flux ropes of strengths inferior to ∼ 10 kG will not survive their rise through the convective envelope, and the process of flux rope formation from the dynamo-generated mean magnetic field may itself be subjected to a threshold in field strength. The same basic magnetic cycle may well have continued unabated all the way through the Maunder Minimum, but at an amplitude just below one of these thresholds. This idea finds support in the ¹⁰Be radioisotope record, which shows a clear and uninterrupted cyclic signal through the Maunder Minimum (see Panels B and C of Figure 19; also Beer et al., 1998). Strictly speaking, thresholding a variable controlled by a single dynamical state subject to amplitude modulation is not intermittency, although the resulting time series for the variable may well look quite intermittent.

Ossendrijver and Covas (2003) list 21 papers reporting empirical observation of intermittency-like behavior in one or another dynamo model, a bibliographical list that would not be particularly useful to replicate here. Research is also underway to categorize the observed behavior in terms of the various types of intermittency known to characterize dynamical systems (see, e.g., Covas and Tavakol, 1999; Brooke et al., 2002; Ossendrijver and Covas, 2003). In what follows, we attempt to pin down the physical origin of intermittent behavior in the various types of solar cycle models discussed earlier.

5.6.2 Intermittency from stochastic noise

Intermittency has been shown to occur through stochastic fluctuations of the dynamo number in mean-field dynamo models operating at criticality (see, e.g., Hoyng, 1993). Such models also exhibit a solar-like anticorrelation between cycle amplitude and phase. This mechanism for “on-off intermittency” is not as gratuitous a procedure as it may first appear. As argued in Section 5.5, important stochastic fluctuations are indeed likely in the turbulent environment in which the solar dynamo operates. However there is no strong reason to believe that the solar dynamo is running just at criticality, so that it is not clear how good an explanation this is of Maunder-type Grand Minima.

Mininni and Gómez (2004) have presented a stochastically-forced 1D (in latitude) αΩ mean-field model, including algebraic α-quenching as the amplitude-limiting nonlinearity, that exhibits a form of intermittency arising from the interaction of dynamo modes of opposite parity. The solution aperiodically produces episodes of markedly reduced cycle amplitude, and often showing strong hemispheric asymmetry. This superficially resembles the behavior associated with the type I amplitude nonlinear modulation discussed in Section 5.3.1 (compare the top panel in Figure 20 herein to Figure 7 in Mininni and Gómez (2004)). However, here it is the stochastic forcing that occasionally excites the higher-order modes that perturb the normal operation of the otherwise dominant dynamo mode.

5.6.3 Intermittency from nonlinearities

Another way to trigger intermittency in a dynamo model is to let nonlinear dynamical effects, for example a reduction of the differential rotation amplitude, push the effective dynamo number below its critical value; dynamo action then ceases during the subsequent time interval needed to reestablish differential rotation following the diffusive decay of the magnetic field; in the low P_m regime, this time interval can amount to many cycle periods, but P_m must not be too small, otherwise Grand Minima become too rare (see, e.g., Küker et al., 1999). Values P_m ∼ 10⁻² seem to work best. Such intermittency is most readily produced when the dynamo is operating close to criticality. For representative models exhibiting intermittency of this type, see Tobias (1996b, 1997); Brooke et al. (1998); Küker et al. (1999); Brooke et al. (2002).

Intermittency of this nature has some attractive properties as a Maunder Minimum scenario. First, the strong hemispheric asymmetry in sunspots distributions in the final decades of the Maunder Minimum (Ribes and Nesme-Ribes, 1993) can occur naturally via parity modulation (see Figure 20 herein). Second, because the same cycle is operating at all times, cyclic activity in indicators other than sunspots (such as radioisotopes, see Beer et al., 1998) is easier to explain; the dynamo is still operating and the solar magnetic field is still undergoing polarity reversal, but simply fails to reach the amplitude threshold above which the sunspot-forming flux ropes can be generated from the mean magnetic field, or survive their buoyant rise through the envelope.

There are also important difficulties with this explanatory scheme. Grand Minima tend to have similar durations and recur in periodic or quasi-periodic fashion, while the sunspot and radioisotope records, taken at face value, suggest a pattern far more irregular. Moreover, the dynamo solutions in the small P_m regime are characterized by large, non-solar angular velocity fluctuations. In such models, solar-like, low-amplitude torsional oscillations do occur, but for P_m ∼ 1. Unfortunately, in this regime the solutions then lack the separation of timescales needed for Maunder-like Grand Minima episodes. One is stuck here with two conflicting requirements, neither of which easily evaded.

Intermittency has also been observed in strongly supercritical model including α-quenching as the sole amplitude-limiting nonlinearity. Such solutions can enter Grand Minima-like epochs of reduced activity when the dynamo-generated magnetic field completely quenches the α-effect. The dynamo cycle restarts when the magnetic field resistively decays back to the level where the α-effect becomes operational once again. The physical origin of the “long” timescale governing the length of the “typical” time interval between successive Grand Minima episodes is unclear, and the physical underpinning of intermittency harder to identify. For representative models exhibiting intermittency of this type, see Tworkowski et al. (1998).

5.6.4 Intermittency from threshold effects

Intermittency can also arise naturally in dynamo models characterized by a lower operating threshold on the magnetic field. These include models where the regeneration of the poloidal field takes place via the MHD instability of toroidal flux tubes (Sections 4.7 and 3.2.3). In such models, the transition from quiescent to active phases requires an external mechanism to push the field strength back above threshold. This can be stochastic noise (see, e.g., Schmitt et al., 1996), or a secondary dynamo process normally overpowered by the “primary” dynamo during active phases (see Ossendrijver, 2000a). Figure 23 shows one representative solution of the latter variety, where intermittency is driven by a weak α-effect-based kinematic dynamo operating in the convective envelope, in conjunction with magnetic flux injection into the underlying region of primary dynamo action by randomly positioned downflows (see Ossendrijver, 2000a, for further details). The top panel shows a sample trace of the toroidal field, and the bottom panel a butterfly diagram constructed near the core-envelope interface in the model.

Figure 23:

Intermittency in a dynamo model based on flux tube instabilities (cf. Sections 3.2.3 and 4.7). The top panel shows a trace of the toroidal field, and the bottom panel is a butterfly diagram covering a shorter time span including a quiescent phase at 9.6 ≲ t ≲ 10.2, and a “failed minimum” at t ≃ 11 (figure produced from numerical data kindly provided by M. Ossendrijver).

The model does produce irregularly-spaced quiescent phases, as well as an occasional “failed minimum” (e.g., at t ≃ 11), in qualitative agreement with the solar record. Note here how the onset of a Grand Minimum is preceded by a gradual decrease in the cycle’s amplitude, while recovery to normal, cyclic behavior is quite abrupt. The fluctuating behavior of this promising class of dynamo models clearly requires further investigation.

5.6.5 Intermittency from time delays

Dynamo models exhibiting amplitude modulation through time-delay effects are also liable to show intermittency in the presence of stochastic noise. This was demonstrated in Charbonneau (2001) in the context of Babcock-Leighton models, using the iterative map formalism described in Section 5.4.2. The intermittency mechanism hinges on the fact that the map’s attractor has a finite basin of attraction (indicated by gray shading in Panel A of Figure 21). Stochastic noise acting simultaneously with the map’s dynamics can then knock the solution out of this basin of attraction, which then leads to a collapse onto the trivial solution p_n = 0, even if the map parameter remains supercritical. Stochastic noise eventually knocks the solution back into the attractor’s basin, which signals the onset of a new active phase (see Charbonneau, 2001, for details).

A corresponding behavior was subsequently found in a spatially-extended model similar to that described in Section 4.8 (see Charbonneau et al., 2004). Figure 24 shows one such representative solution, in the same format as Figure 23. This is a dynamo solution which, in the absence of noise, operates in the singly-periodic regime. Stochastic noise is added to the vector potential $A\hat{{\bf e}}_{\phi}$ in the outermost layers, and the dynamo number is also allowed to fluctuate randomly about a pre-set mean value. The resulting solution exhibits both amplitude fluctuations and intermittency.

Figure 24:

Intermittency in a dynamo model based on the Babcock-Leighton mechanism (cf. Sections 3.2.4 and 4.8). The top panel shows a trace of the toroidal field sampled at (r, θ) = (0.7, π/3). The bottom panel is a time-latitude diagram for the toroidal field at the core-envelope interface (numerical data from Charbonneau et al. (2004)).

With its strong polar branch often characteristic of dynamo models with meridional circulation, Figure 24 is not a particularly good fit to the solar butterfly diagram. Yet its fluctuating behavior is solar-like in a number of ways, including epochs of alternating higher-than-average and lower-than-average cycle amplitudes (the Gnevyshev-Ohl rule, cf. Panel E of Figure 19), and residual pseudocyclic variations during quiescent phases, as suggested by ¹⁰Be data, cf. Panel B of Figure 19. This later property is due at least in part to meridional circulation, which continues to advect the (decaying) magnetic field after the dynamo has fallen below threshold (see Charbonneau et al., 2004, for further discussion). Note also in Figure 24 how the onset of Grand Minima is quite sudden, while recovery to normal activity is more gradual, which is the opposite behavior to the Grand Minima in Figure 23.

6 Open Questions and Current Trends

I close this review with the following discussion of a few open questions that, in my opinion, bear particularly heavily on our understanding (or lack thereof) of the solar cycle.

6.1 What is the primary poloidal field regeneration mechanism?

Given the amount of effort having gone into building detailed dynamo models of the solar cycle, it is quite sobering to reflect upon the fact that the physical mechanism responsible for the regeneration of the poloidal component of the solar magnetic field has not yet been identified with confidence. As discussed at some length in Section 4, current models relying on distinct mechanisms all have their strengths and weaknesses, in terms of physical underpinning as well as comparison with observations.

Modelling of the evolution of the Sun’s surface magnetic flux has abundantly confirmed that the Babcock-Leighton mechanism is operating on the Sun, in the sense that magnetic flux liberated by the decay of tilted bipolar active regions does accumulate in the polar regions, where it triggers polarity reversal of the poloidal component (see Wang and Sheeley Jr, 1991; Schrijver et al., 2002; Wang et al., 2002; Baumann et al., 2004, and references therein). The key question is whether this is an active component of the dynamo cycle, or a mere side-effect of active region decay. Likewise, the buoyant instability of magnetic flux tubes (Section 4.7) is, in some sense, unavoidable; here again the question is whether or not the associated azimuthal mean electromotive force contributes significantly to dynamo action in the Sun.

Petrovay (2000) makes an interesting proposal, namely that one would be better off to categorize dynamo models according to the following two criteria: (i) whether or not the source regions for the poloidal and toroidal components are spatially coincident, and (ii) whether the sunspot butterfly diagram is to be understood in terms of the Parker-Yoshimura sign rule, or to advection by meridional circulation. All dynamo models described above fall into one of four possible categories (see Table 1 in Petrovay, 2000, and accompanying discussion). The challenge is then to devise observational criteria allowing to meaningfully distinguish between these four possible classes.

A noteworthy contribution along these lines is the recent work of Hathaway et al. (2003), who have shown that the duration of individual sunspot cycles is inversely correlated with the slope of the dynamo wave in the butterfly diagram. The latter, in models relying on advection by meridional circulation, is itself expected to be set by the equatorward meridional flow speed at the core-envelope interface, which can be related to the observable surface meridional flow speed via the mass conservation constraint; although uncertainties remain at that level, the analysis of Hathaway et al. (2003) supports the idea that the cycle period is indeed set by the meridional flow speed (but do see Schmitt and Schüssler, 2004, for an opposing viewpoint). This kind of work must be pursued.

6.2 What limits the amplitude of the solar magnetic field?

The amplitude of the dynamo-generated magnetic field is almost certainly restricted by the back-reaction of Lorentz forces on the driving fluid motions. However, as outlined in Section 5.3.1, this backreaction can occur in many ways.

Helioseismology has revealed only small variations of the differential rotation profile in the course of the solar cycle. The observed variations amount primarily to an extension in depth of the pattern of low-amplitude torsional oscillations long known from surface Doppler measurements (but see also Basu and Antia, 2001; Toomre et al., 2003). Taken at face value, these results suggest that quenching of differential rotation is not the primary amplitude-limiting mechanism, unless the dynamo is operating very close to criticality. Once again the hope is that in the not-too-distant future, helioseismology will have mapped accurately enough cycle-induced variations of differential rotation in the convective envelope and tachocline, to settle this issue. It is also worth noting that mechanisms for generating torsional oscillations that are not directly relying on the Lorentz force are also possible (see Spruit, 2003).

Algebraic quenching of the α-effect (or α-effect-like source terms) is the mechanism most often incorporated in dynamo models. However, this state of affairs usually has much more to do with computational convenience than commitment to a specific physical quenching mechanism. There is little doubt that the α-effect will be affected once the mean magnetic field reaches equipartition; the critical question is whether it becomes quenched long before that, for example by the small-scale component of the magnetic field. The issue hinges on helicity conservation and subtleties of flow-field interaction in MHD turbulence, and remains open at this writing. For recent entry points into this very active area of current research, see Cattaneo and Hughes (1996); Blackman and Field (2000); Brandenburg and Dobler (2001).

Magnetic fields are buoyantly unstable in the convective envelope, and so will rise to the surface on time scales much shorter than the cycle period (see, e.g., Parker, 1975; Schüssler, 1977; Moreno-Insertis, 1983, 1986). This is in fact the primary reason why most contemporary dynamo models of the solar cycle rely on the velocity shear in the tachocline to achieve toroidal field amplification. If the dynamo were to reside entirely in the convective envelope, then this would be an important, perhaps even dominant, amplitude limiting mechanism (see Schmitt and Schüssler, 1989; Moss et al., 1990). If, on the other hand, toroidal field amplification takes place primarily at or beneath the core-envelope interface, then it is less clear whether or not this mechanism plays a dominant role, but this remains to be confirmed by detailed calculations.

A related question is whether the destabilization, rise and surface emergence of sunspot-forming toroidal flux ropes amounts to magnetic flux loss; the answer depends on the fate of the emerged portion of the flux ropes, namely if and how it disconnects from the deep-seated magnetic flux system. Because some stretching can also take place in the course of the buoyant rise across the convective envelope, it may even be that rising flux ropes amplify the deep-seated magnetic field, as nicely demonstrated by the numerical calculations of Rempel and Schüssler (2001). Estimates of the total magnetic flux emerging at the surface of the Sun in the course of a solar cycle also amount to a small fraction of the amount of magnetic flux produced in the tachocline, for most current solar dynamo models. This suggests that flux loss due to buoyant rise of toroidal flux ropes is not the dominant amplitude-limiting mechanism.

6.3 Flux tubes versus diffuse fields

The foregoing discussion has implicitly assumed that the dynamo process produces a mean, large-scale magnetic field that then concentrates itself into the flux ropes that subsequently give rise to sunspots. High-resolution observations of the photospheric magnetic field show that even outside of sunspots, the field is concentrated in flux tubes (see, e.g., Parker, 1982, and references therein), presumably as a consequence of convective collapse of magnetic flux concentrations too weak to block convection and form sunspots. In this picture, which is basically the framework of all dynamo models discussed above, the mean magnetic field is the dominant player in the cycle.

An alternate viewpoint is to assume that the solar magnetic field is a fibril state from beginning to end, throughout the convection zone and tachocline, and that whatever large-scale field there may be in the photosphere is a mere by-product of the decay of sunspots and other flux tube-like small-scale magnetic structures. The challenge is then to devise a dynamo process that operates entirely on flux tubes, rather than on a diffuse mean field. Some exploratory calculations have been made (e.g., DeLuca et al., 1993), but this intriguing question has received far less attention than it deserves.

6.4 How constraining is the sunspot butterfly diagram?

The shape of the sunspot butterfly diagram (see Figure 3) continues to play a dominant constraining role in many dynamo models of the solar cycle. Yet caution is in order on this front. Calculations of the stability of toroidal flux ropes stored in the overshoot region immediately beneath the core-envelope interface indicate that instability is much harder to produce at high latitudes, primarily because of the stabilizing effect of the magnetic tension force; thus strong fields at high latitudes may well be there, but not produce sunspots. Likewise, the process of flux rope formation from the dynamo-generated mean magnetic field is currently not understood. Are flux ropes forming preferentially in regions of most intense magnetic fields, in regions of strongest magnetic helicity, or in regions of strongest hydrodynamical shear? Is a stronger diffuse toroidal field forming more strongly magnetized flux ropes, or a larger number of flux ropes always of the same strength?

These are all profound questions from the point of view of comparing results from dynamo models to sunspot data. Until they have been answered, uncertainty remains as to the degree to which the sunspot butterfly diagram can be compared in all details to time-latitude diagrams of the toroidal field at the core-envelope interface, as produced by this or that dynamo model.

6.5 Is meridional circulation crucial?

The main question regarding meridional circulation is not whether it is there or not, but rather what role it plays in the solar cycle. The answer hinges on the value of the turbulent diffusivity nT, which is notoriously difficult to estimate with confidence. It is probably essential in dynamo models characterized by positive α-effects in the Northern hemisphere, in order to ensure equator-ward transport of the sunspot-forming, deep-seated toroidal magnetic field (see Sections 4.4, 4.5, and 4.7). It also appears to be a major determinant in the evolution of the large-scale surface magnetic field in the course of the solar cycle. Something like it is certainly needed in dynamo models based on the Babcock-Leighton mechanism, to carry the poloidal field generated at the surface down to the tachocline, where production of the toroidal field is taking place (see Section 4.8). In the context of Babcock-Leighton models, meridional circulation has also been shown to act as a clock regulating the pace of the solar cycle (Charbonneau and Dikpati, 2000), and favoring phase persistence across intermittent, quiescent epochs of suppressed activity (Charbonneau et al., 2004), in qualitative agreement with inferences from cosmogenic radioisotopes studies.

The primary unknown at this writing is the degree to which meridional circulation is affected by the Lorentz force associated with the dynamo-generated magnetic field. Recent calculations by M. Rempel and collaborators (Rempel, 2004) suggest that the backreaction is limited to regions of strongest toroidal fields, so that the “conveyor belt” is still operating in the bulk of the convective envelope. Such calculations must be vigorously pursued.

Another pressing matter is to establish the form and speed of the equatorward return flow in the lower convective envelope, and to determine how much — if any — penetration takes place in the radiative layers below. While Nandy and Choudhuri (2002) have argued that deep penetration (i.e., down to r/R_⊙ ≃ 0.6) is essential for a proper butterfly diagram to be produced, the boundary layer analysis of Gilman and Miesch (2004) indicates no significant penetration below the base of the convective envelope. This is an issue where the final word will likely come from helioseismology, hopefully in the not too distant future.

6.6 Is the mean solar magnetic field really axisymmetric?

While the large-scale solar magnetic field is axisymmetric about the Sun’s rotation axis to a good first approximation, various lines of observational evidence point to a persistent, low-level non-axisymmetric component; such evidence includes the so-called active longitudes (see Henney and Harvey, 2002, and references therein), rotationally-based periodicity in cycle-related eruptive phenomena (Bai, 1987), and the shape of the white-light corona in the descending phase of the cycle.

Various mean-field-based dynamo models are known to support non-axisymmetric modes over a substantial portion of their parameter space (see, e.g., Moss, 1999; Bigazzi and Ruzmaikin, 2004, and references therein). At high Rm, strong differential rotation (in the sense that C_Ω ≫ C_α) is known to favor axisymmetric modes, because it efficiently destroys any non-axisymmetric component on a timescale much faster than diffusive (∝ Rm^1/3 at high Rm, instead of ∝ Rm). Although it is not entirely clear that the Sun’s differential rotation is strong enough to place it in this regime (see, e.g., Rüdiger and Elstner, 1994), some 3D models do show this symmetrizing effect of differential rotation (see, e.g., Zhang et al., 2003a).

While all poloidal field regeneration mechanisms considered above must rely on some break of axisymmetry to circumvent Cowling’s theorem, some are of a fundamentally non-axisymmetric nature even at the largest scales. This is the case with the α-effect based on both the buoyant instability of toroidal magnetic flux tubes (see Section 4.7), and on the hydrodynamical shear instability in the tachocline (see Section 4.5). In either cases stability analyses indicate that the most readily excited modes have low azimuthal wave numbers (m = 1 or m = 2). This is subsumed in an axisymmetric dynamo model upon invoking azimuthal averaging, which amounts to assuming that successive destabilization events are uncorrelated in longitude; if they are, however, then the corresponding α-effect should be itself longitude-dependent, which is known to favor the excitation of non-axisymmetric dynamo modes (see, e.g., Moss et al., 1991). This avenue should definitely be explored.

6.7 What causes Maunder-type Grand Minima?

The origin of Grand Minima in solar activity is also a question subjected to intense scrutiny. Broadly speaking, Grand Minima can occur either through amplitude modulation of a basic underlying dynamo cycle, or through intermittency. In this latter case, the transition from one state to another can take place via the system’s internal dynamics, or through the influence of external stochastic noise, or both. Not surprisingly, a large number of plausible Grand Minima models can now be found in the extant literature (cf. Section 5.6).

Historical researches have shown that the Sun climbed out of the Maunder Minimum gradually, and showing strongly asymmetric activity, with nearly all sunspots observed between 1670 and 1715 located in the Southern solar hemisphere (see Ribes and Nesme-Ribes, 1993). This is the kind of pattern that is readily produced by nonlinear modulation of two dynamo modes of comparable period but opposite parity (cf. Figure 20 herein; see also Beer et al., 1998; Sokoloff and Nesme-Ribes, 1994). Then again, in the context of an intermittency-based model, it is quite conceivable that one hemisphere can pull out of a quiescent epoch before the other, thus yielding sunspot distributions compatible with the aforecited observations in the late Maunder Minimum. Such scenarios, relying on cross-hemispheric coupling, have hardly begun to be explored.

Another possible avenue for distinguishing between these various scenarios is the persistence of the primary cycle’s phase through Grand Minima. Generally speaking, models relying on amplitude modulation can be expected to exhibit good phase persistence across such minima, because the same basic cycle is operating at all times (cf. Figure 20). Intermittency, on the other hand, should not necessarily lead to phase persistence, since the active and quiescent phases are governed by distinct dynamics. One noteworthy exception to these expectations is the intermittent Babcock-Leighton solution presented in Charbonneau et al. (2004), where the cycle’s phase can be sustained across Grand Minima, through the regulating influence of meridional circulation. One can but hope that careful analysis of cosmogenic radioisotope data may soon indicate the degree to which the solar cycle’s phase persisted through the Maunder, Spöorer, and Wolf Grand Minima, in order to narrow down the range of possibilities.

7 Resources

Resource 1: Four animations corresponding to the solutions whose butterfly diagrams are plotted on the four panels of Fig. 7

http://solarphysics.livingreviews.org/lrsp-2005-2/resources/index.html#aosolns

Resource 2: Four animations corresponding to some of the solutions whose characteristics are presented on Fig. 10, namely those with a core-to-envelope diffusivity ratio of 0.1, 0.01, 0.001 and 0.0001.

http://solarphysics.livingreviews.org/lrsp-2005-2/resources/index.html#intrf

Resource 3: Animations corresponding to the solutions whose butterfly diagrams are plotted on the nine panels of Fig. 12 (animations are not provided for the decaying and steady solutions).

http://solarphysics.livingreviews.org/lrsp-2005-2/resources/index.html#aocmsolns