The FIP and Inverse FIP Effects in Solar and Stellar Coronae

Abstract

We review our state of knowledge of coronal element abundance anomalies in the Sun and stars. We concentrate on the first ionization potential (FIP) effect observed in the solar corona and slow-speed wind, and in the coronae of solar-like dwarf stars, and the “inverse FIP” effect seen in the corona of stars of later spectral type; specifically M dwarfs. These effects relate to the enhancement or depletion, respectively, in coronal abundance with respect to photospheric values of elements with FIP below about 10 eV. They are interpreted in terms of the ponderomotive force due to the propagation and/or reflection of magnetohydrodynamic waves in the chromosphere. This acts on chromospheric ions, but not neutrals, and so can lead to ion-neutral fractionation.

A detailed description of the model applied to closed magnetic loops, and to open field regions is given, accounting for the observed difference in solar FIP fractionation between the slow and fast wind. It is shown that such a model can also account for the observed depletion of helium in the solar wind. The helium depletion is sensitive to the chromospheric altitude where ion-neutral separation occurs, and the behavior of the helium abundance in the closed magnetic loop strongly suggests that the waves have a coronal origin. This, and other similar inferences may be expected to have a strong bearing on theories of solar coronal heating.

Chromospheric waves originating from below as acoustic waves mode convert, mainly to fast-mode waves, can also give rise to ion-neutral separation. Depending on the geometry of the magnetic field, this can result in FIP or Inverse FIP effects. We argue that such configurations are more likely to occur in later-type stars (known to have stronger field in any case), and that this explains the occurrence of the Inverse FIP effect in M dwarfs. We conclude with a discussion of possible directions for future work.

1 Introduction

Working during the early years of solar UV and X-ray spectroscopy, Pottasch (1963) found evidence for significantly higher abundances of Mg, Si, and Fe in the low solar corona than in the photosphere, and concluded, somewhat reluctantly that “the chemical composition in the solar atmosphere differs from the photosphere to the corona”. These elements, Mg, Si, and Fe, are all elements with first ionization potential (FIP) less than 10 eV, now known to be routinely enhanced in abundance in the corona with respect to photospheric values, a phenomenon that has become known as the “FIP effect”. High FIP elements such as O, Ne, and He, have much smaller abundance enhancements, or even abundance depletions in the corona. Although the possibility of elemental fractionation between the solar photosphere and corona only really began to be taken seriously in the mid 1980s, with the publication of influential reviews by Meyer (1985a,b), recognizing the work of Pottasch (1963) almost fifty years ago makes the problem of understanding the FIP effect nearly as old as that of coronal heating. In fact, modern models of the effect to be discussed in detail below, in which the fractionation is driven by the ponderomotive force of Alfvén waves, make an intimate connection between the abundance anomaly and coronal heating mechanisms, such that the FIP effect may yield several important insights into the nature of the latter. This is a theme we will develop throughout this review.

The solar FIP effect manifests itself in several modes of observation. Spectroscopy, as pioneered by Pottasch (1963) and extensively reviewed at intervals over the last 20 years (e.g., Feldman, 1992; Feldman and Laming, 2000; Feldman and Widing, 2003; Saba, 1995), reveals the composition primarily of the “closed loop” corona. Meyer (1985a,b) also considered elemental abundances measured in situ in the solar wind, and in solar energetic particle events, which flow out along open magnetic field lines. Observations with Ulysses, the first mission to fly over the solar polar regions (Wenzel et al., 1992) revealed FIP fractionation varying with wind speed (Zurbuchen et al., 1999; von Steiger et al., 2000). Slow speed solar wind had abundances resembling those in the closed loop solar corona, whereas high speed wind from polar coronal holes had a much lower level of FIP fractionation. With the advent of the Solar and Heliospheric Observatory (SOHO), a more coherent observational picture began to emerge. Coronal holes, the source of the relatively unfractionated fast solar wind, were themselves shown to have similar abundances to the wind emanating from them. The lower latitude closed field corona was also shown to have FIP fractionated plasma, similar to the slow speed solar wind. Schmelz et al. (2012) give a modern view of coronal element abundances derived from these various solar physics sources, coronal spectroscopy, solar wind and solar energetic particles.

Astrophysical EUV and X-ray spectroscopy, made possible by the 1990’s launches of the Extreme Ultraviolet Explorer (EUVE), the Advanced Satellite for Cosmology and Astrophysics (ASCA), Chandra and XMM-Newton, allowed coronal abundances in stars to be measured for the first time. Again, nearly two decades after the first such observations, various observations seem to be falling into place. In this review, we will attempt to synthesize these two strands of observations, solar and stellar, into one complete picture of coronal element abundance anomalies.

Following this introduction, in Section 2 we briefly review recent developments in solar photospheric abundances, where improved spectroscopic data and the application of 3D radiation transfer calculations have ushered in a revised solar composition. Section 3 describes the various facets of the solar FIP effect, while Section 4 surveys stellar FIP and Inverse FIP effects. Section 5 describes early attempts to model the solar FIP effect. Section 6 lays out the model advocated here, where the ponderomotive force due to Alfvén waves propagating through, or reflecting from, the chromosphere accelerates ions up or down, while leaving neutral atoms unaffected. Section 7 describes the results of such a model, and discusses its important implications. Section 8 concludes with suggestion for future research directions.

2 Solar Photospheric Composition

2.1 Review

Any work on solar coronal abundance anomalies must begin with reviewing the photospheric composition. Despite its long history, the composition of the photosphere, also taken as a proxy for “cosmic abundances”, has undergone significant revisions in recent years. We take as our starting point the composition review of Anders and Grevesse (1989), this being the standard solar composition in use for the early studies of the FIP effect, and for many years the default abundance set implemented by spectral fitting software in use in X-ray astronomy. This was updated by Grevesse and Sauval (1998), who revised downwards by a small amounts N and O (0.13 and 0.10 dex, respectively) and also Fe which moved from 7.67 (on a logarithmic scale where the abundance of H is 12) to 7.50, in agreement with the meteoritic value. This last modification stemmed from improvements in atomic data used to analyze solar spectrum (e.g., Holweger et al., 1991; Biémont et al., 1991), and is largely supported by more modern analyzes (Asplund et al., 2000a,b; Asplund, 2000; Bellot Rubio and Borrero, 2002).

The next major revision came to the photospheric abundance of O by Allende Prieto et al. (2001), who applied a three-dimensional time-dependent hydrodynamical model solar atmosphere to the observed 6300 Å line. These authors recognized that this line, attributed to a forbidden line of neutral O, is also blended with Ni I, with the result that the O abundance of 8.83 in Grevesse and Sauval (1998) (8.93 in Anders and Grevesse, 1989) was revised down to 8.69 ± 0.05. A number of subsequent papers analyzing other allowed and forbidden lines in O I, and also molecular OH supported this change (Asplund et al., 2004, 2005c; Meléndez, 2004; Socas-Navarro and Norton, 2007; Meléndez and Asplund, 2008), though Ayres (2008) and Caffau et al. (2008) offered more cautious views. Joining, O, C (Allende Prieto et al., 2002; Asplund et al., 2005b; Caffau et al., 2010) and N (Caffau et al., 2009) also underwent downward revisions in their abundances.

In Table 1, we collect the recommended solar photospheric abundances of various commonly observed elements from Grevesse and Sauval (1998), Asplund et al. (2009) [also given in Grevesse et al. (2010)], Caffau et al. (2011), and Scott et al. (2015a,b) and Grevesse et al. (2015) for comparison and reference. Not given here are result from Lodders (2010), who for the elements of most interest here appears to quote the average of Asplund et al. (2009) and Caffau et al. (2011). The data sources for each element are all listed in these reviews. For future reference we remark that aside from the revisions above, the noble gases will be of interest to us, since their photospheric abundances are often determined from coronal observations (e.g., Feldman and Widing, 1990; Young, 2005a), on the assumption that no fractionation occurs between the photosphere and the corona for these elements. This is an assumption we shall scrutinize. Only He is determined independently, from helioseismology (Basu and Antia, 2004), in an analysis that includes the revised solar metallicity.

Table 1: Recommended Solar Photospheric Abundances of Common Elements

2.2 Helioseismology

The re-evaluation of the solar composition above has revised the solar metallicity down from 0.0170 (Grevesse and Sauval, 1998) to the range 0.0153 (Caffau et al., 2011) to 0.0134 (Asplund et al., 2009), with Asplund et al. (2005a) giving a value as low as 0.0122, largely driven by improved analysis of lines of C, N, and O. The lower metallicity decreases the sound speed at the base of the solar convection zone, yielding now a larger disagreement between observed and modeled sound speeds (see, e.g., Figure 1 in Guzik and Mussack, 2010). The reduced abundances also decrease the depth of the convection zone in solar models, again worsening agreement between models and helioseismic inversions (e.g., Basu and Antia, 2004).

Figure 1:

Full-disk solar emission measure distribution, with low FIP elements depicted by solid symbols, high FIP elements by open symbols. The transition from photospheric abundances at log T < 6.0 to coronal abundances at higher temperatures, indicating that different types of coronal structures are emitting above and below this temperature. Image reproduced with permission from Laming et al. (1995), copyright by AAS.

One early solution proposed was to increase the abundance of Ne to compensate (Antia and Basu, 2005; Bahcall et al., 2005a), by bringing the solar metallicity back to its prior value. A survey in nearby active stars had previously yielded the abundance ratio Ne/O in the range 0.3–0.4 (Drake and Testa, 2005), significantly higher than the solar coronal value and closer to that suggested. Drake and Testa (2005) argue that the relative constancy of this ratio in a sample of over 20 stars suggests that the “true” Ne/O abundance ratio should be around 0.4, and that the variation in the solar corona must be due to some unknown fractionation. More recent work suggests than an increased Ne abundance (of about 0.5–0.67 dex) is not a complete fix (Lin et al., 2007), but a more modest increase of 0.45 dex is still acceptable (see introduction of Guzik and Mussack, 2010). Ne, and also possibly Ar, are the focus of revisions to composition because having no photospheric absorption lines, their abundances can only be measured in the solar corona, or in astrophysical sources as proxies for the solar photosphere. Asplund et al. (2009) argue for an Ne/O abundance ratio of 0.175 ± 0.031 following the measurements of Young (2005a) in the solar corona. Other authors have suggested that increased opacity (Christensen-Dalsgaard et al., 2009; Serenelli et al., 2009), beyond that implied by the increase due to data from the Opacity Project replacing older OPAL radiative opacities (Bahcall et al., 2005b) might ease the problem, while variations to the solar evolutionary history with extra episodes of mass loss of accretion have also been considered (Guzik and Mussack, 2010; Serenelli et al., 2011). Villante et al. (2014) provide a recent evaluation, accounting for helioseismic and solar neutrino data, again favouring the older photospheric abundance set of Grevesse and Sauval (1998). Even more recently, Shearer et al. (2014) study the variation of Ne/O measured by Ulysses/SWICS and ACE/SWICS over the solar cycle between 1998 and 2012. Their results also favour a low Ne/O abundance ratio in the range 0.10–0.15, although with unexpected variation.

Bergemann and Serenelli (2014) review these and other potential solutions to the “solar abundance problem”. Other ideas include that of Lopes and Silk (2013), who revisit the helioseismology problem in the light of revised photospheric abundance for the Sun and solar-like stars. Relative to solar analogs without planetary systems, the Sun appears to be underabundant in metals, more so in refractory elements than in volatiles. The mass of the “missing” elements from the solar convection zone appears to be similar to the combined mass of the inner terrestrial planets, Mercury, Venus, Earth and Mars, leaving open the possibility that the metallicity of the solar interior, specifically the radiation zone, is higher than that of the convection zone, as appears to be required. Lopes and Silk (2013) explore several such models, computing the solar neutrino spectra with a view to future observational capabilities. Their models however appear to need high mass loss from the young Sun, which might be problematic (cf. Wood, 2004, 2006). Zhang (2014) considers the effect of a turbulent kinetic flux within the solar convection zone. A negative flux, i.e., turbulence propagating from the convection zone to the radiation zone, goes some way to restoring agreement. A downwards turbulent kinetic flux requires larger outward radiative and convective energy fluxes, which lead to a deeper boundary between the convection and radiation zones.

Finally, the solar helium abundance is most accurately determined from helioseismology, from the anomaly produced in the sound speed at the depths in the convection zone where helium ionizes. Villante et al. (2014) give the value as Y = 0.2485 ± 0.0035, apparently the mean of the results derived by Basu and Antia (2004) using GONG or MDI data.

3 The Solar FIP Effect: Overview

As mentioned above, the observation of element abundances in the solar corona and wind has a history spanning decades, and has been reviewed several times during that period (Meyer, 1985a,b; Feldman, 1992; Feldman and Laming, 2000; Feldman and Widing, 2002, 2003, 2007). Here, rather than provide an exhaustive review, we attempt to summarize and update the status of solar coronal abundances, and refer readers back to these reviews for extensive references.

In contrast to photospheric abundances which are generally measured and given relative to H (i.e., absolute abundances), with a few exceptions to be noted below, most coronal abundance measurements and results are relative, in that one minor ion is compared to another minor ion (often O) with no reference to H. This arises due to the difficulties in observing H. H generally has no observable emission lines from the solar corona in bandpasses in which other elements are observed, and requires different in situ instruments for detection to those for heavy ions. Both difficulties lead to cross calibration issues. Exceptions occur in the UV where H emission lines can sometimes be detected, or in the X-ray region where the thermal bremsstrahlung continuum can be taken as an indicator of the H abundance. We will highlight these features where appropriate below.

Theoretically, it will also turn out to be easier to discuss relative abundances. Modeling the action of the ponderomotive force on minor ions in an ambient H atmosphere is much more straightforward than the multifluid calculation that would be necessary to treat the back reaction of the Alfvén waves on the H fluid itself, and to incorporate those effects into the predicted FIP fractionations. In fact in many cases, it turns out the H and O behave similarly because of their strong charge exchange coupling, due to their similar ionization potentials, and this provides some justification for our approach.

In the quiet solar corona and slow speed solar wind, elements with first ionization potential (FIP) below about 10 eV are enhanced in abundance by a factor of about 3, with typical variations in the range 2–5. This is established by both remotely sensed (i.e., spectroscopic) and in situ measurements and at the time of writing, despite early controversy, is now considered an established fact. Variations in the fractionation with solar region exist. Coronal holes, and the fast solar wind emanating from them are known to have a significantly smaller degree of FIP fractionation than the quiet corona and slow wind (e.g., Bochsler, 2007a; Feldman, 1998b). Brooks and Warren (2011) show that FIP fractionated abundances measured in an active region with the Extreme Ultraviolet Imaging Spectrograph (EIS) on Hinode (Culhane et al., 2007) match those detected a few days later when the solar wind from this active region would have reached 1 AU. The Sun viewed “ as a star” (Laming et al., 1995) shows FIP effect only for temperatures above about 10⁶ K. This is illustrated in Figure 1, taken from Laming et al. (1995), where the full-disk solar emission distribution is determined from the solar spectrum of Malinovsky and Heroux (1973), based on emission lines from low FIP (filled symbols) and high FIP (open symbols) elements. The two emission measures coincide up to log T ≃ 6, and thereafter diverge, indicating overabundance of low FIP elements. This result is corroborated by Young (2005b,c), Feldman and Widing (1993); Feldman (1998a), and Young and Mason (1998), and leads to the conclusion that structures emitting at temperature below 10⁶ K must be distinct entities from those responsible for the higher temperature emission. Feldman and Laming (1994) elaborate this argument based on earlier observations, most notably those in Feldman (1983, 1987). It appears likely that the high temperature FIP fractionated plasma resides in coronal loops fed by chromospheric evaporation (the response of chromospheric plasma to heat released in the corona conducted downwards, see e.g., Bray et al., 1991; Reale, 2014), while the lower temperate plasma, attributed to “unresolved fine structures” by Feldman (1983, 1987), can now be identified with the recently discovered Type II spicules (De Pontieu et al., 2011; Martínez-Sykora et al., 2011), or other dynamic loop structures (Hansteen et al., 2014) recently observed with the Interface Region Imaging Spectrograph (IRIS). Individual features distinct from Type II spicules at transition region temperatures (10⁴ K < T < 10⁶ K) may show FIP fractionation (for examples see Feldman, 1992; Feldman and Laming, 2000; Feldman and Widing, 2002, 2003, 2007). We emphasize again that the result of Laming et al. (1995) applies to the “Sun as a star”.

Active regions and flares can also have different fractionation, often reduced from that observed in the quiet Sun. This is most clearly seen in spectra acquired of plasma above a sunspot (Feldman and Widing, 1990). Phillips et al. (1994) also measured a maximum Fe enhancement of a factor of 2 between photosphere and corona, by comparing the photospheric Fe Kβ line excited by flourescence with the collisionally excited coronal Fe xxv resonance line observed during flares by the YOHKOH Bragg Crystal Spectrometer (Culhane et al., 1991). Later work with RHESSI (Lin et al., 2004) found much stronger enhancements in the abundance of Fe relative to H from line to continuum measurements (Phillips et al., 2006). Abundances of other elements in flares relative to H have been measured by RESIK (Sylwester et al., 2005). FIP fractionations for K, Ar, Cl, S, Si and Al have been given by Sylwester et al. (2008), with more detailed results given in subsequent papers (Sylwester et al., 2010a,b, 2011, 2012, 2013, 2014), and given in more detail in Table 3 for comparison with model results. Warren (2014) finds almost no FIP fractionation in 21 flares observed with the EUV variability Experiment (EVE) on the Solar Dynamics Observatory (SDO), similar to Fludra and Schmelz (1999), while Del Zanna and Mason (2014) find a typical enhancement in the abundance of Fe compared to O and Ne of 3.2 in 9 flares observed by the Flat Crystal Spectrometer (FCS) on the Solar Maximum Mission (SMM). Brooks and Warren (2012) and Widing and Feldman (2008) find similar enhancements.

Coronal mass ejections (CMEs) observed in situ often have strong FIP fractionation as shown in a survey (Reisenfeld et al., 2007) conducted with data the Advanced Composition Explorer (ACE Gloeckler et al., 1998) and the Genesis mission (Burnett et al., 2003). Zurbuchen et al. (2004) and Smith et al. (2001) show that frequently these large FIP fractionations are associated with the CME flux rope, possibly implying that the flux rope forms in the corona and does not emerge preformed from the photosphere (in which case it might be expected to exhibit photospheric abundances). CMEs can also exhibit mass dependent fractionation (Wurz et al., 2000), most likely indicating the role of processes other than FIP fractionation in modifying the elemental composition of the solar upper atmosphere.

We have already mentioned the difference in FIP effect between fast and slow speed streams observed by Ulysses (Zurbuchen et al., 1999; von Steiger et al., 2000). Lepri et al. (2013) study the evolution of abundances of fast and slow solar wind observed in the ecliptic by the Advanced Composition Explorer (ACE). While other solar wind parameters such as charge states, magnetic fields and freeze-in temperatures show marked variation, the degree of FIP fractionation (i.e., element abundances relative to O) does not. Absolute abundances, measured relative to H, do show some variation, with the lowest abundances of He, C, O, Si and Fe being observed in the slowest wind at solar minimum. Interestingly, their absolute abundances for O support the revised photospheric abundance of O (Asplund et al., 2009), with the highest mean O/H abundance ratio in the slow speed wind at solar maximum being 8.68 (in logarithmic notation), with upper and lower limits of 8.42 and 8.94 respectively, from their Table 1. Previous studies of this sort (Bochsler, 2007b; von Steiger et al., 2010) have favoured the “older” O abundance (8.83 Grevesse and Sauval, 1998). von Steiger et al. (2010) assume that the high speed solar wind gives the most faithful representation of photospheric abundances (their O/H value in slow speed solar wind agrees with Asplund et al., 2009). Bochsler (2007b) plots O/H against He/H in his Figure 3. and shows a striking correlation between them, arguing that inefficient Coulomb drag is the cause of both variations. This might appear to be problematic, in that O is not always depleted relative to H (unless one takes oldest O/H value from Anders and Grevesse, 1989, as the correct value), but He is, with the problem becoming worse for the more recent O/H values.

The solar slow speed wind helium abundance has long been known to be depleted from the photospheric value, and this depletion is now established to vary with solar slow wind speed and the phase of the solar activity cycle (Aellig et al., 2001; Kasper et al., 2007) in a similar manner to that mentioned above (Lepri et al., 2013). Figure 2 (left panel, from Kasper et al., 2012) shows the He/H abundance ratio measured by the Wind spacecraft over 1.5 solar cycles, in bins of different solar wind speed. Greater variability is seen in the slowest wind speed bins, and in the slowest bin, the variability matches the smoothed sunspot number. The right panel of Figure 2 show a similar study with ACE by Rakowski and Laming (2012), where the abundance ratio He/O is plotted. Broadly similar behavior with solar wind speed is seen, but the solar cycle dependence is less pronounced, but still apparent. The fast solar wind helium abundance is also depleted, but to a lesser degree than the slow wind, and is also less variable. Measurements of the helium abundance in coronal holes (Laming and Feldman, 2003) and in the quiet solar corona (Laming and Feldman, 2001) generally show similar values to those measured in the solar wind, indicating that the helium depletion occurs lower down in the solar atmosphere than the corona. A spectroscopic measurement in a solar flare (Feldman et al., 2005) showed a much higher abundance of helium, in qualitative agreement with the by now routine observation in situ of enhanced (i.e., less depleted) helium abundance in CMEs (e.g., Wimmer-Schweingruber et al., 2006).

Figure 2:

Left: Helium abundance relative to hydrogen in the slow speed solar wind over 1.5 solar cycles. The curve colors denoted the wind speed at which at abundance is measured. He is more variable in the slowest slow speed solar wind. The black curve gives the monthly smoothed sunspot number. Right: Helium abundance relative to oxygen in the slow speed solar wind, measured by ACE/SWICS. The same trend of depletion with wind speed as for He/H is seen, but the solar cycle dependence is less pronounced. Images reproduced with permission from [left] Kasper et al. (2012) and [right] Rakowski and Laming (2012), copyright by AAS.

Widing and Feldman (2001) studied the variation of the FIP effect with time in newly emerged active regions. They found that the new loops emerged with photospheric abundances, and gradually changed to coronal abundances, i.e., developed a FIP effect, over the course of a few days. Consequently a new active region should have a weak FIP effect, while an older one would show strong fractionation. Recent observations by Baker et al. (2013) corroborate this view. Figure 3 shows maps of intensity, non-thermal velocity, photospheric magnetic field and coronal FIP bias derived for a sigmoidal anemone active region observed by EIS/Hinode. The overlaid black ellipses show the footpoints of loops, coincident with strong photospheric magnetic field concentrations, while the dotted black lines show the loop connections between them. The strongest FIP effect can be seen at the loop footpoints, also coincident with strong nonthermal velocities. Weaker FIP effect is seen along the loop connections, suggesting that the FIP effect originates in the chromosphere, and is communicated to the coronal loop by transport processes. The active region seen here would then be considered relatively new, since only weak FIP effect is seen in its coronal connections.

Figure 3:

Maps of intensity, non-thermal velocity, photospheric magnetic field and coronal FIP bias derived for a sigmoidal anemone active region observed by EIS/Hinode. The overlaid black ellipses show the footpoints of loops, coincident with strong photospheric magnetic field concentrations, while the dotted black lines show the loop connections between them. The strongest FIP effect can be seen at the loop footpoints, also coincident with strong nonthermal velocities. Image reproduced with permission from Baker et al. (2013), copyright by AAS.

4 Stellar FIP and Inverse FIP Effects

The measurement of element abundances in stellar coronae became possible for the first time with the 1992 June 7 launch of the Extreme Ultraviolet Explorer (EUVE) satellite. The use of grazing incidence gratings allowed strong lines in the EUV spectra of stars to be resolved, allowing the acquisition of data on stellar corona of similar quality to the early solar spectra analyzed by e.g., Pottasch (1963). The Advanced Satellite for Cosmology and Astrophysics (ASCA) launched on 1993 February 20 provided X-ray spectroscopy of stellar coronae with CCD-level spectral resolution. Individual lines could not be resolved, but the He- and H-like line complexes of different elements could. Other missions from which a few results emerged were Ginga (launched on 1987 February 5), ROSAT (launched 1990 June 1) and BeppoSAX (launched 1996 April 30) which carried proportional counters for spectroscopy (gas scintillation proportional counters in the cases of Ginga and BeppoSAX) which allowed measurements of the He-like Fe complex of lines with respect to the surrounding continuum. More recently, Suzaku (launch 2005 July 10) has also provided CCD X-ray spectra, although the higher resolution calorimeter failed soon after launch.

The review of Feldman and Laming (2000) covered the status of this new field at a time when the results from EUVE and ASCA were available, but before the launches of Chandra and XMM-Newton (launched 1999 July 23 and 1999 December 10, respectively). These satellites both carry grating instruments as well as CCD cameras, and so high spectral resolution X-ray spectra of stellar coronae are acquired with significantly higher throughput than was the case with EUVE or ASCA. Testa (2010) provided a more updated view of the field, encompassing a wider variety of stellar targets. Here, we will recap the discussion of Feldman and Laming (2000), and the later reviews of Favata and Micela (2003), Drake (2003) and Testa (2010), concentrating on stars of varying spectral type but in other respects similar to the Sun, with a view to the theoretical discussions to follow in Sections 6 and 7.

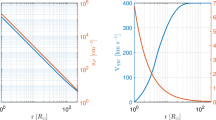
Wood and Linsky (2010) conducted a survey of stellar FIP effects restricted to stars with X-ray luminosities less than 10²⁹ erg s⁻¹, with results shown in Figure 4 (adapted from Figure 9 of their paper, also including points for α Cen B, π³ Ori and GJ338). By excluding the most active stars, a clear trend of decreasing stellar FIP effect with later spectral type is uncovered. The Sun is at the bottom left of Figure 4, with a logarithmic FIP bias −0.6 (expressed as log (X/H)_phot — log (X/H)_cor, so that this is a coronal low FIP enhancement of 10^0.6 ≃ 4), along with other stars of similar spectral type (π¹ UMa (G1V) and χ¹ Ori (G0V); Güdel et al., 2002). The degree of fractionation diminishes as one moves to later spectral type, becoming zero at about K5, and an inverse FIP effect is observed in the M stars. The magnetic fields of a sunspot umbra and penumbra are likely to be similar to those found more ubiquitously in the atmospheres of later type (i.e., M) stars (see Donati and Landstreet, 2009), so the results of Feldman and Widing (1990) and Phillips et al. (1994) appear consistent with these stellar results. At the extreme left hand side, the result for χ³ Ori suggests that the FIP effect saturates at a value similar to that found in the Sun, a low FIP enhancement of about 4, and does not continue increasing at spectral types earlier than this. The properties of the various stars are summarized in Table 2. Wood et al. (2012) show that the sample of T Tauri stars from Güdel et al. (2007) show a similar trend of Ne/Fe as in Figure 4, but generally at higher FIP bias (i.e., stronger Inverse FIP effect). Other more active stars (X-ray luminosities larger than 10²⁹ erg s⁻¹) also show generally larger inverse FIP than those in Figure 4. We do not consider these further because of complications to the stellar physics introduced by fast rotation and tidal interactions in close binaries that are typical of these types of stars.

Figure 4:

Survey of FIP fractionation (log (X/H)_phot − log(X/H)_cor) observed in a sample of dwarf stars, updated from Wood and Linsky (2010), where values below zero indicate a solar-like FIP effect and values above zero indicate an inverse FIP effect. Points for GJ338 and π³ Ori have been added from Wood et al. (2012) and Wood and Laming (2013), respectively, and αCen B from Drake et al. (1997). Diamonds indicate measurements from Telleschi et al. (2005), triangles from Liefke et al. (2008), with a solar value from Feldman and Laming (2000). For all GK stars, the FIP bias calculations include corrections for stellar photospheric abundances from Allende Prieto et al. (2004), but for the M stars there are in general no stellar photospheric measurements available so we have to simply assume solar photospheric abundance apply. Among these, EV Lac is the strongest case, due to chromospheric evaporation of photospheric abundance material observed during flares (Laming and Hwang, 2009, and references therein). For the purposes of this figure, we avoid extremes of stellar activity, confining our attention to stars with log L _X ≤ 29. Reproduced by permission of the AAS.

Table 2: List of FIP Bias Assessments for Main-Sequence Stars. Table updated with permission from Wood et al. (2012), copyright by AAS.

Anticipating a connection between the coronal abundance anomalies, and the chromospheric wave field, arising either from waves produced in the corona and propagating down, or as a result of helioseismic or asteroseismic p-modes, we make the following comments about some of the important stars in Figure 4.

α Cen AB: This inactive G2 V+K1 V binary is not in the original sample of Wood and Linsky (2010), but it is of prime interest since its fundamental parameters (photospheric abundances, p-mode frequencies, mass, radius, surface gravity, and effective temperatures) are very well known for both stars (e.g., Bedding et al., 2004; Butler et al., 2004; Kjeldsen et al., 2005; Porto de Mello et al., 2008; Bruntt et al., 2010; Karoff et al., 2007; Chaplin et al., 2009). Coronal abundances were first measured by Drake et al. (1997) from EUVE data, yielding a FIP effect of about a factor of two in the unresolved binary. Subsequent observations determined that α Cen B is the dominant coronal source, which places it in its spot in Figure 4. There are many observations by both XMM and Chandra (e.g., Raassen et al., 2003b; Liefke and Schmitt, 2006), and model chromospheres of both stars have been developed (Ayres et al., 1976; Jordan et al., 1987; Vieytes et al., 2009). Fe XII 1242 Å linewidths are available in Ayres et al. (2003).

ε Eri: Laming et al. (1996) first measured coronal abundances for this moderately active K2 V star with EUVE. More recent spectra from XMM and Chandra have been extensively analyzed as well (Sanz-Forcada et al., 2004; Wood and Linsky, 2006; Ness and Jordan, 2008). Drake and Smith (1993) give fundamental parameters (see also Table 2 in Vieytes et al., 2009). Only theoretical estimates of ε Eri’s p-mode spectra are available (Gai et al., 2008). Several sources provide model chromospheres (Jordan et al., 1987; Sim and Jordan, 2005; Vieytes et al., 2009). Ayres et al. (2003) give the Fe xII 1242 Å width from which coronal turbulence may be deduced.

ξ Boo A: This is a G8 V dwarf with coronal abundances first measured with EUVE by Laming and Drake (1999) and Drake and Kashyap (2001), and later with Chandra (Wood and Linsky, 2010). Model chromospheres are available from Kelch et al. (1979) and Jordan et al. (1987).

70 Oph A: This K0 V dwarf with an X-ray spectrum was analyzed by Wood and Linsky (2010). Its fundamental parameters are given by Bruntt et al. (2010), including p-mode oscillation frequencies (Carrier and Eggenberger, 2006; Eggenberger et al., 2008). No empirical model chromosphere is available for this star, but there is a theoretical one from Schmitz and Ulmschneider (1980). Further guidance may come from the K dwarf model chromospheres of Vieytes et al. (2009). It is also included in the survey of forbidden line observations by Ayres et al. (2003).

M dwarfs: The cluster of M dwarfs at top right in Figure 1 are studied by Liefke et al. (2008). A model chromosphere for AD Leo is given by Fuhrmeister et al. (2005), and a grid of model chromospheres for M1 dwarfs is given by Houdebine and Stempels (1997). Ayres et al. (2003) give linewidths for the Fe XII 1242 A and Fe XXI 1354 Å forbidden lines. EV Lac is most recently studied by Laming and Hwang (2009) using Suzaku observations before and during a flare. It exhibits abundance change during flares; the inverse FIP quiescent corona giving way to a more “normal” (i.e., solar photospheric) abundance pattern. This is interpreted as evidence of chromospheric evaporation, where unfractionated plasma is evaporated up into a flaring loop, lending more confidence to the inverse FIP interpretation.

Favata and Micela (2003) and Sanz-Forcada et al. (2004) caution that for several stars with apparent metal depletion in their coronae, determined from the Fe/H ratio, the coronal abundances merely reflect metal-poor photospheres. In Figure 4, AD Leo maybe such a case (Jones et al., 1996), although it clearly shows a nonsolar Ne/Fe abundance ratio. However, metal-depleted coronae or inverse FIP effect, do appear to clearly exist in some cases, e.g., II Peg (K2 IV plus an unseen companion; Huenemoerder et al., 2001), AR Lac (G and K subgiants in a 1.98 day orbit; Huenemoerder et al., 2003) and AB Dor (K2 IV–V with a 0.515 day spin period; Sanz-Forcada et al., 2003). Further, the variation of element abundance during stellar flares, in which initially metal depleted plasma evolves towards the standard composition, interpreted in terms of the chromospheric evaporation of unfractionated plasma to the coronal flare site, seems to require the existence of such abundance anomalies. Such phenomena are observed in HR 1099 (K1 IV and G5 IV; Audard et al., 2001), Algol (B8 V and K2 IV; Favata and Schmitt, 1999), and UX Ari (G5 V and K0 IV; Güdel et al., 1999) where the later type subgiant is taken to be the main source of coronal emission, as well as AB Dor (Güdel et al., 2001b), YY Gem (dMe and dMe with 0.814 day orbit; Güdel et al., 2001a), II Peg (Mewe et al., 1997), AT Mic (dM4.5 and dM4.5; Raassen et al., 2003a), and EV Lac (dMe3.5e; Laming and Hwang, 2009). Many of these more active stars show stronger Inverse FIP effects than shown in Figure 4.

Not included in Figure 4, but also of interest for having neither a solar-like FIP effect nor an inverse FIP effect is Procyon. Coronal abundances measured with EUVE, Chandra and XMM (Drake et al., 1995b,a; Raassen et al., 2002; Sanz-Forcada et al., 2004). At spectral type F5 does not follow the trend of Figure 1 (it is, however, a subgiant, not a solar-like dwarf star). Extensive asteroseismological observations are available for Procyon (e.g., Mosser et al., 2008; Leccia et al., 2007). In fact, its p-mode lifetimes are known to be significantly shorter than those of the Sun (Bedding et al., 2010). Chromospheric models are available for us to use for this well-studied star (Ayres et al., 1974; Evans et al., 1975; Brown and Jordan, 1981).

Another interesting case is τ Bootis (Maggio et al., 2011). It is a F7 V dwarf, with a M2 V companion. Following the assumption of Maggio et al. (2011) that the F7 V star is responsible for the X-ray emission, it is also discrepant from the trend in Figure 4, with F_bias = −0.17 at spectral type F7. τ Bootis A has already attracted interest because it hosts a close-in giant planet (τ Boo b: P_rot = 3.31 days, M sin i = 3.9M _J ) Butler et al., 1997). A star-planet interaction has been noted, in that the planet appears to be inducing an active region on the star, that leads the planet by ∼ 70° in longitude (Shkolnik et al., 2008; Walker et al., 2008), and this opens the possibility of the planet also affecting the coronal abundances, due to waves induced in the stellar atmosphere. Another possibility of course is that the XMM observation is contaminated by emission from the M2 companion. Another curiosity is that the photospheric abundances of τ Boo A do not agree with the trend reported by Lopes and Silk (2013), being of order 0.2 dex higher than solar values (Maggio et al., 2011). ε Eridani also hosts a Jupiter mass planet, but shows no coronal abundance discrepancy from the trend in Figure 4.

5 Early Theoretical Models: Overview

5.1 Diffusion models and variations

The earliest attempts to explain that FIP effect invoked various processes like thermal and ambipolar diffusion (in a stationary atmosphere) or inefficient Coulomb drag (in a moving case). Thermal diffusion arises in a temperature gradient, with minor ions diffusing towards higher temperatures. This happens because collision cross sections decrease with increasing collision energy, and so the force from the hotter particles from the direction in which the temperature is rising is lower than than from the colder direction. This obviously will select ions over neutrals, and accelerate them towards the corona. However, such a process is inherently slow (Hénoux, 1995, 1998), and requires static conditions for periods ranging from tens of hours (Hansteen et al., 1994) to days or weeks (Killie and Lie-Svendsen, 2007). This appears increasingly at odds with the modern view of the solar chromosphere as a dynamic environment, continually being perturbed by the passage of shocks (Carlsson and Stein, 2002) or reconnection at chromospheric layers (Isobe et al., 2008). It also conflicts with the argument that in the absence of mass supply from below, the solar wind would empty the corona within 1–2 days. Clearly, any fractionation mechanism that takes longer than this to change coronal abundances cannot be right. Ambipolar diffusion refers to the diffusion of neutrals along an ionization balance gradient, and must also be considered in such models, though by itself does not appear capable of causing FIP fractionation. Hansteen et al. (1997) also demonstrate that chromospheric mixing, in their case between hydrogen and helium, is also necessary to prevent gravitational settling of helium in the chromosphere and to give a realistic abundance of helium in the solar wind.

In an attempt to speed up the fractionation process by thermal means, various authors have modeled the separation of elements entrained in a flow of neutral hydrogen and protons. von Steiger and Geiss (1989) considered such a flow driven across magnetic field lines, either a horizontal flow across vertical field lines, where gravity plays no role in the fractionation, or a vertical flow driven across horizontal field lines, where it does. FIP fractionations matching observations reasonably well are achieved, but the models themselves must be considered highly idealized and unlikely to represent the real sun. No mechanism is suggested to produce such a cross-field flow. In a treatment of fractionation in a (more plausible) vertical flow along vertical field lines, Marsch et al. (1995) solve diffusion equations for ions and neutrals separately in the background flow. These equations only include photoionization of neutrals. No recombination of ions and electrons is accounted for [their Eqs. (6) and (9)]. At the lower boundary the gas is assumed completely neutral, with density n (s = 0) = n₀. The neutral density gradient is specified at the upper boundary, taken to be where the gas is completely ionized, and is accelerated into the solar wind. Here, dn/ds (s = S) = 0 and the ion density also n⁺ (s = S) = 0. Finally, the ion density gradient at the lower boundary dn⁺/ds (s = 0) = 0. The boundary conditions on n and n⁺ are justifiable, and do not greatly affect the solutions. Different choices can lead to the same diffusive fluxes. The choices of boundary conditions for the density gradients are less clear, and these are crucial to obtaining FIP fractionation in the model. In fact, it is precisely the choice of dn⁺/ds (s = 0) = 0 that specifies the ion flux at the upper boundary, with value ${n_0}\sqrt {D/\tau}$, where $D = {v_j}^2/{\nu_{jH}}$, the diffusion coefficient for neutrals of element j in background of neutral H, in terms of its thermal speed and collision frequency with H, and τ is photoionization time for neutral j in the chromospheric radiation field. The fact that the ion flux at the top of the chromosphere depends ultimately on the characteristics of neutrals at the bottom through the diffusion equation, and especially so for the FIP fractionated low FIP elements that in reality have very small neutral fractions throughout the region of interest, is indicative of problems. McKenzie et al. (1998) and McKenzie (2000) point out that in a gas where collisions play the dominant role in coupling species together, FIP fractionation cannot occur in a one dimensional steady state model. If all elements enter at the lower boundary with the speed of H, and leave at the upper boundary with at the proton speed, continuity demands that no fractionation occur. They also conclude that the boundary condition on the density gradient at the lower boundary is the cause of the fractionation in this model, and that such fractionation must have taken place below the lower boundary. Indeed, Eq. (71) of Marsch et al. (1995) giving the upper boundary condition on the exiting ion fluxes suggests that the FIP fractionation is already embodied in the inputs to the model, rendering the model explanation spurious.

Fractionation in such a class of models is not completely ruled out. If the chromosphere can respond to the enhanced coupling of ions to protons in the upper chromosphere (compared to that of neutrals) by allowing diffusion to supply ions from below at a greater rate, i.e., dn/ds has to vary with species. But this reliance on diffusion places a limit on the speed with which abundance modification may take place. There are some newer models (Pucci et al., 2010) investigating the changes in abundances with hydrogen flux through a chromospheric magnetic funnel, but this requires significant fine tuning for each element (Pucci et al., 2010, consider O, Ne, and Fe), and appears unlikely to be able to get every element right at the same time, even if the atmosphere was sufficiently quiescent (see also Byhring et al., 2011; Byhring, 2011). Bø et al. (2013) make the point that above the chromospheric temperature minimum, the atmosphere is convectively stable, but ignore the fact that waves from the convectively unstable regions may continue to propagate upwards to perturb higher altitudes, as in e.g., Heggland et al. (2011). They consider the effect of gravitational settling within the chromosphere as a means of fractionation among O, Ne, S, and Fe. The mechanism only appears capable of producing a depletion of high FIP elements (no enhancement of low FIPs as observed), and then only with a static atmosphere. An episodic upflow to supply the corona, punctuated by periods of stasis to allow the fractionation to occur. Both Pucci et al. (2010) and Bø et al. (2013) use somewhat unrealistic chromospheric models, in that the degree of hydrogen ionization for a given density is lower than that in Avrett and Loeser (2008), at least for the models which come closest to matching observed abundance anomalies. Although the Avrett and Loeser (2008) model is quasi-static designed to match spectroscopic observations, it matches quite well with average chromospheric structures modeled in Heggland et al. (2011), as does its antecedent (Vernazza et al., 1981, VALC) compared with Carlsson and Stein (2002), at least in terms of electron density.

The helium depletion explained by such processes (Byhring, 2011) is also at odds with the observation that it (and the other minor ions) flow faster than hydrogen in the solar wind at 1 AU (Neugebauer et al., 1996; Kasper et al., 2008; Bourouaine et al., 2011). A further stage of solar wind acceleration must set in at a level above that where the He depletion sets in (Wang, 2008). Noci et al. (1997), following Geiss et al. (1970), make the point that if such processes were the origin of the solar wind He abundance depletion, other heavy ions should also be depleted, which is now known not to be the case. Bochsler (2007b) revisits this, comparing He, O, and Ne for which He appears most affected by gravitational settling, or inefficient Coulomb drag, in the corona. In this case the He abundance should correlate with the proton flux, which is not observed (Wang, 2008). However, all these elements appear also to vary with respect to H, leaving open the possibility that quasi-thermal or diffusive processes play some role in establishing the absolute coronal abundances.

5.2 Thermoelectric driving

Perhaps the best early model was that of Antiochos (1994). Cross B diffusion of chromospheric ions into a flux tube by a thermoelectric force associated with downward heat conducting electrons from a closed loop enhances the loop footpoint abundances of ions, but not neutrals. Given ∇ × E = 0 in steady state conditions, the transverse gradient of the longitudinal electric field (due to the plasma resistivity) must be balanced by a longitudinal gradient of the transverse electric field. This transverse electric field points into the flux tube, thus concentrating ions therein. The predicted fractionation pattern is proportional to ion mass^1/2 (it is independent of mass for the ponderomotive force). In a sense, this is conceptually very similar to the ponderomotive force model, in that it is the loop’s response to coronal heating that causes the fractionation, except here it is mediated by heat conduction rather than Alfvén waves. The main problem is that heat must be conducted down to regions of the chromosphere without transverse magnetic structuring (there must be plasma surrounding the flux tube), and this appears unlikely. It is unclear where in the chromosphere horizontal structuring sets in, but a natural place to expect it is likely to be the equipartition layer, where the Alfvén speed and sound speed are equal, roughly where the plasma β ≃ 1. The stopping distance of 1 keV electrons is of order 1 km at a density of 10¹² cm⁻³, so downwards heat conduction is unlikely to reach this far, and other authors have recently considered energy transport by Alfvén waves (Fletcher and Hudson, 2008; Haerendel, 2009). Alfvén waves may still fractionate material in the upper magnetically structured layers of the chromosphere, because ions move vertically along the flux tube rather than horizontally across it. Antiochos (1994) also does not allow for an “Inverse FIP Effect”. Laming and Hwang (2009) discuss how the ponderomotive force may also inhibit downwards heat conduction, but large Alfvén wave amplitudes are required.

5.3 Chromospheric reconnection

Arge and Mullan (1998) consider chromospheric reconnection giving ions a larger density scale height than neutrals. They model this using the Zeus code, iterating between its hydrodynamic and magnetohydrodynamic implementations to treat the neutrals and ions respectively, with these two fluids being coupled by collisions. They only calculate Si and Ne as examples, so it is not possible to evaluate the full fractionation pattern such a process would produce. The ion-neutral coupling rate they use appears to be that due to charge exchange collisions between protons and neutral hydrogen [their Eq. (6)], and this appears to be applied to all elements, with possible modifications to the collision velocities. This is not correct, and the coupling should more properly be described by elastic scattering (cf. Malyshkin and Zweibel, 2011). In fact, looking at these ion-neutral collision rates a mass dependent fractionation appears likely, not the FIP effect, which might be relevant to the observations of Wurz et al. (2000).¹ By contrast Laming (2004a) and Laming (2012) devoted considerable effort to the correct description of these atomic processes. Arge and Mullan (1998) also predict FIP effect everywhere, with no difference between coronal holes and closed loops, unless extra assumptions are made about the presence or absence of chromospheric reconnection in open and closed field, and cannot reproduce an “Inverse FIP Effect”.

5.4 Ion cyclotron wave heating

Schwadron et al. (1999) offered the first mechanism of fractionation by wave-particle interactions. Coronal ion cyclotron (IC) waves propagate down and heat chromospheric ions, not neutrals. The FIP effect arises from the preferential heating combined with the coupling of the chromospheric minor ions to a background flow of H atoms and protons. The formalism for this coupling is elegant, and forms the basis for models invoking the ponderomotive force to be discussed at greater length elsewhere in this paper.

The fractionation pattern depends on the assumed spectrum of IC waves, since a resonant wave-particle interaction is assumed. This is not specified in their paper, except through the wave interaction rate given as ν _sw = N _w Ω _s , where Ω _s is the gyrofrequency of ions of element s, and N _w is a constant of order 70. Equating this to the pitch diffusion coefficient, D = (π/4) Ω _s (δB²/B²), where δB is the magnetic field perturbation due to the wave, and B is the ambient magnetic field, we find δB/B ∼ 10.² With B ∼ 10 G and a density of order 10¹⁰ cm⁻³, the wave velocity amplitude is 2000 km s⁻¹. Of course these estimates should be treated with caution, because they are derived by applying quasi-linear theory well beyond its regime of validity, but the essential point that the wave energy requirements of this model are implausible remains. If the coronal ion cyclotron wave derived form a turbulent cascade, then even higher wave amplitudes should be found at lower frequencies, assuming for example a Kolmogorov spectrum. Loop resonant frequencies are lower than ion cyclotron frequencies by several orders of magnitude (typically 6–8), leading to a huge increase in the intensity of these waves if a −5/3 spectrum is assumed. Further, waves in the ion cyclotron frequency range rapidly damp by charge exchange reactions (e.g., Kulsrud and Pearce, 1969), with rate 1–100 s⁻¹, depending on the neutral fraction. Thus, waves traveling at the chromospheric Alfvén speed are damped after traveling a few km, increasing the energy requirements still further.

5.5 Summary

To summarize, while some of the models described above might come close to describing the solar FIP effect, they do so for rather contrived magnetic field geometries or for various other extreme assumptions. In all cases, except those of Antiochos (1994) and Schwadron et al. (1999), whose mechanisms both derive from the coronal response to energy deposition, no natural account of the difference between closed and open field is given. Further, none of the models appear capable of explaining the Inverse FIP Effect.

Given the relative success of Antiochos (1994) and Schwadron et al. (1999), it seems reasonable to pursue the byproducts of coronal heating as the key to the fractionation. Given the high frequency waves do not work due their energy requirements, and that lower frequency Alfvén waves carry far more of the wave energy, the next question to ask is how such waves could interact with chromospheric ions. Clearly, a resonant interaction is not possible, but such waves can interact nonresonantly through the ponderomotive force. This is discussed more fully in the following sections.

6 The Ponderomotive Force Model

6.1 Overview

We now turn to a description of our model of the FIP effect, which invokes the ponderomotive force due to magneto-hydrodynamic waves as the agent that separates ions from neutrals. Ponderomotive forces in magnetospheric and space plasmas are reviewed by Lundin and Guglielmi (2006). According to them, “Ponderomotive forces are time-averaged nonlinear forces acting on media in the presence of oscillating electromagnetic fields. The word ponderomotive comes from the Latin words pondus (ponderis) meaning “heaviness” and motor.” The complex dynamics of a system acting under Lorentz forces may be considerably simplified by averaging over the period of oscillations and described instead by ponderomotive forces. They can be seen to arise from the effects of wave refraction in an inhomogeneous plasma. In a nonmagnetic plasma, the refractive index, $-\sqrt \epsilon$, is given by $\epsilon = 1 - {\omega _p}^2/{\omega ^2}$, where ω _p is the plasma frequency. Waves are refracted to high refractive index, which means low plasma density. The increased wave pressure can then expel even more plasma from the low density region, leading to ducting instabilities. In magnetic plasma, $\epsilon = 1 - {\omega _p}^2/({\omega ^2} - {\Omega ^2})$ for linearly polarized parallel propagating transverse waves, where Ω is the ion cyclotron frequency. Thus, waves with ω ≪ Ω refract to high density regions, and plasma is attracted to regions of high wave energy density, especially when the energy and momentum of the waves are large. A simple expression for the ponderomotive force on an ion is derived below.

The refraction of waves to high density regions, and the corresponding attraction of ions to locations of high wave energy density when the wave pressure dominates over the thermal pressure of the ionized component of the plasma, means that the FIP effect depends crucially on details of wave propagation through the chromosphere. A high wave energy density in the corona will lead to a strong FIP effect. Weak coronal waves and strong waves lower down may lead to an inverse FIP effect, as chromospheric ions are attracted downwards. We will explore precise conditions under which these various phenomena may occur in more detail below.

We concentrate solely on the fractionation, referring the reader to the Living Reviews of Reale (2014) for the properties of plasma in closed coronal loops, and to Marsch (2006), Cranmer (2009) and Ofman (2010) for the physics of the acceleration of the fractionated gas into the fast and slow speed solar wind. In the subsections that follow, we discuss in detail the various components of the model. Figure 5 illustrates the basic scenario. We consider a coronal loop meeting the chromosphere at both footpoints. For the purposes of calculating the Alfvén wave propagation, we ignore the loop curvature. A variety of wave processes can occur at each footpoint, some illustrated at one and some illustrated at the other in the figure for clarity. A steady evaporative flow with speed much less than the local Alfvén speed is assumed to take material from the chromosphere to the corona. Such a flow arises from the chromospheric response to coronal heating, as heat is conducted downwards increasing the chromospheric temperature (e.g., Bray et al., 1991). Imada and Zweibel (2012) calculate evaporative upflows for a variety of coronal heating scenarios, and find upflows of order one to a few km s⁻¹ in the chromosphere, similar to previous work (Warren et al., 2002; Bray et al., 1991). We ignore transient effects, although in a magnetic filament heated episodically, these could play an important role. For instance, if Alfvén waves released by a coronal heating event reach the chromosphere before the heat conduction front, the chromospheric flow velocity under which the fractionation occurs will be much smaller than these estimates. In the opposite case, of heat conducting down before the Alfvén waves arrive, no fractionation could occur. More exotic cases where the Alfvén waves themselves carry the heat that causes the evaporation, for example in solar flares (Haerendel, 2009) are not considered here.

Figure 5:

Schematic diagram of model loop and wave processes, adapted from Laming (2012), which follows Hollweg (1984). All footpoint wave processes may happen at both footpoints, but are here split between the two for clarity. Alfvén waves shown as thick solid lines are assumed to be generated inside the coronal portion of the loop, and to bounce back and forth from the loop footpoints, with a probability of leaking out and being transmitted deeper into the chromosphere at each bounce (shown on left hand side). Approximately equal amplitudes of waves propagating in each direction result. Reflecting Alfvén waves can also generate slow mode (here labelled as “p-mode”) waves by a parametric process (shown on the right-hand side as thin dashed lines). Other acoustic waves (“p-modes” in helioseismology parlance) propagating within the solar envelope can mode convert to fast-mode waves upon reaching the chromospheric layer where the sound speed and Alfvén speed are equal (approximately where the plasma β = 1). The upgoing fast-mode waves (shown as thin solid lines) are refracted back downwards in the chromospheric region where the Alfvén speed increases with height. fast-mode wave may also mode convert to Alfvén waves and then propagate up to the loop to be reflected or transmitted, depending on the match between their frequency and the loop resonance. This provides an alternative means of seeding the loop with propagating Alfvén waves. Our non-WKB wave propagation calculations in fact follow an Alfvén wave being injected at one loop footpoint, being reflected or transmitted into the corona, and the successive bounces it undergoes. For waves at the loop resonance, this behaviour (without growth or damping included) is indistinguishable from waves generated within the loop itself, necessarily at the loop resonance or its harmonics.

In the absence of the ponderomotive force, we assume that the chromosphere is unfractionated, i.e., that sufficient turbulence exists to inhibit any gravitational settling of other forms of diffusion that might occur. A similar approach was taken by Hansteen et al. (1997). We suggest that the reflection and refraction of acoustic waves at discontinuities associated with chromospheric shock waves set up the conditions necessary for a turbulence. Interactions between oppositely directed waves lead to fluctuations of smaller and smaller size scales, right down to microscopic dimensions where mixing can occur. Following on from the discussion above, we neglect diffusion processes. Although the thermal force is expected to develop over a similar region to the ponderomotive force (the region of strong density and temperature gradients in the upper chromosphere), the acceleration associated with the thermal force is of order 1%–10% of the ponderomotive acceleration, and is negligible. The thermal acceleration is also dependent on 1/A, where A is the element atomic mass, unlike the ponderomotive acceleration which is mass independent, and can never produce an inverse fractionation as seen for example in the coronae of M dwarfs.

6.2 The ponderomotive force

An expression for the ponderomotive force is derived as follows, updated from Appendix A in Laming (2009). Consider the Lagrangian for a system of n particles with mass m and electromagnetic waves in a box of unit volume

$$L = \sum\limits_i {{1 \over 2}} {m_i}{({{\bf{v}}_{th,i}} + \delta {{\bf{v}}_i})^2} + \sum\limits_i {{{{q_i}} \over c}({{\bf{v}}_{th,i}} + \delta {{\bf{v}}_i}) \cdot \delta {\bf{A}} + {{ \epsilon \delta {{\bf{E}}^2} - \delta {{\bf{B}}^2}} \over {8\pi}},}$$

(1)

where v _th,i is the thermal speed and δv _i is the oscillatory speed induced by the wave of particle i, with mass m _i , and charge q _i . Wave electric and magnetic fields are given by δE and δB, respectively, δA is the wave vector potential, and c is the speed of light. We have chosen the radiation gauge where the electrostatic potential ϕ = 0. In any case, this is constant in an electrically neutral plasma (in the absence of electrostatic waves).

For Alfvén waves, energy is partitioned according to $\delta {B^2}/8\pi = \sum\nolimits_i {mv_{_{{\rm{osc}},i}}^2}/2 + \delta {E^2}/8\pi$. Also δB · B = 0, where B is the ambient magnetic field, and δv _i · δA = 0, not just on average but for all time. We also take the time average of v _th,i · δv _i = 0 and v _th,i · δA = 0 to find the Lagrangian

$$L = \sum\limits_i {{1 \over 2}} mv_{th,i}^2 + {{(\epsilon - 1)\delta {E^2}} \over {8\pi}} \rightarrow \sum\limits_i {{1 \over 2}mv_{th,i}^2} + \sum\limits_i {} {{q_i^2\delta E{{({z_i})}^2}} \over {2{m_i}(\Omega _i^2 - {\omega ^2})}},$$

(2)

where in the second line we have written $\epsilon - 1 = \omega _p^2/({\Omega ^2} - {\omega ^2}) = 4\pi n{q^2}/m\;({\Omega ^2} - {\omega ^2})$ and $(\epsilon - 1)\delta {E^2} \to \sum\nolimits_i {4\pi {q_i}^2\delta E{{({z_i})}^2}}/{m_i}\;({\Omega _i}^2 - {\omega ^2})$ for linearly polarized parallel propagating transverse waves. The “z” Euler-Lagrange equation for particle “i” gives

$${{\rm{d}} \over {{\rm{d}}t}}(m{v_{th,iz}}) = {{q_i^2} \over {2{m_i}}}{{\rm{d}} \over {{\rm{d}}z}}{{\delta {E^2}} \over {(\Omega _i^2 - {\omega ^2})}},$$

(3)

evaluating for the component of υ _th,i orthogonal to δA and δv _i . In uniform magnetic field, this is the same as the expression derived by Landau et al. (1984), and agrees with earlier work (e.g., Lee and Parks, 1983; Li and Temerin, 1993) if $\delta {E^2} = \delta {E_p}^2/2$, where δE _p is the peak electric field in the wave, giving a ponderomotive force

$${F_i} = {{q_i^2} \over {4{m_i}(\Omega _i^2 - {\omega ^2})}}{{{\rm{d}}\delta {E_p}{{({z_i})}^2}} \over {{\rm{d}}z}}.$$

(4)

When ω ≪ Ω _i , the ponderomotive acceleration is thus independent of ion mass, which is one crucial property relevant to obtaining an almost mass independent fractionation as observed. It is also independent of ion charge, so long as the ion is charged (and not neutral). Litwin and Rosner (1998) give a similar expression derived from the j × B and other second order terms in the MHD momentum equation. Away from the low frequency limit, circular polarized waves may give slightly different forces, with left and right circular polarization being different from each other as well as linear polarization (e.g., Nekrasov and Feygin, 2013). In nonuniform B in the low frequency limit, the ponderomotive force is given by

$${F_i} = {{{m_i}{c^2}} \over 4}{{\rm{d}} \over {{\rm{d}}z}}\left[ {{{\delta {E_p}{{({z_i})}^2}} \over {B{{({z_i})}^2}}}} \right],$$

(5)

which agrees with the first two terms in Eq. (2.6) of Lundin and Guglielmi (2006).

In fast-mode waves, energy is now partitioned according to $\delta {B^2}/8\pi + \delta {E_{th}} = \sum\nolimits_i {mv} _{{\rm{osc,}}i}^2/2 + \delta {E^2}/8\pi$, where δE _th is the wave thermal energy arising from compression and rarefaction. For the fast-mode wave δB · B = 0 only on average, but not instantaneously, though δv _i · δA = 0 remains unchanged. The thermal energy also time averages to zero, leaving the Lagrangian and ponderomotive force described by the same expressions as above. However, the extra longitudinal pressure associated with obliquely propagating fast-mode waves will reduce the eventual fractionation. See Sections 6.5 and 6.6 below.

With slow-mode waves, energy partitioning is similar to that for fast-mode waves. Whereas Alfvén and fast-mode waves always have δv ⊥ B, slow modes have δv∥ k. In parallel propagation the electric field, and hence a ponderomotive force capable of ion-neutral separation, are absent. Transverse electric field may arise with a slow-mode wave in parallel propagation along an isolated flux tube (a “sausage” mode) (e.g., Mikhalyaev and Solov’ev, 2005). We do not consider such possibilities further.

6.3 Chromospheric model

The ponderomotive force depends on the gradient of the wave transverse electric energy, $\partial \delta E_ \bot ^2/\partial z$. Since δE_⊥ = δυ_⊥B/c, such a gradient will develop where δυ_⊥ varies in response to varying chromospheric density. Previous (mainly analytic; e.g., Hollweg, 1984) works on wave propagation through the chromosphere have approximated the vertical density structure as exponential, with a scale height of order 200 km. While adequate for studying wave transmission into the corona, more detail is required for the FIP effect. The chromosphere is heated, presumably by means similar to those thought to heat the corona, and cooled in the region where most FIP fractionation occurs principally by radiation in H Lyman α. In this region where H starts to become ionized, its radiative cooling becomes increasingly inhibited and the temperature must rise. Correspondingly, the density drops, and the density gradient so produced is steeper than the typical hydrostatic scale height elsewhere. Consequently, the region of the chromosphere where the FIP fractionation has long been assumed to occur, i.e., the region where H becomes ionized, is highly likely to be a region with a strong density gradient due to the physics of radiative cooling, and hence a location where the ponderomotive force will be strongest. Figure 6 shows this structure in the left panel, taken from the empirical model (C7) of Avrett and Loeser (2008), an update to the older VALC model (Vernazza et al., 1981).

Figure 6:

Left: Empirical model of the solar chromosphere plotted from data given in Avrett and Loeser (2008). The density is the solid black line, to be read on the left axis, while the temperature is the dashed gray line, to be read on the right axis. The ordinate (“distance along the loop”) is the altitude above the photosphere. The steep density gradient at 2150 km altitude is where strong ponderomotive force can develop. Right: Force-free magnetic field structure calculated in Rakowski and Laming (2012) following Athay (1981). Altitude is given by the y-axis. The x-axis give lateral expansion. The dashed lines show contours of the Alfvén speed. In this plot the plasma β = 1 layer is at an altitude of approximately 650 km in the Sun. Images reproduced with permission from Rakowski and Laming (2012), copyright by AAS.

The right panel of Figure 6 shows the model magnetic field. Altitude here is given by the y-axis. The x-axis gives lateral expansion on the same scale. The dashed lines show contours of the Alfvén speed. The magnetic field emerges from the photosphere in tight fibrils. At the atmospheric layer, typically in the low chromosphere, where gas pressure and magnetic pressure are equal, the field begins to expand and fill the whole volume. In Figure 6 (right panel) this corresponds to y = 650 km approximately. In the real Sun, this occurs at altitudes typically between 400 and 800 km, depending on the magnetic field strength. The total magnetic field expansion from y = 600 km upwards in this model is a factor of 5, similar to that suggested by Gary (2001).

Observations of hard X-ray bremstrahlung during flares with RHESSI (Lin et al., 2004) corroborate many of these features (Kontar et al., 2008; Saint-Hilaire et al., 2010). An average scale density scale height of 130–140 km is derived. Kontar et al. (2008) infer chromospheric flux tube expanding in radius by a factor of 3 at an altitude between 900 km and 1200 km. This would imply magnetic field decreasing by a factor of 9, albeit at a higher height than suggested above.

Avrett and Loeser (2008) also give an empirical electron density coming from the ionization balance for H, from which we calculate the ionization balance for all other elements of interest. Collisional processes (ionization, radiative and dielectronic recombination) are all taken from the tabulations provided by Mazzotta et al. (1998). Subsequent refinements to the ionization and dielectronic recombination rates as implemented by Bryans et al. (2009) are not crucial here, since our concern is only with neutrals and singly ionized species, but the suppression of dielectronic recombination by finite density effects (Nikolić et al., 2013) is important and is now included as an update to previous calculations (Laming, 2009, 2012). We also include charge exchange ionization using rates given by Kingdon and Ferland (1996), updated and amended as detailed in Laming (2012). This treats the capture by a free proton of an electron from an initially neutral atom. It is most important for O, and helps lock the O ionization balance to that of H, but can be of significance for other low FIP elements as well. In the Avrett and Loeser (2008) model, H begins to become ionized at heights between 1000–1500 km, reaching about 50% ionization at 2000 km. For comparison, Saint-Hilaire et al. (2010) infer a unit step change in ionization level at a height of 1.3 ± 0.2 Mm.

We evaluate photoionization rates using incident spectra based on Vernazza and Reeves (1978) with the extensions and modifications outlined in Laming (2004a). In most cases, the “quiet region” spectrum is used. An additional contribution from trapped Lyman α in regions where this line is optically thick is also included, with approximate flux ∫ n_H dl AC _ex /(A + τC _{de −ex}), where ∫ n_H dl is the column density of H atoms, τ = σ ∫ n_H dl is the opacity in terms of the absorption cross section α at line centre, A is the upper level decay rate, and C _ex and C _{de −ex} are the collisional excitation and de-excitation rates for the upper level. We take photoionization cross sections from the compilation of Verner et al. (1996). Our ionization balance so computed is necessarily a steady state model, but is based on the empirical electron density found by Avrett and Loeser (2008), which is higher than that which we would compute based on their inferred chromospheric temperature. Carlsson and Stein (2002) study the effects of dynamic ionization of H, and find that the passage of shock waves through the chromosphere does indeed increase the electron density over that coming from simple photoionization-recombination equilibrium for H. Individual photoionization and recombination rates however are too slow for the ionization balance to respond to individual shock waves. The elevated electron density instead represents a time averaged response to the dynamics, and is itself quasi-steady state. Wedemeyer-Böhm and Carlsson (2011) consider the Ca⁺ to Ca²⁺ ionization balance. It is more variable than that between H and H⁺, but is of less concern to us, since the ponderomotive force experienced by an ion is independent of ion charge, so long as the wave frequency is much lower than the ion gyrofrequency.

In isolation, the action of the ponderomotive force would produce a local abundance variation close to the region where it is strongest, around chromospheric altitudes of 2150 km. A region where low FIPs are depleted by the upwards acceleration would sit below this altitude, and above it a region of FIP enhancement. A coronal abundance anomaly would not result without either a flow through the chromosphere, or diffusion (in a static case). The typical timescales associated with such processes would be H _D /υ ∼ 2 × 10⁷/10³ ∼ 2 × 10⁴ s where H _D is the density scale height and υ the flow velocity lower down in the chromosphere, or $H_D^2/D \sim 4 \times {10^{14}}/6 \times {10^9}\sim6 \times {10^4}$ where D is the diffusion coefficient for low FIP ions in a neutral H atmosphere. Both timescales evaluate to several hours to days, similar to that observed (Widing and Feldman, 2001), as do similar timescales evaluated for the coronal loop. The chromospheric response may be altered by the mixing induced by turbulence associated with shocks in the lower chromosphere (e.g., Reardon et al., 2008), and so the coronal diffusion is likely to be the controlling timescale. We do not consider such processes further, restricting ourselves to a steady state chromosphere and upward flow speed, and emphasizing again that collisional coupling in the chromosphere is crucial to the coronal abundance anomaly, since it is the source for the extra low FIP ions. Once collisionless (in the solar wind) no further bulk fractionation can occur. A local FIP enhancement must be accompanied by another local depletion, since the collisional coupling to the lower solar atmosphere has been lost.

6.4 The Alfvén wave transport equations

Alfvén wave propagation is often treated in the Wentzel-Kramers-Brillouin (WKB) approximation, where it is assumed that the wavelength is much shorter than the typical length scale of inhomogeneities, and hence that the effects of reflection and refraction can be neglected. This is emphatically not the case in the solar chromosphere. Since the ponderomotive force depends on the spatial variation of the Alfvén wave electric field in the inhomogeneous plasma of the chromosphere, a direct integration of the transport equations is required. We evaluate this spatial variation paraphrasing and updating the treatment in Appendix B of Laming (2009). We start from the linearized MHD force and induction equations,

$$\rho {{\partial \delta {\bf{v}}} \over {\partial t}} + \rho ({\bf{u}} \cdot \nabla)\delta {\bf{v}} + (\delta {\bf{v}} \cdot \nabla)\rho {\bf{u}} = {{(\nabla \times \delta {\bf{B}}) \times {\bf{B}}} \over {4\pi}} = {{({\bf{B}} \cdot \nabla)\delta {\bf{B}} - (\nabla \delta {\bf{B}}) \cdot {\bf{B}}} \over {4\pi}},$$

(6)

and

$$\matrix{{{{\partial \delta {\bf{B}}} \over {\partial t}} = \nabla \times (\delta {\bf{v}} \times {\bf{B}}) + \nabla \times ({\bf{u}} \times \delta {\bf{B}})} \hfill \cr {\quad \quad \, = - {\bf{B}}\nabla \cdot \delta {\bf{v}} - (\delta {\bf{v}} \cdot \nabla){\bf{B}} + ({\bf{B}} \cdot \nabla)\delta {\bf{v}} - \delta {\bf{B}}\nabla \cdot {\bf{u}} - ({\bf{u}} \cdot \nabla)\delta {\bf{B}} + (\delta {\bf{B}} \cdot \nabla){\bf{u}},} \hfill \cr}$$

(7)

where u and B are the unperturbed velocity and magnetic field, δv and δB are the perturbations, and ρ is the density. Equation (6) is rewritten using (∇δB) · B = ∇ (B · δB) − (∇B) · δB to yield

$${{\partial \delta {\bf{v}}} \over {\partial t}} + ({\bf{u}} \cdot \nabla)\delta {\bf{v}} = {{\bf{V}}_A} \cdot \nabla \left({{{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}} \right) + {{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}{{{{\bf{V}}_A} \cdot \nabla \rho} \over {2\rho}} + {{(\nabla {\bf{B}}) \cdot \delta {\bf{B}}} \over {4\pi \rho}} - {{(\delta {\bf{v}} \cdot \nabla)(\rho {\bf{u}})} \over \rho},$$

(8)

where ${{\bf{V}}_A} = {\bf{B}}/\sqrt {4\pi \rho}$ is the Alfvén velocity, and we have assumed B · δB = 0 for Alfvén waves and parallel propagating fast modes.

Specializing to plane Alfvén waves, we write (∇B) · δB = (∂B _x /∂x) δB = − (∂B _z /∂z) δB/2 since ∇ · B = 0 (assuming ∂B _x /∂x = ∂B _y /∂y in cylindrical symmetry, with $\delta {\bf{B}} = \delta B{\bf{\hat x}}$, where ${\bf{\hat x}}$ is a unit vector along the x-axis). Similarly, (δv · ∇) (ρu) = δυ _x ∂ (ρu _x )/∂x = −δυ _x ∂ (ρu _z )/∂z/2 since ∇ · (ρu) = 0, and using ∂ (ρu _z /B _z )/∂z = 0 gives

$${{\partial \delta {\bf{v}}} \over {\partial t}} + ({\bf{u}} \cdot \nabla)\delta {\bf{v}} = {{\bf{V}}_A} \cdot \nabla \left({{{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}} \right) + {{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}{{{{\bf{V}}_A}} \over {2{H_D}}} - {{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}{{{V_A}} \over {2{H_B}}} + \delta {\bf{v}}{u \over {2{H_B}}}.$$

(9)

Here, 1/H _B = ∂ ln B _z /∂z, 1/H _D = ∂ ln ρ/∂z, and below 1/H _A = ∂ ln V _A /∂Z.

Similar manipulations using ∇ · u = −u · ∇ρ/ρ = −υ/H _D and assuming ∇ · δv = 0 give the induction equation in the form

$${\partial \over {\partial t}}\left({{{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}} \right) + ({\bf{u}} \cdot \nabla){{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}} = ({{\bf{V}}_A} \cdot \nabla)\delta {\bf{v}} + {{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}{u \over {2{H_D}}} + \delta {\bf{v}}{{{V_A}} \over {2{H_B}}} - {{\delta {\bf{B}}} \over {\sqrt {4\pi \rho}}}{u \over {2{H_B}}}.$$

(10)

Taking Eq. (9) plus or minus Eq. (10) and rearranging gives the final result,

$${{\partial {I_ \pm}} \over {\partial t}} + (u \mp {V_A}){{\partial {I_ \pm}} \over {\partial z}} = (u \pm {V_A})\left({{{{I_ \pm}} \over {4{H_D}}} + {{{I_ \mp}} \over {2{H_A}}}} \right),$$

(11)

where ${I_ \pm} = \delta {\bf{v}} \pm \delta {\bf{B}}/\sqrt {4\pi \rho}$, representing waves propagating in the ∓ z-directions. We have focussed on plane polarized Alfvén waves. Clearly, circularly polarized Alfvén waves will obey the same transport equations, as do torsional waves in cylindrical coordinates. These different wave polarizations may still produce subtly different fractionations, due to their different couplings to other wave modes. The case of parametric generation of slow-mode waves is discussed below.

Such transport equations have been presented in several different forms by various authors. Cranmer and van Ballegooijen (2005) review these in their Appendix B and demonstrate their equivalence. We have assumed a cylindrically symmetrical magnetic field above. One could easily generalize this treatment to incorporate Alfvén wave transport on arbitrary (i.e., observed or extrapolated) magnetic field lines for a more realistic description of observations. We have also restricted treatment to field aligned wave propagation, rendering the waves incompressible. For plane and circularly polarized waves this amounts to assuming that the wave follows the field line on which it propagates. For torsional waves on a flux tube, it requires that the flux tube magnetic field have no B _ϕ component. In the case that this is not so, the torsional wave is inevitably of mixed Alfvén/fast mode polarization and has B · δB ≠ 0. In this case, Eqs. (11 are augmented by extra terms such as −∇ (B · δB)/4πρ ∓ V _A ∇ · δv on the right-hand side.

In integrating Eqs. (11), we put ∂I_±/∂t = iωI_± to derive four coupled equations for the real and imaginary parts of I_±. Equations (11) are integrated from a starting point in the left hand side chromosphere where Alfvén waves leak down into the chromosphere, back through the corona to the right-hand side where waves are fed up from below. In this way the reflection and transmission of Alfvén waves at the loop footpoints and elsewhere is naturally reconstructed. The velocity and magnetic field perturbations are calculated from

$$\matrix{{\quad \;\,\delta v = {{{I_ +} + {I_ -}} \over 2}} \hfill \cr {{{\delta B} \over {\sqrt {4\pi \rho}}} = {{{I_ +} - {I_ -}} \over 2}.} \hfill \cr}$$

(12)

The wave energy density and positive and negative going energy fluxes are

$$\matrix{{U = {{\rho \delta {v^2}} \over 2} + {{\delta {B^2}} \over {8\pi}} = {\rho \over 4}(I_ + ^2 + I_ - ^2)} \hfill \cr {{F_ +} = {\rho \over 4}I_ + ^2{V_A}} \hfill \cr {{F_ -} = {\rho \over 4}I_ - ^2{V_A},} \hfill \cr}$$

(13)

and the wave peak electric field appearing in equation 4 is

$$\delta E_p^2 = {{{B^2}} \over {2{c^2}}}(I_ + ^2 - I_ - ^2).$$

(14)

6.5 Fractionation

We recap and expand the treatment given in Laming (2004a). Our model starts with a fully mixed chromosphere, upon which pondermotive forces due to Alfvén wave reflection and transmission act to provide the fractionation. The low solar chromosphere is of much higher density than the upper layers where the FIP fractionation will occur in our models. Consequently the lower boundary condition of completely mixed photospheric composition material gives an essentially infinite particle “reservoir” to supply the extra fractionated elements. To calculate the fractionation, we follow in part the approach and notation of Schwadron et al. (1999). Consider first the motion of ions and neutrals of element s in a background flow of protons and hydrogen with speed u. We neglect the ambipolar force, which is generally much less than gravity. We also neglect an inertial term $\partial/\partial z({\rho _s}u_s^2/2)$, since the flow speed will turn out to be much lower than the particle thermal speeds. Then the momentum equations for ions and neutrals are

$${{\partial {P_{si}}} \over {\partial z}} = - {\rho _{si}}g - {\rho _{si}}{\nu _{si}}({u_{si}} - u)$$

(15)

$${{\partial {P_{sn}}} \over {\partial z}} = - {\rho _{sn}}g - {\rho _{Sn}}{\nu _{sn}}({u_{sn}} - u),$$

(16)

where P _si and P _sn are the partial pressures of ions and neutrals of element s, ρ _si and ρ _sn are the corresponding densities, ν _si and ν _sn the collision rates with ambient gas (assumed hydrogen and protons), u _si and u _sn the flow speeds, and u the hydrogen flow speed imposed on the loop. Detailed expressions for ν _si and ν _sn are given in Laming (2004a). The partial pressures are given by ${P_{s,i,n}} = ({k_B}T/{m_s} + v_{{\rm{turb}}}^2 + v_{{\rm{wave}}}^{\rm{2}}){\rho _{s,i,n}}/2$, where the various terms on the right-hand side represent the particle thermal speed, the microturbulent velocity coming from the chromospheric model, and the particle motion in longitudinal (i.e., acoustic) waves, either induced by the Alfvén waves themselves, or propagating up from the photosphere. These are discussed in more detail in the next subsection. In true collisionless plasma, neutrals would not respond to the wave. However, the solar chromosphere is sufficiently collisional that neutrals move with the ions in the wave motion (e.g., Vranjes et al., 2008) for wave frequencies well below the charge exchange rate that couples neutrals and ions, and so neutrals require the same form for their partial pressure as the ions. We also neglected inertial terms above. Inclusion of such terms would lead to

$${P_{si,n}} = ({k_{\rm{B}}}T/{m_s} + v_{{\rm{turb}}}^2 + v_{{\rm{wave}}}^2 + u_s^2){\rho _{si,n}}/2 = v_s^2{\rho _{si,n}}/2$$

(17)

assuming u _si − u _sn ≪ u _s ∼ u.

The momentum equations are combined by forming ν _sn ∂P _si /∂z + ν _si ∂P _sn /∂z to yield

$${{\partial {P_s}} \over {\partial z}} = - {\rho _s}g - {\nu _{{\rm{eff}}}}{\rho _s}({u_s} - u) + {{\partial {\xi _s}} \over {\partial z}}{{{\rho _s}v_s^2} \over 2}{{{\nu _{si}} - {\nu _{sn}}} \over {(1 - {\xi _s}){\nu _{si}} + {\xi _s}{\nu _{sn}}}},$$

(18)

with ν_eff = ν _si ν _sn /(ξ _s ν _sn + (1 − ξ _s ) ν _si ) and ξ _s being the ionization fraction of element s. For

$${u_s} = u - g/{\nu _{{\rm{eff}}}}(1 - \mu/{m_s}) + \partial {\xi _s}/\partial z(v_s^2/2)({\nu _{si}} - {\nu _{sn}})/{\nu _{si}}/{\nu _{sn}},$$

(19)

where μ is the mean molecular weight, all elements are lifted by the background flow to the same scale height given by k_BT/μg. This obviously requires uν_eff > g, assuming the term in ∂ξ _s /∂z negligible. Generally, u − g/ν_eff (1 − μ/m _s ) ∼ 10³ cm s⁻¹ or more, while ${{\partial {\xi _s}} \over {\partial z}}\sim{10^{ - 8}}{\rm{c}}{{\rm{m}}^{{\rm{ - 1}}}}$ and ${{{\rho _s}v_s^2} \over 2}({\nu _{si}} - {\nu _{sn}})/{\nu _{si}}/{\nu _{sn}}\sim{10^9}{\rm{c}}{{\rm{m}}^{\rm{2}}}{{\rm{s}}^{{\rm{ - 1}}}}$. For uν _s ≪ g, we get gravitationally stratified solutions with ρ _s ∝ exp (−m _s gz/k_BT). With g = 2.74 × 10⁴ cm s⁻², and ν _s ∼ 10²–10³ the former case is valid for the Sun for flow speeds in the chromosphere greater than a relatively modest 10–100 cm s⁻¹. Laming (2012) considers the upward flow speed due to chromospheric evaporation, and finds speeds of at least 10³ cm s⁻¹.

A gravitational settling timescale may be estimated from Eqs. (15) and (16). We write $\partial {P_s}/\partial z \simeq c_S^2\partial {\rho _s}/{\partial _z} \simeq (c_S^2/{u_{{\rm{sett}}}})\partial {\rho _s}/\partial t$, where the sound speed is c _S and the settling speed u_sett ∼ g/ν_eff. Integrating with respect to t gives $t \sim c_S^2{v_{{\rm{eff}}}}/{g^2} \sim {10^4}({n_H}/{10^{10}})/A\;{\rm{s}}$, where A is the atomic mass of element s, assuming that ν_eff is dominated by collisions with neutral H. The settling time increases with the density as one moves deeper into the chromosphere, and with the presence of turbulence with amplitude added in quadrature to c _S , and can easily be on the order of days or weeks or more. Higher in the chromosphere, ν_eff will be dominated by collisions with protons, and a longer timescale would result as the chromospheric density approaches 10¹⁰ cm⁻³.

The solar chromosphere is doubtless a more dynamic environment than represented by Eqs. (16)–(19). For our purposes the net result of this dynamic behavior is assumed to completely mix up the plasma to give uniform elemental composition with height, which is obtained in our model with the above choice for ν _s . Other choices may be possible which would provide chemical fractionation in the unperturbed chromosphere, and one could choose ν _s to provide the required FIP effect. However, the physics behind such a specification for ν _s in most cases remains obscure, and is probably unrealistic, leading to an unsatisfactory explanation for the FIP effect.

We now include a ponderomotive force, ρ _si a on the ions in the momentum equations;

$${{\partial {P_{si}}} \over {\partial z}} = - {\rho _{si}}g - {\rho _{si}}{\nu _{si}}({u_{si}} - u) + {\rho _{si}}a$$

(20)

$${{\partial {P_{sn}}} \over {\partial z}} = - {\rho _{sn}}g - {\rho _{sn}}{\nu _{sn}}({u_{sn}} - u).$$

(21)

Again writing ${P_s} = {\rho _s}c_S^2$, taking u _s as specified above and integrating with respect to z, we find

$${{{\rho _s}({z_u})} \over {{\rho _s}({z_l})}} = \exp \left\{ {2\int_{{z_l}}^{{z_u}} {{{{\xi _s}a{\nu _{{\rm{eff}}}}} \over {{\nu _{si}}v_s^2}}{\rm{d}}z}} \right\},$$

(22)

where the constant of integration has been chosen to keep ρ _s (z _u ) = ρ _s (z _l ) when a = 0. A quantitative assessment of coronal element abundances anomalies requires an evaluation of Eq. (22) with a realistic model chromosphere in the region of Alfvén wave reflection, with a coming from Eq. (5).

As will be seen below, most the the FIP fractionation develops over a small range in z, where the ponderomotive acceleration a is strong. The timescale to establish this local abundance anomaly is short, basically (z _u − zl)/u ∼ (10⁶–10⁷)/10⁴ ∼ 10³ s. By itself, the ponderomotive force would only produce a deficit of low FIP ions just below this region, and a surplus just above. To produce the fractionation seen in coronal loops and the solar wind, thermal transport or diffusion processes must continually supply further low FIP ions from below to erase the deficit, and communicate the resulting fractionation above to still higher levels of the solar atmosphere. Thus, while the fractionation can be produced locally rather quickly, and is therefore immune from processes that would otherwise disrupt fractionation produced solely by diffusive processes, the timescale to change the composition of a coronal loop is still on the order of days, as observed (Widing and Feldman, 2001) due to the necessity of thermal transport of the fractionation.

6.6 Compressional chromospheric waves

6.6.1 Introduction

We have introduced an extra longitudinal pressure associated with the Alfvén waves proportional to $c_{{\rm{wave}}}^2$ [see Eq. (17)], which has the effect of causing some saturation of the FIP fractionation. Here we give some physical motivations for this extra term. It has three possible sources. The first is the inevitable generation of slow-mode waves by the Alfvén driver. Physically, the periodic variation in magnetic pressure of the Alfvén wave drives longitudinal compressional waves. These generated acoustic waves can act back on the Alfvén driver, as the compressional wave introduces a periodic variation in the Alfvén speed, which generates new Alfvén waves. The second will be obliquely propagating fast-mode waves, which are necessarily compressive. Torsional Alfvén wave on a twisted magnetic flux tube are inevitably mixed with the kink mode, and hence are compressive. The third relates to acoustic waves propagating up to the chromosphere from the convection zone.

6.6.2 Parametric generation by Alfvén waves

Following Laming (2012), we illustrate the generation of slow mode or acoustic waves by the pon-deromotive force associated with plane Alfvén waves with a simple 1D calculation. The linearized momentum equation keeping terms to all orders in perturbed quantities is (all symbols have their usual meanings as defined above),

$$(\rho + \delta \rho){{\partial \delta {v_z}} \over {\partial t}} + (\rho + \delta \rho)\delta {v_z}{{\partial \delta {v_z}} \over {\partial z}} = (\rho + \delta \rho){\partial \over {\partial z}}{{\delta {B^2}} \over {(\rho + \delta \rho)}} - {{\partial \delta P} \over {\partial z}} - g\delta \rho,$$

(23)

where

$$\matrix{{\quad \delta \rho = - \rho \nabla \cdot \delta {\bf{r}} - \delta {r_z}{{\partial \rho} \over {\partial z}} = - \rho \delta {\bf{r}}\left({i{k_S} + {1 \over {{H_D}}}} \right)} \hfill \cr {\delta P = - \gamma P\nabla \cdot \delta {\bf{r}} - \delta {r_z}{{\partial P} \over {\partial z}} = - P\delta {\bf{r}}\left({i{k_S}\gamma + {1 \over {{H_P}}}} \right),} \hfill \cr}$$

(24)

for Eulerian displacement δr ∝ exp i (ω _S t + k _S z), where H _P = P/(∂P/∂z) and H _D = ρ/ (∂ρ/∂z) (signed) pressure and density scale heights, respectively. The first term on the right-hand side of Eq. (23) represents the instantaneous ponderomotive force. In cases, where the WKB approximation applies, SB ∝ ρ^1/4, and this expression is equivalent to the more usual form −∂ (δB²/8π)/∂z. Substituting for δρ and δP from Eqs. (24), keeping terms as high as second order in small quantities, Eq. (23) becomes

$$ - i{{{\omega _S}} \over {{H_D}}}\delta v_z^2 + \left({ - \omega _S^2 + k_S^2c_S^2 - i{{{k_S}c_S^2} \over {{H_P}}} - {{c_S^2} \over {\gamma H_P^2}} - i{{{k_S}c_S^2} \over {\gamma {H_P}}} - i{k_S}g - {g \over {{H_D}}}} \right)\delta {v_z} - i{\omega _S}{\partial \over {\partial z}}{{\delta {B^2}} \over {8\pi \rho}} = 0.$$

(25)

This is considerably simplified in isothermal conditions, γ = 1, $\gamma = 1,{H_P} = {H_D} = - c_S^2/g$, so that

$$ - i{{{\omega _S}} \over {{H_D}}}\delta v_z^2 + (- \omega _S^2 + k_S^2c_S^2 + i{k_S}g)\delta {v_z} - i{\omega _S}{\partial \over {\partial z}}{{\delta {B^2}} \over {8\pi \rho}} = 0.$$

(26)

We put $\Im {k_S} = - g/2c_S^2$, and $\sqrt {(\Re {k_S}) + {g^2}/4c_S^4} = 2\Re {k_A}/n,\;\omega = 2{\omega _A}/n$, where k _A and ω _A are the wavevector and angular frequency of the Alfvén wave with n = 1, 2, 3,.. (anticipating the result below). We find

$$\delta v_z^2 - \delta {v_z}i{H_D}{\omega _S}\left({1 - {{c_S^2} \over {V_A^2}}} \right) + {H_D}{\partial \over {\partial z}}{{\delta {B^2}} \over {8\pi \rho}} = 0$$

(27)

with solution

$$\delta {v_z} = {{ - i} \over 2}\left[ {\sqrt {\delta v_A^2 + H_D^2\omega _S^2{{\left({1 - {{c_S^2} \over {V_A^2}}} \right)}^2}} - {H_D}{\omega _S}\left({1 - {{c_S^2} \over {V_A^2}}} \right)} \right],$$

(28)

where we have put ${\partial \over {\partial z}}(\delta {B^2}/8\pi \rho) = (\delta {B^2}/4\pi \rho)/4{H_D} = \delta v_A^2/4{H_D}$ using the WKB result for Alfvén waves in a density gradient, and assuming 1/H _D ≫ ℜk _A . When $c_S^2 \sim V_A^2$ or H _D → 0, δυ _z ≃ −iδυ _A /2. In the opposite limit $\delta {v_z} \simeq - i\delta v_A^2/4{H_D}{\omega _S}(1 - c_S^2/V_A^2)$. In these two cases ω _S = ω _A or ω _S = 2ω _A , respectively. In fact, acoustic waves can be generated with ω _S = 2ω _A /n, with higher n becoming more intense as the nonlinearity increases (Landau and Lifshitz, 1976). This is shown explicitly by Laming (2012), who extends the treatment above to include higher powers of δυ _z . Vasheghani Farahani et al. (2011) treat the case of slow-mode wave generation by a torsional Alfvén wave. This is subtly different to the case of a plane Alfvén wave considered here, and the FIP fractionation resulting from such a model will be investigated in future work.

When the Alfvén wave becomes evanescent in a sufficiently steep density gradient, k _A − iκ _A and

$$\delta {v_z} = {{ - i} \over 2}\left[ {\sqrt {\delta v_A^2 + H_D^2\omega _S^2{{\left({1 - {{\kappa _A^2c_S^2} \over {\omega _A^2}}} \right)}^2}} - {H_D}{\omega _S}\left({1 + {{\kappa _A^2c_S^2} \over {\omega _A^2}}} \right)} \right],$$

(29)

resulting in reduced δυ _z compared to the case with propagating Alfvén waves. This will be apparent in results to be presented in Section 7.

6.6.3 Fast-mode waves from above

The treatment of Vasheghani Farahani et al. (2011) also considers a second source of longitudinal pressure. Torsional waves on a flux tube with magnetic twist are no longer pure Alfvén waves, but have an admixture of fast mode or kink polarization. Since the magnetic perturbation (in the ϕ direction in cylindrical polar coordinates) now has a component along the background magnetic field (the twist gives it a ϕ component also), the wave becomes compressive. This is also true more generally of any fast-mode wave in oblique propagation, and in Laming (2009) it was shown that such longitudinal pressure would lead to a natural saturation of the FIP effect at high wave amplitudes. In the case where transverse and longitudinal pressures are equal, the FIP effect saturates at the commonly observed value of about 4. However, such compressive waves are also subject to increased damping, and are therefore less likely to develop to large amplitudes. The existence or otherwise of twisted magnetic loops in the corona is also controversial. Accordingly, we do not consider such possibilities further in this review.

6.6.4 P-modes from below

The third contribution to the longitudinal pressure in the chromosphere comes from the continued propagation upwards of slow modes waves or shocks developing from turbulence lower down in the atmosphere. We include a longitudinal pressure with amplitude 6.25 km s⁻¹ motivated by the simulations in Heggland et al. (2011). The velocity amplitude of these waves would be expected to grow with altitude, due to WKB effects, although some reflection back downwards may also occur, and should damp mainly due to the effect of radiation. The principal coolant in the photosphere is H⁻, with cooling timescale τ ≃ (1.2 × 10¹¹/n _e )(5000 K/T)² minutes (Ayres and Rabin, 1996). Cooling of a similar magnitude will be present in the low chromosphere, although different processes may also contribute. Although the plasma density varies, throughout large sections of the chromospheric model, the electron density and temperature are roughly constant and of order 10¹¹ cm⁻³ and 5000 K, respectively, leading to a constant cooling time of order 1 minute. Thus, for 3 minute or 5 minute waves, the product ωτ ∼ 1, and the wave decay length would be comparable to the wavelength (Mihalas and Weibel-Mihalas, 1984), and similar to the WKB growth. In fact, the simulations of Heggland et al. (2011) show approximately constant slow-mode wave amplitude with height for a variety of models, as do the observations of Beck et al. (2013, albeit at a lower wave amplitude), so we accordingly adopt a constant slow-mode wave amplitude in our models.

While slow-mode waves reduce the fractionation by increasing $v_s^2$ in the denominator of the integrand in Eq. (22), when these steepen into shock waves, we expect fractionation to cease altogether due to the extra turbulence. Accordingly, we also neglect fractionation at chromospheric altitudes where the slow-mode wave amplitudes added in quadrature come to a value greater than the local sound speed. The rationale for this is that in such conditions, a shock will form, and the mixing produced by turbulence generated in such conditions would preclude further fractionation. Reflection and refraction of sound waves at the discontinuity will produce oppositely directed packets of sound waves which can initiate a cascade to smaller, and ultimately microscopic, spatial scales, assumed to induce microscopic mixing. This has the effect in most models of limiting FIP fractionation to the upper regions of the chromosphere.

7 Results and Interpretation

7.1 Closed loop

As a first illustration of the action of the ponderomotive force in causing FIP fractionation, we consider the case of a closed magnetic loop. The model loop is taken to be 100 000 km long, and plasma in the loop has a density scale height of 125 000 km, extrapolated upwards from the chromospheric model. The coronal temperature is constant at the maximum temperature of the chromospheric temperature (∼ 1.6 × 10⁶ K) but this value is not significant since we are uninterested in the ionization balance in this region and the Alfvén wave propagation only depends on the density. The coronal magnetic field is 20 G, increasing by a factor of 5 in the photosphere, as in Figure 6 (right panel). The chromospheric model is taken from Avrett and Loeser (2008), and the plasma β = 1 layer is at 615 km altitude above the photosphere. We simply treat the parallel propagation of undamped shear Alfvén waves. With reference to Figure 5, the solution of Eqs. (11) is started with a downgoing wave at the left-hand chromosphere, and then integrated back to the chromosphere at the other end of the loop. Choosing a wave angular frequency of 0. 07 s⁻¹ means the wave is on resonance with the coronal loop, and in our calculation, 98% of the upgoing wave energy from the right-hand chromosphere is transmitted to the corona. Hence the chromospheric wave patterns in both chromospheres are very similar, with the roles of upgoing and downgoing waves interchanged (with 100% transmission, they would be identical). The ponderomotive force is insensitive to the direction of wave motion, and so is the same at each footpoint.

Figure 7 shows the solution for the coronal portion of the loop. The top panel shows δv and $\delta {\bf{B}}/\sqrt {4\pi \rho}$ [Eqs. (12)], real components in black, imaginary components in grey. The middle panel shows the wave energy fluxes, left and right going, and their difference, divided by the magnetic flux density. Normalized thus, this difference should be constant in the absence of wave growth or damping, and provides a check on energy conservation in the integration. The bottom panel shows the ponderomotive acceleration, a, calculated from Eqs. (5) and (14). Throughout the corona (2500 km < z < 97500 km), a ≪ 2.7 × 10⁴ cm s⁻², the solar gravitational acceleration. In the chromospheric footpoints, a is much larger.

Figure 7:

Solution for the coronal portion of the loop. The top panel shows δv and $\delta {\bf{B}}/\sqrt {4\pi \rho}$ [Eqs. (12)], real components in black, imaginary components in grey. The middle panel shows the wave energy fluxes, left and right going, and their difference, divided by the magnetic flux density. Normalized thus, this difference should be constant in the absence of wave growth or damping, and provide a check on energy conservation in the integration. The bottom panel shows the ponderomotive acceleration, a.

Figure 8 illustrates important features of the solution in the chromospheric portion of the loop. The top and bottom panels on the left hand side show the same variables as the top and bottom panels in Figure 7 (the wave energy fluxes are not shown). The ponderomotive acceleration shows a large “spike” at an altitude of 2150 km, coinciding with the steep chromospheric density gradient shown in Figure 6 (left panel). Also shown on the bottom left panel is the amplitude of slow-mode waves arising from parametric generation by the Alfvén driver, shown as a dotted line. This is added in quadrature to the amplitude of slow-mode waves propagating upwards from the photospheric, assumed here to be a constant 6.25 km s⁻¹, following the discussion in Section 6.3. This value is also consistent with the macroscopic velocity field inferred in the solar chromosphere by Vieytes et al. (2005, see their Figure 3ab). The parametric slow mode amplitude goes through a sharp minimum where the chromospheric density gradient is steepest at about 2150 km altitude. Rakowski and Laming (2012) show that this occurs where the Alfvén wave becomes evanescent. The panels on the right-hand side show the chromospheric ionization balance and FIP fractionation for selected elements. The bottom panel shows FIP fractionation for the abundance ratios S/O, He/O, Mg/O, Fe/O and Si/O, with the linestyles indicated as black lines, to be read on the left axis. One can see Fe/O and Mg/O fractionating to a value close to 4, Si/O to 2.6. S/O to 1.6 and He/O to 0.4. The ionization balance is shown as grey lines with the same linestyles for Fe, Mg, Si, S, C, and He. Also shown are charge states fractions for H and O as labelled. The ionization balances for Fe, Mg, Si, C, and S are hard to distinguish on this plot, so the top right panel shows these in more detail, with the charge fraction scale running from 0.99 to 1.00.

Figure 8:

The top and bottom panels on the left hand side show the same variables as the top and bottom panels in Figure 7 (the wave energy fluxes are not shown). The panels on the right-hand side show the chromospheric ionization balance and FIP fractionation for selected elements. The bottom panel shows FIP fractionation for the abundance ratios S/O, He/O, Mg/O, Fe/O and Si/O, with the linestyles indicated as black lines, to be read on the left axis. One can see Fe/O and Mg/O fractionating to a value close to 4, Si/O to 2.6. S/O to 1.6 and He/O to 0.4. The ionization balance is shown as grey lines with the same linestyles for Fe, Mg, Si, S, and He. He stays neutral the longest, and matches calculations in Golding et al. (2014). Also shown are H and O as solid lines, labelled respectively. The O ionization balance follows that for H due to the strong coupling by charge exchange. The ionization balances for Fe, Mg, Si, and S are hard to distinguish on this plot, so the top right panel shows these in more detail, with the charge fraction scale running from 0.99 to 1.00.

Fe and Mg have similar charge state fractions for all altitudes of relevance, and hence fractionate to about the same degree. Si, although low FIP and 99.8% ionized in the region 1500 km to 2500 km, fractionates noticeably less. Around 1000 km altitude, Si is more highly ionized due to the increased flux in Ly α, which is now trapped by the increased opacity in the line. In the model presented here, no fractionation occurs at this height. S is also has a high charge state fraction, at 99.4%, but its ionization potential is higher than the energy of Ly α, and so it is not affected by the trapped radiation. This dependence on the ionization fraction comes from the form of ν_eff = ν _si ν _sn /(ξ _s ν _sn + (1 − ξ _s ) ν _si ) in the integrand of Eq. (22) where ν _si ≫ ν _sn , (Laming, 2004a), which is the case when the background gas is mainly ionized H. Only when ξ _s ≃ 1 to a high degree of precision does the second term in the denominator become negligible compared to the first, allowing strong fractionation to occur. Lower down in the chromosphere, where neutral H dominates, ν _sn ∼ ν _si , and this precise dependence on element charge state is lost.

Table 3 gives model fractionations for three different assumed coronal Alfvén wave amplitudes, 75, 95, and 110 km s⁻¹, which are initiated with amplitudes 0.6, 0.75, and 0.9 km s⁻¹ low in chromosphere A. Figures 7 and 8 correspond to the middle entry, 95 km s⁻¹. The model results are compared with observations taken from the literature; (a) Zurbuchen et al. (2002), given relative to O, (b) Bochsler (2007a), relative to O, (c) Giammanco et al. (2007, 2008), relative to H, (d) Bryans et al. (2009), given relative to the mean of O, Ne and Ar and, (e) Phillips et al. (2003), relative to H, (f) Ar, Sylwester et al. (2010a); K, Sylwester et al. (2010b); Cl, Sylwester et al. (2011); S, Sylwester et al. (2012); Si, Sylwester et al. (2013); and Na Phillips et al. (2010), all relative to H and given relative to the photospheric abundance of Asplund et al. (2009), and (g) SEP measurements from Reames (2014), given relative to O. Zurbuchen et al. (2002), Bochsler (2007a) and Giammanco et al. (2007, 2008) give abundances derived from in situ measurements in the slow solar wind. They generally agree best with model with coronal Alfvén wave amplitudes of 75–95 km s⁻¹. Bryans et al. (2009) give abundances derived from a deep SOHO/SUMER (Wilhelm et al., 1995, 1997) spectrum of the quiet solar corona, and are more consistent with a higher Alfvén wave amplitude, 110 km s⁻¹. The remaining references give abundance measured in solar flares with RESIK (Sylwester et al., 2005). All models assume a constant amplitude with height for slow-mode waves propagating up from the photosphere of 6.25 km s⁻¹. Fractionations are somewhat sensitive to this, in that increased slow wave wave amplitude decreases the degree of fractionation. However, for the case considered here, that of a coronal Alfvén wave on resonance with the coronal loop, most of the fractionation is restricted to a small region close to the top of the chromosphere where the slow-mode waves generated parametrically by the Alfvén wave driver are also significant. Rakowski and Laming (2012) extended such considerations to Alfvén waves away from the loop resonance. A similar FIP effect is produced, but the fractionation occurs over a wider layer of the chromosphere, as Alfvén waves penetrate deeper. Some subtle differences occur. S is more strongly fractionated in such a case, and He is depleted much less, both as a result of the difference in Alfvén wave behaviour. Slow-mode waves are also more strongly generated deeper in the chromosphere, and in cases such as this, their generation has a stronger effect on the fractionation. Laming (2004a) also considered the effect of different chromsopheric models from Vernazza et al. (1981). If VALC may be considered as a forerunner to the Avrett and Loeser (2008) model used here, and it does indeed give similar FIP fractionation, the result of Laming (2004a) in that stronger fractionations are found within cells at dark points (VALA, VALB) and weaker fractionation at network segments (VALD, VALE). However, these chromospheric models should probably be considered obsolete at the current time of writing.

Table 3: FIP Fractionations in Closed Magnetic Field (see text for details).

7.2 Open field

We next consider the FIP effect in open magnetic field. The chromospheric model is extrapolated upwards assuming a density scale height of 170000 km, to give a density profile comparable to that observed and modeled elsewhere (Laming, 2004b). The temperature is set at a maximum of 10⁶ K, but is similarly inconsequential as in the closed field case. Figure 9 shows the same panels as Figure 7, but extending to an altitude of 500 000 km. Five Alfvén waves are included, designed to match the spectrum given in Figure 3 of Cranmer et al. (2007), with amplitude in the transition region from their Figure 9. Waves of angular frequency 0.010, 0.031, 0.062, 0.093, and 0.124 s⁻¹ are included with amplitudes at 500 000 km of 12.5, 150, 75, 50, and 12.5 km s⁻¹, respectively. The integration of Eqs. (11) begins at 500000 km with outgoing waves only following Cranmer et al. (2007), and is taken back to the chromosphere. No account is taken of the motion of the coronal hole plasma. For the range of altitudes considered, the fast solar wind speed is always much less than the Alfvén speed, and is probably still insignificant compared to the uncertainty in the Alfvén speed.

Figure 9:

Solution for the coronal hole. The top panel shows δv and $\delta B/\sqrt {4\pi \rho}$ [Eqs. (12)], real components in black, imaginary components in grey. The middle panel shows the wave energy fluxes, left and right going, and their difference, divided by the magnetic flux density. Normalized thus, this difference should be constant in the absence of wave growth or damping, and provide a check on energy conservation in the integration. The bottom panel shows the ponderomotive acceleration, a.

Figure 10 shows a similar set of panels to Figure 8 above. Top left shows δv and $\delta {\bf{B}}/\sqrt {4\pi \rho}$ for the five waves in the chromosphere, with the real and imaginary parts distinguished as before. Bottom left now shows the chromospheric wave energy fluxes. Although we have made no assumption about where the waves originate, in the case of the coronal hole the usual interpretation is that Alfvén waves start out as kink mode waves on photospheric flux tubes, and propagate up into the coronal hole. This bottom left panel shows that most of the upgoing wave energy flux is reflected back down again, at the steep chromospheric density gradient. Of order 10% of the wave energy makes it out of the chromosphere, and more reflection occurs higher up (not included in our model). Higher frequency waves suffer less reflection than the low frequency waves.

Figure 10:

The top and bottom panels on the left hand side and the top panel on the right-hand side show the same variables as in Figure 9. Additionally, the amplitude of slow-mode wave generated parametrically by the Alfvén waves is also shown in the top right panel. Compared to the closed loop case with a wave on resonance, the ponderomotive acceleration has a stronger contribution lower down in the chromosphere. The bottom right-hand side panel shows the chromospheric ionization balance and FIP fractionation for selected elements. The bottom panel shows FIP fractionation for the abundance ratios He/O, Mg/O, and Fe/O, with the linestyles indicated as black lines, to be read on the left axis. The degree of fractionation is reduced from the closed field case. The ionization balance is shown as grey lines with the same linestyles for Fe, Mg, Si, S, and He, and is very similar to the previous, except that in the reduced radiation field of the coronal hole, He stays neutral longer.

The top right panel shows the ponderomotive acceleration. Superficially, it is very similar to the previous case, with a “spike” at the altitude where the chromospheric density gradient is steepest. However, the strong wave reflection leads to a stronger component of the ponderomotive acceleration at lower altitudes, around 1000 km above the photosphere, and a reduced acceleration associated with the “spike”. In principle, stronger fractionation can occur low down in the chromosphere because here the hydrogen is mainly neutral, whereas around the “spike” it is becoming ionized. This difference in the background H makes a big difference to the value of ν_eff in Eq. (22), and also to the resulting fractionation. The degree to which this actually happens is determined by the amplitude of slow-mode waves appearing in $v_s^2$ in the denominator of the integrand in Eq. (22). The model shown in Figure 10 assumes the same slow-mode wave amplitude as in the closed loop case, a constant value of 6.25 km s⁻¹, which when added in quadrature with the parametrically generated slow-mode wave amplitude eliminates the fractionation low down. Thus, the fractionation is restricted to the top of the chromosphere, and generally agrees well with coronal hole observations. Treating the Alfvén and acoustic waves in a more complete fashion (but only considering Fe/O), Cranmer et al. (2007) reach a similar result. The amplitude of acoustic waves developing low in the chromosphere in their model is higher than in ours, of order 10 km s⁻¹ from their Figure 9, though varying with altitude.

The effect of varying the slow-mode wave amplitude is illustrated in Table 4, where models are given for amplitudes of 5.85, 6.0, 6.05 and 6.25 km s⁻¹. Above about 6.25 km s⁻¹, the FIP fractionation slowly decreases with increasing slow-mode waves, assuming the Alfvén waves are kept constant. Below this value, the FIP fractionation increases dramatically. Observational ratios are taken from, (a) Zurbuchen et al. (2002), given relative to O, (b) Bochsler (2007a), relative to O, and (c) Ko et al. (2006), relative to H. FIP fractionations at the level of those in the first model column in Table 4, or higher, have been reported (Widing and Feldman, 1992; Young and Mason, 1997), and are always observed in open field structures. Other authors (Doschek and Laming, 2000; Del Zanna, 2003; Del Zanna et al., 2003) have not found large FIP effects in polar plumes. This last reference actually challenges the finding of Widing and Feldman (1992), (but not that of Young and Mason, 1997), arguing that an isothermal plasma at log T = 5.9 would produce the same Ne VI/Mg VI intensity ratio with photospheric abundances. Hence the reality, and certainly the ubiquity of strong FIP effects in polar plumes is questionable. Even so, the possibility of strong FIP effects in these structure is supported by our model, as Alfvén waves can have considerable amplitudes low in the chromosphere, and the sensitivity of our open field FIP model to the assumed slow-mode wave amplitude is perhaps realistic. We expect such sensitivity to be reduced in the case of torsional Alfvén waves, due to their different coupling to the slow mode (Vasheghani Farahani et al., 2011).

Table 4: FIP Fractionations in Open Magnetic Field (see text for details).

7.3 The helium abundance

The ponderomotive force was originally invoked to explain just the FIP effect (Laming, 2004a), i.e., the enhancement in coronal abundance of the low FIP ions. Once more accurate treatments involving the non-WKB analysis of Alfvén wave transport were implemented (Laming, 2009, 2012), it was noticed that as well as providing a satisfactory explanation of the FIP effect, the model also predicted a depletion of the He abundance, (and to a lesser extent Ne also) with respect to O in the corona and solar wind. As noted in Section 3, in the slow solar wind especially, the He/H ratio is reduced from its photospheric value and becomes more variable in slower speed slow solar wind. The He abundance is also depleted in the fast solar wind, but to a lesser extent, and is much less variable.

Rakowski and Laming (2012) investigated models for the depletion of He in more detail. They showed that similar behavior is seen in the ratio He/O measured by ACE/SWICS (see Figure 11 left panel); a depletion of He to about 0.4–0.8 of the solar photospheric value, with greater depletion seen the slower the solar wind speed, although the solar cycle dependence is not apparent in the time interval 1998–2011. Rakowski and Laming (2012) constructed models for a variety of loop lengths and corona magnetic fields, all using the Avrett and Loeser (2008) model chromosphere, and studied the fractionation produced as a function of the assumed Alfvén wave frequency with respect to the loop resonance frequency. For each case, the coronal wave amplitude was chosen to give a fractionation Fe/O by a factor of 4, as observed in the slow speed solar wind. As we have seen above, for waves that resonate with the coronal loop, most of this fractionation occurs at the top of the chromosphere, whereas off resonance, (or in open field regions) fractionation lower down in the chromosphere is possible.

Figure 11:

Left: He/O relative to the solar photospheric ratio as a function of the wave frequency, in units of the loop resonance frequency, for different loop lengths and magnetic fields. A trend of increasing He depletion with decreasing magnetic field strength, and possibly also increasing loop length, can be seen. Right: Wave energy transmission coefficients for the same loop models as a function of wave frequency. Shorter wavelengths (lower magnetic field, shorter loops) have broader resonances and are more easily transmitted the chromosphere-corona boundary. Images reproduced with permission from Rakowski and Laming (2012), copyright by AAS.

Results are shown in Figure 11 left panel. Helium is seen to be strongly depleted with respect to oxygen when the wave frequency coincides with the loop resonance. In these cases, the ponderomotive acceleration is restricted to the top of the chromosphere. This means that O can be accelerated into the corona once it becomes ionized, while He, the last element to remain neutral, is left behind. Elsewhere, where waves are not on resonance, the ponderomotive acceleration develops over a greater range of chromospheric altitudes. Correspondingly, the acceleration in the region where O is ionized is smaller, since we are restricting ourselves to cases where Fe/O fractionates to a factor of 4. Hence, O is not accelerated relative to He to the same extent, and the He/O ratio is unaffected, while otherwise the usual FIP effect still develops, albeit with subtle changes in the fractionation pattern.

Closer inspection of the left panel of Figure 11 also reveals greater depletion of He at the resonance with weaker magnetic fields. Again, the ponderomotive acceleration is becoming more concentrated towards the top of the chromosphere, but for a different reason. As the magnetic field weakens, the chromospheric layer where the plasma β = 1, the equipartition layer, moves to higher altitudes. At this layer, a myriad of wave phenomena occur; reflection, transmission and mode conversion, and we do not attempt to model this except to say that FIP fractionation must occur above this layer. Hence as this layer moves upwards, ponderomotive acceleration is more restricted to the upper chromospheric layers, and He/O becomes more depleted. This is most easily seen in Figure 11 for frequencies just above the resonant frequency.

In principle, the He/O depletion should also depend on loop length. Longer wavelength waves, resonating with longer loops, are more effectively reflected at density gradients. Thus, we would expect more He/O depletion to be associated with longer coronal loops, and this seems to be borne out by the three loop lengths with magnetic fields of 15 G. The three cases with 10 G coronal fields are less clear, mainly because for many wave frequencies, and Fe/O enhancement of 4 could not be achieved, and so these points are not plotted. The increased penetration of shorter wavelength waves into a density gradient before reflection is illustrated in the right panel of Figure 11. Wave energy transmission coefficients for the same loop models are plotted as a function of wave frequency. Waves with shorter wavelengths (lower magnetic field, shorter loops) have broader resonances and are more easily transmitted across the chromosphere-corona boundary.

The fact that lower values of He/O are to be found for longer loops and weaker magnetic fields may have some bearing on the origin of the slow speed solar wind, and more specifically the origin of its different speed components. Some authors (e.g., Cranmer et al., 2007) argue that both fast and slow speed solar wind originate in open magnetic flux tubes, and that the difference in fractionation arise from subtle differences in the wave propagation on such structures. We would argue here that different slow-mode wave amplitudes lower down in the chromosphere are the most likely variable. But in this case, the He depletion in fast and slow should be similar. Observationally, this is clearly not the case, and our inference that the He/O depletion is strongly dependent on the Alfvén wave frequency with respect to the loop resonance, being strongest when on resonance suggests that the slow solar wind plasma must originate in closed magnetic loops where it becomes fractionated, and that the Alfvén wave causing the fractionation must be generated in the loops themselves, in order that the loop resonant frequency is selected.

7.4 Significance of coronal Alfvén waves

The Alfvén wave levels suggested above are similar to those observed in solar flares (e.g., Alexander et al., 1998), but higher than those usually considered and observed in the solar corona (cf. Peter, 2001; De Pontieu et al., 2007; Peter, 2010; McIntosh et al., 2011). The predicted slow-mode wave amplitudes actually match quite well with the non-thermal broadening observed close to loop footpoints in an active region by Baker et al. (2013), and correlated with the locations of FIP fractionation (see Figure 3). The Alfvén wave values can be quite reasonable if the MHD fluctuation is confined to a small part of the coronal flux tube cross-section. In this case, a two component line profile should be expected, as in Peter (2001), with a narrow component with nonthermal line broadening with peak amplitude of ∼ 25 km s⁻¹, and a broad component corresponding to Alfvén waves with peak amplitude of ∼ 100 km s⁻¹. Depending on the filling factor of the strongly oscillatory plasma, this second component may or may not be readily detectable. Filamentary models of coronal and flare heating have been invoked to explain flare lightcurves (Warren and Doschek, 2005; Warren, 2006) and stellar coronal emission measure distributions (Cargill and Klimchuk, 2006). Figure 12 shows in the left panel the results of a 3D compressible MHD simulation including parallel heat conduction and radiation, of a coronal loop subject to forcing at its footpoints by photospheric motions (Dahlburg et al., 2012). The plane depicted is across the midpoint of the loop, and one can easily see localized temperature hotspots developing. Physically, the magnetic field is becoming stressed and periodically releasing the stored magnetic energy in small scale reconnection event. The right panel shows observations with the Hi-C instrument (Testa et al., 2013) of the footpoint region of a coronal loop. Filamented, and variable emission in Fe XII can be see, interpreted as the thermal conductive response to filamented and sporadic heating events higher up in the coronal portion of the loop. The left panel is scaled to 4000 km on a side, and so represents a similar spatial scale to that observed by Testa et al. (2013). The Fe XII emission peaks at a temperature of about 1.6 × 10⁶ K, just above the top of the temperature scale in the simulation. The filamentation appears on an angular scale of arseconds or smaller, and thus is only resolvable by Hi-C. Scales of this size would have been below the angular resolution of prior imaging spectrometers or imagers, and consequently any Alfvén waves associated with such structures would have been difficult to detect.

Figure 12:

Left: Results of a 3D MHD simulation. Temperature contours in the loop mid-plane are shown, illustrating the filamentary nature of the loop heating. The length scale is 4000 km on a side. The temperature scale runs from 4.9 × 10⁵ K to 1.3 × 10⁶ K. Image reproduced with permission from Dahlburg et al. (2012), copyright by ESO. Right: Observations of active region moss from Testa et al. (2013). Filamentary and variable emission is seen, most likely as a response to filamentary heating in the coronal portion of the loop, communicated to lower altitudes by heat conduction. At 1 arcsec ∼ 750 km, this structure is of comparable size to the simulation. Image reproduced with permission from Testa et al. (2013), copyright by AAS.

The filamentation is usually taken to derive from nanoflare heating (see below), though it could also refer to models of coronal heating by Alfvén resonance. In a flux tube with cross-B density gradient scale length l, a kink mode oscillation of the flux tube becomes Alfvénic at a resonant surface where the wave frequency ω = 2L/V _A , where L is the loop length and V _A is the Alfvén speed (see e.g., Ruderman and Roberts, 2002). The width of this resonant layer is δ ∼ (lν/ω) ^1/3, where ν = aV _A /R is the kinematic viscosity, a is the loop radius and R is the Reynolds number. The Alfvénic velocity fluctuations are larger than those of the kink mode by a factor l/δ = (l² R/a L)^1/3 ∼ 0.1R^1/3 under typical conditions. Such wave motions observed in the solar corona have been identified as kink (a subset of fast mode) mode waves (e.g., Nakariakov et al., 1999; Wang and Solanki, 2004). Alfvén waves which generate the ponderomotive force in the chromosphere have been much harder to detect (Van Doorsselaere et al., 2008), though see Erdélyi and Fedun (2007) and Tomczyk et al. (2007). The global kink modes above presumably derive from acoustic motions in the chromosphere driving loop footpoints initiating the loop oscillation, that then subsequently decay into Alfvén waves at the resonant surface. Turbulence associated with heating on particular field lines will only produce fractionation if chromospheric upflows are restricted to these field lines. However, if the upflow is the result of chromospheric evaporation, this is precisely what we should expect.

The nanoflare paradigm suggests that the dominant loop footpoint motions are of much lower frequency, and do not excite oscillations in the loop but act so as to build up magnetic stresses in the corona. These stresses periodically release themselves, in what has become known as a “nanoflare”, as a current sheet develops (Parker, 1988). Rappazzo et al. (2007, 2008) discuss the buildup of magnetic stresses within the framework of turbulence phenomenology, where it appears that velocity perturbations similar to the ∼ 30 km s⁻¹ observed should be expected. Longcope et al. (2009) conjecture that in impulsive reconnection in post-flare loops, only about 10% of the liberated magnetic energy is converted directly into heat, the rest reappearing as kinetic energy that ultimately drives turbulence. In the case of reconnection of field lines at angle θ, equating magnetic energy destroyed to kinetic energy gained, B² sin² (θ/2)/8π = ρυ²/2, suggests υ = υ _A sin θ/2. For B = 20 G and ρ = 1.67 × 10⁻²⁴ × 10⁹ g cm⁻³, υ _A = 1400 km s⁻¹, and υ = 100 km s⁻¹ implies θ = 8°, slightly larger than the expectation of Rappazzo and Parker (2013). Of course some magnetic energy may go directly to heat, but it is plausible that such wave generation explains why surveys to find localized hot plasma as evidence of nanoflare reconnection have generally been unsuccessful (e.g., Warren et al., 2011). Instead, energy goes from magnetic field to waves, and is thus gradually dissipated as heat throughout the corona, and not quickly and locally as might have been expected.

Sturrock (1999) gives a pedagogic review of the mechanisms by which various wave modes may be excited by reconnection. The reconnected field line is generally distorted, and this can either propagate away from the reconnection site as an Alfvén wave, or emit magnetoacoustic waves traveling perpendicularly to the magnetic field direction. Isobe et al. (2008) model small scale reconnection in the chromosphere. The emerging magnetic flux reconnects with the previously open field, to produce a reconnection jet accompanied by an upward propagating Alfvén wave, which appears to be of appropriate frequency (0.01 Hz) and amplitude (20 km s⁻¹ in the transition region) to give rise to some fractionation. Observational evidence of low-lying reconnection producing jets and transverse waves of similar frequencies and amplitudes has been reported (Nishizuka et al., 2008; He et al., 2009; Vasheghani Farahani et al., 2009). Kigure et al. (2010) explicitly consider the generation of Alfvén waves by magnetic reconnection, and find that a significant fraction of the magnetic energy released (several tens of %, depending on geometry and plasma β) can be carried off by Alfvén or magnetoacoustic (fast or slow mode) waves, with Alfvén waves dominating for β < 1. Liu et al. (2011a) and Liu et al. (2011b) discuss the role of temperature anisotropies and wave generation by the firehose instability in the outflow.

Van Ballegooijen et al. (2011) challenge some of these ideas and offer a more traditional view of an Alfvén wave heated corona, where Alfvén waves are introduced at loop footpoints from below and are either transmitted or reflected, following Hollweg (1984). They argue that “nanoflare” heating, as in Parker’s concept, cannot supply sufficient heat to the corona. However, the simulations of Dahlburg et al. (2012), (see also Gudiksen and Nordlund, 2004; Bingert and Peter, 2011), discussed above seem to contradict this statement. A million degree corona can indeed be heated and maintained by random motions of loop footpoints with timescale longer than the loop resonance. Further, Rakowski and Laming (2012) show that extended Alfvén wave propagation throughout the chromosphere, as in van Ballegooijen et al. (2011), is unlikely to correctly predict the depletion in the coronal abundance of helium.

7.5 Modeling the inverse FIP effect

One of the striking features of the Wood-Linsky relation illustrated in Figure 4 is how the coronal abundance anomaly smoothly changes from solar-like FIP bias at spectral types G to early K, to inverse FIP in M dwarfs. This suggests that a model for solar-like FIP fractionation should, with suitably chosen parameters, be capable of predicting an inverse FIP effect.

The model described above and in Laming (2004a, 2009, 2012) for the FIP effect suggests that Alfvén waves of amplitude approximately 100 km s⁻¹ are generated in the coronal loop at the resonant frequency, and remain trapped in the loop “resonant cavity”. Upon reflection from chromospheric footpoints, the waves develop a ponderomotive force in the steep density gradients there, and this force, acting on chromospheric ions (but not neutrals), preferentially accelerates these ions up into the corona. Laming (2012) studies the fractionations produced by waves on and off resonance, and Rakowski and Laming (2012) extend this to different loop lengths and magnetic fields, concentrating mainly on the fractionation of He with respect to O. These works only consider coronal Alfvén waves, with chromospheric acoustic waves included following Heggland et al. (2011) and Cranmer et al. (2007) as terms in the denominator of the integrand in Eq. (22). When these upcoming chromospheric acoustic waves are allowed to mode convert, at the layer where sound and Alfvén speeds are equal, to what in the magnetically dominated upper chromospheric become fast-mode waves, inverse FIP fractionation can result. This arises because the fast-mode waves undergo reflection back downwards as the Alfvén speed increases, giving rise to a downwards directed ponderomotive force than can compete with that due to the coronal Alfvén waves. Inverse FIP requires ∂δE²/∂z < 0. If waves propagate from chromosphere to corona (or from corona to chromosphere) without reflection, then ∂δE²/∂z > 0 always. This is because δE = δυB (where B is ambient field, assumed uniform here) and δυ increases as the density decreases. If waves propagating up from beneath are reflected back down again, δυ and δE must decrease with height, and ∂δE²/∂z < 0, giving rise to a downward ponderomotive force.

The process of mode conversion is shown schematically in the left panel of Figure 13, taken from Khomenko and Cally (2012). An upcoming acoustic (fast mode) wave where υ _A ≪ C _S (β ≫ 1) can be transmitted into the overlying region where υ _A ≫ C _S (β ≪ 1) as an acoustic (slow mode) wave, or mode converted to a magnetoacoustic (fast mode) wave. The magnetoacoustic wave refracts in the region where υ _A is increasing with height and eventually rejoins the lower β ≫ 1 plasma. The transmitted slow mode can continue propagating until it reaches an acoustic cut-off. When the plane in which the fast mode refracts is distinct from the plane of inclination of the magnetic field (indicated here by blue lines), it may also further mode convert to an Alfvén wave, which is not considered further in this paper. The acoustic waves have an energy transmission coefficient of (Cally and Goossens, 2008)

$$\matrix{{T = \exp \left({{{ - \pi \vert{\bf{k}}\vert\sec \theta \left({1 - {{(\sin \alpha \cos \phi \sin \theta + \cos \alpha \cos \theta)}^2}} \right)} \over {{{[{\rm{d(}}V_A^2/c_S^2{\rm{)/d}}z]}_{\beta = 1}}}}} \right)} \hfill \cr {\quad = \exp \left({ - \pi \vert{\bf{k}}\vert{H_D}\sec \theta \left({1 - {{(\sin \alpha \cos \phi \sin \theta + \cos \alpha \cos \theta)}^2}} \right)} \right)} \hfill \cr {\quad \;\; \rightarrow \exp (- \pi \vert{\bf{k}}\vert{H_D}\sec \theta {{\sin}^2}\theta),} \hfill \cr}$$

(30)

where α and θ are the angles to the vertical made by the magnetic field and the wavevector respectively, and ϕ is the polar angle between them. The last line gives the more familiar result in vertical magnetic field. The right panel of Figure 13 shows the acoustic to acoustic energy transmission coefficient for initially isotropic waves (in the upward going hemisphere) as a function of magnetic field inclination to the vertical (the angle α above), for values of ∣k∣ H _D = 0.25, 0.5, and 1. For solar oscillations with period 300 seconds, $k{H_D} = \sqrt {{\omega ^2}H_D^2/c_S^2 - 1/4} = 0.25$, where we have taken H _D = 168 km from Figure 6 and c _S = kT/m _p ≃ 6.3 km s⁻¹. In later type stars with deeper convection zones, we might expect kH _D to increase, since ω ∼ g/c _S increases with increasing g and decreasing c _S in the colder photospheres (see, e.g., Bruntt et al., 2010; Kjeldsen and Bedding, 2011), while H _D in the low chromosphere remains approximately constant, as far as can be determined from model chromospheres available in the literature (e.g., Fuhrmeister et al., 2005; Houdebine and Stempels, 1997; Vieytes et al., 2005). These factors would increase the degree of mode conversion in later type stars. Solar p-modes are also known to decrease in intensity and increase in width from solar minimum to maximum (Chaplin et al., 2000; Simoniello et al., 2010). This suggests that the trapping of acoustic modes within the solar envelope becomes less effective at solar maximum, and allows energy to leak out (Pinter et al., 2001). Sunspots have long been known to be sinks of p-mode energy (see Braun, 1995, and references therein), most likely through mode conversion or resonant absorption to Alfvén or fast-mode waves. P-modes are also known to decrease in intensity for later spectral types, modeled by Kjeldsen and Bedding (2011) as due to extra “leakage”.

Figure 13:

Left: Schematic diagram of acoustic to magnetosonic wave mode conversion at the plasma β = 1 layer of the chromosphere. An upcoming acoustic (fast-mode) wave where υ _A ≫ C _S (β ≫ 1) can be transmitted into the overlying region where υ _A ≪ C _S (β ≪ 1) as an acoustic (slow-mode) wave, or mode converted to a magnetoacoustic (fast-mode) wave. The magnetoacoustic wave refracts in the region where υ _A is increasing with height and eventually rejoins the lower β ≫ 1 plasma. The transmitted slow mode can continue propagating until it reaches an acoustic cut-off. When the plane in which the fast mode refracts is distinct from the plane of inclination of the magnetic field (indicated here by blue lines), it may also mode convert to an Alfvén wave, which is not considered further in this paper. Image reproduced with permission from Khomenko and Cally (2012), copyright by AAS. Right: Transmission coefficients for isotropic acoustic waves (in the upgoing hemisphere) as a function of the inclination of the magnetic field, for different values of kH _D , calculating by integrating a generalization of Eq. (30) in the region 0 ≤ θ ≤ π//2 and 0 ≤ ϕ ≤ 2π.

A further reason for the transition from FIP to inverse could be that in stars on the left-hand side of Figure 4, upcoming acoustic waves encounter an acoustic cut-off before reaching the β = 1 layer, and never have a chance to mode convert. In the stronger magnetic fields of later type stars, the β = 1 layer is deeper in the chromosphere, and upcoming acoustic waves will reach this first, before any acoustic cut off, and mode convert to fast-mode waves. The fast-mode waves are immune to the acoustic cut off, but ultimately refract back downwards.

We treat the fast-mode waves as approximately isotropic in the upward moving hemisphere, following Wood et al. (2012). Then the fraction reflected at chromospheric height z is

$${f_R}(z) \simeq \sqrt {1 - {{c_S^2({z_{\beta = 1}})} \over {V_A^2(z) + c_S^2(z)}}}$$

(31)

where z_{β = 1} is the chromospheric height where mode conversion occurs. The ponderomotive acceleration due to fast-mode waves is then

$$a = {{{c^2}} \over 4}{\partial \over {\partial z}}\left({{{\delta {E^2}} \over {{B^2}}}} \right) = {{\delta {v^2}} \over 2}(1 - {f_R}){1 \over {\delta v}}{{\partial \delta v} \over {\partial z}} - {{\delta {v^2}} \over 4}{{\partial {f_R}} \over {\partial z}}.$$

(32)

The two terms represent an upwards contribution arising as the fast-mode waves increase in amplitude as they propagate through lower density plasma, and the downwards contribution arising from fast-mode wave reflection. Evaluating

$${{\partial {f_R}} \over {\partial z}} = {{c_S^2({z_{\beta = 1}}){V_A}} \over {{{(V_A^2 + c_S^2)}^2}{f_R}}}{{\partial {V_A}} \over {\partial z}} = {{c_S^2({z_{\beta = 1}})V_{_A}^2} \over {{{(V_A^2 + c_S^2)}^2}{f_R}}}\left({{1 \over {{H_B}}} - {1 \over {2{H_D}}}} \right)$$

(33)

and assuming from the WKB approximation

$${1 \over {\delta v}}{{\partial \delta v} \over {\partial z}} = {{ - 1} \over {2{H_B}}} - {1 \over {4{H_D}}},$$

(34)

where H _D and H _B are the signed density and magnetic field scale heights, we find from Eq. (32)

$$a = {{\delta {v^2}} \over {{f_R}}}\left\{ {({f_R} - 1)\left({ - {1 \over {8{H_D}}} - {1 \over {4{H_B}}}} \right) + {{c_S^2({z_{\beta = 1}})} \over {{{(V_A^2 + c_S^2)}^2}}}\left({ - {{c_S^2} \over {8{H_D}}} - {{c_S^2} \over {4{H_D}}} - {{V_A^2} \over {2{H_D}}}} \right)} \right\}.$$

(35)

Remembering that both H _D and H _B are negative, and f _R < 1, the first term in curly brackets is negative, giving rise to Inverse FIP effect, and the second term is positive, giving the more usual FIP effect. In conditions where V _A ≫ c _S , an overall downwards pointed ponderomotive acceleration requires ∣H _D ∣ < ∣H _B ∣/6 in this simple model.

Additional reflection of fast-mode wave from, e.g., density fluctuations (not included in this model) would relax the requirement. So too would fast-mode waves spreading out laterally from a horizontally localized source. Even so, Eq. (35) implies that inverse FIP effect is more likely to found in stars with minimal magnetic field expansion through the chromosphere, which fits with its observation in M dwarfs. While the magnetic fields measured in these stars are similar to those in the Sun, the filling factor is higher (e.g., Donati and Landstreet, 2009; Reiners et al., 2009), allowing less volume for expansion with increasing altitude.

Figure 14 illustrates a calculation designed to give an inverse FIP effect. The model is similar to that shown in Figure 3 of Laming (2012). A loop of length 100 000 km, with a 80 G magnetic field is considered, with a resonant Alfvén wave of frequency 0.28 rad s⁻¹. The magnetic field is compressed by a factor 0.5 through the chromosphere (previously it was 0.2), and a fast-mode wave amplitude of 10 km s⁻¹ is included at the β = 1 layer, which is allowed to propagate and refract as described above. The model chromosphere derives from Avrett and Loeser (2008), though future work should implement a model stellar chromosphere. The top left panel shows the variation of the perturbations δυ and $\delta B/\sqrt {4\pi \rho}$ associated with the coronal Alfvén wave, and the bottom right panel shows the Alfvén wave energy fluxes, both upward and downwards directed. The dotted line in the bottom right panel shows the difference in wave energy fluxes. The top right panel shows the ponderomotive acceleration. The positive contribution in the upper chromosphere (solid curve) comes from the coronal Alfvén waves. The negative contribution lower down (dashed curve) comes from the total internal reflection of fast-mode waves. The dotted curve gives the amplitude of acoustic waves through the chromosphere, modeled as outlined above. The bottom right panel gives the FIP fractionations for the ratios S/O, He/O, Mg/O and Fe/O. He/O remains unchanged, but all others display an inverse FIP effect, coming from the fast-mode waves. The positive FIP that would arise from the Alfvén waves higher in the chromosphere is suppressed by the upward flow speed through the chromosphere, taken here to be 10⁶ cm s⁻¹ at a chromospheric density of 10¹⁰ cm⁻³, and of course smaller lower down in the chromosphere due to the increased density. This upflow is now included in the Alfvén wave transport equation (11). Upflows of at least this speed are typical of the gradual phase of solar flares (e.g., Czaykowska et al., 1999). High in the chromosphere, the He ionization fraction is increased relative to the earlier examples by the choice of an “active region” spectrum from Vernazza and Reeves (1978) with which to illuminate the chromosphere. This will reduce any depletion of He that might otherwise occur in conditions giving rise to positive FIP effect, and might be relevant to the relatively high He abundances observed in flares and CMEs (e.g., Feldman et al., 2005; Wimmer-Schweingruber et al., 2006).

Figure 14:

Illustration of a model demonstrating the origin of the Inverse FIP Effect. The top left panel shows the variables δυ and $\delta B/\sqrt {4\pi \rho}$ for the coronal Alfvén wave. The bottom left panel shows the upgoing (dashed curve) and downgoing (solid curve) wave energy fluxes. The dotted line shows their difference. The top right panel shows the ponderomotive acceleration. The positive contribution in the upper chromosphere (solid curve) comes from the coronal Alfvén waves. The negative contribution lower down (dashed curve) comes from the total internal reflection of fast-mode waves. The positive fractionation induced by the Alfvén waves is suppressed by the choice of evaporative flow speed, which is higher in the lower density regions of the chromosphere due to continuity. Suppression of fractionation low in the chromosphere by slow-mode waves is reduced in this example, because the slow modes mode convert to fast modes. The dotted curve gives the amplitude of acoustic waves through the chromosphere. The bottom right panel gives the FIP fractionations for the ratios S/O, He/O, Mg/O and Fe/O. He/O remains unchanged, but all others display an inverse FIP effect. The choice of an “active region” spectrum from Vernazza and Reeves (1978) has increased the ionization fraction of He, compared to the earlier examples.

The transition from FIP effect to inverse FIP effect with increasing fast-mode wave amplitude at the β = 1 layer is illustrated in Table 5. Models with fast modewave amplitudes of 5, 10, and 15 km s⁻¹ are compared with abundances in M dwarfs taken from Liefke et al. (2008), who compare observed coronal abundances with solar photospheric abundances of Asplund et al. (2005a). The coronal abundances for EV Lac given by Laming (2009) are in better agreement with the models, especially for Ne/O and S/O, but even so, it is clear that the broad systematics of the inverse FIP effect are well reproduced by the models in Table 5. Results for further minor ions observed in σ Gem and HR 1099 are taken from Huenemoerder et al. (2013a,b). The Alfvén wave amplitude has been reduced from that in Figure 7 by a factor of four to six. Wood and Laming (2013) argue that this might be appropriate in the strong magnetic fields of late type stellar coronae: Drake et al. (2006) studied the efficiency of electron acceleration in reconnection with the ambient plasma β (the electron plasma β _e = 8σn _e k_BT _e /B², to be more precise). They found maximum energy input to electrons at β _e = 0, with reduced electron heating at higher β _e , or lower magnetic field. We suggest that at the left-hand side of the Wood-Linsky relation, coronal reconnection primarily generates Alfvén waves that end up causing positive FIP fractionation when they reflect from the chromosphere. As one moves to the right, to later spectral type, coronal reconnection puts more energy into electrons, and less into waves. Consequently, the positive FIP effect diminishes.

Table 5: FIP and Inverse FIP Effects

While inevitably a highly simplified model of chromospheric wave processes, we take the potential for the ponderomotive force to explain the Inverse FIP effect at later spectral types, as well as the more usual FIP effect in the Sun, as a significant point in its favor. The Inverse FIP effect is also observed in many other more active stars, and we expect a similar explanation to hold there. However, the wave origin will be more complicated when additional processes due to stellar rotation, tidal interaction (e.g., RS CVn binaries) and accretion (e.g., T Tauri stars) are included.

7.6 Saturation

We conclude this section with a simple discussion of what might limit the absolute magnitude of the FIP fractionation. Alfvén waves of arbitrarily high amplitude will eventually erase the density gradients that give rise to the ponderomotive force. We estimate the ponderomotive acceleration at which this will occur, and hence a limit on how high this acceleration can go, as follows.

The density in a gravitationally stratified atmosphere with a ponderomotive acceleration is

$$\rho = {P \over {v_s^2}}\exp \left({ - gz/v_s^2 + 2\int \xi a{\nu _{{\rm{eff}}}}/{\nu _s}/\nu _s^2{\rm{d}}z} \right),$$

(36)

where all symbols are defined above in Section 6.5, and here the element s of interest is H. Then

$${1 \over {{H_D}}} = {{\partial \ln \rho} \over {\partial z}} = - 2{{\partial \ln {v_s}} \over {\partial z}} - {g \over {v_s^2}} + {{2gz} \over {v_s^2}}{{\partial \ln {v_s}} \over {\partial z}} + 2\xi a{{{\nu _{{\rm{eff}}}}} \over {{\nu _s}v_s^2}}.$$

(37)

We substitute a = −δυ²/8H _D to find

$${1 \over {{H_D}}}\left({1 + {\xi \over 4}{{{\nu _{{\rm{eff}}}}} \over {{\nu _s}}}{{\delta {v^2}} \over {v_s^2}}} \right) = - 2{{\partial \ln {v_s}} \over {\partial z}}\left({1 - {{gz} \over {v_s^2}}} \right) - {g \over {v_s^2}} = {1 \over {{H_{D0}}}},$$

(38)

where H _{D 0} is the density scale length when a = 0, i.e., in the absence of the ponderomotive acceleration. Consequently,

$$a = {{{a_0}} \over {1 + {\textstyle{\xi \over 4}}{\textstyle{{{\nu _{{\rm{eff}}}}} \over {{\nu _s}}}}{\textstyle{{\delta {v^2}} \over {v_s^2}}}}} = {\left({{1 \over {{a_0}}} - {{{H_{D0}}} \over {v_s^2}}{1 \over {1 + (1/\xi - 1){\nu _{si}}/{\nu _{sn}}}}} \right)^{ - 1}},$$

(39)

where a₀ = −δυ²/8H _{D 0}, the ponderomotive acceleration in the unmodified density gradient. Hence, as ${a_0} \to \infty,\;a \to - (1 + (1/\xi - 1){\nu _{si}}/\nu)v_s^2/{H_{D0}}$ which is in general comparable to the ponderomotive accelerations invoked in this paper to explain the FIP effect, if we take ξ = 1, with υ _s ∼ 10⁶ cm s⁻¹ and H _{D 0} ∼ 10⁶ cm. A small departure from full ionization (ξ < 1 increases this estimate quite quickly, because ν _si ≫ ν _sn . In this case, we would have to appeal to properties of the Alfvén waves themselves to explain the relative constancy of the FIP effect. If the waves are restricted to filamentary sections of a coronal loop, and are not monolithic oscillations of the whole loop itself, then regions of velocity shear will exist between oscillating and non-oscillating regions of the loop. This velocity may be expected to excite further wave motions, for example drift waves, which could provide another means of saturating the ponderomotive acceleration. Further developments along these lines are beyond the scope of this review.

8 Conclusions & Future Work

In this review, we have attempted to show how the interpretation of abundance enhancements or depletions arising due to the action of the ponderomotive force due to various MHD waves offers the potential of a rather complete description of the phenomenon. It may also be hoped that advances along these lines, together with the detection and observation of waves in the solar atmosphere will be a profitable route towards solving the problem of coronal heating. Here, we highlight some of the weak spots in the model, and areas where extra effort might provide a significant advance.

• 1. Coronal Waves: Concentrating first on the solar FIP effect, our models above give a good account of the observed abundance anomaly with a coronal Alfvén wave amplitude of around 100 km s⁻¹. This is a peak wave amplitude, and should therefore be expected to give rise to a nonthermal line broadening around 70 km s⁻¹, measured at half maximum line intensity. This is higher than usually observed, but is not necessarily a problem if the line width is “diluted” by the filamentary structure across the loop. One important question is then to understand quantitatively where this velocity amplitude originates. We have sketched out some possibilities above, nanoflare associated reconnection and Alfvén resonance, but this is an area where numerical simulation (e.g., Dahlburg et al., 2012) should be expected to yield new insights. The amplitude of waves generated will probably depend on the values of the coronal resistivity and viscosity, and thus have implications for theories of coronal heating. Different mechanisms of coronal heating might also be expected to produce Alfvén waves of different polarizations. The examples given in this review have treated shear Alfvén waves, such as might be expected to derive from reconnection. Alfvén waves resulting from resonant absorption would be torsional waves, and those generated by a reconnection outflow by a firehose instability would exhibit some circular polarization. The Alfvén wave transport equations and fractionation (Sections 6.4 and 6.5) do not change with polarization, but the coupling to other wave modes (Section 6.6) does. Pure parallel propagating circularly polarized waves do not couple to slow modes at all, while the case of torsional waves has been considered by Vasheghani Farahani et al. (2011). On twisted flux tubes, pure torsional Alfvén waves do not exist, and some degree of mixing with the compressional kink mode is inevitable. It remains to be seen whether these changes in the wave physics will result in detectable changes in FIP fractionation, and if so, whether this represents a new avenue of approach to the problem of coronal heating.

• 2. Chromospheric Waves: The solar FIP effect is subtly different depending on the altitude in the chromosphere where the fractionation occurs. High in the chromosphere, where H is becoming ionized, Fe and Mg fractionate more than Si, and S behaves more like a high FIP element. He can also be depleted relative to O. In the lower chromosphere where H is neutral, the low FIPs fractionate to essentially the same degree, and S behaves more like a low FIP element. He/O remains unchanged. Such fractionation can occur with off-resonant Alfvén waves, e.g., in an open field region, or with upcoming fast-mode waves in sufficiently diverging magnetic field. An important goal for spectroscopic and in-situ observations should be to obtain data of sufficient quality to distinguish between these two possibilities. Possibly the best extant spectroscopic analysis, that of quiet solar corona by Bryans et al. (2009) (given as column “d” in Table 3) strongly favors fractionation at the top of the chromosphere.

  Measurements of the S abundance made in situ in the slow speed solar wind often show significantly higher values than those obtained from spectroscopy (e.g., Giammanco et al., 2007; Reisenfeld et al., 2007). The comparison between these two forms of measurement is very clear in Figure 1 of Schmelz et al. (2012). Another element predicted to behave similarly (Rakowski and Laming, 2012) is C. Unfortunately, spectroscopic measurements of the C abundance in the solar corona are very difficult, because at coronal temperatures, C is typically fully ionized and emits no lines.

  Fractionation low down in the chromosphere can occur with Alfvén waves well away from the loop resonant frequency, such that they are not trapped in the coronal loop, or with upward propagating fast-mode waves in region where the magnetic field expands, giving rise to positive FIP fractionation from Eq. (35). He is well known to be present with high abundance in CMEs (Wimmer-Schweingruber et al., 2006), consistent with fractionation low in the chromosphere, but S, the other element crucial in this regard is typically not measured. Whether fractionation occurs low down or high up depends not only on the coronal Alfvén wave, but also on wave physics in the chromosphere. The mode conversion acoustic waves to fast-mode waves at the β = 1 layer makes a connection with the fields of helioseismology and asteroseismology. There is much observational and theoretical work ongoing on these aspect of chromospheric wave propagation that is relevant to the FIP effect. One key component to this will be chromospheric vector magnetic fields. Currently, chromospheric and coronal magnetic fields are extrapolated from photospheric magnetic field observations. Uncertain knowledge of the magnetic field expansion through the chromosphere makes it difficult to know where mode conversion occurs, and whether upcoming fast-mode waves should give FIP or inverse FIP effects.

  Considerable interest has arisen recently in the idea that the solar corona and wind might be supplied by Type II spicules accelerated directly from the chromosphere (e.g., De Pontieu et al., 2011; Martínez-Sykora et al., 2011), rather than plasma being evaporated into a coronal loop before being released into the solar wind. We comment here that in such a case, it is difficult to see how a FIP effect could arise. With reference to Eq. (22), the flow velocity associated with the spicule motion is likely to increase $v_s^2$ in the denominator of the integrand to an extent such that the integral tends to zero, and ρ _s (z _u ) = ρ _s (z _l ), yielding no fractionation. In simulations, Martínez-Sykora et al. (2011) find Type II spicule material extending to temperatures close to 10⁶ K, but no higher, consistent with the temperature range over which Laming et al. (1995) observed photospheric abundances (see Figure 1). Discontinuities in several other observables have been located between 500 000 K and 10⁶ K in the solar atmosphere (Feldman, 1983, 1987), and further considerations of element abundances (Feldman, 1998a) reinforce the conclusion of Laming et al. (1995). Other authors have also questioned the connection between coronal mass supply and Type II spicules on the basis of spectral line profiles (Patsourakos et al., 2014; Klimchuk and Bradshaw, 2014). Goodman (2014) argues on energetics grounds that Type II spicules may power the quiet solar corona and coronal holes, but not active regions.

  Type II spicules are most likely the cause of the absence of the FIP effect at temperatures below about 10⁶ K. However, in the case of Procyon, with its lower surface gravity, Type II spicules are possibly the most likely reason why its corona appears to have photospheric composition, unlike the other F dwarfs of similar spectral type in Figure 4. It is interesting to note that Drake et al. (1995a), without knowing the cause, recognized that the FIP effect appeared in the full-disk solar spectrum at about the temperature where the supergranulation disappeared from solar images, and speculated that if a similar transition happened on Procyon, it would occur at higher temperature.

• 3. Solar Observations: Detailed spectroscopy and in situ measurements should aim to distinguish between the two regimes of FIP fractionation mentioned above, i.e., low or high in the chromosphere. The aim should be to try and measure several element abundances simultaneously, not just the evaluation of one or two abundance ratios. This will ultimately require spectrometers with bandpasses specially designed for the purposes. The Hinode/EIS instrument, for example, was designed in the 1990s (well before the ponderomotive force model of the FIP effect was published) to maximize the coverage of lines from Fe ions, and so has rather few lines from high FIP ions within its bandpass, S being the most prominent. However, Hinode/EIS does offer imaging spectroscopy sensitive to the FIP effect, as demonstrated by Baker et al. (2013). The observation of FIP enhanced regions correlated with high non-thermal broadening at loop footpoints is an important advance. The filamentary coronal heating, and correspondingly filamentary FIP fractionation could be potentially observable as a variation in FIP effect across the cross section of a coronal loop. Increased efforts to measure absolute abundances (i.e., relative to H) would also yield insights into other mechanisms working to modify element abundances, and be advantageous in comparisons of abundances from remotely sensed spectroscopic observations with those measured in situ in the solar wind.

• 4. Stellar Observations: The quality of stellar observations is possibly less likely to improve in the future than those of solar observations, since missions in X-ray astronomy are fewer and further spaced in time than solar missions. Imaging spectroscopy is of course not possible, so the same comments about detailed spectroscopy to measure as many element abundances simultaneously apply. The main advance here will come from measuring abundances in a wider range of stellar targets. Observing more F dwarfs would flesh out the bottom left hand corner of Figure 4 and really establish a saturation of the FIP effect at about the level observed in the Sun, and no higher. This would then be interpreted as the FIP effect established solely by coronal Alfvén waves, with no contribution from upcoming fast modes. Further observation with Chandra of τ Bootis A would establish whether contamination from its M dwarf companion is responsible for its anomalous inverse FIP effect, or whether this is intrinsic to the F dwarf, and presumably due to the close-in Jupiter mass planet.

  Observations of inverse FIP effect exist in many more active and exotic stellar targets than those plotted in Figure 4. We have somewhat neglected discussion of these, for the simple reason that in trying to reach theoretical understanding of where the Inverse FIP effect comes from, it is obviously advantageous to start with simple objects first, before moving onto more complicated ones. Strong inverse FIP seen in RSCVn binaries with tidal interaction would suggest that the planet hosted by τ Boo A might produce the same effect. However, ε Eridani also hosts a Jupiter mass planet, apparently with no unusual coronal abundance effects. While on the subject of stellar “complexity”, we note the poor state of knowledge of M dwarf chromospheres and photospheric abundances. This is an intrinsic issue, due to the complicated stellar spectra with many molecular bands and otherwise unidentified lines. There appears to be no “magic bullet” in sight, other than detailed careful work on obtaining and modeling such data. Further knowledge of asteroseismology and associated wave physics may be expected to come from the Kepler mission (Koch et al., 2010).